地鐵車輛輔助變流器的氣動噪聲研究

2019-01-31 02:49:24劉海濤趙清良王永勝

西南交通大學學報 2019年1期

丁杰，張平，劉海濤，李華，趙清良，王永勝

（1. 湘潭大學土木工程與力學學院，湖南湘潭 411105；2. 株洲中車時代電氣股份有限公司技術中心，湖南株洲412001）

隨著乘客舒適性要求的提高，地鐵車輛的設備氣動噪聲需要嚴格控制. 輔助變流器作為地鐵車輛的重要設備，由柜體、變流器模塊、變壓器、風機和流道等部件組成，安裝于車廂底部，四周無裙板遮擋，自身產生的氣動噪聲會直接輻射到車外乘客，也會以繞射、透射等方式傳播到車內乘客，有必要對其進行控制.

研究人員關注地鐵車輛的設備噪聲. 張曉排等[1]通過測量地鐵車輛在靜止情況的車內噪聲發現，車輛的設備噪聲影響較大. 薛紅艷等[2]采用噪聲與振動測試分析系統對車內噪聲進行測試得知，車內噪聲主要為輪軌噪聲和設備噪聲，近車頂處噪聲主要來自空調機組機械振動產生的噪聲和送風口氣動噪聲. 任海等[3]分析了地鐵車輛運行時車內噪聲的成因、傳播途徑，并針對噪聲源、隔聲、減振和吸聲等多方面提出控制措施. 變流器作為地鐵車輛的重要設備，對車內外噪聲影響的研究尚未找到，僅找到研究自身噪聲大小、分布情況和簡單降噪處理的文獻[4-5]. 隨著計算機發展和氣動噪聲數值仿真方法日趨完善，利用數值仿真手段預測和控制變流器氣動噪聲成為可能. 遺憾的是，尚未有變流器數值仿真的相關文獻，只能借鑒與之相類似的文獻，如空調系統等. 李啟良等[6]搭建了風機、風道的氣動噪聲仿真模型，基于臺架試驗結果建立了空調系統氣動噪聲數值仿真方法. 風機是變流器、空調系統等設備的主要噪聲源. 預測和控制風機噪聲能有效解決變流器等設備的氣動噪聲問題. 在風機氣動噪聲預測方面，Lee等[7]計算了某空調用離心風機葉片通過頻率噪聲，首先從非定常流場中提取聲源信息，然后結合邊界元方法計算其噪聲. Broatch等[8]采用渦分離模型對某離心壓縮機的壓力脈動和氣動噪聲進行仿真研究，考慮了風機殼體的影響，并預測到出口管道內部的嘯叫聲. 優化葉型和改善進入來流均勻性是降低風機噪聲的主要途徑. 左曙光等[9]研究了風機葉片彎角、數目、葉輪與隔板的徑向間隙，明確葉輪與隔板的徑向間隙對風機遠場噪聲的影響最大. 劉曉良等[10]研究了串列葉片不同葉片相對長度和不同葉片相對周向位置對風機氣動噪聲的影響. 葉學民等[11]通過數值仿真發現逆流向斜槽、雙斜槽、上階梯葉頂和下階梯葉頂均可有效提高風機性能，葉頂形狀改進后聲壓級隨頻率增大發生小幅提高，頻譜形態發生明顯改變. 王樹立[12]通過改善離心風機進口速度均勻性實現噪聲降低2.2 dB（A）.

綜合以上文獻調研可知，有必要建立變流器氣動噪聲源和傳播過程的數值仿真方法，并借鑒以往噪聲控制手段來實現變流器噪聲的控制. 為此，本文以存在噪聲超標問題的某地鐵車輛輔助變流器為對象，通過數值仿真和試驗相結合方法進行氣動噪聲研究，比較兩者結果差異，尋找噪聲超標原因并施加相應控制措施，為變流器開發提供參考.

1 聲類比理論與氣動噪聲計算流程

1.1 理論基礎

旋轉機械類噪聲主要為渦流產生的氣動噪聲，通常采用聲類比方法進行計算. 該方法基于Lighthill法[13-14]，并結合Curle理論[15]，具體如下：

（1） Curle方程的體積分作為有限元區域的體源；

（2） Curle方程的面積分作為邊界條件；

（3）自由場的格林函數作為其它邊界條件.

通過連續性方程和動量方程簡化得到Lighthill聲類比方程為

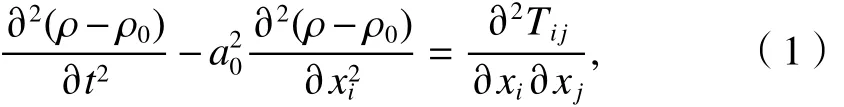
式中：t為時間；ρ為流場當地的流體密度；ρ0為流體參考密度；a0為聲速；xi、xj表示不同方向的坐標；Tij為Lighthill應力.

在計算域Ω上積分，并乘以測試函數 δρ ，可得

式中：δ為迪拉克函數.

應用分部積分產生弱變分形式為

式中：ni為物體表面的單位外法向矢量在i方向上的分量；Γ為計算域的邊界.

面積分上應用應力為

式中：總應力 Aij= ρvivj+(p-p0)δij-τij；p0為(參考壓力；p為流場當地壓力；粘性應力， μ 為流體動力粘度；克羅內克符號; xk為 k 方向坐標；vi、vj和 vk分別為i、j和k方向的流體速度分量.

式（4）可以表示為

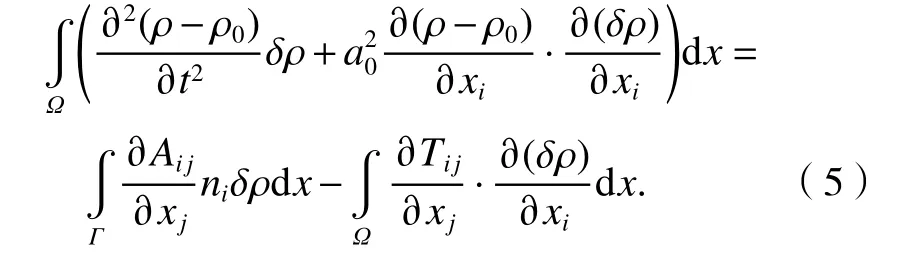
1.2 計算流程

根據式（1）～（5），輔助變流器氣動噪聲可采用流場和聲學耦合的方法計算. 圖1為輔助變流器氣動噪聲計算流程. 首先利用Pro/E等軟件建立輔助變流器三維CAD模型；然后利用ICEM-CFD軟件分別劃分計算流體力學（computational fluid dynamics，CFD）網格和聲學網格；再利用Fluent軟件對CFD網格進行穩態和瞬態流場計算，獲得輔助變流器的氣動噪聲源特性；接著進行ICFD （inverse CFD）轉換，將速度和密度時域量快速傅立葉變換（fast Fourier transform，FFT），變換為頻域結果，插值映射到聲學網格上；最后進行聲學計算，通過聲類比法得到聲源在流道和外場的聲傳播特性.

圖1 輔助變流器氣動噪聲計算流程Fig.1 Calculation flowchart for aerodynamic noise in auxiliary converter

2 模型與仿真方法

2.1 仿真對象

圖2為某地鐵車輛輔助變流器結構布局和冷卻風流向示意圖. 輔助變流器柜體骨架由鈑金件組焊而成，外部均為板結構. 離心風機安裝在輔助變流器柜體內，主要由支撐部件、電機和葉輪組成，其中風機葉輪包含6個徑向后彎葉片，運行過程中通過電機直接驅動. 冷卻空氣在風機的抽吸下由柜體頂部的2個進風口進入流道，依次冷卻變流器模塊、電抗器和變壓器等，最后由出風口吹出. 進出風口布置有濾網，進風口和柜體中面積較大的板上粘貼了吸聲材料.

圖2 結構布置和冷卻風流向示意Fig.2 Schematic diagrams of structure layout and cooling air flow

2.2 網格劃分

基于Pro/E軟件建立的輔助變流器三維CAD模型中，各零部件包含了豐富的細節特征，比如加強筋、支座、板邊、布線管、螺栓等. 這些流道的突出物雖然會對氣流產生擾動，但由于流道氣流速度較低（2 m/s以下），自身產生的噪聲影響不大. 在本次建模中對這些突出物予以簡化. 簡化原則主要有：（1）提取與空氣流動和氣動噪聲傳播相關的幾何模型，如濾網、流道、風機、變流器模塊散熱器、電抗器、變壓器和部分柜體結構等；（2）刪除對氣流擾動和噪聲傳播影響較小的部件，如螺栓、支座等；（3）進出風口的濾網通過設置合適阻尼參數的多孔介質材料進行等效.

輔助變流器內部流道復雜，利用ICEM-CFD軟件采用四面體網格和六面體網格相結合的網格劃分方法. 風機是輔助變流器氣動噪聲主要噪聲源，需要劃分精細且合理的六面體網格，在保證風機區域網格質量的同時，為了更好地滿足大渦模擬（LES）要求，風機壁面首層網格質心到壁面的無量綱距離約為3. 輔助變流器流道壁面劃分三角形網格，網格尺寸大多集中在3～10 mm，得到的面網格和體網格數分別為400萬和1 100萬. 風機區域的結構化體網格如圖3所示，整個計算域的CFD網格如圖4所示.

圖3 風機區域的體網格Fig.3 Volume mesh of fan region

圖4 輔助變流器計算域的CFD網格Fig.4 CFD mesh of computational domain for auxiliary converter

聲學計算所需的網格尺寸由計算頻率決定. 風機葉片數為6，轉速為2 900 r/min，可知基頻為290 Hz.風機在基頻處會產生明顯噪聲峰值，且風機噪聲往往呈現明顯的倍頻效應，因此噪聲計算需覆蓋5倍基頻，即分析到1 500～2 000 Hz左右. 根據聲學網格需要保證每波長6～8個網格的原則，計算得到聲學網格尺寸不超過28.3 mm（每波長取6個網格），即可滿足2 000 Hz計算要求. 基于上述原則，利用ICEM-CFD軟件得到如圖5所示的聲學網格. 為了有效體現輔助變流器進風口和流道內部多處的吸聲材料，在吸聲材料所在位置定義為與吸聲系數相對應的導納邊界.

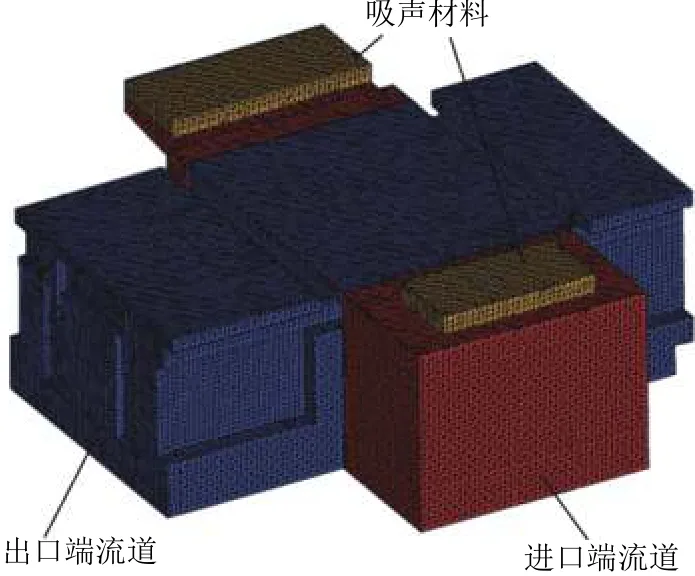
圖5 輔助變流器聲學網格Fig.5 Acoustic mesh of auxiliary converter

輔助變流器外部還需要參照噪聲試驗的條件建立聲傳播區域，為簡化起見，設置一個包圍輔助變流器柜體的立方體區域，區域的底面距離柜體底部1.05 m，設置為全反射的剛性壁面，區域的其余5個面均距離柜體表面1 m，設置為表征無反射邊界的無限元邊界，并針對該區域劃分體網格.

2.3 仿真計算方法

采用基于有限體積法的Fluent軟件進行輔助變流器氣動噪聲源計算時，為提高計算過程的收斂性，首先進行穩態計算，得到流場時均量，分析風機、流道內的速度、壓力和流線分布特征，然后將穩態計算結果作為瞬態計算的初始場，最后進行瞬態計算. 穩態計算采用雷諾時均方程的RNG湍流模型，并結合非平衡壁面函數[16]，瞬態計算采用大渦模擬的S-L亞格子模型[17]. 考慮流體可壓縮性，密度通過理想氣體狀態方程計算得到. 按照輔助變流器內部動靜關系，將計算域分成進出風口區域和風機區域. 不同區域之間通過滑移網格交界面進行信息傳遞. 進出風口邊界條件設置為壓力邊界，在固壁處采用無滑移邊界條件. 壓力和速度的耦合求解采用SIMPLE算法，壓力項離散采用標準差分格式，動量項采用邊界中心差分格式，時間采用二階隱式格式. 仿真計算時間步長取葉片轉過2° 對應的時間，即1.149 ×10-4s，其截止頻率為4 350 Hz，滿足風機試驗結果中所關注的頻率范圍. 每個時間步長迭代15次，以保證每個時間步長的計算收斂. 仿真過程中，風機瞬態計算進入第3圈后，監控量呈周期性波動，因此從第4圈開始輸出聲源區域的密度和速度，直至第8圈才停止流場計算的迭代.

采用聲學軟件Actran的直接頻域響應方法進行輔助變流器內外氣動噪聲傳播計算時，將風機旋轉交界面和輔助變流器內部流道區域分別定義為面聲源和體聲源. 為了能將流動計算所得各時間步輸出的速度和密度有效輸入到兩類聲源中，需要進行圖1所示的ICFD轉換步驟. ICFD轉換首先進行FFT變換，將速度和密度時域量轉成頻域結果，然后采用積分法插值映射到聲學網格中. 由于通常聲學網格尺寸遠小于流體網格，因而映射過程必然帶來誤差. 應該指出的是輔助變流器的聲學網格約為所對應區域流體網格的一半，映射誤差較小. 在高性能圖形工作站（128 G內存，8核CPU）上，以10 Hz為頻率間隔，完成一個工況的計算大約需要24 h.

3 數值仿真方法驗證

輔助變流器噪聲試驗在凌晨于空曠的制造車間進行，將輔助變流器吊裝在臺架上，柜體底面距離地面1.05 m，噪聲測點如圖6所示. 柜體頂部兩個進風口，正上方1 m分別布置1#和2#傳聲器；柜體四周離板中心1m 分別布置 3#、4#、5#和 6#傳聲器；柜體底部出風口正下方0.4 m和0.885 m各布置7#和8#傳聲器；柜體底部離板中心0.4 m布置9#傳聲器. 試驗過程中發現，輔助變流器處于滿載工況時，噪聲較大且呈現明顯的風機基頻噪聲.

圖6 噪聲試驗測點示意Fig.6 Measuring point location for noise test

對于旋轉機械噪聲問題，式（5）右邊第1項為Lighthill面聲源，第2項為Lighthill體聲源，Actran軟件的體聲源與面聲源設置與之對應. 分別基于面聲源、體聲源、面聲源+體聲源的設置，通過仿真計算可以得到各測點的聲壓級頻譜. 圖7為7#測點的聲壓級頻譜. 由于噪聲能量主要集中在中低頻，即290 Hz附近，超過900 Hz的聲壓級較小，因此主要分析10～900 Hz的對比結果. 從圖7可以看出，噪聲曲線最大峰值頻率為290 Hz，對應第1階葉頻；基于面聲源的曲線與基于面聲源+體聲源的曲線吻合度較高，說明單獨考慮面聲源和同時考慮面聲源與體聲源差異較小，面聲源對輔助變流器噪聲貢獻率較大，后續類似計算可只考慮面聲源，而忽略體聲源.

圖8給出7#～9#測點仿真與試驗對比曲線.從圖8（a）可以看出，距出風口0.4 m的7#測點仿真結果與試驗吻合度較高，290 Hz頻率處峰值僅相差3 dB（A）. 仿真和試驗得到的總聲壓級分別為79.8 dB（A）和 82.3 dB（A），相差 2.5 dB（A）. 由于輔助變流器噪聲主要集中在三倍頻范圍內，為便于曲線的清晰對比，故在圖8（b）和圖8（c）的對比曲線中只展示0～900 Hz頻譜曲線. 從圖8（b）可以看出，距出風口0.885 m的8#測點仿真與試驗得到的總聲壓級分別為 74.1 dB（A）和 76.8 dB（A），相差2.7 dB（A）. 從圖 8（c）可以看出，距輔助變流器底部中心點0.4 m的9#測點仿真與試驗得到的總聲壓級相差較小，但在290 Hz處有稍大差距，約為4.0 dB（A），這可能是仿真未考慮固體邊界對出風口傳播出來的噪聲吸收或耗散作用.

圖7 7# 測點聲壓級頻譜Fig.7 Sound pressure level spectrum of measurement point 7#

圖8 不同測點聲壓級頻譜仿真與試驗對比Fig.8 Comparison between numerical simulation and test for sound pressure level spectrum at different measuring points

除290 Hz頻率外，仿真與試驗的聲壓級頻譜均在70、105、250 Hz出現極大值，這可能與空腔模態有關，即發生空腔共振. 為了準確了解是否發生空腔共振，使用Actran軟件進行模態計算，得到輔助變流器流道的前20階空腔模態頻率，如表1所示. 從表1可以看出，空腔的第1階、第3階和第9階模態頻率分別為 70.14、106.44 Hz和 247.14 Hz，與 70、105 Hz和250 Hz非常接近. 可見，這些頻率出現極大值應是發生空腔共振，在后續優化中，應予以避免.

表1 前20階空腔模態頻率Tab.1 20 lowest-order mode frequencies of cavity Hz

4 噪聲超標原因分析與降噪措施

4.1 噪聲超標原因分析

通過噪聲試驗可知輔助變流器噪聲超標1.5 dB（A），不滿足主機廠提出的噪聲指標要求，為此，可以分別從聲源和聲傳播兩方面尋找原因. 圖9給出頻率為290 Hz的面聲源+體聲源仿真得到的表征聲源強度的應力張量云圖. 結合圖9（a）的整體分布結果和圖9（b）的截面分布結果可以看到，噪聲來自風機，表現為風機周期性旋轉而導致明顯的離散噪聲. 風機區域應力張量值遠大于其它區域，若風機附近隔板或壁板隔聲量偏弱，會出現噪聲直接穿透的情況. 進風口區域應力張量值較小，不是主要噪聲源.

圖9 氣動噪聲源的應力張量分布云圖Fig.9 Stress tensor distribution nephogram of aerodynamic noise source

圖10 給出頻率為290 Hz聲傳播的聲壓級分布云圖，可以看出，噪聲從風機產生后，通過流道傳播到輔助變流器進出風口. 由于輔助變流器兩個進風口有吸聲材料，內外聲壓級差距明顯，表明該吸聲材料布置和吸聲效果較好. 出風口處僅有濾網無吸聲材料，內部噪聲直接傳遞出來，出風口處聲壓級比進風口大. 由于輔助變流器柜體壁板隔聲，內部聲壓級比外部聲壓級約大35.0 dB（A）.

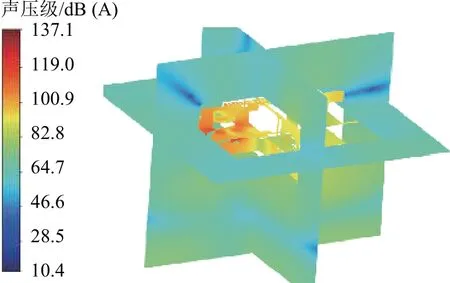
圖10 聲傳播的聲壓級分布云圖Fig.10 Sound pressure level distribution of sound propagation

通過以上分析可知，輔助變流器噪聲超標的原因之一是風機噪聲過大. 為了進一步明確風機噪聲產生機理，提取0.18 s時刻風機的漩渦分布如圖11所示. 從圖11可以看到漩渦主要在葉片前緣產生，而且前緣靠近上輪轂面漩渦分布最廣. 漩渦越過葉片前緣后逐漸開始脫離葉片表面，并慢慢向葉片壓力面擴散，擴散后大渦經過葉片出口傳遞到輔助變流器柜體出風口區域. 風機漩渦過多且強度過大是其噪聲超標的原因所在. 除風機葉片自身不合理外，還可能來自風機進口處不均勻的速度分布.

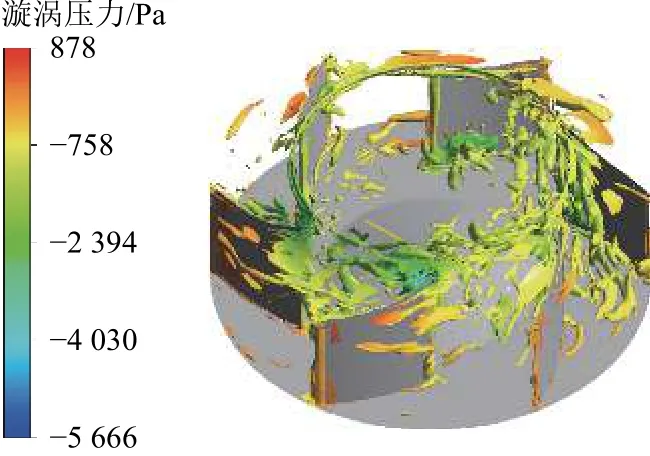
圖11 風機區域漩渦分布云圖Fig.11 Vortex distribution nephogram of fan region

4.2 降噪措施

為了改善風機進口速度不均勻，在風機進口端增加整流網. 整流網網孔為邊長5 mm的正方形，厚度為15 mm，如圖12所示. 加裝整流網并經仿真計算發現，風機流量無明顯改變，但速度不均勻度降低，風機進口速度均勻性得到改善.

圖12 方形整流網Fig.12 Square honeycomb

圖13 為有無整流網時7#測點聲壓級頻譜對比.可以看出，增加整流網后的輔助變流器氣動噪聲特性仍表現為290 Hz頻率處出現峰值，然而該頻率峰值由原來的 74.3 dB（A）降低至 72.9 dB（A），降幅為1.4 dB（A）. 另外，在原來空腔共振頻率70 Hz和250 Hz等頻率處噪聲均明顯降低. 增加整流網后，總聲壓級降低2.5 dB（A），解決了輔助變流器噪聲超標1.5 dB（A）的問題. 該措施應用在產品中進行噪聲測試，發現各測點的噪聲頻譜與仿真結果的趨勢基本一致，總聲壓級降低2.4 dB（A），降噪效果較為明顯，說明降噪方案的可行性和仿真方法的準確性. 現已將增加整流網的降噪方案成功應用到產品中.