一類發散級數階的估計

彭建華，杜 燕，范崇秀

（重慶理工大學 數學與統計學院，重慶 400054）

發散級數在數學史上具有重要地位，它與微積分的發展密不可分，被廣泛應用于數學研究以及物理等其他學科中［1-2］。發散級數在函數表示或者計算中有著重要的意義。本文利用文獻［3-5］中階的估計方法，對一類發散級數的階進行了估計。

定理1設bn ＞0，且an ＝o（bn），n→∞。則有

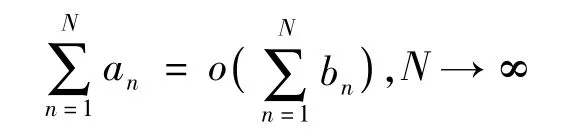
證明由假設知，對任意ε＞0，存在M＞0，當n＞M時，恒有

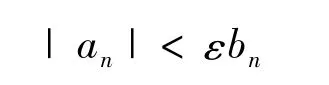
因此，對任意N＞M，有

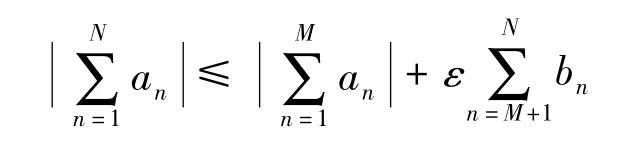
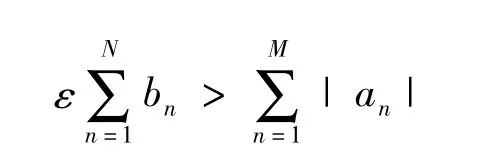
Stolz定理在數學分析中用來證明或者計算某種類型極限時是很有用的一個定理，但在文獻［6-7］等數學分析書上關于該定理的證明都非常復雜，下面利用定理1，給出一個簡單的證明方法。

例1（Stolz定理）設數列｛yn｝單調遞增，yn→∞，n→∞則

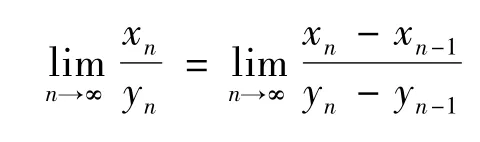
此處假定右端的極限存在。

證明設則

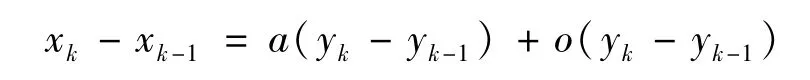
對k求和，得

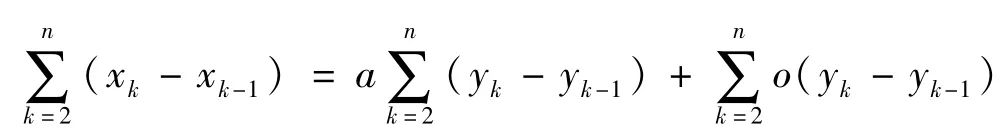
由于yn＋1＞yn，yn→∞，所以，由定理1可得

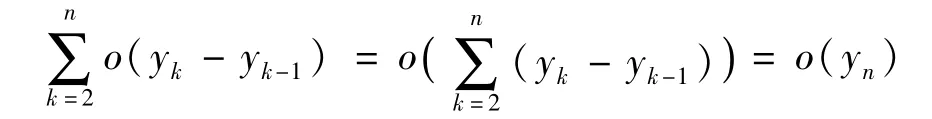
由此得到xn-x1＝a（yn-y1）＋o（yn）。將上式同除以yn，可得

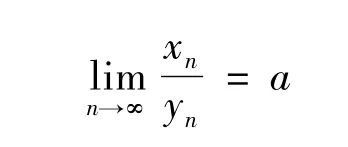
如果a＝＋∞，則可以推得數列｛xn｝單調遞增，且xn→∞，n→∞，由已證得的結論得如果a＝-∞，推導過程類似。

定理2設（bn ＞0）在區間［0，1）收斂。又1-），且an ＝o（bn）（n→∞），則 有f（x）＝o（g（x）），x→1-。

證明由假設知，對任給的ε＞0，存在N，當n＞N時，有｜an｜＜εbn，所以當0≤x＜1時，有

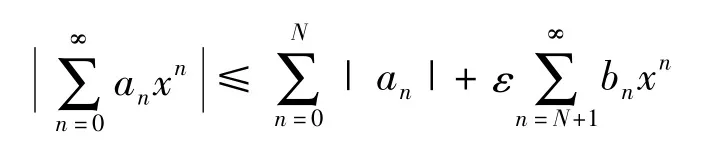
由于g（x）→∞（x→1），所以存在δ＞0，當1-δ＜x＜1時，有

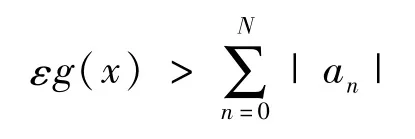
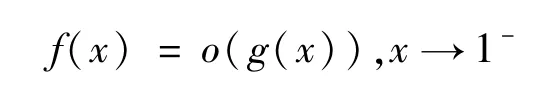
定理3設（bn ＞0）在區間［0，1）收斂。又1-），且an ～bn（n→∞），則f（x）～g（x）（x→1）。

定理4設級數f（x）和g（x）＝在區間［0，1）內收斂，令

且滿足條件

1）tn＞0；

3）sn＝o（tn），n→∞；

則有f（x）＝o（g（x）），x→1。

證明由冪級數乘法定理，得

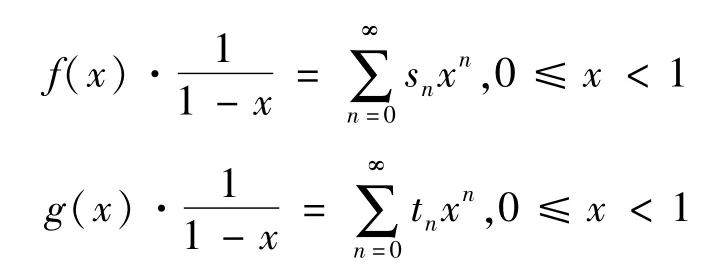
由假設條件及定理2，得

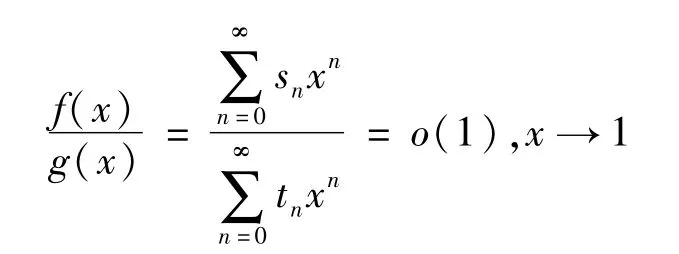
定理5若定理4中的條件（3）換成sn～tn，則有f（x）～g（x），x→1。

例2證明：

證明由于，所以

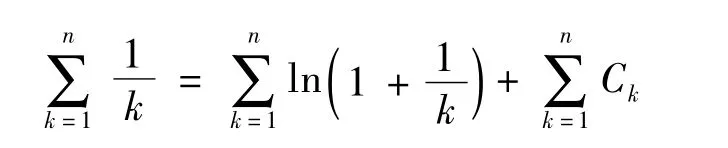
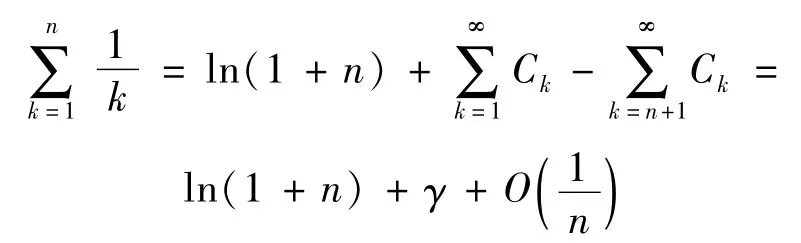
這里γ是一常數，因此證明了n→∞。

例3 設an～lnn，n→∞，則

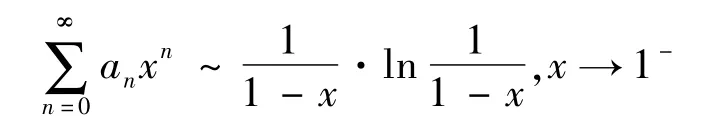
證明因為

例4 證明lnΓ（n）這里C為一常數。

證明 由于lnΓ（n）＝ln（（n-1）！）＝而

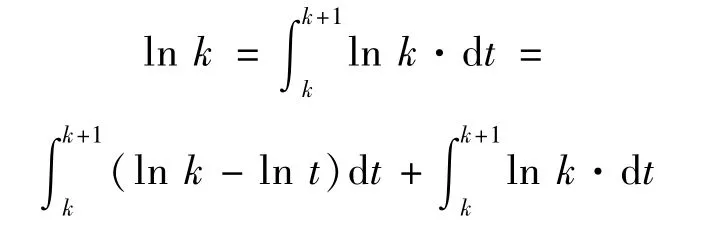
這里C為常數。