一種頻率跟蹤式磁耦合無線充電系統設計

熊 蕾，馬小三，程 祥

（安徽工業大學電氣與信息工程學院，安徽馬鞍山243000）

與傳統的充電技術相比，無線電力傳輸（Wireless Power Transfer, WPT）系統在充電領域中，因具有方便、美觀等特點，使它在電動汽車充電中有了光明的前景.本文通過分析SS型磁耦合諧振式無線電能傳輸（Magnetic Coupling Resonant Wireless Power Transfer，MCR-WPT）系統的電能傳輸理論[1-2]，推導出工作頻率特性、系統總阻抗、耦合系數以及效率之間的公式，進而引出負載及耦合系數變化會使系統產生頻率分岔的現象.并用MATLAB軟件模擬出系統的電壓增益和阻抗相位角在不同條件下隨頻率變化的曲線圖，通過分析曲線圖提出一種可使輸出電壓恒定的頻率跟蹤控制系統，并對系統的實用性[3]進行了討論.

1 電磁耦合諧振傳輸系統

MCR-WPT 系統是以法拉第電磁感應定律為基礎，在線圈的端子處加入補償電容，組成兩個LC電路，且兩個LC電路具有相同的諧振頻率.當發射端變成LC 電路諧振時，發射端回路阻抗最小，發射線圈的電流最大，那么發射線圈周圍就會有強大的電磁場.若此時接收端的LC電路頻率等于發射端，則接收端的LC 電路也發生諧振，且兩邊達到共振.由于兩個線圈產生強磁耦合諧振，使發射線圈的能量通過諧振耦合最大化地傳遞給接收線圈[4].

MCR-WPT 應用于電動汽車的整體電路結構如圖1所示.圖中Vdc是直流輸入電源；四個MOS管Q1～Q4由占空比接近但小于50%的方波信號驅動，以避免逆變器出現瞬間短路情況；C1與C2分別為初級和次級的補償電容；L1與L2為初級和次級線圈的自感；由二極管D1～D4組成的全橋整流器雖然會由于固有的壓降而降低系統效率，但其簡單、可靠和低成本性使其成為工業應用的理想選擇；C 為整流后的濾波電容，它可濾除負載RL兩端的雜波.

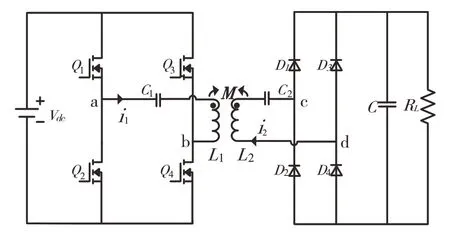
圖1 MCR-WPT系統主電路拓撲Fig.1 MCR-WPT system main circuit topology

2 電磁耦合系統補償電路的分析

由于原副邊均需要補償，故形成了4 種基本的補償技術，分別是串串型（series-series, SS）、串并型（series-parallel, SP）、并串型（parallel-series, PS）和并并型（parallel-parallel, PP）. 其中，初級采用補償電容，是為了增加發射端的線圈自感以及整個電路的電感，盡可能地讓整個系統的功率因數接近1.次級采用補償電容僅僅是為了減小接收線圈的漏感，讓其接收到最大的功率并提供給負載. 在4 種基本的補償拓撲結構中，目前使用最多的是SS 補償拓撲，其次是SP 補償拓撲. 這是因為并聯諧振補償（PS，PP）技術等效為一個電流源，而補償拓撲的輸入通常是方波電壓，若初級采用并聯諧振補償，當電壓極性改變時，初級并聯補償電容的電壓立即上升至電源電壓，造成瞬間大電流，大大縮減電容壽命[5]. 所以，SS 和SP 補償拓撲更適用于MCR-WPT 系統.圖2為4種補償拓撲的電路圖.

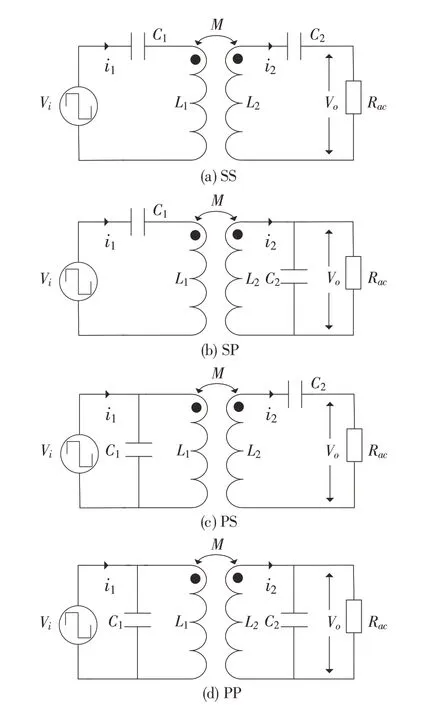
圖2 4種補償拓撲Fig.2 Four compensation topologies

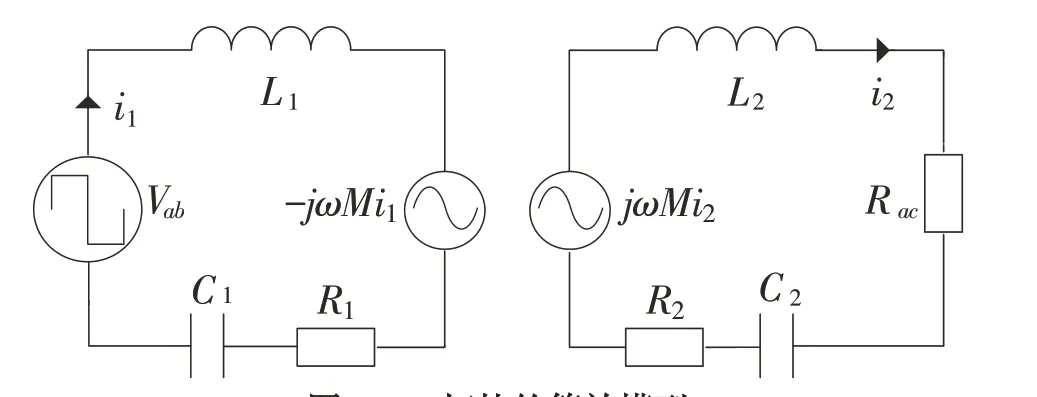
圖3 SS拓撲的等效模型Fig.3 Equivalent model of SS topology

3 SS 補償拓撲

根據上節可知，相比于PS和PP補償技術，SS和SP補償更適合MCR-WPT系統.而在SS和SP這兩種拓撲中，本文選擇的是SS 拓撲. 為了更好地理解SS拓撲結構，對圖2(a)中的SS拓撲進行了等效，等效模型如3所示.

圖3中，Vab是逆變器的輸出，它是一個方波；R1和R2分別為初級線圈和次級線圈的內阻；Rac是模擬整流器和負載電阻RL的交流等效負載電阻，其關系為[4]：

由于應用了諧波近似法，且在串聯諧振系統中，功率只在一次諧波中傳輸，因此，可以假定初級和次級的電流都為純正弦波，根據KVL定律可得：

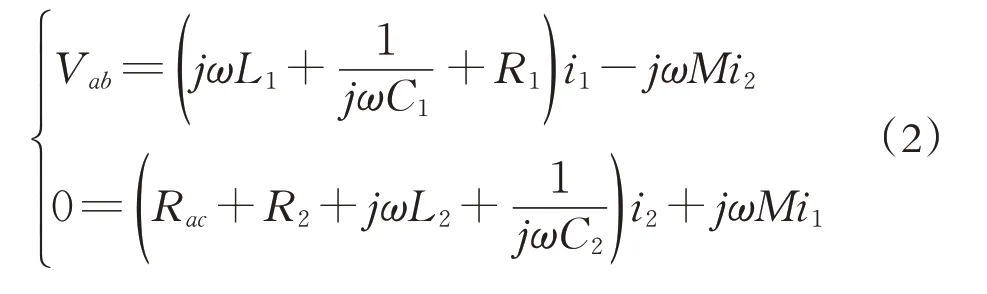
經化簡可得i1與關系i2為：

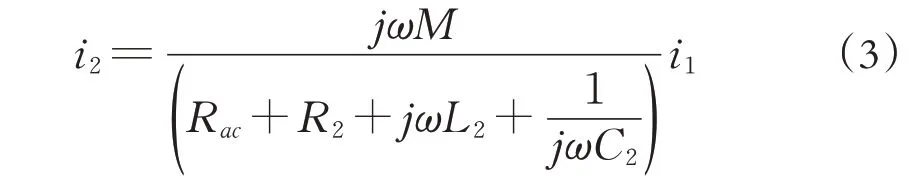
根據方程（2）、（3）可以確定全橋逆變器的總輸入阻抗ZT為:

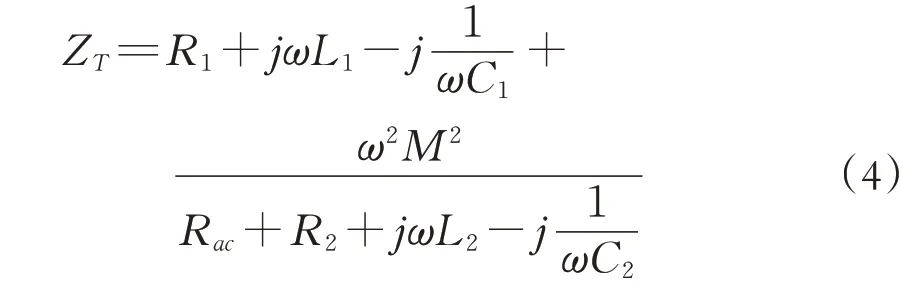
將公式（4）寫成實部和虛部的形式：

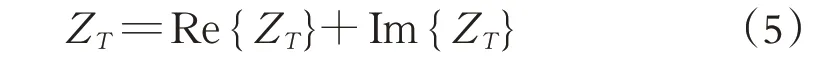
在公式（5）中，ZT可分為輸入電阻Re{ }ZT和輸入電抗Im{ }ZT，分別描述的是系統的有功功率和無功功率，它們各自的表達式為：

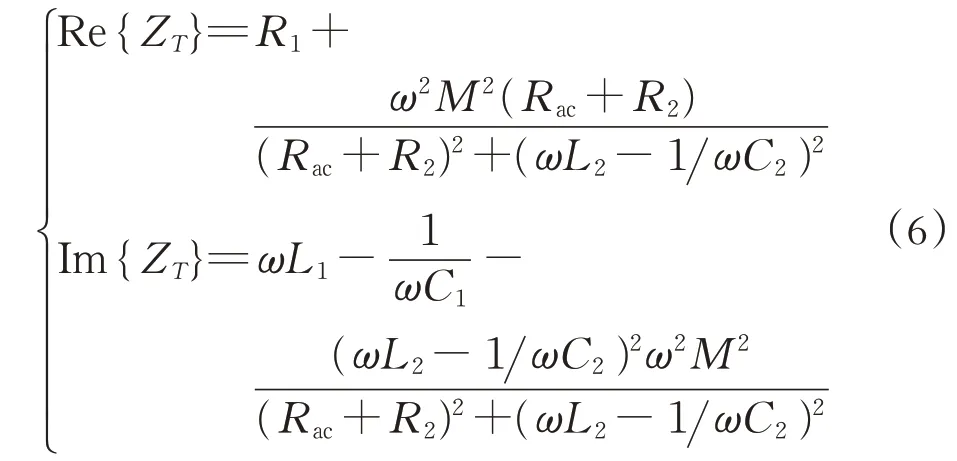
若假設V0為Rac兩端電壓，則可求得V0、Vab與i1的關系為：

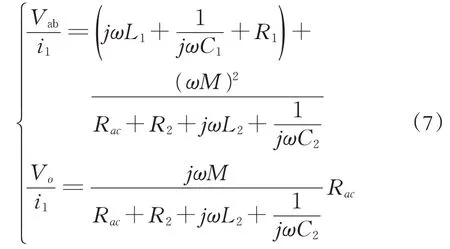
由公式（7）可解出原邊電流i1與ZT的關系為：

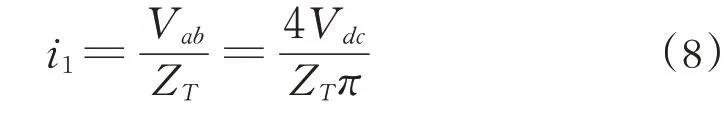
若初級電容電壓為VC1，為方便選擇電容，可根據i1求得VC1為：

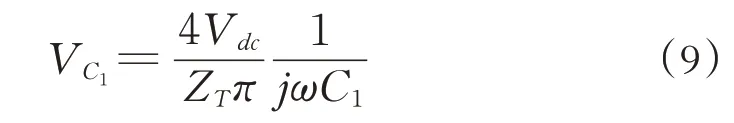
根據公式（2）、（3）、（8）可求出輸出電壓V0為：

由此推導出全橋逆變的輸入功Pin和全橋整流輸出功率Pout分別為：

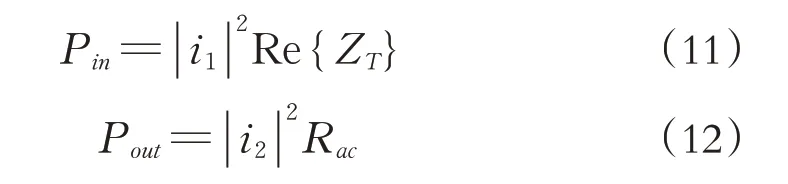
根據公式（11）和（12）得出系統效率為：

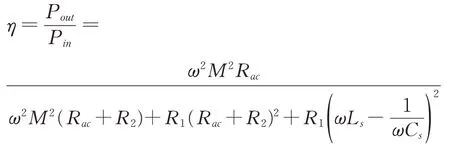
4 頻率分岔現象

MCR-WPT 系統增加兩個電容器并分別與初級和次級線圈中的電感形成了兩個諧振腔，即一個雙諧振電路. 在此雙諧振電路中，多于一個零相位角（Zero Phase Angle, ZPA）頻率是非常常見的. 這種存在不止一個ZPA 頻率的現象稱為頻率分岔[6].為了更形象的說明頻率分岔，根據公式（6）中系統總阻抗虛部的表達式，在MATLAB中作總阻抗虛部和頻率分別與互感以及負載的三維關系圖，得到圖4，其中，圖4(a)顯示了總阻抗的虛部與頻率和負載的關系，圖4(b)顯示了總阻抗的虛部與頻率和耦合系數k的關系.

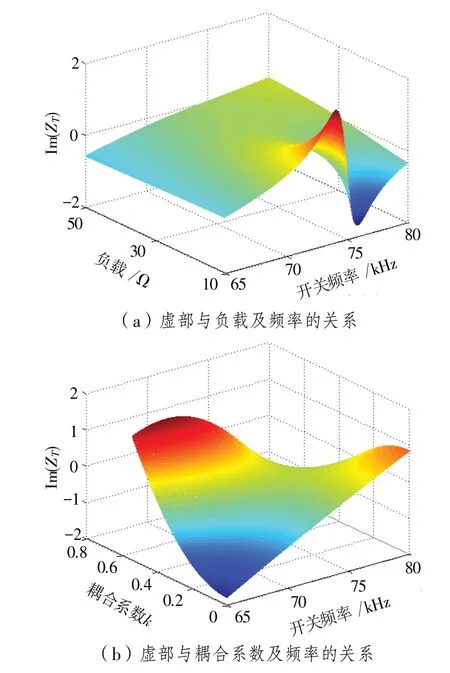
圖4 阻抗虛部與負載、耦合系數及頻率的三維關系Fig.4 The three-dimensional relationship between the imaginary part of impedance and the load,coupling coefficient and frequency

從4(a)圖中可以看出，當從初級側看次級側的負載變化時，在次級側負載很大時，系統只有一個頻率對應Im{ZT}=0，然而，隨著負載的減小，出現了一個以上的ZPA頻率.從4(b)圖中可以看出，在緊耦合條件下，系統具有一個以上的零相位角頻率. 隨著耦合系數k的減小，系統僅出現一個ZPA頻率.因此可以得出：當負載RL和耦合系數k超出一定范圍，MCR-WPT系統就會出現頻率分岔現象.

5 系統的電壓增益與阻抗相位角曲線分析

WPT系統作為一個電源系統，通常希望它能保持穩定的電壓輸出，而開環的MCR-WPT 系統穩定性能極差. 為了解決這一問題，首先根據已經推導出的公式用MATLAB 畫出的電壓增益和阻抗相位角隨頻率變化曲線圖，然后分析由耦合系數k 和負載RL變化引起電壓增益與阻抗相位角的特性變化，最后，根據分析電壓增益以及阻抗相位角的特性，提出一種通過反饋阻抗相位角的控制方式實現頻率跟蹤，以自動跟蹤不同耦合條件以及負載下的最佳頻率，并在充電過程中通過對頻率的調整，使輸出電壓一直保持恒定.

（1）負載變化時電壓增益和阻抗相位角的特性

SS 補償拓撲在負載變化的情況下，電壓增益曲線、總阻抗相位角曲線與開關頻率的關系如圖5 所示，圖中f0是諧振頻率[7]，f1與f2是電壓增益為1的頻率點，且稱這兩點為單位增益頻率點.

由圖5 可見，在諧振頻率f0時，無論負載RL如何變化，總阻抗的相位角總是零（純電阻）[8]. 系統在f0點的傳輸功率和效率雖然很高，但其電壓增益是不可控的，另外，f0點對耦合系數的變化特別敏感.與f0點相反，在f1、f2兩點無論負載如何變化，其電壓增益都是固定的，開關管也能實現ZVS. 因此，本文選擇單位增益頻率作為開關頻率，其優點是負載的變化對系統沒有影響.在電壓增益曲線中，f1、f2兩點均不受負載影響.f2點對應的所有阻抗角、相位角的曲線均在感性區，而在感性區有利于開關管實現ZVS，提高系統的效率. 經過以上的分析，MCRWPT系統的最佳頻率最終設置在f2點.

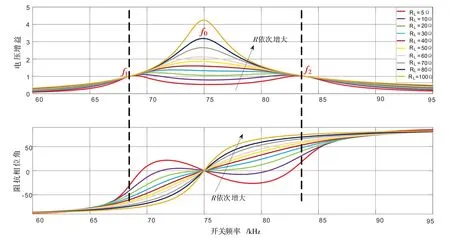
圖5 SS拓撲負載變化時電壓增益及阻抗相位角與頻率的關系Fig.5 The relationship between voltage gain and impedance phase angle and frequency when SS topological load changes

（2）耦合系數變化時電壓增益和阻抗相位角的特性

SS 補償拓撲的MCR-WPT 系統在耦合系數k變化時的電壓增益與開關頻率的關系如圖6所示.

根據上節中的分析結果，最佳開關頻率點選擇了電壓增益為1 的點，即單位增益頻率f2點，f2點的值是大于f0（75 kHz）的，對應于圖6中的右半區. 在6 圖中黑色的粗實線代表的是電壓增益為1 的所有點的集合，所以，黑色粗實線與右半區中的電壓增益曲線交點即為f2點.很明顯，當k發生變化時，f2點也在隨之變化，且k 越大f2點越遠離f0. 另外，對于k 值為0.4、0.5、0.6 對應的三條曲線，甚至出現了兩個f2點. 可見k 值越高反而不利于系統的穩定性能，k 值很高時也不利于開關管實現ZVS. 為實現輸出電壓恒定，需要對f2進行跟蹤控制[9].

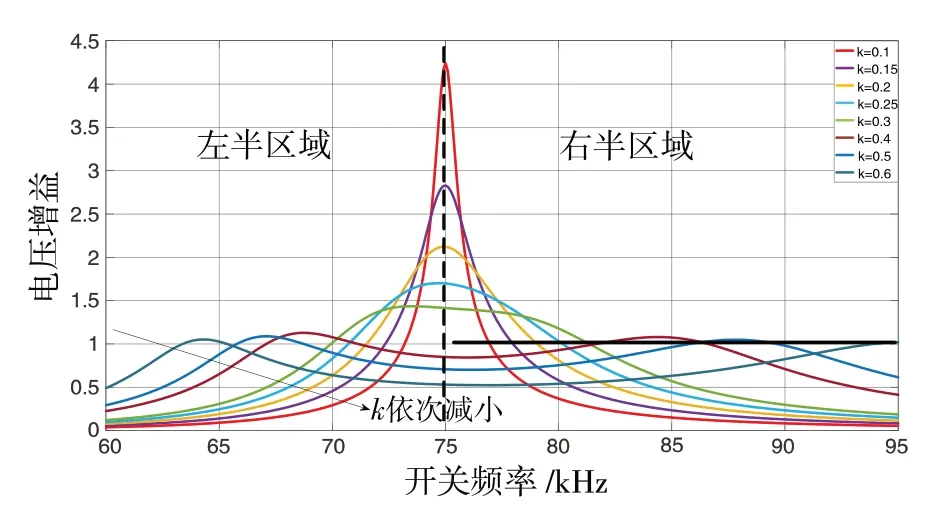
圖6 SS拓撲負載變化時阻抗相位角與頻率的關系Fig.6 Relationship between impedance phase angle and frequency when SS topological load changes

6 實驗結果

（1）軟開關波形

本文提出的頻率跟蹤控制系統，由于在每個充電周期開始時跟蹤單位增益頻率f2，且負載工作在感性區，因此，開關管可以普遍實現ZVS. 圖7 為Q1管的軟開關實驗波形圖.

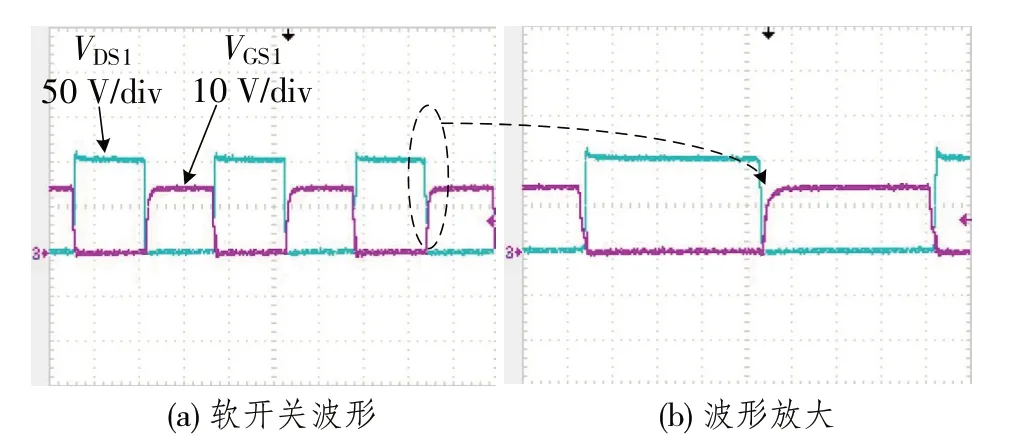
圖7 Q1管軟開關實驗波形Fig.7 Experimental waveform of Q1 tube soft switch

（2）逆變器輸出與整流輸入波形

當LC 電路發生諧振時，會濾除其它頻率的諧波，使電路擁有電流篩選的特性，所以在全橋逆變輸出方波電壓時，流過初級LC 元件上的電流為正弦波，當初級側的能量通過線圈流到次級時，由于兩邊LC電路頻率相同，次級LC上的電流也為正弦波，次級整流輸入電壓為方波，其實驗波形圖如8所示，其中圖8(a)為逆變器輸出電壓電流波形、圖8(b)為次級整流器輸入電壓電流波形.

（3）不同條件下的電壓增益及效率

當負載RL為20 Ω、50 Ω、80 Ω 時，電壓增益和系統效率隨距離變化的曲線圖如圖9 所示. 圖示僅考慮了軸向空氣間隙距離固定在6 cm時，電壓增益及效率隨線圈橫向錯位距離的變化.

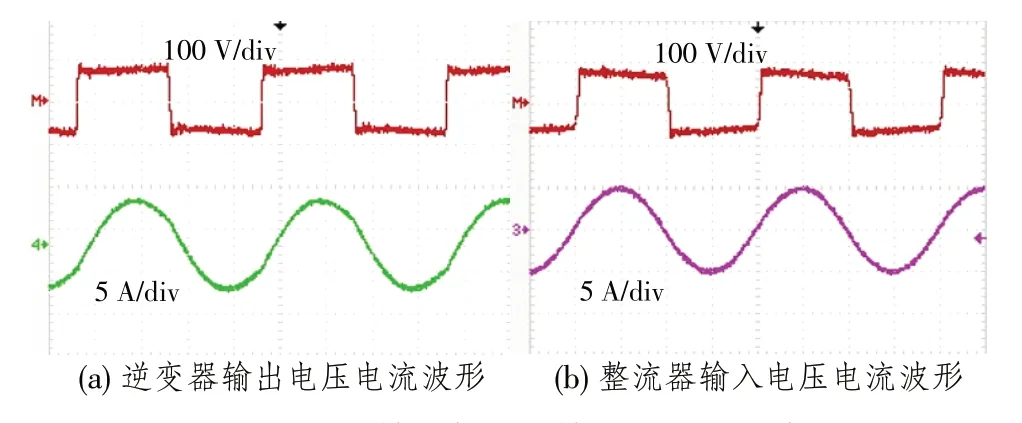
圖8 逆變器輸出與整流輸入電壓電流波形Fig.8 Inverter output and rectifier input voltage current waveform

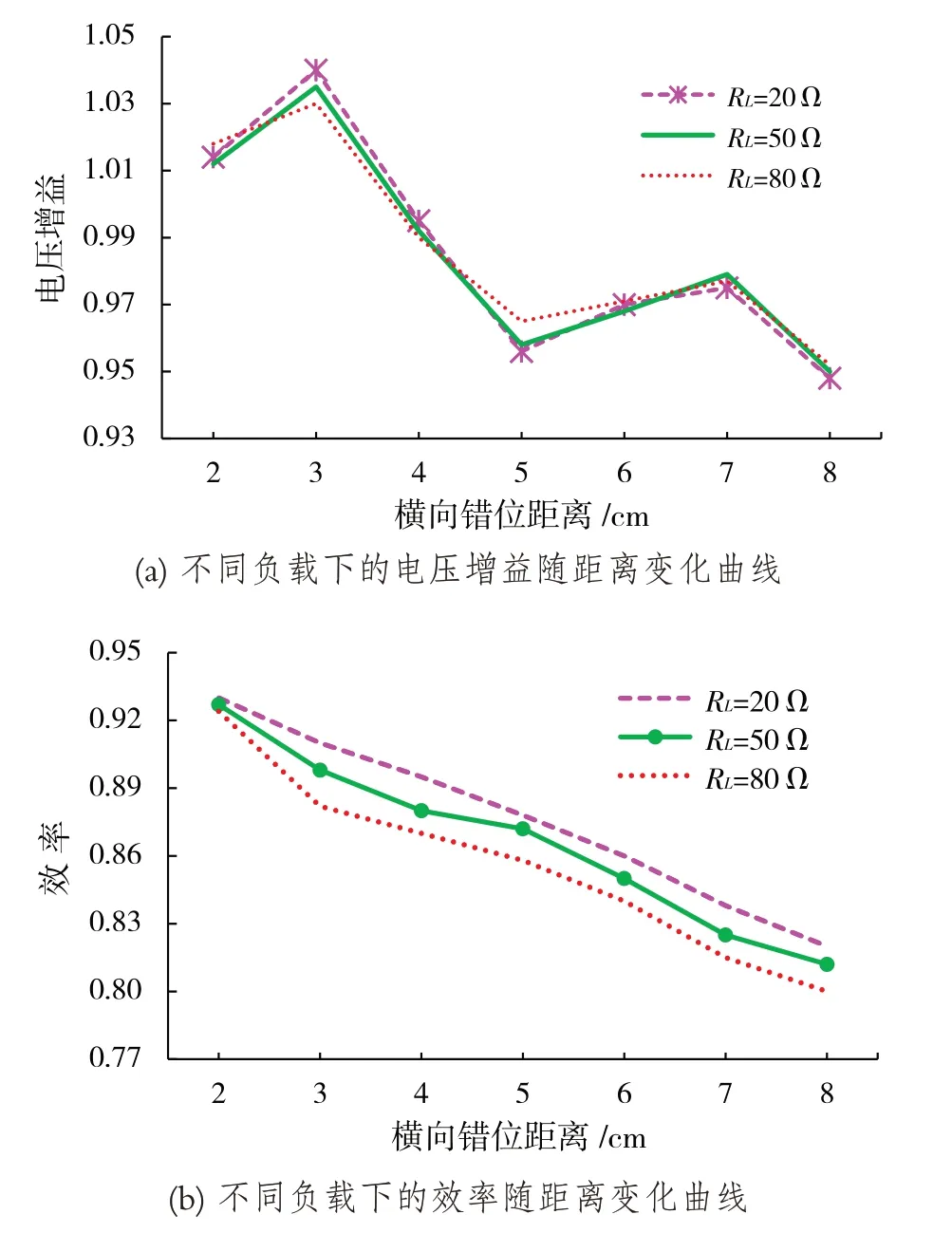
圖9 不同條件下的電壓增益及效率Fig.9 Voltage gain and efficiency under different conditions

7 結語

本文根據負載與耦合系數對MCR-WPT 系統諧振腔的影響，用MATLAB軟件模擬負載及耦合系數變化時，電壓增益與阻抗相位角隨頻率變化的關系. 在對兩種曲線特點進行詳細的分析時發現，通過對單位增益頻率點f2進行跟蹤控制，可使系統在負載與耦合系數變化的情況下實現恒壓輸出，且同時開關管可實現ZVS 控制系統簡單以及可以消除頻率分岔現象. 對幾個模塊的輸出波形進行的驗證，證明了輸出負載整體確實為感性；通過對各種實驗數據對比分析，闡明了不同負載情況下的系統輸出效率以及電壓增益隨橫向錯位距離的變化關系.