方陣及其伴隨矩陣的重要等式及應用

梁 靜，李紅菊

（安徽新華學院通識教育部，安徽合肥230088）

矩陣是線性代數的重要概念，是連接線性代數各知識點的橋梁，伴隨矩陣是矩陣運算過程中一個重要工具. 通常用伴隨矩陣求解矩陣的逆[1-2]，事實上伴隨矩陣不僅僅用于求逆，還有許多重要的關系和性質需要研究.伴隨矩陣的相關性質許多文獻都做過詳盡的闡述[3-4]，因此對伴隨矩陣的研究開始轉向矩陣與伴隨矩陣的特殊關系上[5-6]，這些關系使人們進一步認識了用伴隨矩陣解題的方法.對于正交矩陣的相關定義文獻[1][2]已經做了詳細表述，學者們也研究了正交矩陣的相關性質[7]，高小明進一步研究了擬正交矩陣的行列式，給出了相關的等價條件[8]. 本文在以上研究的基礎上，研究了矩陣與伴隨矩陣的另一個重要關系式，并由此關系等式研究了正交矩陣的相關結論，以期從另一個層面理解伴隨矩陣與矩陣的應用關系.

1 預備知識

定 義 1[1]A 是 n×n 矩 陣 ，M=是 ||A 中 第 1,2,…,r 行 和k1,k2,…,kr列交叉處的元素組成的子式，是在 ||A 中將M 所在的r行和r列全部刪去后剩下的元素按原來的順序排成的子式，稱為M 的余子式，(-1)1+2+…+r+k1+k2+…+kr與M的余子式的乘積稱為M的代數余子式.

引理1如果A是n×n矩陣(n ≥2)，那么

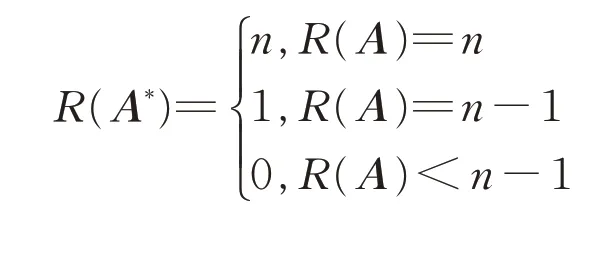
因 為AA*=det(A)I，當R(A)=n 時，有detA ≠0，則detA*≠0，即R(A*)=n. 當R(A)=n-1 時，A*中 至 少 有 一 個1 階 子 式 不 為0，則R(A*)≥1；同時有detA=0，則AA*=O，由矩陣秩的 性 質 R(A)+R(A*)≤n，有 R(A*)≤1，故R(A)=n-1 時 有R(A*)=1. 當R(A)＜n-1時，A 的所有n-1 階子式全為0，故A*為零矩陣，R(A*)=0.

引理2（Binet-Cauchy 定理）[2]設A,B 分別為n×s,s×n的矩陣，有

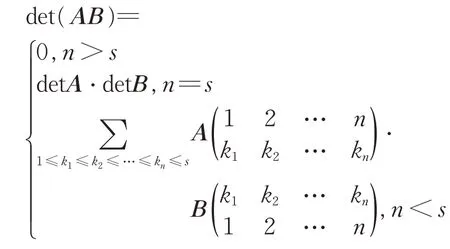
引理3（拉普拉斯展開定理） 設detA是n階行列式，任意取定r(r ＜n)個指標1 ≤i1＜i2＜…＜ir≤n，則detA 等于它的第i1,i2,…,ir行（列）元素組成的所有r階子式與它們的代數余子式的乘積和，得

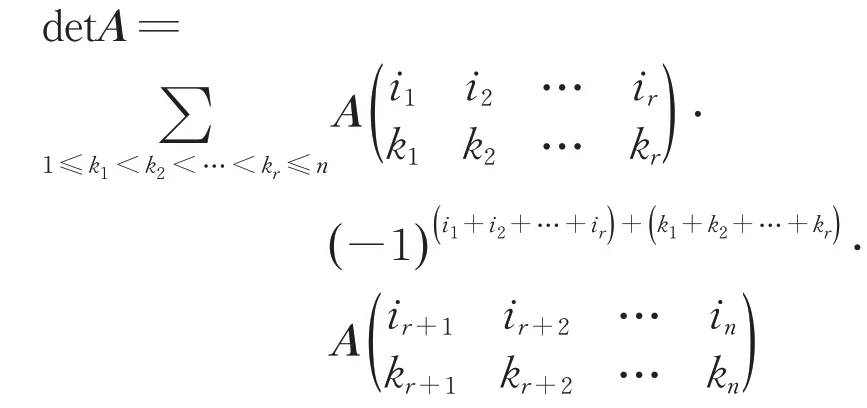
其 中 i1,i2,…,ir,ir+1,ir+2,…,in和 k1,k2,…,krkr+1,kr+2,…,kn均 是1,2,…,n 的 排 列，且ir+1≤ir+2≤…≤in，kr+1≤kr+2≤…≤kn.

2 主要結果

2.1 方陣與伴隨矩陣的等式關系

定理1若矩陣A ∈Fn×n，A 中元素aij的代數余子式為Aij，則有

其中(i1,i2,…,in),( j1,j2,…,jn)均為1,2,…,n 的排 列，且i1＜i2＜…＜ir,ir+1＜ir+2＜…＜in，j1＜j2＜…＜jr,jr+1＜jr+2＜…＜jn.

證明：（1）r=1，定理顯然成立.（2）r ≥2，有

①當det(A)=0 時，由引理1 知式（2.1）左邊為0，定理成立.

②當det(A)≠0 時，有A*A=det(A)In. 由引理2（Binet-Cauchy定理）知

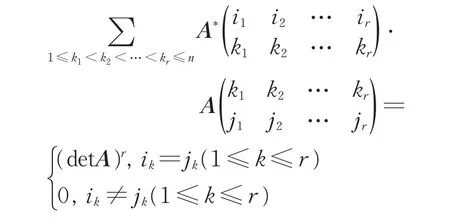
又由引理3得

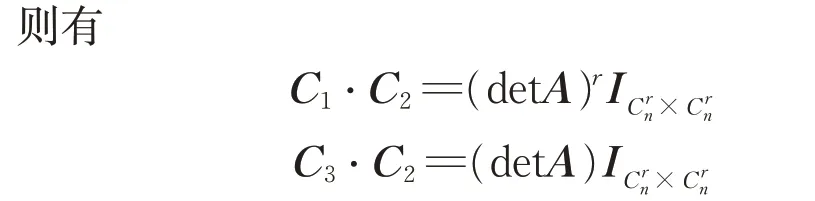
故C1?C2=(detA)r-1C3?C2.

又det(A)≠0，故 ||C3?C2≠0，有 ||C2≠0，則C2可逆. 可得C1=(detA)r-1C3，代入C1、C2并展開，由相等矩陣對應位置元素相等，因此有

推論若A為正交矩陣，則

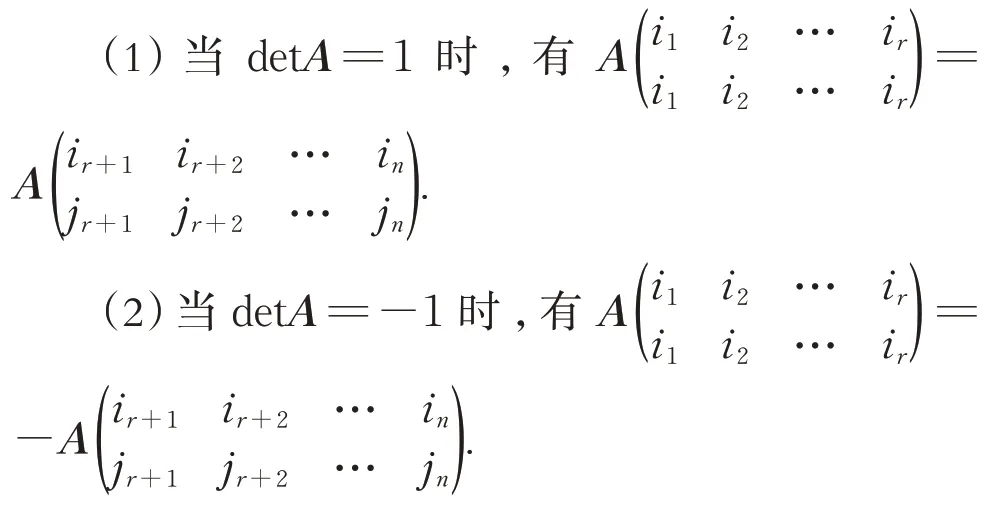
證明：（1）A 為n 階正交矩陣，則ATA=In，有

AT=A-1=A*，當detA=1時，AT=A*，即

（2）當detA=-1 時，交換A 的ik,is(1 ≤k ＜s ≤r)列得矩陣B，則detB=1，由推論（1）的結論有：

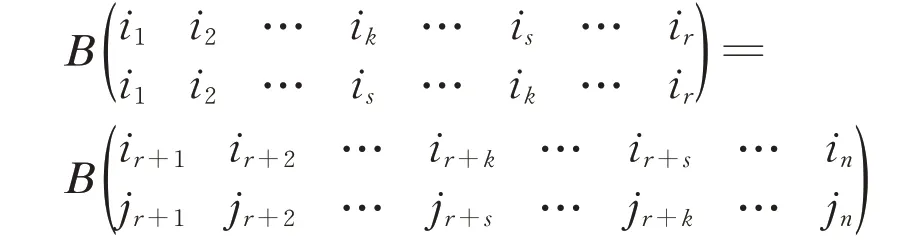
再交換B 的ik,is(1 ≤k ＜s ≤r)列得矩陣A，因此

detA=-1，detB=1，試驗證推論成立.

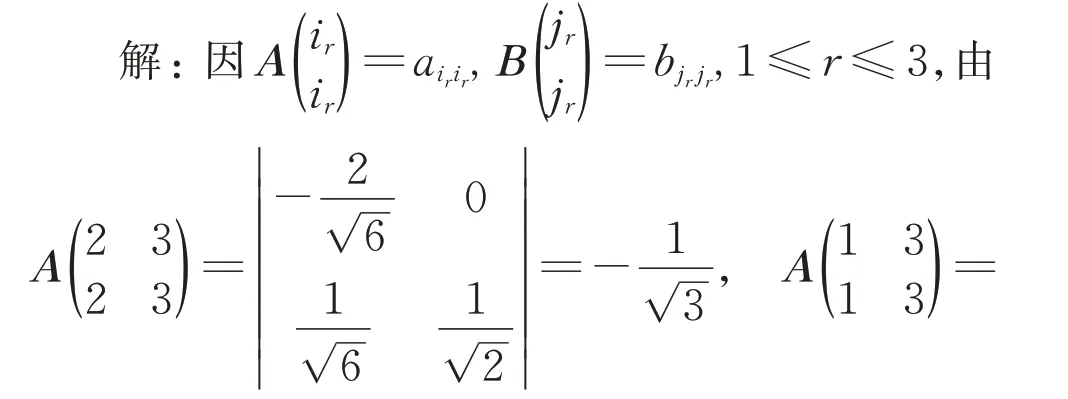
即滿足推論的結論.

2.2 等式關系的應用

例2：A 為三階正交陣，且detA=1，則(TrA-1)2+(aij-aji)2=4.

證明：

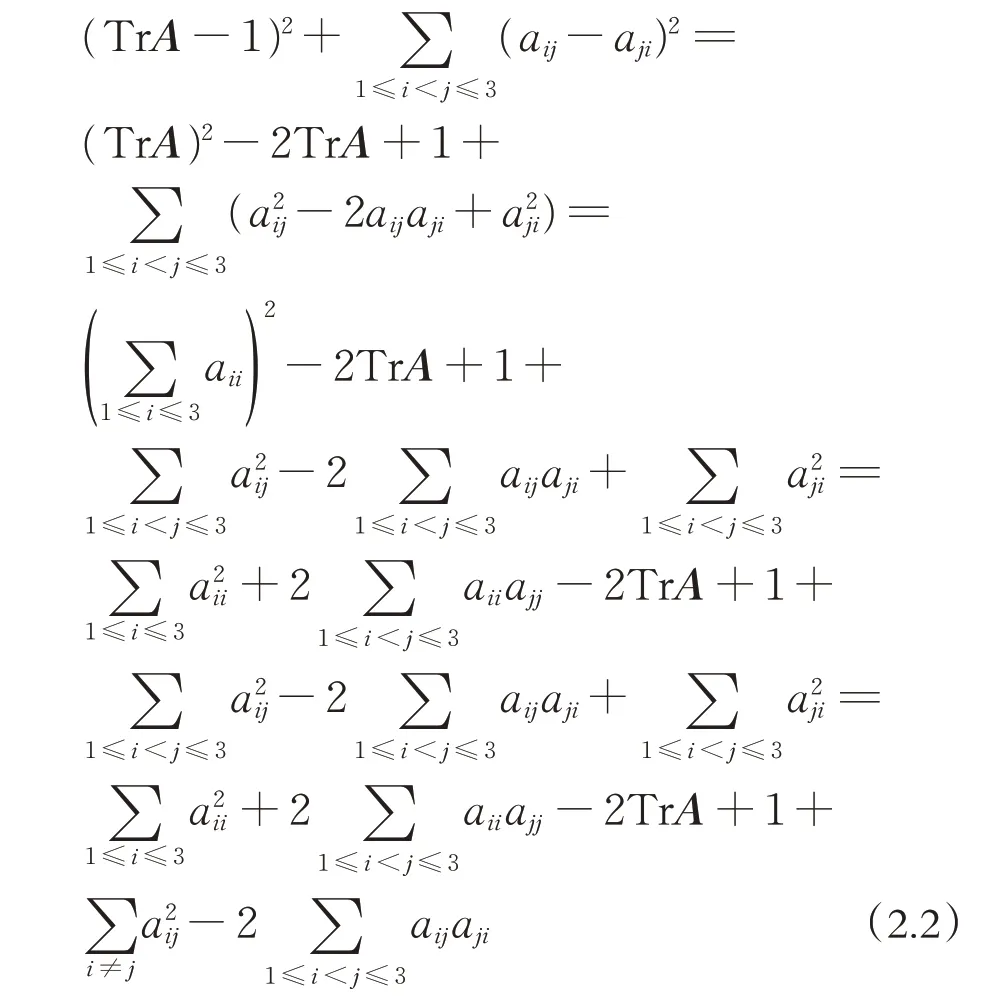
根據推論，當detA=1 時，有a11=a22a33-a23a32，a22=a11a33-a13a31，a33=a11a22-a12a21，故：

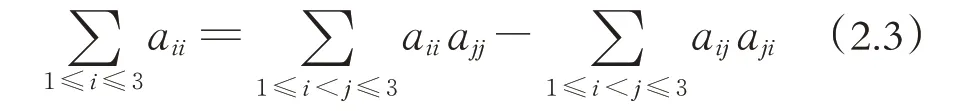
又A 為三階正交陣，則ATA=I3，則=1，1 ≤i ≤3，則有

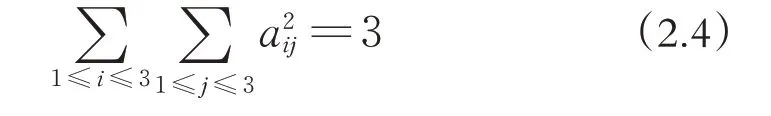
將（2.3）式、（2.4）式代入（2.2）式即證.

例3：A、B 均為正交陣，且detA+detB=0，證明det(A+B)=0.

證明：設detA=1，detB=-1，則

det(A+B)=

det(A+B)detA-1=

det[(A+B)A-1]=det(I+BA-1)

設C=BA-1，易知C也正交，且detC=-1，有

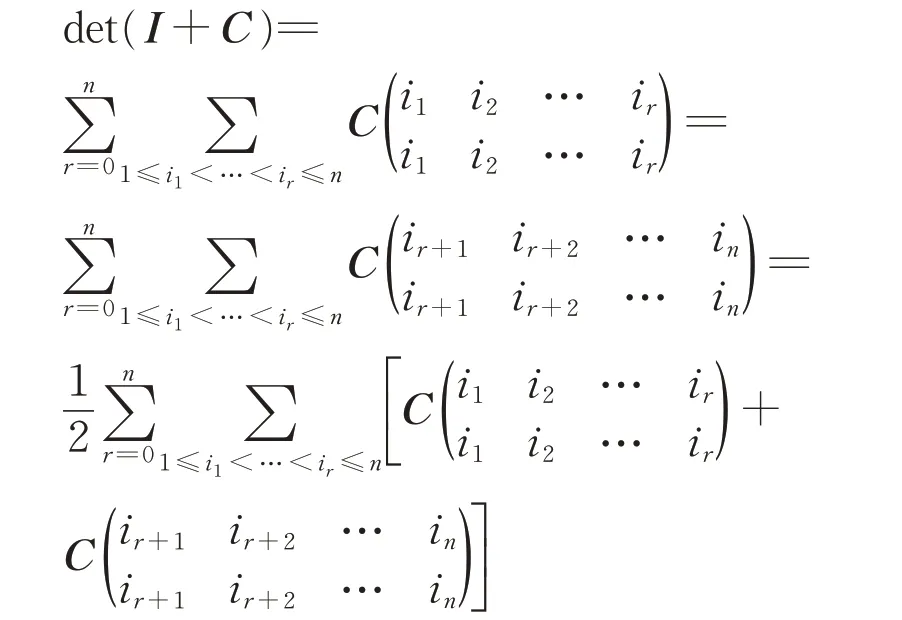
由推論知，當detC=-1時，有

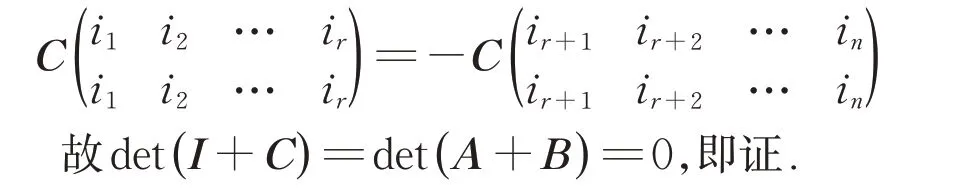
例4：①設A 為奇數階實正交方陣，且detA=1，則A 具有特征值1. ②設B 為n 階實正交方陣，且detB=-1，則B具有特征值-1.

證明：①因為A為奇數階實正交方陣，那么

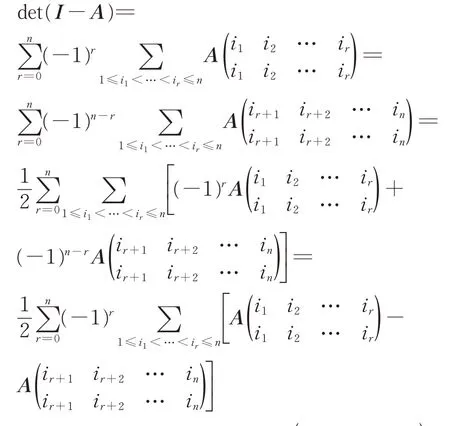
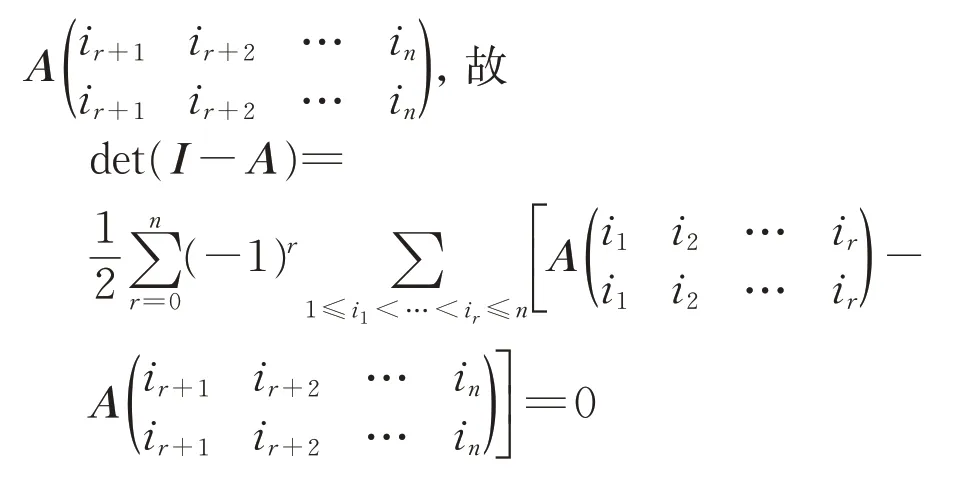
則A具有特征值1.

②由

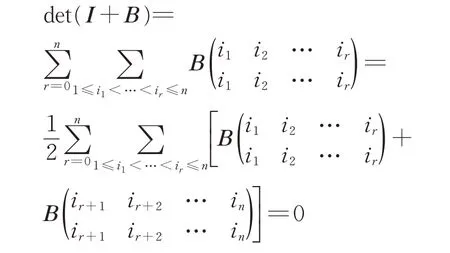
則B具有特征值-1.

另證：①設A 為2n-1 階實正交方陣，detA=1，則有

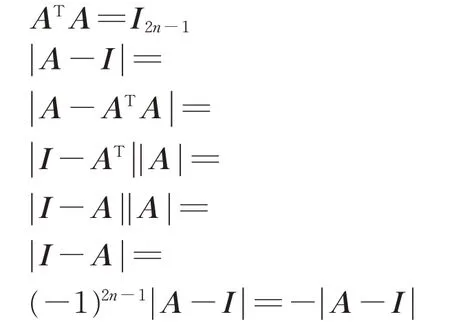
即2 ||A-I =0 ? ||A-I =0，則A 具 有 特征值1.

②因B為n階實正交方陣，detB=-1，則有

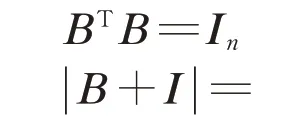
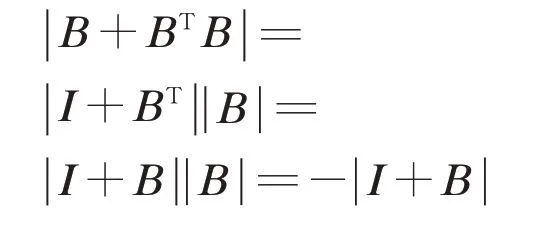
有2 ||B+I =0 ? ||B+I =0，則B 具 有 特征值-1.

3 小結

本文利用Binet-Cauchy 定理及拉普拉斯展開定理研究了伴隨矩陣A*與n 階方陣A 之間的關系，給出了具體的關系等式. 由此等式研究了n 階正交矩陣A 的r 階子式與其余子式的關系，進一步研究了正交矩陣的相關應用.這些研究更加明晰了正交矩陣余子式的相關關系，可為以后研究正交矩陣的其他應用奠定基礎.