局部差分隱私約束的鏈接攻擊保護*

楊高明，方賢進，肖亞飛

安徽理工大學 計算機科學與工程學院，安徽 淮南 232001

1 引言

研究機構和互聯網公司正在以各種方法收集個人數據，這些數據不可避免地包含個人隱私信息，如果直接發布這些數據將會導致用戶隱私信息的泄露[1-2]。如AOL（American Online）曾經發布數據用于競賽，結果導致一位老年婦人個人隱私泄露[3]。因此，必須在發布之前進行數據凈化處理，以保護個人隱私信息。隱私保護的數據發布主要關注數據的微觀方面，這種方法把記錄的屬性分為三類：（1）身份屬性（如姓名、身份證號碼、微信賬號等），其相當于數據庫的主鍵（key），可以唯一地標識個體；（2）準標識符（quasi-identifier，QI）屬性（如郵政編碼、年齡和性別等），其值的組合可以潛在地標識個體；（3）敏感屬性（如所患疾病和收入等），表明個人不想對外泄露的敏感信息。許多研究者已經發現，在發布數據之前僅僅刪除用戶的身份屬性，并不能保護發布數據表中的個人隱私信息[4-5]。QI屬性可能被攻擊者與其他公共數據集聯系起來，獲得個人的隱私信息，這被稱作數據發布中的鏈接攻擊（link attack），這種攻擊主要導致用戶身份泄露和屬性泄露。如果攻擊者可以從發布的數據中識別個人，則會發生身份泄露；而攻擊者通過屬性鏈接揭示個人的敏感屬性則會發生屬性泄露。

為應對鏈接攻擊導致的用戶身份泄露和敏感屬性泄露，學者們提出了許多隱私保護數據發布模型并試圖建立一種通用的隱私保護模型。k-匿名[3]是關系數據庫文獻中提出的第一個有影響力的模型，它使用泛化（generalization）概念來提供隱私保護，該方法將屬性的細粒度值泛化為不特定的粗粒度屬性值，以阻止攻擊者根據準標識符屬性值把具體的個人與其他k-1個體區分開來，其核心思想是確保至少k條準標識符屬性值相同的記錄在同一個組內。后來，學者引入l-多樣性[6]來解決k-匿名存在的限制，以抵御身份泄露和屬性泄露，使攻擊者無法實現同質攻擊或背景知識攻擊。t-closeness[7]進一步優化了多樣性的概念，并要求每個等價類的敏感值的分布與數據集的整體分布密切相關，在任何等價類中的敏感屬性的分布接近整個表中屬性的分布。以上基于泛化思想提出的隱私保護數據發布匿名化模型并不能完全阻止用戶的隱私泄露，后來Dwork[8]提出了差分隱私的概念，確保添加或刪除單個記錄不會顯著影響任何分析結果的輸出。差分隱私在交互式的基礎上實現隱私保護，其實現機制是添加拉普拉斯噪音或者指數噪音，目前很多研究者在差分隱私方面做了大量工作，取得了豐富的研究成果[9]。

除了以概化為基礎的匿名化和以添加隨機噪音為基礎的差分隱私之外，隨機響應方法也被用于發布數據[10-11]。該方法不像匿名化一樣將QI屬性值泛化為粗粒度值，而是根據一定的概率將原始值擾動為其他值，他們專注于評估將目標個體成功鏈接到其他記錄的風險。如Shen等人[12]假設數據擾動在客戶端進行，用戶不知道其他用戶的信息。他們的工作集中在購物籃數據或一般分類數據的隨機化，而不是在鏈接攻擊下研究隨機化的隱私泄露。Cormode等人[13]是通過引入經驗隱私和數據效用的概念來解決這些挑戰，并通過改變每個模型的相應參數來比較傳統隱私模型與差分隱私。再者，已有的基于隨機調查數據的方法并不能直接用于中心數據的發布，因為隨機調查方法的擾動矩陣P由調查者決定，與用戶數據無關，而中心數據的方法，其擾動矩陣除了受數據發布者決定之外，還受到數據分布的影響。在前人已有的基礎上，Wang等人[14]在理論上證明了隨機響應方法實現差分隱私的可行性。

以上采用隨機化實現隱私保護主要使用均勻擾動方法，沒有考慮數據的分布情況，導致數據的效用和隱私保護之間沒有得到很好的平衡[15]，本文結合數據分布的情況對數據進行擾動，即考慮擾動準標識符屬性又考慮擾動敏感屬性，其應用場景主要包括：政府部門或者企事業單位外包數據進行數據分析或者數據挖掘。具體貢獻如下：研究了鏈接攻擊下的身份披露和屬性披露問題，重點關注攻擊者得到用戶的準標識符屬性以后，成功預測目標個體敏感屬性值的風險；提出了一個隨機化技術實現局部差分隱私的框架，系統地研究了隨機化方法防止鏈接攻擊的策略，有效解決了隨機化方法實現局部差分隱私參數P選擇問題，在數據集滿足隱私保護要求的同時，最大化數據效用。最后，使用UCI機器學習庫的Adult數據集進行了廣泛的實驗，利用數據分布(KL-散度、卡方距離)有效驗證了數據的分布變化情況。

2 基本概念

設數據庫DB具有N條記錄，每個記錄具有m+1個屬性，其中A1，A2，…，Am是m個準標識符屬性，S是敏感屬性。屬性Ai(S)具有di(ds)個不同的值，用0，1，…，di-1(ds-1)表示，并使用Ωi(Ωs)表示Ai(S)的域，Ωi={0，1，…，di-1}，ΩQI=Ω1×Ω2×…×Ωm是準識別符的域，Ωs敏感屬性的域。對于給定的個體，準標識符屬性值對攻擊者是透明的，其中S表示敏感屬性，其值不應與攻擊者需要識別的個人相關聯。一般而言，數據庫DB也可能包含其他屬性，這些屬性既不是敏感屬性也不是準標識符屬性，它們通常在發布的數據中保持不變。由于這些屬性不會導致隱私泄露風險或數據效用損失，此處將不討論它們。另外，本文主要討論單敏感屬性，而多敏感屬性可以在現有討論的基礎上推廣。

隨機響應實現局部差分隱私的基本思想主要是：（1）對每一個準標識符屬性Ak，選擇屬性轉換矩陣（2）使用概率2，…，dk)隨機改變原始屬性值為擾動屬性值，使之滿足局部差分隱私要求，此處表示第k個屬性的第i個取值與之類似。隨機化過程根據每個記錄的屬性獨立執行，即執行隨機化過程不考慮記錄之間的關系，與樸素貝葉斯網絡類似，假設各個屬性之間的關系獨立，而記錄的屬性之間的關系若不獨立則需要另行考慮。確定隨機化矩陣以后就可以生成擾動數據，數據接收者根據擾動數據和擾動矩陣可以取得數據的統計特征，以及進行數據分析或者挖掘工作。

2.1 失真矩陣選擇

使用隨機化方法對數據進行隱私保護主要是尋找失真矩陣，它確定隨機數據的隱私和效用，如何找到具有隱私或效用約束的最優失真矩陣是一個具有挑戰性的問題。Huang和Du[16]應用一種進化多目標優化方法，從單個屬性的整個搜索空間中搜索最優失真矩陣。然而，由于其高度的復雜性，該方法難以處理多個屬性。目前的隨機化矩陣主要是均勻隨機化及其變種。它們將每個QI屬性Ai（或敏感屬性S）的隨機化參數限制為：

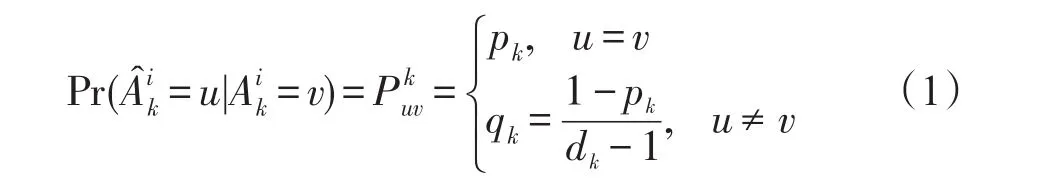
換句話說，對于每個屬性Ak的所有值，其以相同的概率pk保持不變，以概率qk被擾動到其他值。這種擾動方法主要缺點是不能反映數據的分布情況，導致數據效用下降。為解決這個問題，提出考慮原始數據分布的解決方案。

前面已經介紹了隨機響應的基本思想，下面介紹隨機響應的基本過程。對于每個記錄Ri，i=1，2，…，N，數據所有者使用失真矩陣Pk獨立地隨機化屬性Ak，k=1，2，…，m。具體來說，對于具有dk個值的屬性Ak，隨機化過程將屬性值以一定的概率替換為為方便起見用表示第k個屬性值為v轉換為值u的概率，即有：

式中，i，j=1，2，…，dk。令，則Pk稱為Ak的失真矩陣，Pk的列總和等于1。對于敏感屬性，其處理方式與準標識符屬性一樣。運用失真矩陣，可以把原始數據庫DB擾動為，然后發布隨機數據集和失真矩陣P。數據發布者發布失真矩陣，是為了讓數據分析人員了解原始數據的隨機化大小，幫助數據分析人員估計原始數據分布。

2.2 局部差分隱私

數據的隱私需求有兩種不同的上下文環境：局部隱私場景，如個人在社交網站主動披露個人信息；全局隱私場景，如機構發布包含個人信息數據庫或基于這些數據庫回答某些問題（例如，美國政府發布人口普查數據，Netflix公司等發布專有數據供他人數據分析）。對于這兩種情況都可以通過在發布數據之前將數據隨機化來實現差分隱私。本文主要研究局部隱私情況，該模式的數據提供者不信任數據收集者或者數據分析師。

隱私保護的主要目的是使攻擊者在凈化數據上推理得到與原始數據幾乎相同的結果，同時使用戶的隱私信息得以隱藏，差分隱私就是在這個概念的基礎上產生的。在差分隱私模式下，即使攻擊者具有無限的計算能力并且可以訪問數據庫中除查詢數據之外的每個記錄，也不能確定某個特定用戶是否在數據庫中。由于差分隱私具有理論基礎的支持，得到了廣泛研究和應用，最近，差分隱私的概念已經擴展到局部隱私環境[17]。實際上局部差分隱私可以看作全局差分隱私的特例，即敏感度為1的情況。

定義1（局部差分隱私）設有n個數據記錄，Ak是數據集DB的第k個屬性，其轉換矩陣為Pk，k∈{0，1，…，m}。機制 M 是將 Ak∈ΩAk隨機映射到ΩAk閾值內的任何一個值，且ΩAk內每一個閾值獨立同分布。對于非負數值ε，如果機制M是ε-局部差分隱私的，則有：

ε越小隱私保護效果越好，然而當多次查詢，耗盡ε則會導致隱私泄露，故ε的選擇也需要根據實際情況確定。

2.3 數據效用及度量標準

隱私保護的數據發布除了滿足不泄露用戶隱私信息之外，還要滿足數據分析者對數據效用的要求。發布數據的最終目標是最大限度地保留數據效用，同時降低屬性披露的風險，任何數據集的效用，無論是否隨機化，都會依賴于可能執行的任務。有許多數據效用的度量標準，匿名化使用的效用度量標準之一是數據泛化高度，它是指數據泛化步驟的總數。然而，在隱私保護的數據發布領域這種方法存在的問題是：對泛化高度相等的兩個匿名化組，其數據效用差距巨大。鑒于目前許多數據挖掘應用與數據的概率分布有關，在評估數據庫的效用時，本文采用KL-散度、卡方度量數據的效用。

KL-散度(Kullback-Leibler divergence)是離散概率分布P和Q之間的對數差，用于找到兩個頻率分布之間距離的度量，此處用于查找原始數據的分布與隨機化后的數據相同屬性分布之間的距離，即它表示當原始數據集變換為擾動數據集之后其分布信息的丟失量，其計算公式如下：

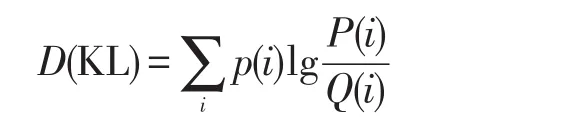
除了采用KL-散度量化數據效用，文中還采用卡方距離比較原始數據和重建數據之間的分布差異，即統計樣本的實際觀測值與理論推斷值之間的偏離程度，其決定卡方值的大小。卡方值越大，原始分布與擾動分布的差異越大；卡方值越小，原始分布與擾動分布的差異越小，若兩個值完全相等時，卡方值就為0，表明理論值完全符合。給定兩個分布P=(p1，p2，…，pm)，Q=(q1，q2，…，qm)，其卡方距離如下：

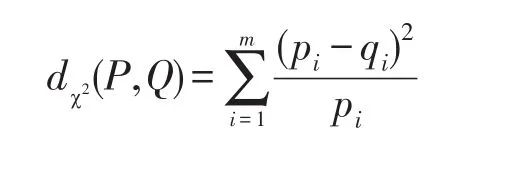
3 屬性披露和鏈接攻擊

確定隨機化概率轉換矩陣Pk以后，攻擊者將觀測值視為Ak的真實值是不合理的。相反，攻擊者可以根據觀察到的數據和發布的隨機參數來嘗試估計原始值。假設攻擊者能夠得到擾動數據集及后驗概率，并采用以下概率擾動策略：對于任何u，v∈ΩAk，在概率情況下計算其中表示當攻擊者觀察時，而實際原始值Ak=u的后驗概率。由貝葉斯定理可以得到以下計算公式：

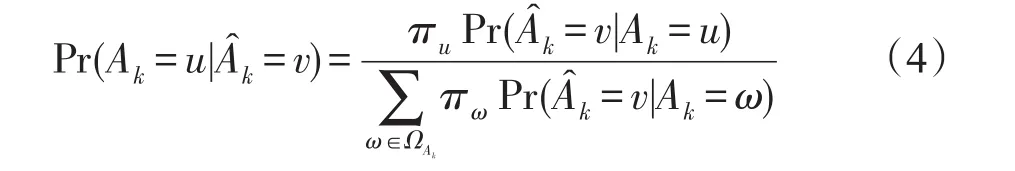
式中，πw表示Ak=ω時的概率分布。下面，分別對二值屬性和多值屬性進行討論，并進一步討論其組合。

3.1 二值屬性隨機化矩陣的構造

這種擾動方式要求每列的概率和為1，在隨機響應相關文獻中，一般設pu=pv。為有效地增加數據的隨機性和提高數據的效用，此處采用雙重擾動的方式。首先，計算二進制屬性的每一個屬性的值在數據集中所占的比例，分別為pu、pv，并根據給定的隱私保護參數ε計算出pu、pv與ε的關系。第一次擾動根據原始取值進行擾動，比如要擾動的數據值為u，則生成隨機函數，并把隨機函數以pu為界分為兩部分，若隨機值位于[1，pu]，則擾動值保持不變；若隨機值位于(pu，1]，則需要第二次擾動。每一步擾動都要根據它們在數據分布中的占比，并考慮隱私保護參數ε，具體過程見算法1。二值屬性得到的擾動矩陣PBB為：

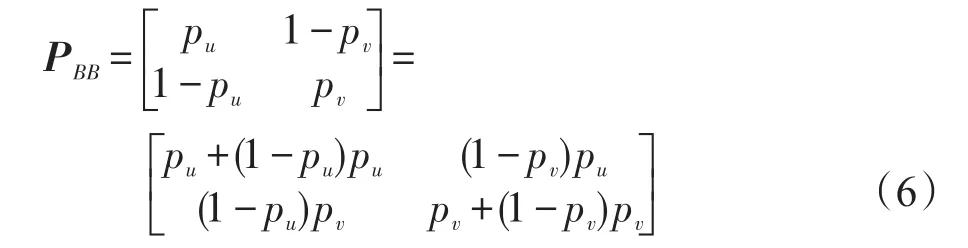
對于二進制屬性，一般采用均勻擾動，這種擾動方法把對角線元素設為p，0.5＜p≤1，該方法的優點是可以排除離群點對數據的干擾，缺點是所有數據均勻出現，違反了數據的自然規律，鑒于此，本文提出使用數據的原始分布作為隨機擾動基礎，并在隨后的實驗中分析該方法對離群點影響。下面給出二值擾動的基本方法。由于二值屬性僅僅有兩個值，可以分別用u和v表示。若u在原數據集中所占的比例為pu，則v所占的比例為1-pu。即采用的擾動矩陣PB為：

式中，puv=P(u|v)，表示原始值為v擾動為u的概率。Geng等人[18]已經理論證明了局部差分隱私的最優形式是采用樓梯機制（staircase mechanism），因此，此處令屬性值保持不變的概率為puu=pvv=eε(1+eε)，則pv=1-pu=1(1+eε)，帶入式（6），可得：

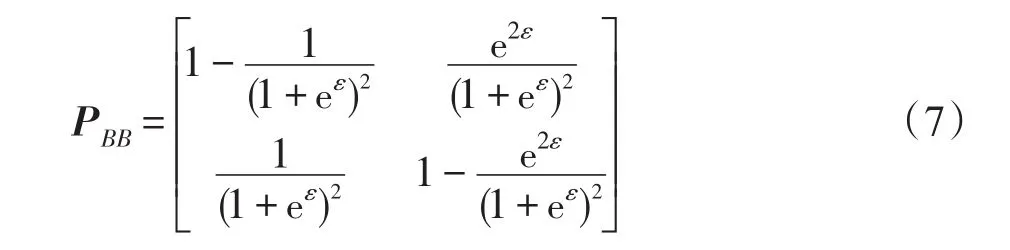
算法1二值屬性擾動算法

算法1的行1主要對數據集進行統計工作，用于計算隨機擾動方法是否滿足局部差分隱私，行3是為了確保數據分布傾斜情況下滿足差分隱私要求，行4～8用于處理屬性Ak=u的情況，行9～11用于處理Ak=v的情況。對于這兩種情況，都需要根據數據的原始分布狀態進行二次擾動。

下面討論采用PBB擾動矩陣的數據集，是否滿足局部差分隱私的要求。根據局部差分隱私的定義，此處僅僅討論給定ε的值大于或等于0的情況。另外若由pu計算得到的ε′＞0.5ε，則令ε′=0.5ε，因此僅需討論ε取最大值的情況。

（1）屬性值u擾動為u的概率為puu，擾動為v的概率為pvu，由pu計算出ε′滿足：

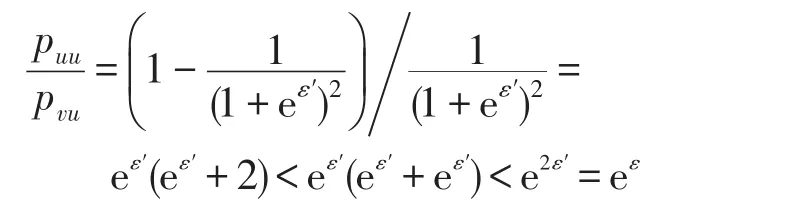
由算法1行3知，ε′≤ 0.5ε，故puu/pvu≤ eε滿足局部差分隱私。

（2）屬性值v擾動為v的概率為pvv，v擾動為u的概率為puv，則有：

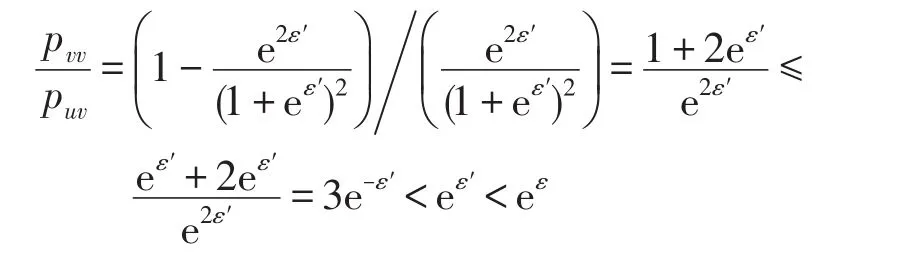
故pvv/puv滿足局部差分隱私。

3.2 多值屬性隨機化矩陣的構造

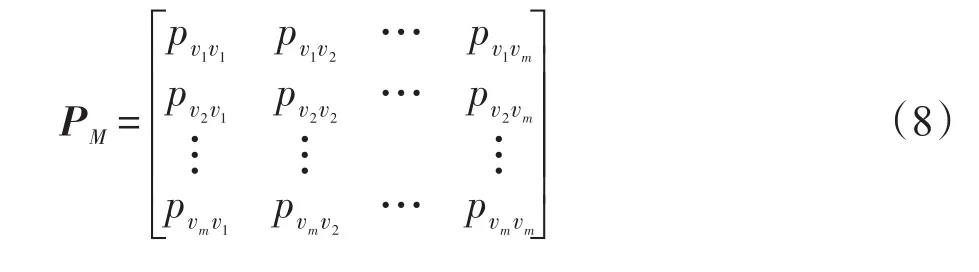
設屬性Ak具有m個屬性值，分別用v1，v2，…，vm表示。若Ak=vi(i=1，2，…，m)在原數據集中所占的比例為pvi，則采用均勻擾動有A?k=vj(j=1，2，…，m)，由此得擾動矩陣PM為：的比率pvi，把隨機函數以pvi為界分為兩部分，若隨機值位于[0，pvi]，則擾動值保持不變；若隨機值位于(pvi，1]，則需要第二次擾動，這時仍根據它們在函數中的占比進行擾動，即擾動時考慮它們在原始數據集的分布情況，具體過程見算法2。此時得到的擾動矩陣PMB為式（9）所示：

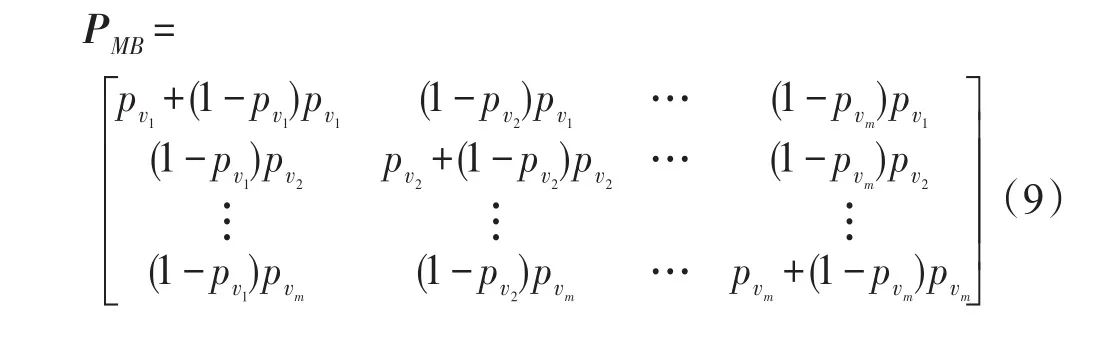
與二進制屬性的處理方式一樣，多值屬性也采用兩次擾動的方式。首先，計算多值屬性的每一個值在數據集中所占的比例，設為pvi，i=1，2，…，m，并根據差分隱私參數ε計算它們之間的關系。第一次擾動根據原始取值進行擾動，需要擾動的數據值vi所占

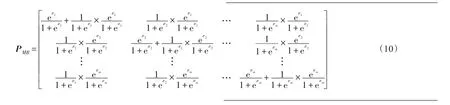
式中，pvivj=P(vi|vj)，i，j=1，2，…，m，表示原始值為vj擾動為vi的概率，與二值屬性相似，此處令pvi=eεi/(1+eεi)，i=1，2，…，m，帶入式（9）可得：

算法2多值屬性擾動算法

算法2的行1用于統計屬性Ak的每一個值所占的比例，行2、3用于設置滿足局部差分隱私的隨機擾動概率，行4～10用于處理屬性每個值的擾動。

下面討論采用PMB擾動矩陣的數據集，是否滿足局部差分隱私的要求。

（1）屬性值vi擾動為vi的概率為pvivi，擾動為vj的概率為pvivj，i，j=1，2，…，m，設由pvivj計算得到的差分隱私參數為ε′，則有：

式中，取ε=2 ln 4隨機擾動即可滿足局部差分隱私。

（2）屬性值vi擾動為vj的概率pvjvi，擾動概率為pvkvi，i，j，k=1，2，…，m，則有：

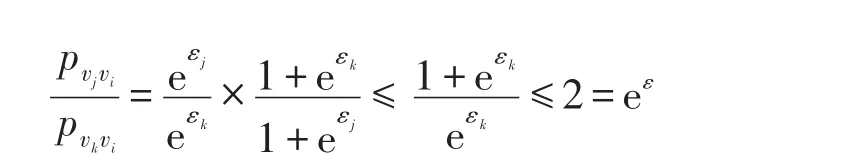
式中，ε大于等于1即可滿足局部差分隱私。

3.3 多值屬性的保護

隱私保護的數據發布沒有統一地衡量隱私泄露標準，常用屬性披露風險衡量隱私泄露。假設攻擊者的目標個體是r，準標識符屬性為QIr，則成功預測Sr的概率為Pr(Sr|QIr)。若攻擊者可以訪問發布數據集了解數據集每個屬性的取值域，由其他渠道獲得目標個體r（例如Alice）的QI值并且確定目標個體在已發布的數據集中，但不知道發布數據中的哪個記錄屬于目標個人。對數據發布者來說，可以選擇是否發布失真矩陣PBB或PMB，若數據發布者為了讓分析人員更有效地分析數據，則可以選擇發布失真矩陣PBB或PMB。

設πi=P[X=ci]，i=1，2，…，k，π=(π1，π2，…，πk)T，n表示數據集的個數，Ti表示原始數據集中值為ci的屬性個數，Si表示擾動數據集中值為ci的屬性個數，λi=P(Z=ci)，λ=(λ1，λ2，…，λk)T則有概率分布T=(T1，T2，…，Tk)T，S=(S1，S2，…，Sk)T，于是T～Mult(n，π)，S～Mult(n，λ)，此處λ=Pπ。需要注意的是數據發布者并不發布T1，T2，…，Tk，對數據分析者而言僅僅從擾動的數據無從得知它們，因此π的值不能直接求得，只能由T的觀察值S求得。如果P是非奇異矩陣，?是λ的無偏估計，則?是π的無偏估計。λ的最大似然估計是則有：

π的無偏估計方差為：

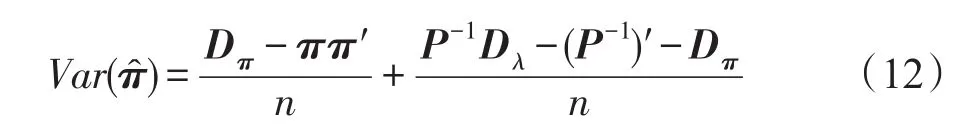
式中，Dπ是對角矩陣，其對角元素為π1，π2，…，πk，Dλ的定義與Dπ類似。等式（12）的右邊第一項是數據集固有方差，第二項是隨機化導致的額外附加方差。

3.4 隨機擾動的基本模式

數據集的屬性分為敏感屬性、準標識符屬性和其他屬性，攻擊者很容易根據原始數據集中準標識符屬性QIr推導出個體r的敏感屬性。為增加數據的不確定性、同時最大限度地保持數據效用，下面針對敏感屬性、準標識符屬性以及它們的組合討論隨機化問題。

敏感屬性隨機化（randomized response sensitive，RRS）：當數據所有者僅對敏感屬性隨機化時，攻擊者使用觀察到的敏感值和等式（4）估計其敏感值。正確估計的概率是那么敏感屬性披露風險為

這種情況針對攻擊者知曉用戶身份，有效保護用戶敏感信息，主要處理用戶身份不敏感的場合。

準標識符屬性隨機化（randomized response QI，RRQI）：當數據所有者僅對準標識符屬性進行隨機化時，正確重構QIr的概率由給出，因此敏感屬性披露的風險為其具體推導過程由下文等式（15）給出。

兩種屬性組合隨機化（randomized response both attributes，RRB）：當數據所有者同時隨機化QI和S時，攻擊者首先需要正確重構準標識符屬性值，其概率由給出，另外攻擊者還需要在正確重構準標識符屬性值以后重構敏感屬性值。這種隱私泄露情況與隨機化準標識符屬性類似，不再詳述。

下面對RRS、RRQI和RRB中敏感屬性披露風險進行總結，并給出隨機化屬性披露風險的一般計算：假設個體r具有準標識符屬性QIr=α={i1，i2，…，im}，ik∈Ωk，它的敏感屬性Sr=u，u∈ΩS。給定目標個體r的準標識符屬性值QIr，成功預測其敏感屬性值Sr的概率是：

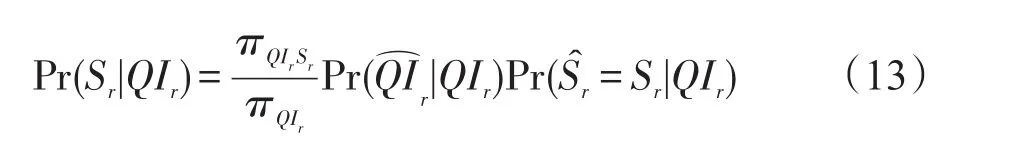
等式（13）中計算Pr(Sr|QIr)所需的重建概率表達式，其準標識符的重構概率由下式給出：

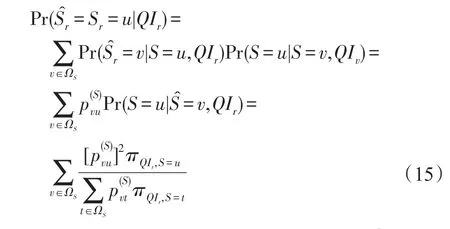
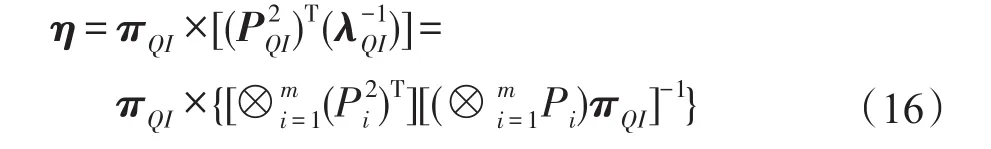
4 實驗評估

4.1 實驗設置

實驗采用UCI機器學習數據集，該數據集包含48 842個記錄的美國人口普查數據，共有14個屬性。此處選取 education、maritial-status、occupation、native-country、workclass這5個屬性，其中workclass作為敏感屬性，其余屬性作為準標識符屬性。實驗中利用KL-散度和χ2來測量原始敏感值分布和凈化數據集之間的距離，同時還驗證程序執行所需時間，檢驗數據量增長對運行時間的影響。為消除概率波動對實驗數據的影響，每個實驗運行11次，目的是驗證隨機化算法的穩定性。

4.2 實驗數據分析

一般情況下準標識符屬性和敏感屬性之間存在相關性，為減少相關性的干擾，在選取屬性值的時候進行了屬性相關性分析，選取的5個屬性相關性較小，即假設屬性之間具有獨立性。為表示方便，把本文的算法稱為RRPP（randomized respond to achieve privacy preserving）。

隱私保護數據發布的目的是最大限度地減少信息損失和最小限度地泄露隱私信息，為達到度量這兩方面的目的，此處使用KL-散度和χ2來度量原始數據和擾動數據之間的距離，其結果如表1、表2所示，其中表1是1次隨機響應運行結果，表2是10次運行取平均值的結果。原始數據和擾動數據之間的距離值越小，它們之間的差異越小，失真數據庫的效用越好。由表1和表2可以看到，在所有3個隨機化情景中，以KL-散度和χ2作為距離差異的效用損失在概率擾動和均勻擾動之間的差異（此處均勻擾動轉移概率取p=0.60，p=0.75，p=0.90）。表中數據顯示，采用RRPP方法比均勻擾動可以更有效地保留數據的效用，減少用戶信息的泄露。對均勻擾動來說，取p=0.90，攻擊者推測出用戶的敏感信息已經非常大了。另外，由表1和表2的平行數據對比中可以看出，算法的1次運行結果和10次運行結果的平均值差異很小，說明了算法較穩定。

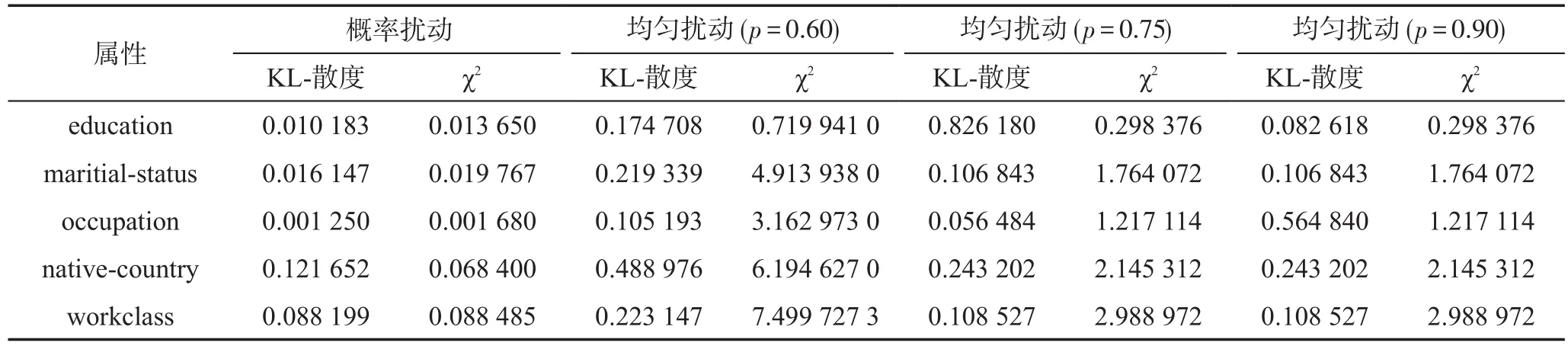
Table 1 Distance of original and perturbed dada(one time)表1 原始數據與擾動數據的距離（1次）

由于小概率事件可以視為不可能事件，這會導致采用RRPP算法擾動時發生屬性丟失現象。在后10次實驗中，有3次發生native-country屬性中Holand-Netherlands屬性值丟失，1次發生Ireland屬性值丟失。而采用均勻擾動p=0.60，p=0.75，p=0.90均沒有發生屬性值丟失現象。這可以解釋為RRPP算法對離群點具有一定的魯棒性。

Table 2 Distance of original and perturbed dada(ten times)表2 原始數據與擾動數據的距離（10次）

表3是RRPP與均勻擾動p=0.60，p=0.75，p=0.90的運行時間，該時間包括擾動、計算KL-散度、計算卡方的時間。之所以沒有把擾動的時間單獨測量，主要是為了驗證擾動和進行數據分析的時間是否可以接受。為了解算法的效率，采用執行10次算法取平均值的方式度量運行時間。對于RRPP算法其最小值為28.571 12 s，最大值為39.804 41 s。p=0.6時，運行時間的最小值為22.012 51 s，最大值為35.628 62 s，p=0.75和p=0.90其運行時間波動較小。由運行時間的對比可以看出，RRPP算法與均勻算法的運行時間處于同一個數量級。

Table 3 Running time ofAdult data set表3 Adult數據集運行時間 s

為驗證數據增長時擾動算法的有效性，針對每個屬性以增量的方式驗證其距離，橫軸表示增量，縱軸表示KL-散度和χ2，參與擾動的元組數分別為1 000、2 000、4 000、8 000、16 000、32 000，這些數據是均勻抽樣所得。屬性分別取敏感屬性workclass和準標識符屬性education（對所取的5個屬性都進行了驗證，由于篇幅關系，此處僅選取兩個屬性作為說明）。與驗證Adult數據集全部數據類似，執行算法11次，圖1（a）是敏感屬性值個數遞增workclass的KL-散度1次運行結果，圖1（b）是敏感屬性值個數遞增workclass的χ2距離1次運行結果；圖2（a）是敏感屬性值個數遞增workclass的KL-散度10次運行取平均值的結果，圖2（b）是敏感屬性值個數遞增workclass的χ2距離10次運行取平均值的結果。由圖1和圖2可以看出RRPP算法與均勻擾動p=0.90的結果相近，說明算法可以很好地保護用戶隱私和提供有效的數據效用。圖1的數據波動性較大，而10次運行結果取平均值則基本沒有大的數據波動。另外，無論RRPP算法還是均勻擾動在數據量較小時，其數據波動性較大，說明隨機響應方法需要用于數據量較大的場合。

Fig.1 Distance of workclass betweenπ andπ?(one time)圖1 敏感屬性workclass的π和π?之間的距離（1次）

Fig.2 Distance of workclass betweenπandπ?(ten times)圖2 敏感屬性workclass的π和π?之間的距離（10次）

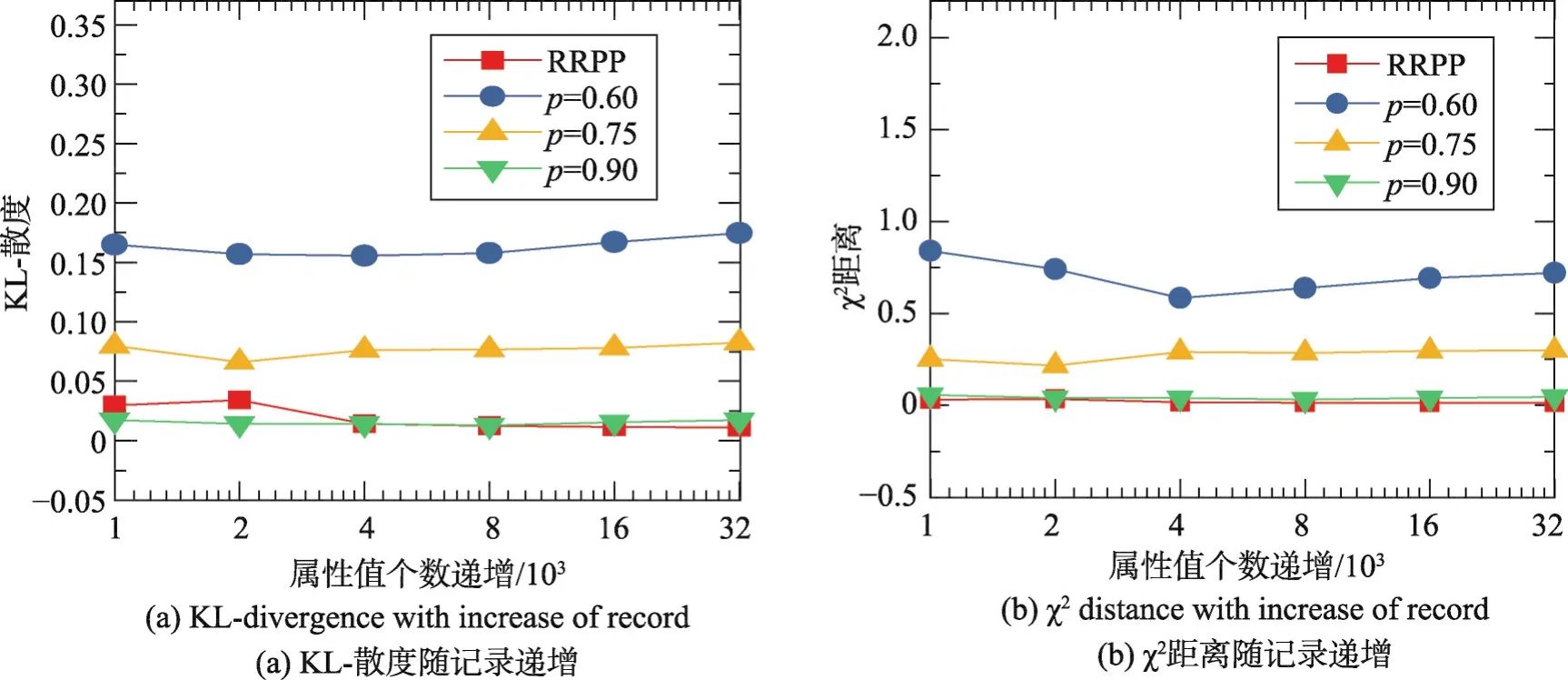
Fig.3 Distance of education betweenπandπ?(one time)圖3 準標識符屬性education的π和π?之間的距離（1次）

圖3（a）準標識符屬性education遞增時的KL-散度1次運行結果，圖3（b）是準標識符屬性education遞增時的χ2距離1次運行結果。圖4（a）準標識符屬性education遞增時的KL-散度10次運行結果，圖4（b）是準標識符屬性education遞增時的χ2距離10次運行結果。它們的結果與workclass基本相同。

由圖2和圖4可以看出，屬性不同，擾動數據與原始數據之間的KL-散度差別不大，而χ2距離卻比較明顯，比較圖2（b）和圖4（b），可以明顯看出敏感屬性workclass和準標識符屬性education的χ2距離有所差別。不過，無論KL-散度還是χ2距離，都在一個數量級。

由圖1至圖4可以看出敏感屬性個數的增加對KL-散度和χ2影響很小，特別是數據量達到2 000以后，基本上處于非常穩定的狀態。另外，在記錄很少的情況下有時會發生屬性值丟失現象，即對那些在總體中比率很小的屬性值在擾動時發生丟失。比如在增量實驗時，使用平均擾動方法，幾乎不發生屬性值丟失現象，因此離群點得以保留，這會導致離群點表示的用戶隱私泄露。而RRPP方法則可以剔除離群點的影響，在對native-country屬性進行擾動過程中發生了從少數國家或地區移民美國的公民其屬性值丟失（在數據量等于1 000時，屬性值丟失嚴重），被大概率的屬性值取代，這樣會導致數據失真，但是保持了用戶的隱私。

Fig.4 Distance of education betweenπ andπ?(ten times)圖4 準標識符屬性education的π和π?之間的距離（10次）

5 結束語

針對均勻擾動的隱私保護數據發布沒有考慮數據的原始分布問題，提出一種根據數據的原始分布對發布數據進行隨機擾動的方法，并詳細討論了二進制和多值屬性擾動矩陣參數設置，以及擾動矩陣滿足局部差分隱私的條件，最后設計實驗予以驗證，并對實驗結果進行討論。實驗結果表明，考慮數據原始概率情況下進行隨機化擾動顯著優于均勻擾動方法，相當于均勻擾動p=0.90的情況。實驗結果表明，基于數據原始分布的隨機化方法可以更好地保持原始數據集的分布特性，在數據效用和披露風險方面具有較好的效果。然而，文中還有不完美的地方，主要是假設數據屬性之間關系獨立性，實際上屬性之間存在千絲萬縷的聯系，下一步將對準標識符屬性之間存在強依賴關系時如何擾動進行研究，以更好地維持數據效用，保護用戶的隱私信息。