離散數據挖掘方法改進措施探究

石宜徑

（蘭州財經大學統計學院2016級應用統計專業，蘭州 730101）

數據挖掘就是從一系列龐大的數據體系中，通過采用一定的科學方法來獲得有用的信息，進而對我們的生產生活起到幫助作用。但是現實生活中，有諸多因素影響到數據的形成過程，采集過程。并且經過研究發現，諸多數據的屬性都具有極大連續性，即我們所說的連續屬性，因此將其進行離散化具有重要意義[1]。這就是數據的預處理，所以數據的預處理就是將所獲取的比較雜亂的數據經過信息提取，獲得有效信息的過程。我們都知道獲取的數據都具有連續屬性，對其進行離散化成為在數據挖掘之前非常重要的一步，這種操作對信息進行提取，不僅減小了數據量，使之經提取變成有用信息，而且還能提高數據模型的運行效率和結果優化，呈現更準確的數據結果。在名詞屬性中，大致可以分為三類：名詞屬性、數字屬性和連續值屬性。尤其注意的是，在數據處理過程中，大多數處理的是具有離散值屬性的數據集合，當然也有些既可以處理這些，也可以處理連續值屬性，這時候就出現一個問題，連續值屬性的處理結果會比離散值屬性結果差很多，因此我們要想獲得好的成果，就應該進行離散化處理，在這里我們應該注意離散化程度應該合理考慮數據情況與使用情況相結合，以達到處理的最佳結果。本文主要是對連續屬性數據離散化進行了解，分析自由度并提出改進算法，最后應用于實例中。

1 現狀

由于機器學習和數據挖掘技術的逐步深化，對連續屬性進行離散化越來越成熟，也有了很大的發展，但是到目前為止，仍然出現市場較為混亂，模型精度參差不齊，結果也不一。在1990年Chiu等人基于在離散化空間中提出熵最大的原理來形成的，就是在此空間中通過應該較為科學的搜索法來獲得較為合格的分區，尤其注意的是該算法需要西安選擇得到比較合適的初代分區，而該分區能夠影響后面的分類精度。隨后有科學家提出了基于信息熵的方法，涉及到了決策樹的引入，需要用到迭代回歸分析方法，為保證結果的有效性，需要在數據處理中引入前提條件，一般有這三種條件：最小信息增益、最小示例數和最大分區數。

到目前為止，研究學者主要對老舊算法進行了一定程度上的改進，相應也取得了顯著效果。比如說較為普遍的概率生成模型，該模型是依靠概率知識進行數據離散化，成果顯著提高[2]。其他有些方法是計算機工具提供的，較為死板，不值得提倡。對部分模型是經過其他專業領域經過直接采用所形成了，但很難被數據挖掘人員使用，不能很好普及。在這里值得一提的是基于粗糙集理論和布爾邏輯的屬性離散化方法，該方法的優點在于完全吸收了粗糙集理論的優勢與發揮布爾邏輯的優點，使得離散化結果更加具有可信性[3]。

2 基本原理

對數據進行離散化，就是依靠一些依據來對數據進行分類獲得所需結果。在生活中，最常見的就是按照學生的成績來進行劃分，分為不及格與及格學生名單。而又將及格名單可以進一步分為良好、優秀等不同區間。就比如依據年齡對人群進行劃分：兒童、少年、青年、中年、老年等。更遠的，還可以按照其他標準參數來劃分原始數據，例如身高、體重等等，相同的分類方式，不同的分類依據，也會得到不同的結果。

決策表定義為：設S=＜U，R，V，f＞為一信息系統，其中U={x1，x1，…，xn}是論域，A是屬性集合，V是屬性取值集合，F是U*A→V的映射。若A=C∪D，C∩D=?，C稱為條件屬性集，D稱為決策屬性集，則該信息系統稱為決策表。一個決策表S=＜U，R，V，f＞，其中R=C∪g0gggggg是總的屬性集合，子集C是條件屬性集，是決策屬性集，g0gggggg是決策屬性，U={x1，x1，…，xn}是論域。屬性a的值域Va上的一個斷點用（a，c）表示，其中c是實數集，a ∈ R。在值域 Va=[Ia,ra]上的任意斷點區間定義了V的一個分類pa：

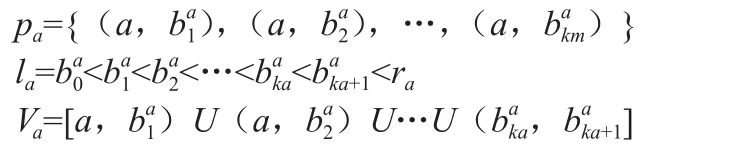
對于任意pa=Upa定義了新的決策表，SP=＜U，R，VP，f ＞fP其中xa∈U，i∈{0，1，…，Ka}，會形成新的信息。

屬性離散化的一般步驟如圖1所示：

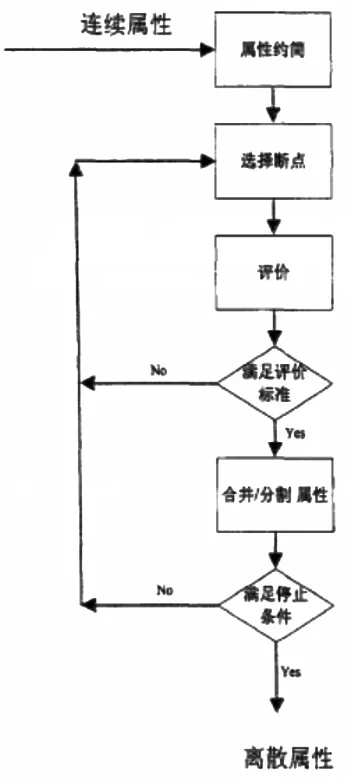
圖1 屬性離散化步驟

3 離散化算法

（1）等寬區間法。該方法是最簡單的算法，講的是數據按照等間隔劃分得到等間隔數列，最后每個數據的間隔都是相等的，但是對于離散卻隱約符合正態分布或其他分布的數據卻不太好。因為一般數據都趨向于某一數值，并且呈現出大量集中于某一塊或某一范圍的現象，對這種情況可以適當考慮等頻區間法。

（2）等頻區間法。這個算法的優點在于等頻，就是在區間內我們可以放入等多的數據，這些數據的數量是一樣多的，在一定上可以避免數據大量集中的問題，這個方法與上一個方法的區別在于，兩者都是等間隔，不同的是一個是等寬度，一個是等數量，兩者各有優劣，在具體使用中應該尤其注意。而且這兩種算法比較簡單，會使得處理結果較差，應該與其他高級算法結合，以達到所需效果。

（3）k-means算法。該算法比較常用，相對于上兩個算法，會更加高級與科學，尤其注意在算法運行前需要屬于分組個數。該算法的核心算法在于，先找到樣本的重心，然后以歐氏距離為依據來進行樣本劃分，然后重新計算重心再進行劃分，最后直到不再分類為止。在這里我們應該提前了解數據，對分類數量以及閾值有個設定，才能使分類結果更好。

4 基于自由度的離散化方法

4.1 卡方分布

χ2分布：設X1，X2，…Xn是來自總體N（0，1）的樣本，則稱統計量

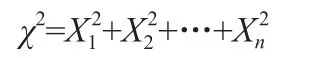
服從自由度為n的χ2分布，自由度指的是樣本個數。

4.2 Extended Chi2算法

Su等人在2005年提高了Modi fi ed Chi2算法，因為他認為原作者使用D的時候沒有考慮到實際分類過程中的差異，應該在獲得D的基礎上除以，來得到更為可靠的結果，即Extended Chi2算法[4]。該算法的步驟如下：

首先計算數據的不一致率，然后根據屬性值來進行升序排序處理，計算所有數據的χ2值，再結合具體的α數值來得到實際的Xα2數值，然后我們就可以得到D。然后執行迭代算法，當鄰區間不能再合并時結束循環，這時候再參考不一致率情況，如果不變則跳轉到計算D，否則進入下一步，即跳出迭代的合并。然后用新的α來代替舊值，算出D，并查閱是否可以將級，如果不能則跳出循環結束。最后，對所有屬性進行離散化，采用逐步運算方法，并參考不一致率。

5 基于改進自由度的離散化方法

在之前的算法中，我們是將自由度為k-1，對于上述算法。再后來的算法則是講自由度改為k′-1，而將k改為類別數。χ2分布的隨機變量：

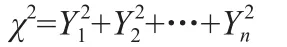
因此我們可以得出這樣的結論：自由度選取與類別數和相臨區間數是有關的，故而可以選2k-1作為自由度，k為系統的類別數。

6 結果驗證

UCI數據庫是加州大學歐文分校提出的用于機器學習的數據庫，這個數據庫暫時共有335個數據集，但還在增加。從該數據庫中隨機選取7個數據集進行驗證。如表1所示。

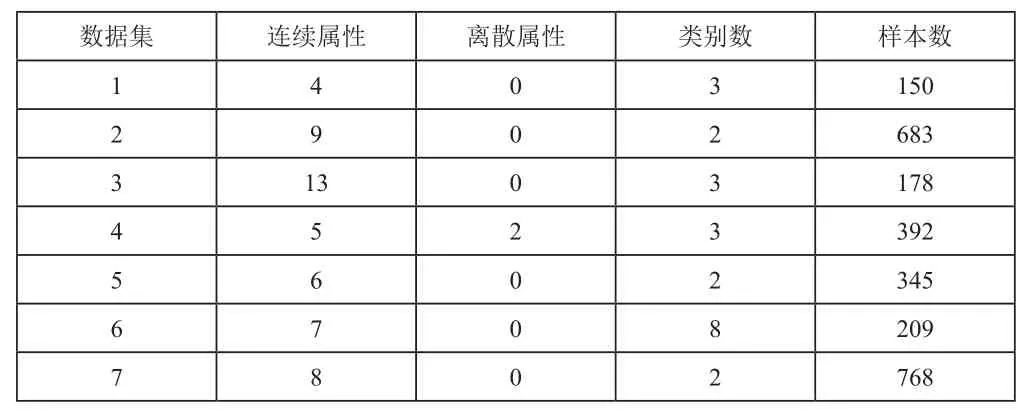
表1 數據集相關屬性統計表

對基本算法與改進算法用matlab進行編程，對7個數據進行處理（離散化），統計識別出正確識別率精度以及形成規則的平均個數，從表2中可以清楚看出，對于大多數數據，采用自由度改進算法進行處理，會使處理結果更好，說明改進算法有效。

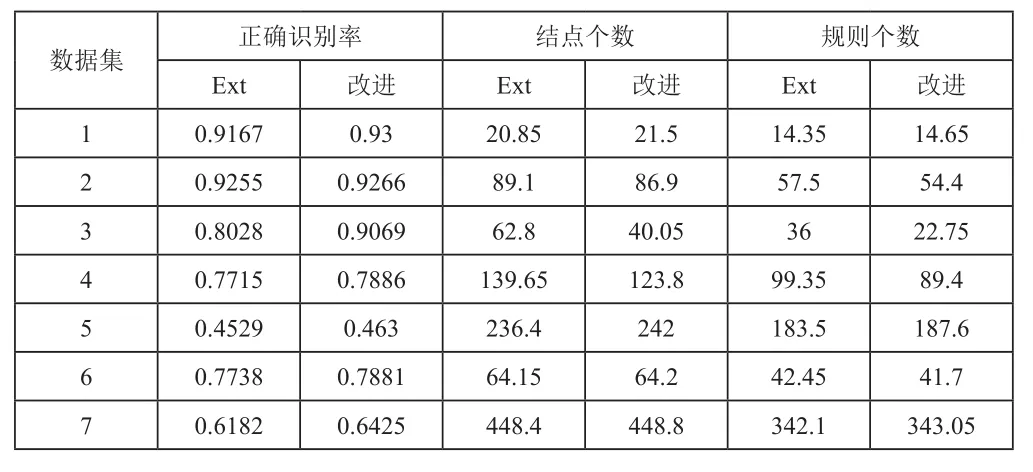
表2 處理結果表