激光星間鏈路終端指向誤差標定中的誤差分離研究

程竟爽，林益明，何善寶，王海紅，國愛燕

(1. 北京空間飛行器總體設計部，北京 100094；2. 中國空間技術研究院，北京 100094)

0 引 言

導航星座構建激光星間鏈路[1]時，激光星間鏈路終端(Laser Communications Terminal，LCT)會產生一定的指向誤差(即LCT出射光向量的理想指向與實際指向之間的偏差)，需要進行在軌標定[2]。在軌標定過程中，LCT指向誤差(測量數據)包含了航天器姿態測量誤差和LCT自身指向誤差的成分，航天器姿態測量誤差會影響LCT指向誤差標定結果的準確性。因此，開展LCT指向誤差在軌標定中航天器姿態測量誤差分離方法的研究具有重要意義。

目前，LCT指向誤差在軌標定方法[3]與星敏感器、慣性測量元件等設備在軌標定方法[4]類似，一般分為與航天器姿態有關的方法(如對地觀測法[5-7]、恒星觀測法[5,8]和鏈路觀測法[9-10]等)和與航天器姿態無關的方法(如終端自檢法[11])兩類。第一類方法是通過比較已知精確位置信息的信標光源(如地面信標光源、恒星光源與鏈路對方LCT信標光源等)位置觀測值與理論值之間的偏差，利用相應的估計方法估計LCT指向誤差參數。該類方法一般需要獲取高精度的航天器姿態測量信息，航天器姿態測量誤差會使得利用該類方法得到的LCT指向誤差參數標定結果偏離實際值；第二類方法則是依靠星上自檢光束，利用自檢光路標定LCT指向誤差參數。這類方法雖然克服了第一類方法中航天器姿態測量誤差影響LCT指向誤差標定結果的缺點，但只能對LCT內部的部分誤差參數進行標定，無法標定LCT外部安裝誤差等參數。文獻[12]結合鏈路觀測法和終端自檢法，提出了一種改進的LCT指向誤差在軌標定方法，但也沒有考慮航天器姿態測量誤差對LCT指向誤差標定結果的影響。文獻[13-15]針對包含測量設備自身偏差在內的航天器姿態估計問題，通過同時估計航天器姿態狀態、航天器姿態測量誤差與測量設備自身偏差參數，實現了航天器姿態測量誤差與測量設備自身偏差參數的分離。但上述方法中測量元件利用其大視場(如星敏感器)或多軸安裝(如慣性測量元件)的特點能夠同時獲取不同方向的測量數據，而LCT圖像傳感器受視場限制只能獲取單一方向的測量數據，因此該方法不能直接應用于有航天器姿態測量誤差時的LCT指向誤差在軌標定中。

針對上述問題，本文將開展航天器姿態測量誤差對LCT指向誤差標定結果的影響分析，在文獻[12]的基礎上提出基于多鏈路測量的航天器姿態測量誤差分離方法，利用導航星座中同一航天器建立多條鏈路的特點，同時估計航天器姿態測量誤差和LCT指向誤差參數，從而剔除(或降低)航天器姿態測量誤差對LCT指向誤差標定結果的影響，提高LCT指向誤差在軌標定結果的準確性。

1 LCT指向誤差標定基本原理與航天器姿態測量誤差對標定結果的影響分析

1.1 LCT指向誤差標定基本原理

tk時刻，航天器姿態向量θb,k，LCT的轉動角度向量θLCT,k和LCT入射光向量ur,k分別為

(1)

式中：θb,k,φb,k,ψb,k為航天器的姿態角，θg,k,φg,k,ψg,k分別為LCT粗指向機構的轉角，θs,k,φs,k,ψs,k分別為精指向機構的轉角,xr,k,yr,k和zr,k分別為ur,k在慣性系I-XiYiZi中的三軸分量。

如圖1所示[10]，LCT指向誤差標定時，入射光經粗指向機構平面反射鏡M和N、望遠鏡Te、精指向機構快速反射鏡S及光學中繼元件BS等構成的接收光路傳輸，在圖像傳感器F上形成光斑。

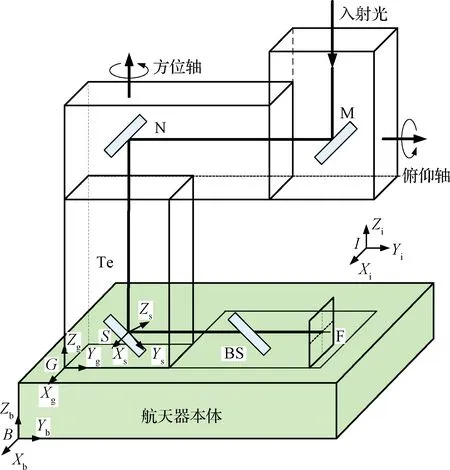
圖1 LCT接收光路與相應的坐標系Fig.1 Optical receive path in LCT and corresponding system coordinates

LCT存在基座、內部光學元件安裝誤差、軸系誤差、指向機構零位誤差等系統誤差，上述誤差統一記為參數形式的LCT指向誤差向量xLCT，即

xLCT=[Δxi, Δyi,Δzi]T

(2)

式中：Δxi,Δyi,Δzi分別為第i類誤差因素對應的三軸分量。xLCT可認為是常值向量。

依據文獻[12]中式(3),(4)給出的LCT指向誤差模型，光斑理想位置與實際位置的偏差向量l1,k為

l1,k=f(θb,k,θLCT,k,ur,k,xLCT)

(3)

式中:f=[f1,g1]T為l1,k與θb,k,θLCT,k,ur,k和xLCT之間的函數關系，f1,g1的含義參見文獻[12]。

(4)

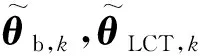
將式(4)代入式(3)中，得到

(5)

對式(5)進行展開并簡化，忽略高階項，得到

(6)

εk=HkXk+εk

(7)

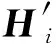
在軌標定經歷N次采樣，k=1,2,…,N，則整個采樣區間內對應的單鏈路測量方程組為

YN=HNX+E

(8)

式中：

若忽略Δθb,k,ΔθLCT,k和Δur,k，式(7)簡化為

(9)

類似，式(8)簡化為

(10)

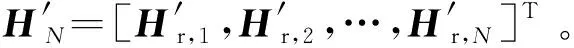
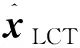
(11)

式中：W是指向誤差在軌數據的權值矩陣。

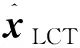
1.2 航天器姿態測量誤差對標定結果的影響分析

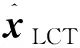
為了定量分析Δθb,k對xLCT標定結果的影響，進行如下的仿真，參數設置與仿真過程分別見本文3.1節與3.2節，LCT指向誤差標定結果如表1所示。(表中σθb為Δθb,k(假設服從零均值正態分布)的標準差，偏差為估計值與設定值之間的差值，最大偏差為同列偏差的最大絕對值。)

由表1可見，在給定的LCT指向誤差參數條件下，當σθb由20 μrad增大到200 μrad時，ε由10.4 μrad逐漸上升到164.0 μrad，即隨著航天器姿態測量誤差的增大，LCT指向誤差標定結果最大偏差逐漸增大，說明航天器姿態測量誤差對LCT指向誤差標定結果有著顯著影響，需要將航天器姿態測量誤差從LCT指向誤差測量數據中分離出去。

2 基于多鏈路測量的航天器姿態測量誤差分離

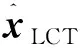
表1 不同航天器姿態測量誤差條件下LCT指向誤差標定結果Table 1 Estimation values of LCT pointing error parameters under different spacecraft’s attitude measurement errors

2.1 在軌標定源選擇

LCT指向誤差在軌標定一般選擇具有較強方向性的信標光源(如地面信標光源、恒星光源等)作為在軌標定源。基于國內導航星座星間鏈路距離在20 000～50 000 km、導航衛星定軌精度約為1～10 m，LCT入射光角度偏差(由航天器定軌誤差引起)約為0.02～0.5 μrad(經放大變換后仍小于LCT圖像傳感器的角分辨率)的技術現狀，選擇鏈路發送端的信標光源作為在軌標定源。

2.2 多鏈路測量方程組建立

估計LCT指向誤差參數時，待估計參數向量XN的維度nXN=3N+6，而測量方程組的秩rank≤2N，方程組虧秩，導致XN存在多個非平凡解。可見，由單一鏈路的測量數據無法同時估計航天器姿態測量誤差與LCT自身指向誤差參數。為此，本文引入多鏈路測量數據，建立多鏈路測量方程組。

設單一航天器搭載M臺LCT，每臺LCT與對方LCT建立一條鏈路，則將式(7)改寫為

(12)

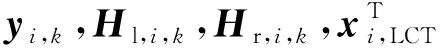
擴展式(12)，得到tk時刻的多鏈路測量方程組為

YM,k=HM,kXM,k+EM,k

(13)

擴展式(13)，整個采樣區間的多鏈路測量方程組

YMN=HMNX+EMN

(14)

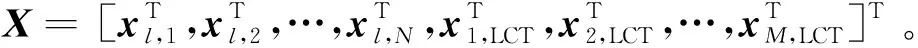
此時，由于X維度nX=nxLCT+nΔθb,k=3N+6M，而測量方程組的秩≤2MN。可以看出，式(10)利用了多條鏈路中航天器平臺姿態測量誤差的相關性，從而獲得了冗余的測量數據。

2.3 LCT指向誤差參數估計與誤差分離

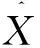
(15)

2.4 誤差分離前后的精度比較

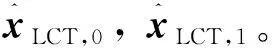
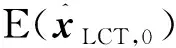
(16)

(17)

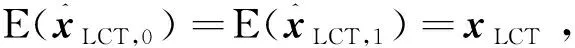
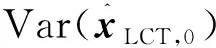
(18)

(19)

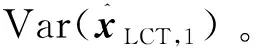
3 航天器姿態測量誤差分離方法有效性驗證

本節對航天器姿態測量誤差分離方法的有效性進行仿真驗證。

3.1 仿真工況參數設置

本文假設導航星座為Walker 24/3/1星座，該星座三個軌道面編號分別為A,B,C，星座構型如圖2所示。A軌道面內第一相位(編號為A1，其他編號以此類推)的衛星的軌道參數[17]如表2所示。導航星座內部構建激光星間鏈路網絡，依據星間鏈路建立約束條件[18]，其中部分衛星間可建立持續鏈路。

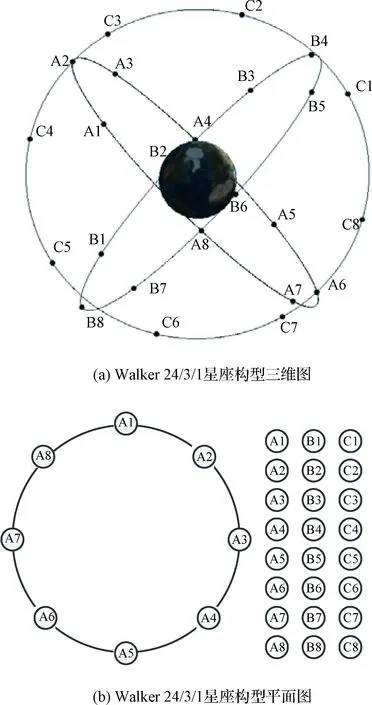
圖2 Walker 24/3/1星座構型Fig.2 Configuration of Walker 24/3/1 constellation

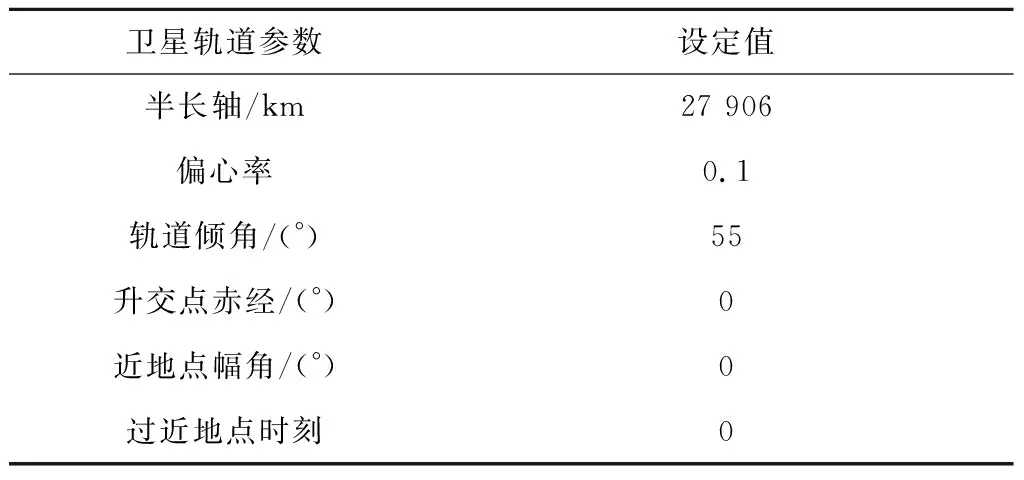
衛星軌道參數設定值半長軸/km27 906偏心率0.1軌道傾角/(°)55升交點赤經/(°)0近地點幅角/(°)0過近地點時刻0

考慮到導航衛星的特點，假設衛星本體僅做偏航運動。設置σθb分別為20、100和200 μrad。各LCT的安裝形式使得LCT基座坐標系G-XgYgZg與航天器本體坐標系B-XbYbZb保持一致，LCT指向誤差參數設置[9]如表3所示。望遠鏡放大倍率m=20。

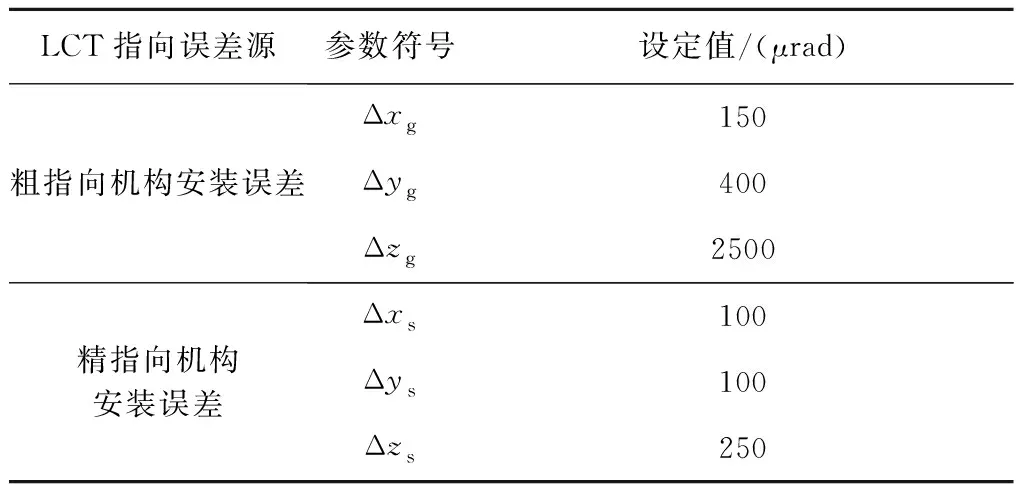
表3 LCT指向誤差參數設置Table 3 Settings of LCT pointing error parameters

3.2 仿真過程

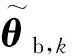
(20)

具體仿真結果見表1。

3.3 航天器姿態測量誤差分離方法有效性驗證

設σθb=100 μrad，依據提出的航天器姿態測量誤差分離方法，獲取不同鏈路的觀測數據，計算得到各參數的估計值，比較分離前后的ε。若分離后的ε更小，說明航天器姿態測量誤差分離方

法有效。

1)鏈路條數

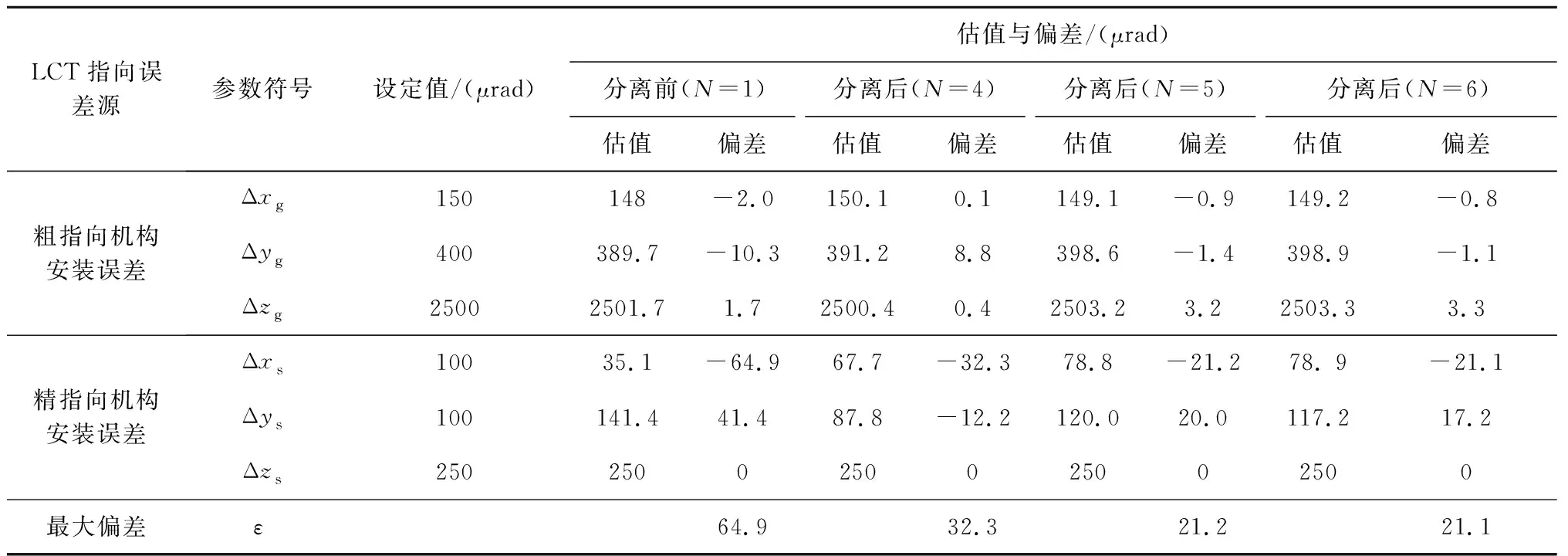
表4 不同鏈路條數條件下LCT指向誤差標定結果Table 4 Estimation values of LCT pointing error parameters with measurements from different number of links

2)鏈路拓撲構型

以4條鏈路為例，按照原則：1)鏈路拓撲構型包含2條同軌鏈路和2條異軌鏈路；2)鏈路拓撲構型盡可能對稱，依據鏈路建立約束條件設計10種鏈路拓撲構型。其中構型1和構型6如圖3所示。

構型1和構型6條件下，估計結果分別如圖4和圖5所示，圖中Δθb,x, Δθb,y與Δθb,z分別表示航天器姿態測量誤差沿X，Y與Z軸的分量。

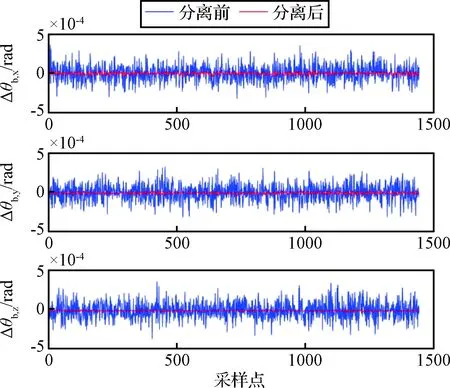
圖3 拓撲1構型條件下航天器姿態測量誤差估計結果Fig.3 Estimation results of spacecraft attitude measurement error with topology No.1

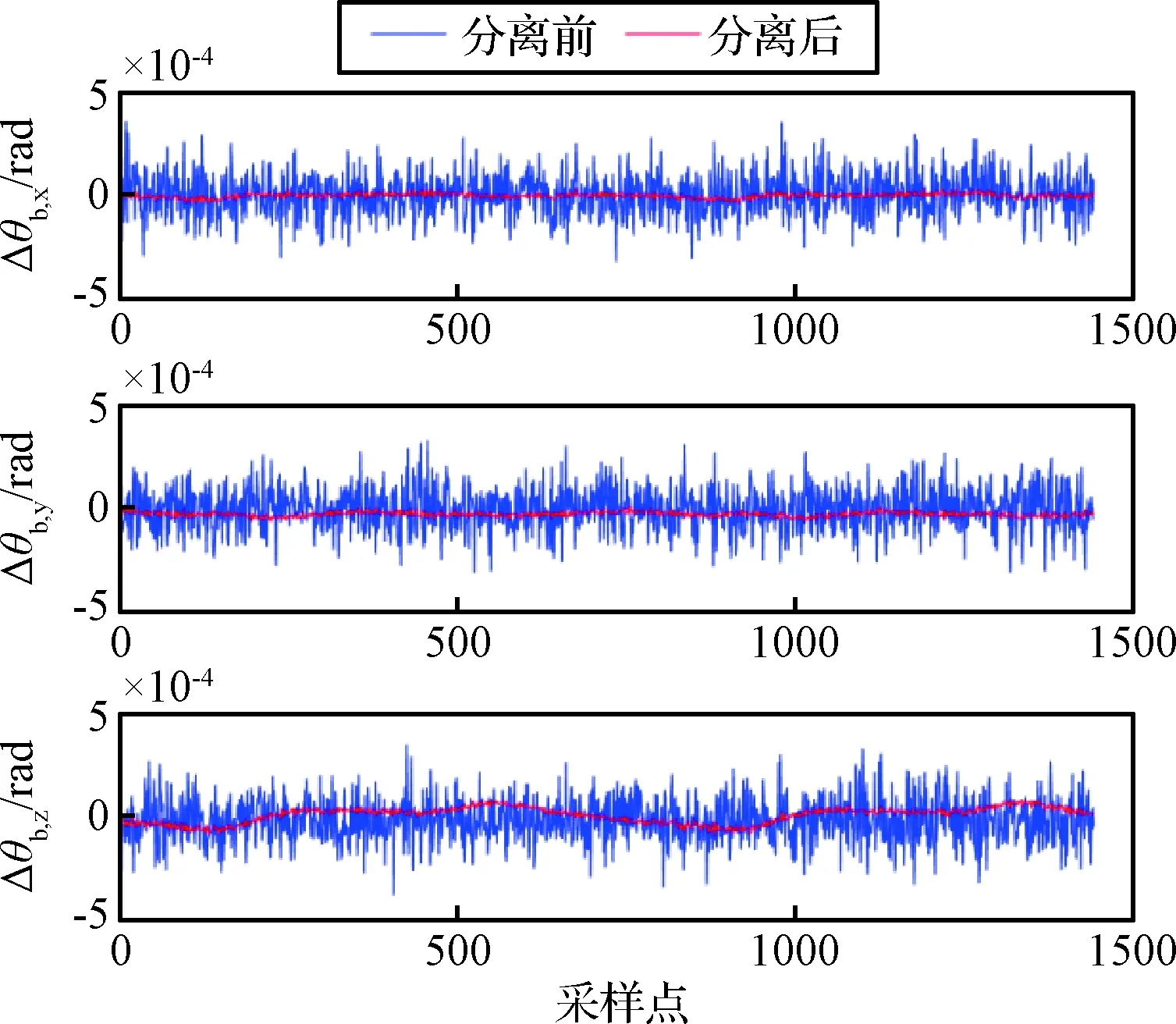
圖4 拓撲6構型條件下航天器姿態測量誤差估計結果Fig.4 Estimation results of spacecraft attitude measurement error with topology No.6

4 結 論

1)航天器姿態測量誤差對LCT指向誤差標定

結果有顯著影響。隨著航天器平臺姿態測量誤差的增大，LCT指向誤差標定結果最大偏差逐漸增大。當航天器姿態測量誤差由σθb=20 μrad增大到σθb=200 μrad時，LCT指向誤差標定結果最大偏差由10.4 μrad逐漸上升到164.0 μrad。

2)本文提出的基于多鏈路測量的航天器姿態測量誤差分離方法能夠有效降低航天器姿態測量誤差對LCT指向誤差標定結果的影響。具體表現為：LCT指向誤差標定結果最大偏差由誤差分離前的64.9 μrad下降到誤差分離(6條鏈路)后的21.1 μrad。

3)該誤差分離方法的有效性取決于鏈路條數和鏈路拓撲構型。鏈路條數增加，LCT指向誤差標定結果最大偏差逐漸下降。建議采用5到6條鏈路(至少2條鏈路)進行誤差分離。在確定鏈路條數后，應依據鏈路建立約束條件，在可用的鏈路拓撲構型中優選出適用的拓撲構型。

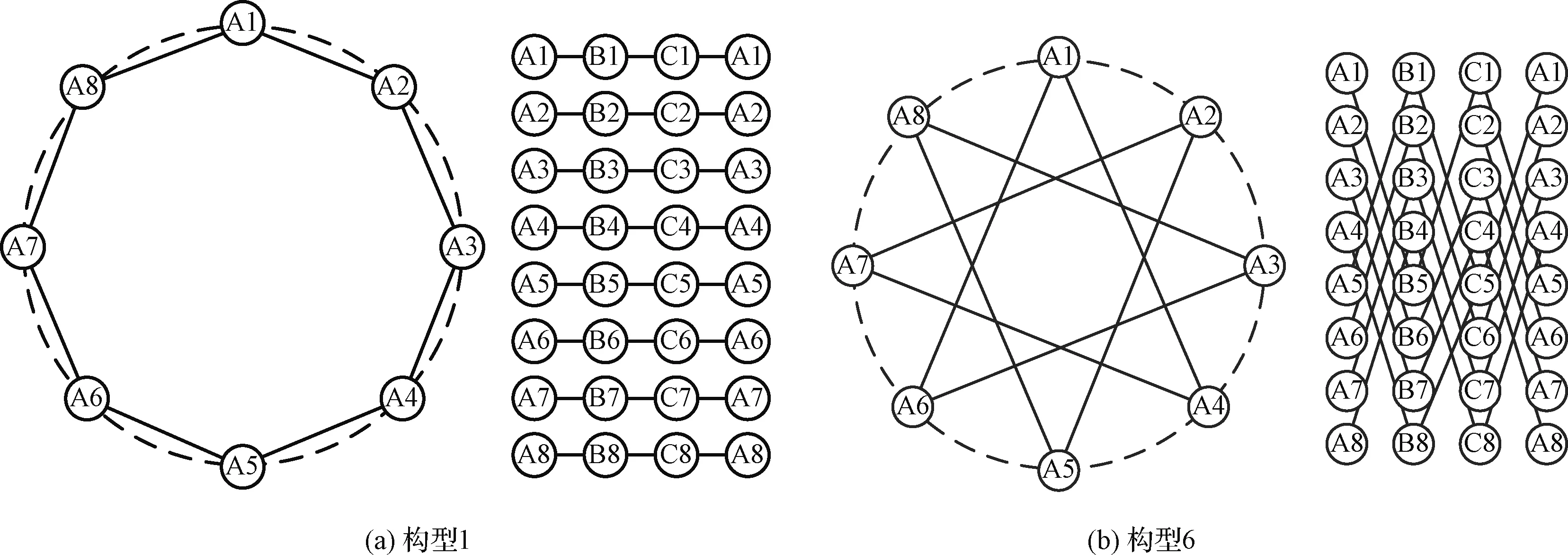
圖5 鏈路拓撲構型1和6(4條鏈路)Fig.5 Link topologies 1 and 6(4 links)

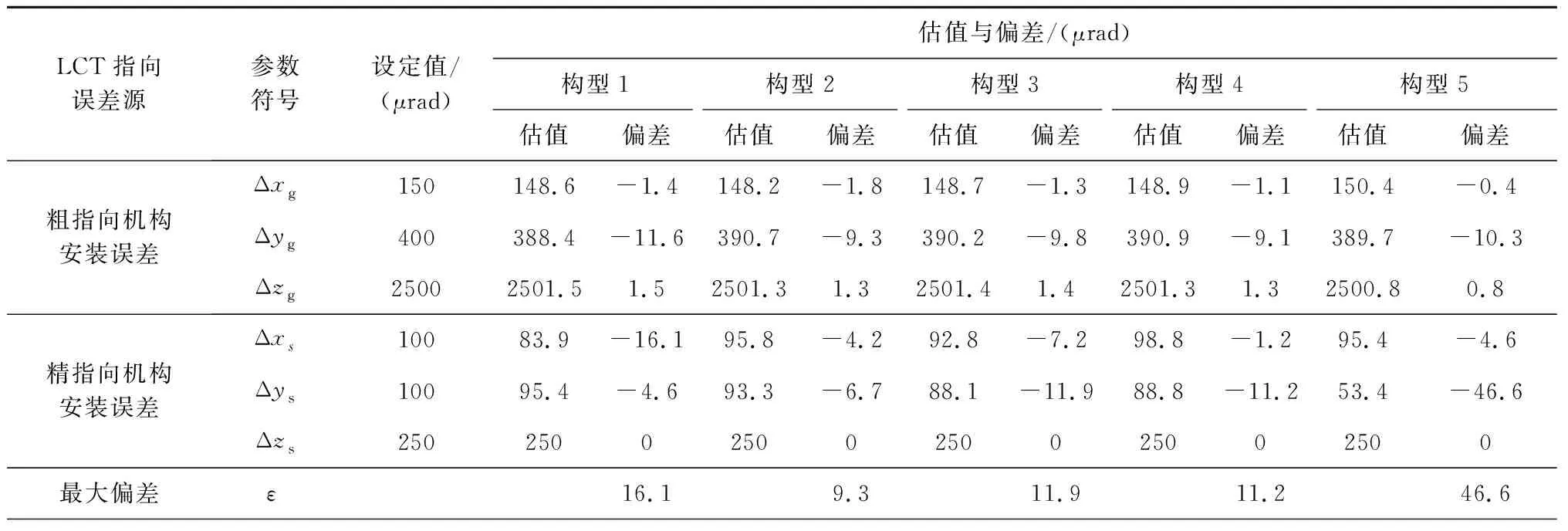
LCT指向誤差源參數符號設定值/(μrad)估值與偏差/(μrad)構型1構型2構型3構型4構型5估值偏差估值偏差估值偏差估值偏差估值偏差粗指向機構安裝誤差Δxg150148.6-1.4148.2-1.8148.7-1.3148.9-1.1150.4-0.4Δyg400388.4-11.6390.7-9.3390.2-9.8390.9-9.1389.7-10.3Δzg25002501.51.52501.31.32501.41.42501.31.32500.80.8精指向機構安裝誤差Δxs10083.9-16.195.8-4.292.8-7.298.8-1.295.4-4.6Δys10095.4-4.693.3-6.788.1-11.988.8-11.253.4-46.6Δzs25025002500250025002500最大偏差ε16.19.311.911.246.6

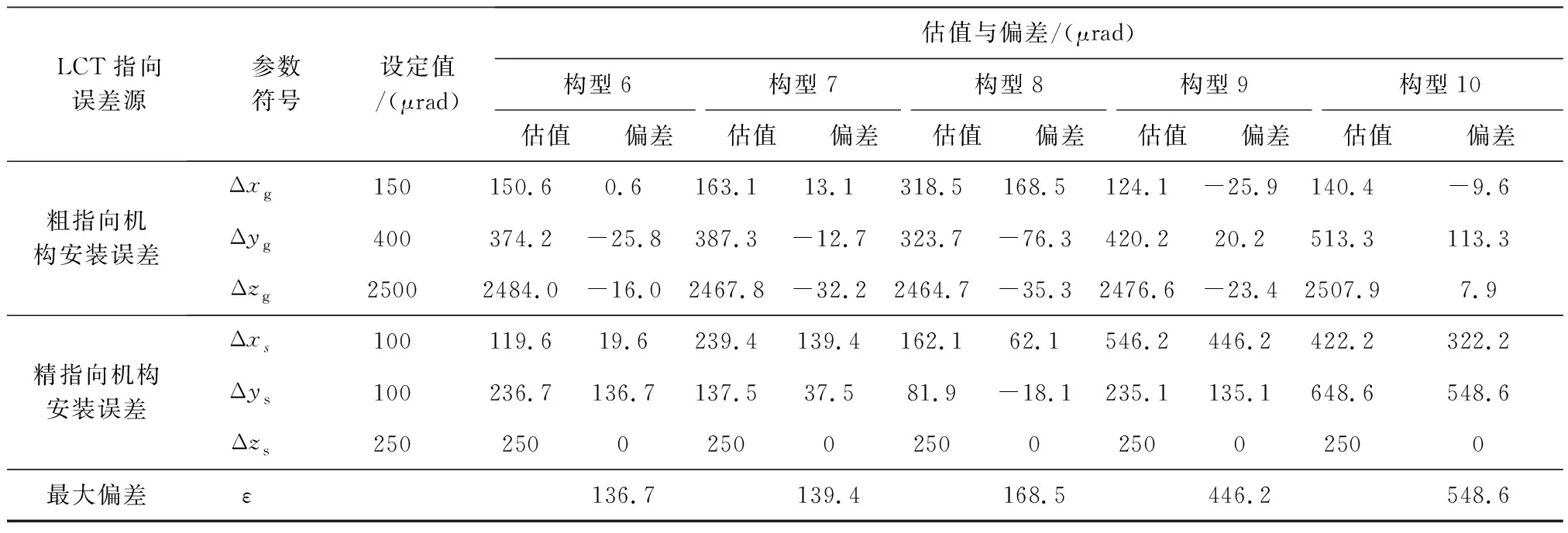
續表