產品族架構設計與供應商選擇的主從關聯優化

杜 綱 關進良 熊奕璇 馬玉潔

天津大學管理與經濟學部，天津，300072

0 引言

隨著市場多樣化和個性化需求的發展，企業面臨著巨大的挑戰，需要在控制成本的前提下迎合不同市場中的顧客需求，因此，產品族已經成為企業產品開發的基本單元[1]。供應商是構成企業競爭力的一個必不可少的要素，供應商的選擇也直接影響著供應鏈的整體性、連續性和協調性。供應商的供貨能力、所提供的物料質量等直接影響所制造產品的質量，以及企業的效益，從而對企業競爭力造成影響[2]。目前有關產品族設計與供應商選擇的研究較多，且理論體系逐漸成熟，但大部分有關產品族設計與供應商選擇的文獻都是定性分析，相關的定量分析文章相對較少，且大部分研究只考慮單一環境中產品族設計與供應商選擇的優化[3-5]，極少將兩者聯合考慮進行優化。客車底盤是具有模塊化特性的產品，牛連防[6]從技術、經濟和社會3個指標方面構建了底盤產品族的評價指標體系，并認為底盤產品族的模塊選擇與供應商有很大聯系。DU等[7]采用通用產品結構來描述產品族中具有層次結構的模塊組織、模塊實例與產品變形，并開發不同的變異或衍生產品來滿足不同的市場需求。ZHANG等[8]考慮模塊選擇和供應商的選擇，建立整合平臺產品設計和物料購買決策的混合線性規劃模型。LUO等[9]對模塊選擇和供應商選擇進行研究，建立了單層優化模型。CAO等[10]針對供應商設計階段進行研究，探討基于平臺的產品供應商預選擇，最小化外包成本和供應商風險。

上述優化方案忽略了兩種不同決策問題之間的協調，只是簡單地將產品問題與供應商選擇問題進行線性結合，實際上產品族配置與供應商選擇在決策主體、目標等方面是一個主從關聯的協調設計與優化問題，兩者在研究過程中并不是彼此獨立的，而是相互影響和關聯的。供應商的選擇一般要服從產品族的整體利益，而產品族中的架構設計對下層供應商的相關因素具有影響和約束，進而影響整個供應商的選擇[11]。

目前，許多學者研究了供應商評價的多種準則。馬士華等[12]在參閱國外相關研究文獻的基礎上，提出企業業績、生產能力、質量和企業環境等四項一級指標的供應鏈合作伙伴評價體系。為了使風險降到最低，朱兵[13]結合質量系統、環境、績效等指標建立評價系統對供應商進行選擇。侯萍[14]對電商企業的電子采購過程進行了研究，確定由質量、績效、服務、環境等指標構成的供應商評價體系。劉曉等[15]采用分類的方法，深入分析推式采購和拉式采購環境下的供應商選擇模型與方法。上述研究都只考慮供應鏈中的因素來確定供應商選擇指標，并未結合產品族設計來考慮供應商選擇。

雙層規劃是指模型的約束中包含子優化問題的數學規劃[16]，雙層規劃雖然可以作為數學規劃的一種推廣形式，但它與普通數學規劃有著很大的不同，由于其模型的上層中含有下層的最優解或最優值函數，使得模型成為一個非光滑的優化問題，并且當上層的約束中含有下層的最優解時其可行域可能是不連通的。目前雙層規劃被應用在不同的領域，但將雙層優化的模型與方法應用于產品族優化設計的研究仍較少。

本文在已有研究的基礎上，將產品族模塊架構設計和供應商的選擇分別作為主、從規劃問題，構建了一個雙層規劃模型并提出了包括優化模型、計算求解等在內的一整套關聯優化方法，并將該方法應用于某汽車底盤產品族架構設計及供應商選擇的案例中。

1 問題描述

本文將產品族架構設計與供應商選擇進行協同優化，最大化制造商的利益。產品族架構設計與供應商選擇問題就是產品空間決策問題與供應鏈空間決策問題。由于產品族架構設計是產品族設計的前端環節，在時間順序及層次上位于供應商選擇的前一層次，并且產品族架構設計的結果將作為供應商選擇的輸入，供應商選擇的結果又是對產品族架構設計的評價，故兩者是一個具有主從關系的關聯優化問題，其中產品族架構為主，供應商選擇為從。產品由通用模塊和可選模塊組成，每個可選模塊都有各自的模塊候選項，每個模塊候選項對應不同的供應商。根據模塊功能和效用的不同，由多個基本模塊組成的模塊為復合模塊。供應商選擇方案為從供應商集合中選擇合適的供應商來供應產品族的可選模塊，見圖1。

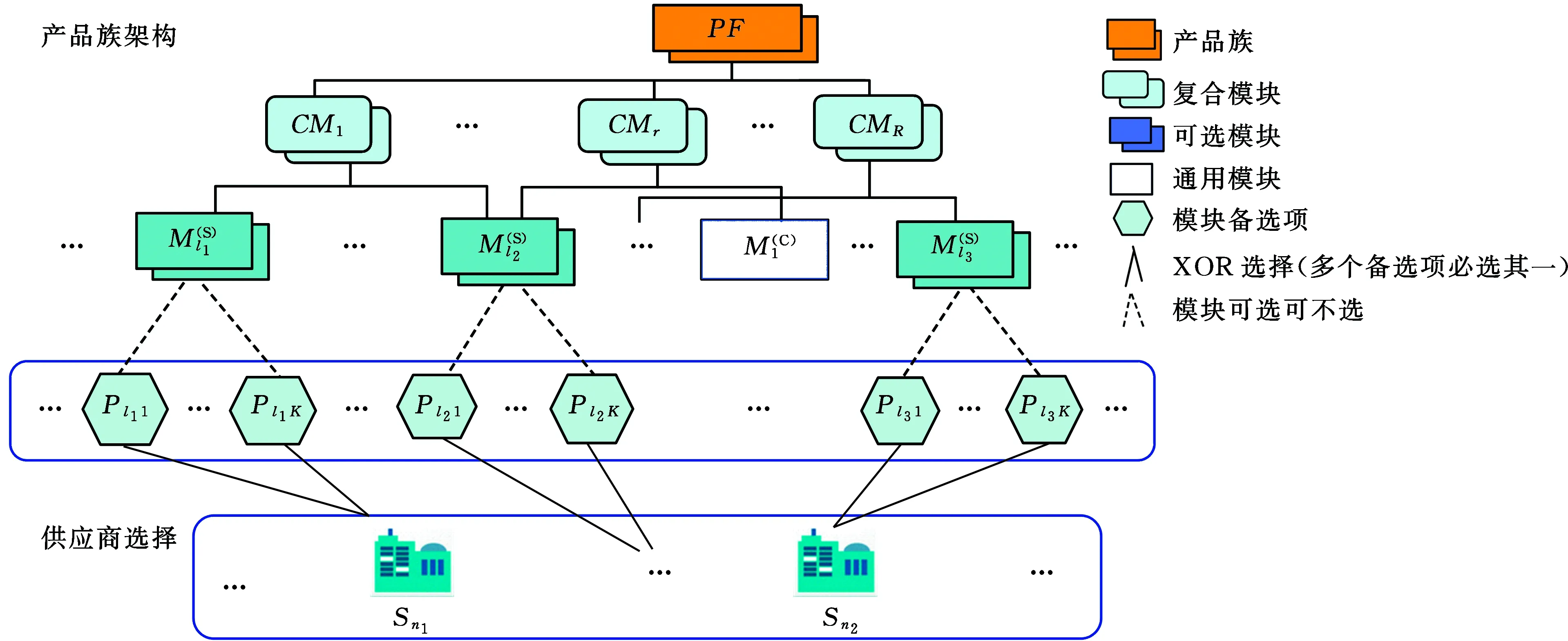
圖1 問題圖Fig.1 Problem diagram

在此協同優化問題中，已知產品族的所有基本模塊集合{1,2,…,k,…，K}和對應的模塊備選項集合{1,2，…,lk,…,Lk}，以及這些模塊備選項的功能效用uikl。基本模塊分為通用模塊和可選模塊，通用模塊是構成產品族產品平臺的必要元素，可選模塊是形成產品族差異化的元素。通用模塊集合和可選模塊集合的信息已知。優化模型模塊的一般形式記為mk，k∈{1,2，…,K}，每種模塊mk有lk個候選項，則第k種模塊的第l個候選項表示為mkl。產品族架構設計問題也可以描述為在所有模塊組合中進行選擇，組合成不同的產品變形問題。產品變形的集合為P(P={Pj,j=1,2，…,J})。針對供應商選擇問題，已知供應商的集合{1,2，…，s,…,S}，以及制造商將零件交給供應商進行生產的固定投資、模塊的采購成本及風險成本。根據產品的模塊選擇決策來判斷哪些模塊由哪些供應商提供。

1.1 變量與參數

基于以上對問題的分析和決策機制，根據Stackelberg理論構建雙層主從關聯優化模型，并對模型的上層和下層構建及模型的主從關聯進行分析和研究[17]。其中產品架構設計扮演領導者的角色，供應商的選擇扮演跟隨者的角色。本文所涉及的參數如下。

(1)集合包括市場的種類I、產品的種類J、基本模塊的種類K、模塊備選項的種類L、供應商的種類S。

(2)決策變量包括xjrkl、ykls。xjrkl表示第j個產品變形的第r個復合模塊是否選擇第k個基本模塊的第l個模塊備選項，ykls表示供應商s提供模塊k的備選項l。

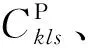
產品族架構的目標是極大化效用與成本比值，決策產品族的模塊選擇。記X={X1,…,Xj,…，XJ}={…,xjr,…,xjR,…}={…,xjr1,…,xjrK,…}={…,xjrk1,…,xjrkL,…}，上層決策變量為xjrkl。下層供應商選擇受上層產品族架構方案的約束，需要決策由哪個供應商來提供可選模塊。圖2所示為主從規劃模型的決策變量結構。上層根據已知信息選擇模塊，對產品族架構設計進行優化，下層根據上層傳遞下來的變量xjrkl選擇相應的供應商，對總成本進行優化，并將優化結果ykls反饋給上層。

1.2 上層

模型的上層是對產品族架構進行優化，求產品族設計方案。上層的目標函數是表示配置決策的依據，也是對配置決策的一種評價。評價最基本的準則是客戶利益和企業利益的極大化，這是由企業發展產品族的根本目的所決定的[18]。本文將單位成本效用作為產品族配置的優化目標。客戶利益是指客戶認為產品對自己核心需求的貢獻和滿足程度,本文采用客戶認為的產品效用Uij來表示。為便于度量，將Uij分解為如下來自客戶認為各模塊的綜合效用：

(1)

式中，wjk為第k個模塊在產品變形Pj中的權重。

上層模型表達為

(2)

(3)

xjrkl≥xjrklRkk′

(4)

r∈{1,2，…,R};k,k′∈{1,2，…,K}

(5)

(6)

(7)

R∈N+xjrkl∈{0,1}

(8)

式中，C為總成本；Rkk′為制造基本模塊k和基本模塊k′的耦合系數。

顧客選擇產品受到自身、外界環境等各種因素的影響，式(3)表示細分市場i中產品j被顧客選擇的概率，可由客戶效用的概率選擇規則(MNL)方法計算得到。產品族架構設計約束根據工程經濟學和邏輯性約束來建立，如產品族中模塊制造、組裝的關聯約束。式(4)表示有關聯的模塊必須組裝到同一復合模塊中。式(5)表示產品差異性，確保不同的產品有不同的模塊組成方式。式(6)確保每個產品復合模塊中的基本模塊的模塊備選項不重復。式(7)表示每個基本模塊只能選擇一個備選項或者不被選擇。式(8)表示決策變量的邏輯約束。

1.3 下層

模型上層決策產品族架構，決定每個產品變形的模塊配置選擇xjrkl，并將xjrkl傳遞給下層。下層的目標函數是供應商的總成本，總成本包括固定成本、供應商采購成本和風險成本。下層將決策結果反饋給上層，根據最終成本來影響上層產品族架構設計決策，總成本C是極小化目標，即

minC(xjrkl,ykls)=CF+CM+CR

(9)

(10)

(11)

式中，CF為固定成本；CM為供應商的供貨成本；CR為供應商的風險成本。

下層約束主要為邏輯約束：

(12)

ykls∈{0,1}

(13)

式中，Njks為每個供應商s提供模塊k的備選項l的量；Ns為供應商的供貨能力。

式(12)為供應商供貨能力約束，每個供應商s提供模塊k的備選項l的量的總和不超過自身的供貨能力。式(13)表示決策變量在0和1之間取值。

1.4 整合優化模型

基于上下層模型，可以建立產品族架構設計與供應商選擇關聯優化的雙層規劃模型：

(14)

minC(X,Y)=CF+CM+CR

(15)

其中上下層各自一些兼容性約束將在案例分析中根據實際情況給出。式(14)的約束條件為式(4)～式(8)，式(15)的約束條件為式(12)、式(13)。

產品族架構設計和供應商選擇的聯合優化問題可作為一個主從優化模型進行建模，產品族架構設計優化為主，供應商選擇為從。產品族架構設計是對變形產品選擇、模塊選擇和基本備選項選擇進行決策，也就是確定決策變量xjrkl。供應商決策就是將產品Pj的成本反饋給上層，即下層將最優成本C反饋給上層，影響上層的綜合效用。模型經計算得到最優解(X*,Y*)，即最優產品族架構方案和供應商選擇方案。

2 模型求解

2.1 算法構建

雙層模型求解方法可分為直接方法和間接方法兩類。直接方法是依據雙層規劃的決策機制直接求解，首先由上層模型的優化目標求出一個解，同時下層以該解中的上層變量為參變量求解下層模型，采用某種優化規則進行迭代，直至得到最優解。間接方法是在一定條件下將模型先轉化為等價的單層問題，然后通過求解單層問題得到雙層規劃的解。轉化為單層的主要方法是當下層每個模型都是一個凸規劃時，將下層問題由其KKT條件代替。由于模型是一個規模較大的0-1非線性規劃問題，為使所構建的遺傳算法具有全局收斂性，本文構建了雙層嵌套遺傳算法，利用外層遺傳算法求解上層問題，將上層問題的決策變量X*傳遞給下層，內層遺傳算法以此為參數進行求解，然后將求解出的下層問題最優結果Y*返回給上層進行迭代。

2.2 求解過程

2.2.1變量處理

為縮小搜索空間和保持染色體中片段對約束的滿足優勢，需對算法編碼和算子進行設置。

(1)編碼選擇。遺傳算法的實現基礎是將待解決的問題表示為一個有限長度的串，稱為染色體。基于雙層決策模型，本文采用嵌套式遺傳算法，編碼分為上層(ULC)與下層(LLC)兩部分，且上下層染色體都對應于各自的解X和Y。圖3給出了上層問題的染色體編碼，上層問題染色體的長度就是模塊備選項的總數，為J×R×K×L，染色體中的每個基因代表一個模塊備選項。根據上層的結果，每條染色體對應一個基本模塊，每個基因代表基本模塊所對應的模塊備選項的選擇。下層問題染色體長度為K×L×S，每個基因表示對應每個產品的供應商，具體編碼見圖4。

(2)交叉與變異。染色體間要在一定的約束下完成交叉與變異。遺傳算法中的交叉是指任意選擇兩個父代染色體以一定的概率交換他們其中的一部分基因。當一對染色體被選擇后，他們各自將會隨機產生兩個交叉點，同時交換的范圍也被確定，通過交換選擇的染色體的片段得到子代染色體。變異出現在交叉之后，并作用于獨立的后代，它以小概率隨機挑選一個基因，并且改變其模塊實例。

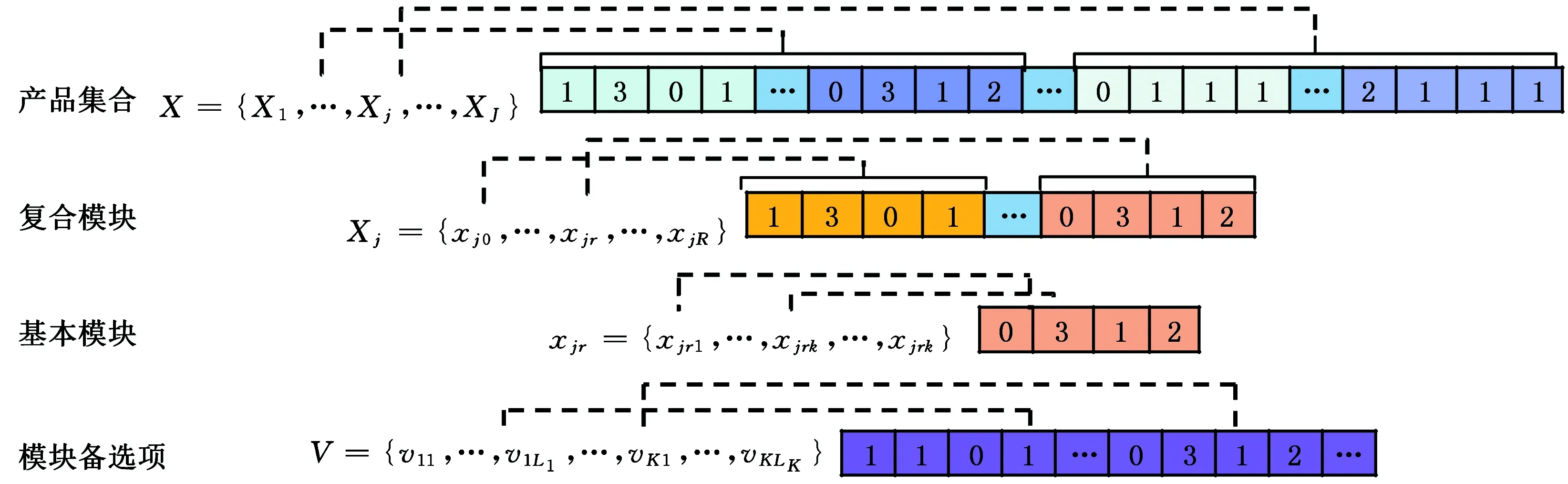
圖3 上層變量編碼示例Fig.3 Example of upper-level variable encoding

圖4 下層變量編碼示例Fig.4 Example of lower-level variable encoding

2.2.2求解流程

產品族架構設計優化與供應商選擇問題主從關聯優化模型是一個0-1非線性雙層整數規劃模型。基于上節分析，本文構建了一個嵌套遺傳算法用于解決這類雙層規劃問題，具體求解流程見圖5。

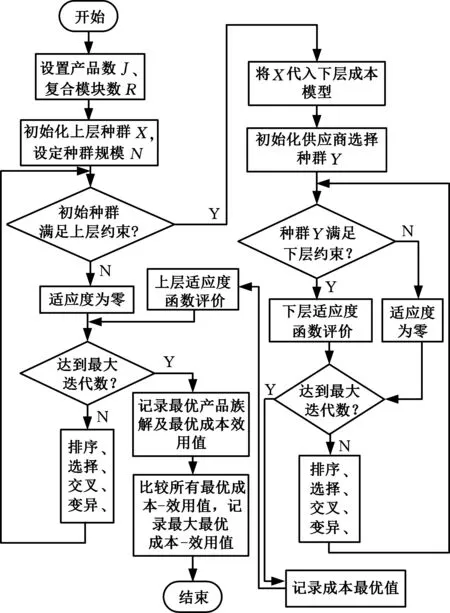
圖5 遺傳算法流程圖Fig.5 Genetic algorithm flow chart

(1)確定產品數J和復合模塊數R，并初始化種群。根據上層變量規模隨機生成種群規模N，且滿足邊界約束。

(2)判斷種群是否滿足上層約束，若滿足，則代入下層，若不滿足，則將適應度設為零，轉下一步。

(3)上層判斷種群是否達到最大代數，若已達到最大代數，則記錄最優值，轉入下一步，若未達到最大代數，則進入排序、選擇、交叉與變異過程，之后再進入步驟(2)，重復。

(4)下層將上層可行個體代入并初始化生成下層種群Y，下層驗證種群可行性，若滿足則進行適應度評價，若不滿足則將適應度設為零。

(5)判斷下層種群是否達到最大代數，若達到則記錄下層最優個體與最優值，若未達到則返回步驟(4)并重復至最大代數。

(6)將下層最優個體與最優值代入上層計算效用比成本值，并進行適應度值評價。

(7)判斷種群是否達到最大代數，達到則記錄最優解與最優值，未達到則重復步驟(3)直至最大代數。

(8)記錄上層最優解與最優值后判斷模塊數是否取完所有可行值，若取完則結束，若沒取完則返回步驟(1)，重復。

3 案例研究

3.1 背景介紹

以某品牌客車為例介紹本文優化模型的應用求解。根據實際調研及資料查閱，選取了底盤的主要部件，忽略部分部件，如變速箱和傳動軸。將客車的底盤分為發動機、傳動系統、行駛系統、轉向系統和制動系統五部分，這五個部分又分為機體組、供給系統等細分模塊,并將這些基本模塊分為通用模塊和可選模塊。客車底盤模塊結構見圖6。

基本模塊的效用和成本等信息見表1。本文只考慮一個主要的目標市場，也就是I=1，市場規模Q=20 000。供應商s提供模塊k的備選項l發生風險的概率rkls通過給出的供應商在不同可選模塊中各模塊候選項的供貨可靠性值來確定。

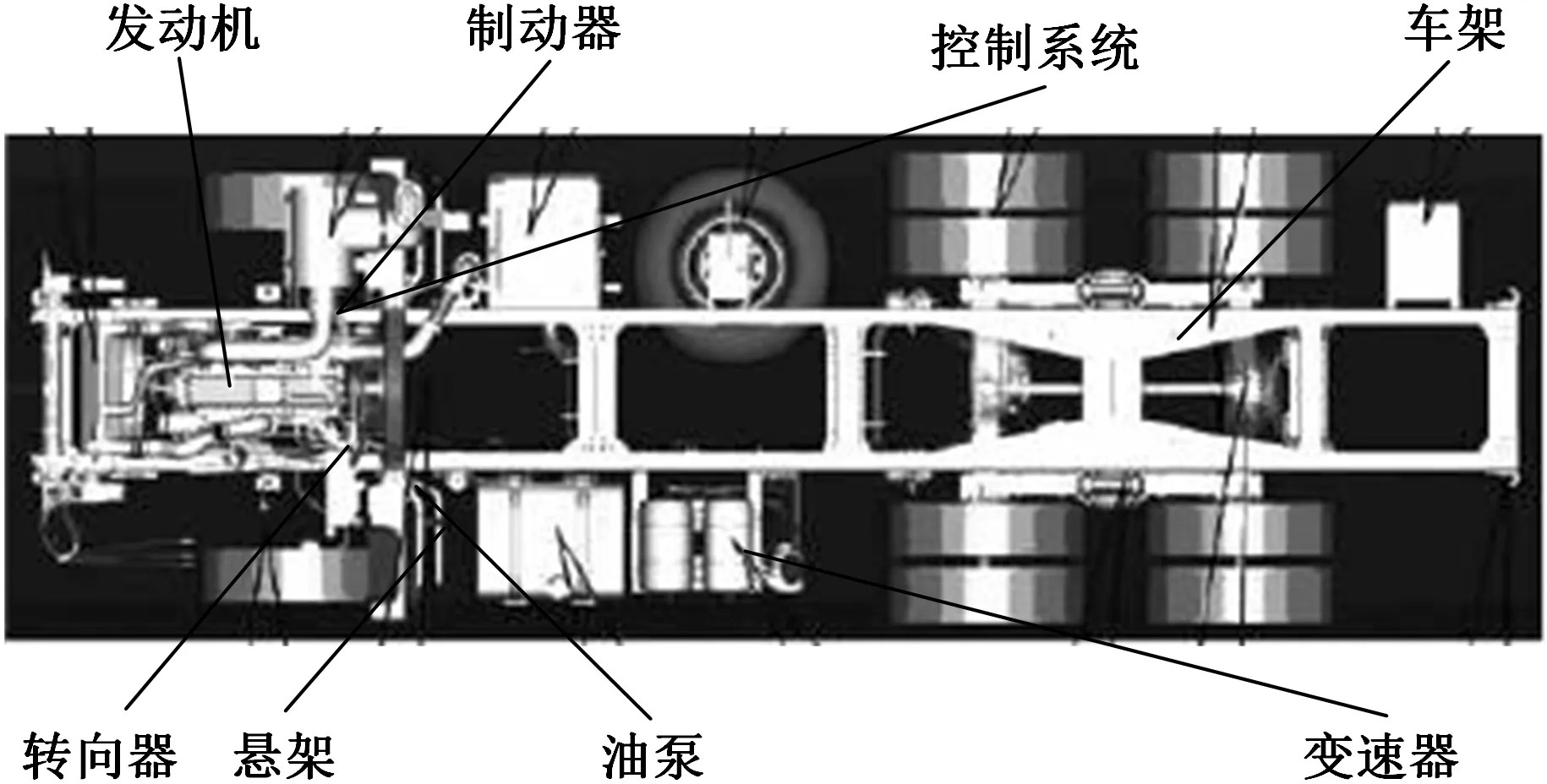
圖6 客車底盤模塊結構圖Fig.6 Bus chassis module structure

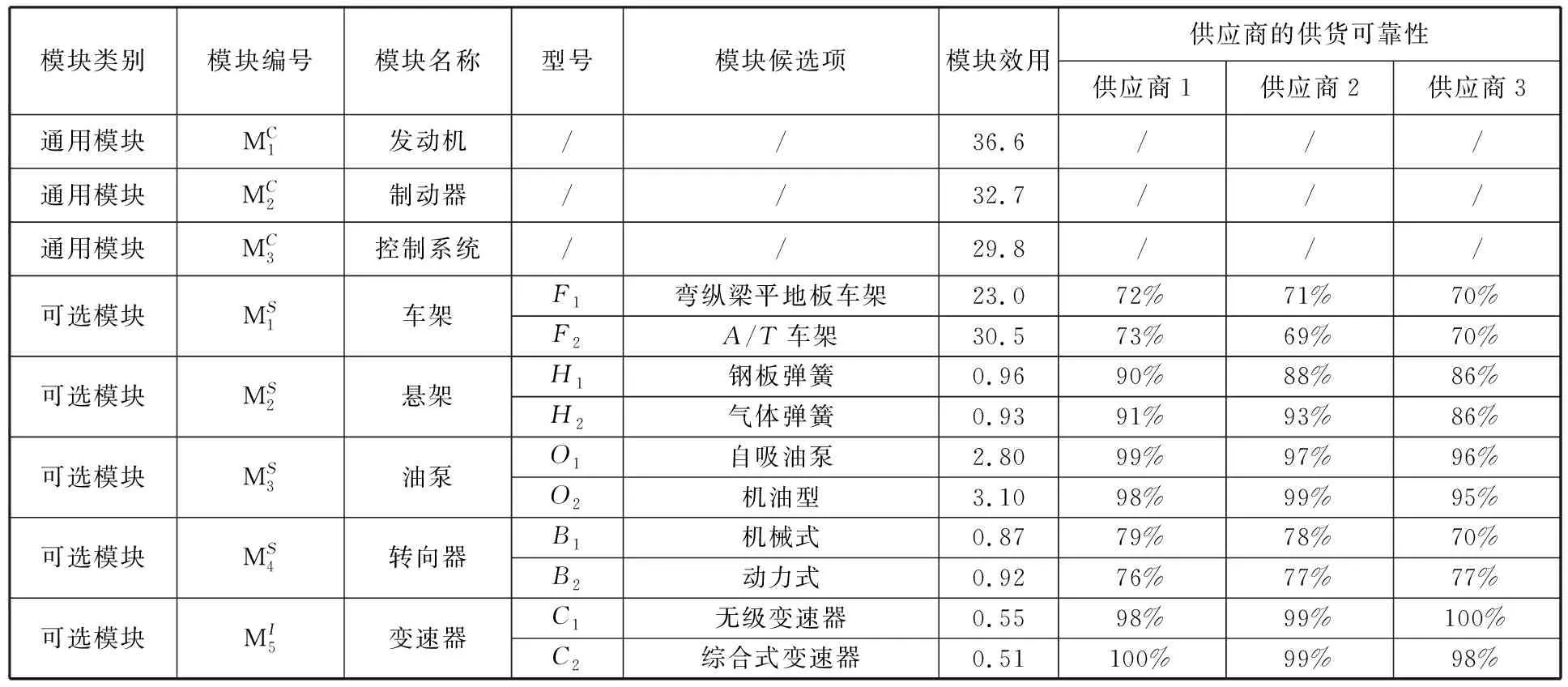
表1 客車模塊分類及效用

注： “/”表示不考慮型號，沒有模塊候選項和供應商

根據企業調研和實際生產情況，本案例中客車底盤產品族的供應商采購成本和組裝成本等已知信息見表2。總成本為不同模塊在選擇不同供應商時，供應商采購成本和風險成本的綜合。

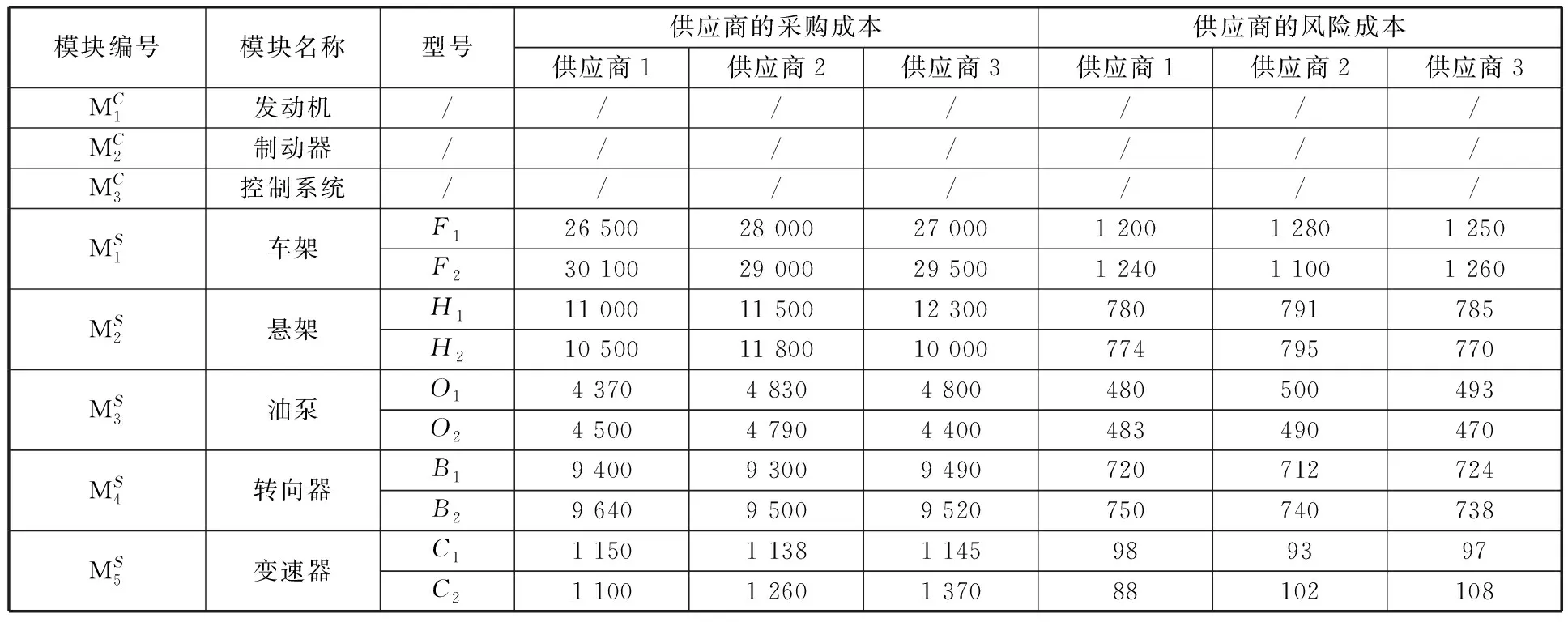
表2 供應商采購成本和組裝成本

3.2 計算求解

由于本文研究的模型為雙層規劃模型，解析方法很難準確求解，而智能遺傳算法較為適用于非線性規劃且含有0-1變量的問題，因此本文采用遺傳算法對含有0-1變量的雙層規劃模型進行求解，利用MATLAB工具箱中的遺傳算法功能實現。為了進一步優化，本文分別對產品數J取值為2、3，復合模塊數R取值為2、3，即求解4次，比較得到最優值。設定初始種群規模為100，交叉概率為0.8，變異概率為0.01，迭代次數為200。計算結果趨勢圖見圖7。由于縱坐標是產品類別和復合模塊不同情況下的函數值，且把4組迭代次數為200的函數值放在同一個圖表中，故縱坐標跨度較大，這導致函數收斂結果從直觀來看收斂速度較快，其實則不然，每種情況都需要經過較多次迭代才趨于穩定，所得解滿足雙層規劃約束域且算法全局收斂。

圖7 趨勢收斂圖Fig.7 Trend convergence graph

傳統結合供應商設計的產品族配置過程中使用的優化方法主要有兩階段單層優化(non-joint optimization,NJOP)和集成單層優化(all-in-one，AIO)方法。兩階段單層優化中第一階段以效用最大為目標，進行產品族架構設計優化；第二階段以成本最小為目標，進行供應商選擇設計。這種方法把一個問題割裂為兩個問題來進行優化，與雙層優化相比，不具有完整性。集成單層優化通過建立單目標優化模型來同時進行產品族架構與供應商設計，其目標是最大化的效用與成本。集成優化方法把兩個主體的優化問題合二為一，不能準確表示模型。

3.3 結果分析

由圖7及表3可以看出，在J=3，R=3的情況下，取得最優值。當J=3，R=3時，上下層目標相互關聯優化。表3給出了最優情況下的具體結果，在J=3，R=3的情況下，產品族架構設計最優的效用與成本的比值為0.000 598 66，總成本為554 000 000元。最優方案的產品族架構設計方案和供應商選擇方案具體分析如表4和表5所示。

3.4 靈敏度分析

采用遺傳算法研究參數μ對上層和下層目標函數最優值的影響，即敏感度分析。μ的取值從0.1到2.1，每次增加0.2，觀察上下層目標函數的變化范圍，見圖8。從圖8中可以觀察到，μ的取值范圍為0.1～1.3時，下層優化的目標函數值不變，為554 000 000元；在1.3到2.1之間，隨著μ的變化，下層目標函數值不斷波動。μ取值在0.1到1.7之間時，上層目標函數值基本保持不變；μ取值在1.7到2.1之間時，上層目標函數值隨著μ的不斷增大而增大。

表3 最終方案

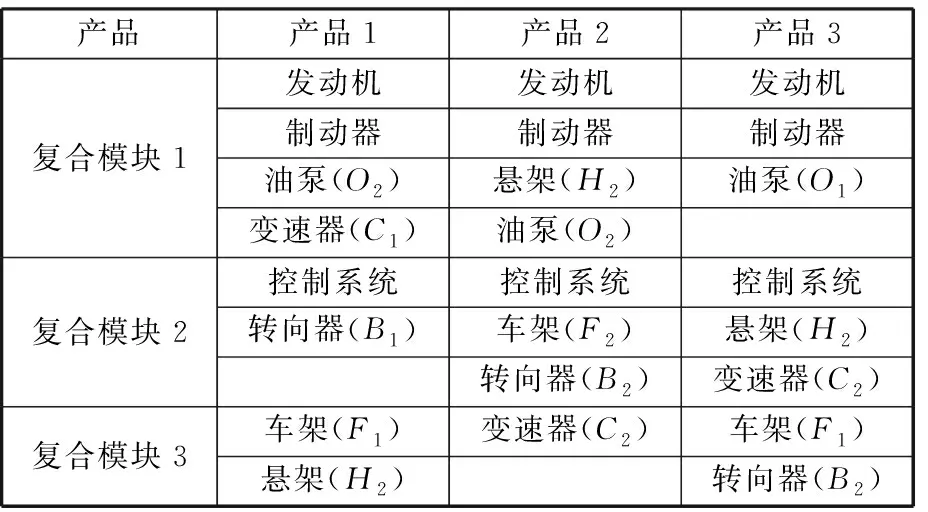
表4 產品族模塊選擇方案

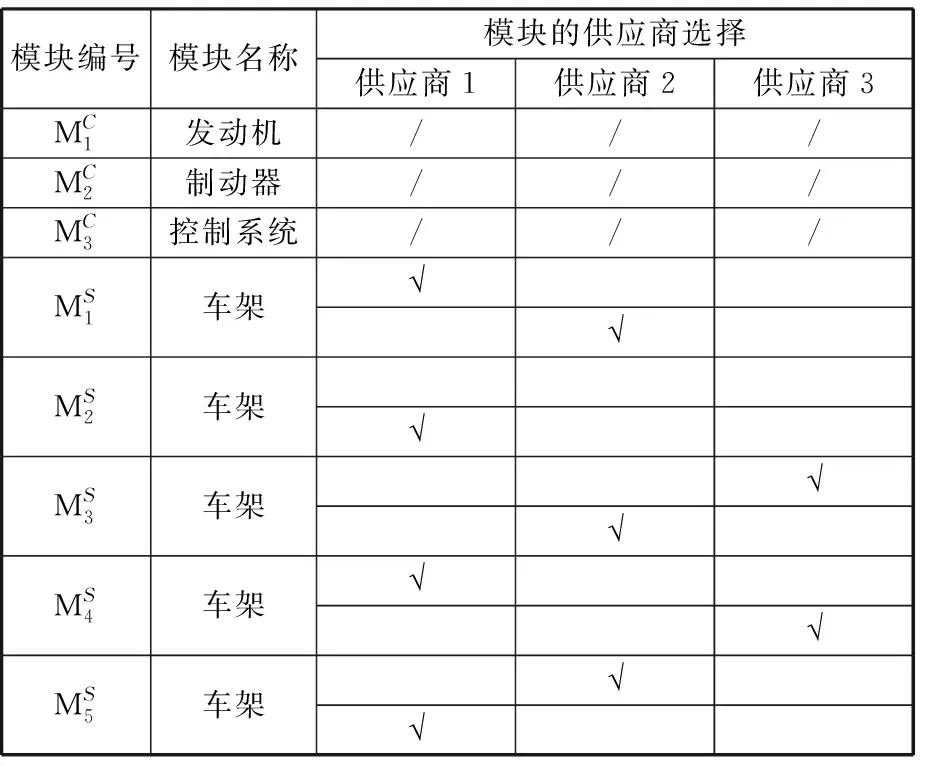
表5 供應商選擇方案

注：“”表示該模塊由相對應的供應商進行提供

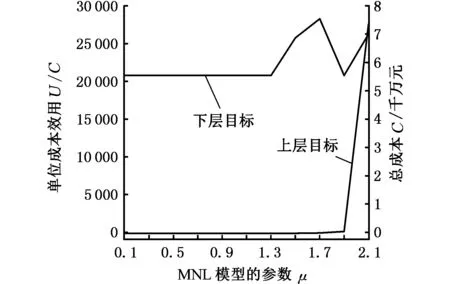
圖8 μ變化影響圖Fig.8 μ change impacts graph

由實驗可知，μ不僅可以影響上層目標函值，在一定情況下，也同樣影響下層目標函數值，因此，在客戶購買行為建模初期，公司應該對μ的正確校準給予足夠的重視。

4 結論

本文對產品族架構設計與供應商選擇問題進行研究，建立了產品族架構設計與供應商選擇問題協同優化的主從關聯優化模型，并應用于客車底盤產品族案例。通過分析計算認為,產品族架構設計與供應商選擇問題是相互關聯且具有主從關系的，基于主從關聯結構建立模型，不僅可從工程視角展現產品族架構設計，也體現了供應商選擇問題對產品族架構設計的反饋與要求。本文采用雙層嵌套遺傳算法及相關處理策略更符合關聯優化模型的特點，所得解滿足雙層規劃約束域且算法全局收斂。本文將產品族架構設計與供應商的設計進行關聯優化，不僅能夠使產品的總成本達到最小，也保障了客戶的效用最大化。本研究能夠幫助企業的決策者更好地對產品進行設計，為企業增加利潤的同時，有效提高企業的競爭力。另外，本文所給出的客車底盤產品族的應用案例表明主從關聯優化方法可得到更加合理的結果。