基于改進應變能密度法的電動輪自卸車車架焊縫疲勞壽命預測

米承繼 谷正氣 蹇海根 張 勇 李文泰 余 冰

1.湖南工業大學機械工程學院，株洲，412007 2.長沙理工大學工程車輛輕量化與可靠性技術湖南省高校重點實驗室，長沙，410114 3.湖南大學汽車車身先進設計制造國家重點實驗室，長沙，410082

0 引言

電動輪自卸車是1 000萬噸以上大型露天礦山場所運輸的主力軍，常年在礦山坑洼路面行駛，環境惡劣，工況復雜。車架作為最主要承載部件，其疲勞可靠性能是保證車輛正常作業和安全運行的關鍵因素。電動輪自卸車車架大多由高強度低合金調質中厚鋼板拼焊而成，實際運行過程中往往在結構薄弱焊趾處發生開裂。由于車架結構幾何形狀復雜多變、截面尺寸大小和形式多樣、載荷呈隨機性且單個鉸接位置受力達數十噸，損傷機理極其復雜，顯然難以通過傳統焊縫疲勞模型進行壽命理論計算或者利用疲勞試驗來研究車架焊縫失效機理。因此，結合焊接接頭微宏觀性能試驗和高精度理論模型進行數值模擬來研究電動輪自卸車車架焊縫疲勞可靠性問題很有必要。

焊縫失效的一種常見類型是焊趾處受垂直焊縫方向拉應力[1]，使焊趾處的缺陷發展，并最終導致結構失效。因而，求解焊縫的結構應力是進行損傷機理分析和疲勞壽命預測的關鍵因素。文獻[2-4]利用線性外推法將結構應力表征為母材橫截面內的拉應力和剪切應力，結合有限元法計算焊縫結構名義應力或熱點應力。然而，對于復雜載荷作用下的焊縫結構應力數值計算大多強調結構在線彈性階段的力學行為，這會忽略焊縫因為塑性變形而造成的疲勞損傷。文獻[5]結合彈塑性力學理論和工程技術拓展臨界平面法，提出利用非線性方程來描述臨界平面內拉應力和剪切應力與拉應力疲勞極限和剪切應力疲勞極限，該方法能夠預測焊縫的多軸比例和非比例循環加載疲勞壽命，但是對于復雜結構的工程實際問題至今仍然沒有可靠的方法來高效確定臨界平面的位置。為避開這一困擾，文獻[6-8]通過焊縫結構的彈塑性力學模型求解應力應變響應，結合最大局部應力應變和應力應變疲勞壽命方程來評價剩余壽命，同時為保證數值求解計算精度，文獻[9]還考慮焊縫的殘余應力及熱處理對焊接接頭疲勞強度的影響，文獻[10]提出利用三維激光掃描技術來構建焊縫精細化數值模型。然而，模型精度的提高并未從根本上解決焊縫壽命高精度預測問題。進而，文獻[11-14]提出將彈塑性應變能量密度作為衡量焊縫疲勞損傷的參量，從能量轉化角度揭示疲勞失效過程中焊縫損傷演化機理。

能量法與其他局部應力應變方法最大的區別在于，能量為一標量，能夠有效避免矢量損傷參量所涉及的位置與方向問題。基于此，本文首先針對文獻[12]構建的應變能量密度疲勞損傷模型進行改進，以拓展該模型對復雜載荷作用下材料或結構應力應變響應出現非完全封閉而交叉現象的表征能力。其次，開展高強鋼焊接接頭機械性能和疲勞試驗研究，獲取焊縫疲勞性能參數。再次，在電動輪自卸車車架有限元模型得到試驗驗證的基礎上，開展多載荷步非線性有限元分析，根據數值計算得到的應力應變響應進行應變能量法疲勞壽命預測，并將預測結果和實際開裂位置進行對比分析。

1 應變能量密度法的改進

單一載荷循環作用下的結構應力應變響應一般為一完全封閉的曲線，其相應的彈性應變能密度和塑性應變能密度計算方法見圖1。

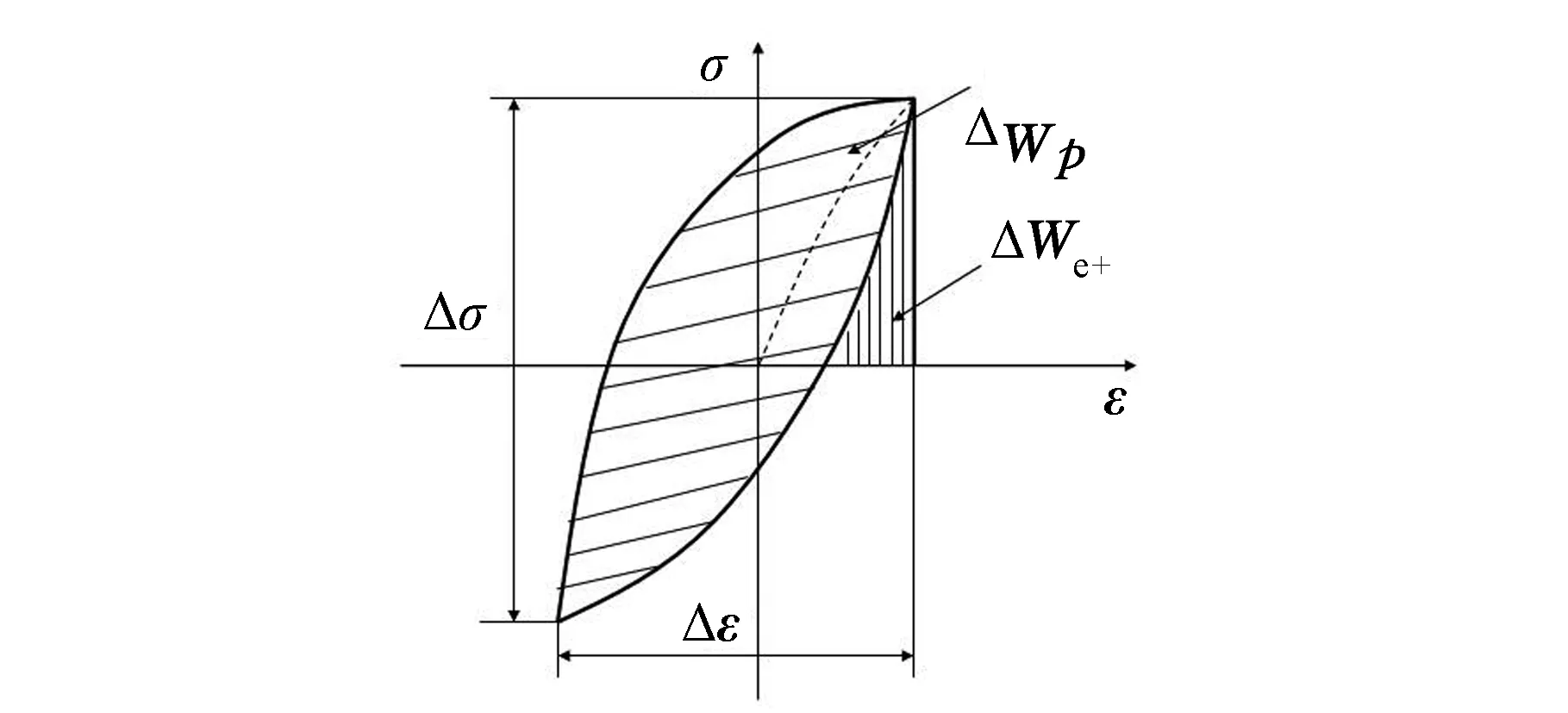
圖1 單一載荷循環作用下應變能密度計算Fig.1 Strain energy density calculation under single loading

根據圖1所示，當應力應變響應所圍成的是一完全封閉的滯回曲線時，其拉伸正彈性應變能密度ΔWe+可表示為

(1)

為體現平均應力的影響，式(1)還可改寫為

(2)

式中，σmax為拉伸最大應力值；E為彈性模量；Δσ為循環應力范圍；σm為平均應力。

當材料承受壓縮應力時，不會對疲勞損傷起作用，因而，不需要計算拉伸負彈性應變能密度。

單一載荷循環作用下的塑性應變能密度ΔWp可表示為

(3)

根據材料的循環應力應變本構方程，塑性應變能密度ΔWp可改寫為

(4)

式中，Δεp為塑性應變范圍；n′為應變硬化指數。

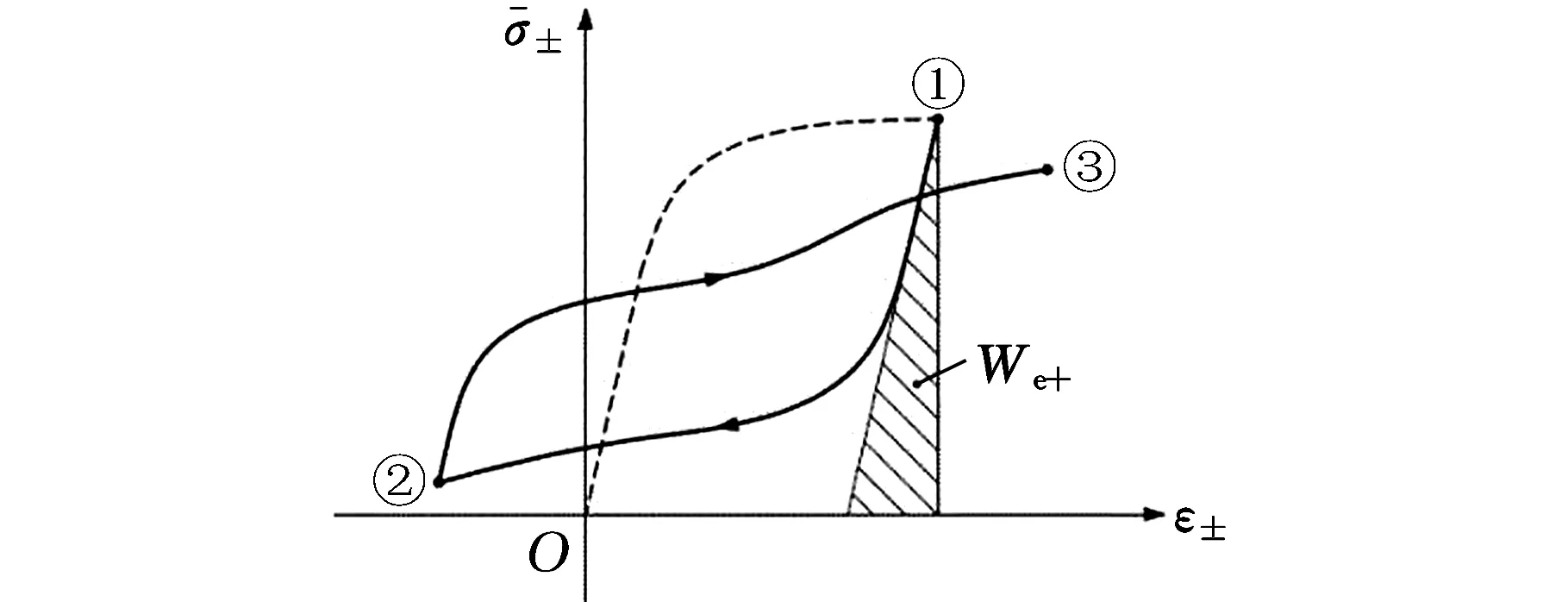
然而，對于實際焊接結構，往往會承受復雜的載荷作用，且在其循環加載作用下，焊縫會產生循環軟化或硬化效應，使得應力應變響應發生相應的變化，以至于在載荷循環作用下出現應力應變曲線相交叉，呈現為一非完全封閉的曲線。為此，本文在已有的應變能密度求解方法上進行改進，將封閉環以外的部分塑性應變能密度也考慮進來，具體求解方法見圖2。

根據圖2所示，當應力應變響應所圍成的是一非完全封閉的滯回曲線時，其拉伸正彈性應變能密度ΔWe+可表示為

(5)

(a)彈性應變能密度計算方法

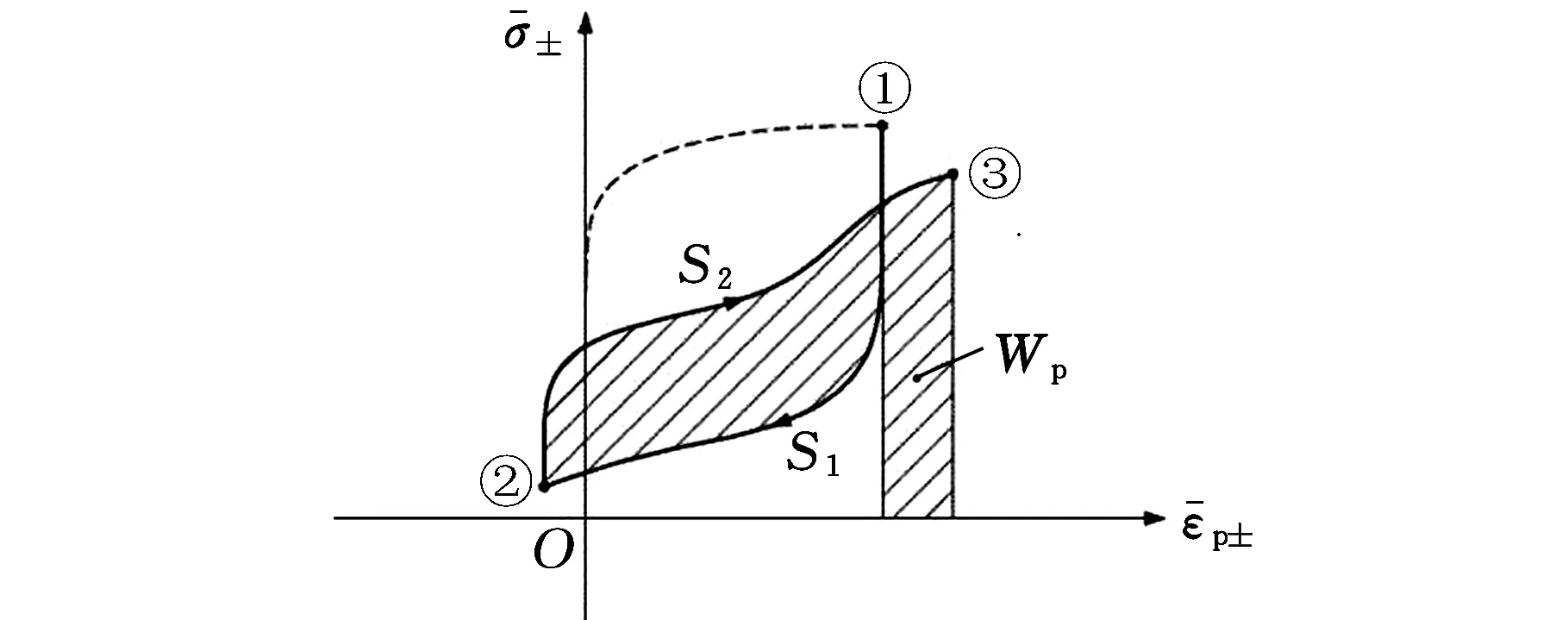
(b)塑性應變能密度計算方法圖2 復雜載荷循環作用下應變能密度計算Fig.2 Strain energy density calculation undercomplex loading cycle

對于同樣為非閉合的應力應變滯回曲線，塑性應變能密度可以由卸載和再加載所對應的面積組合而成，其具體的關系式可表示為

(6)

圖2中陰影部分的面積即為塑性應變能密度。與單一載荷作用下的塑性應變能密度求解相比，復雜載荷循環作用下的塑性應變能密度還包含封閉環以外的部分塑性應變能密度值，主要體現在式(6)等號右邊第二項。

總應變能密度作為衡量損傷的參數，可由塑性應變能密度和拉伸正彈性應變能密度相加得到，即

ΔWt=ΔWp+ΔWe+

(7)

2 焊縫材料參數獲取

本文主要研究電動輪自卸車車架對接接頭疲勞性能，因而設計一種厚度為6 mm的焊接接頭，試件的設計尺寸圖和實物見圖3。

2.1 機械性能參數

焊接接頭的單調拉伸試驗設備采用MTS 810型電液伺服萬能材料試驗機。基于位移控制，對試件施加軸向單調拉伸載荷直至試件被拉斷為止，焊接接頭安裝示意圖見圖4。由于該材料為高應變鋼材，為保護引伸計不因突發狀況而遭到破壞，在材料載荷發生明顯下降幅度時終止試驗。最后通過數據處理得到的焊接接頭工程應力應變曲線和真實應力應變曲線見圖5。

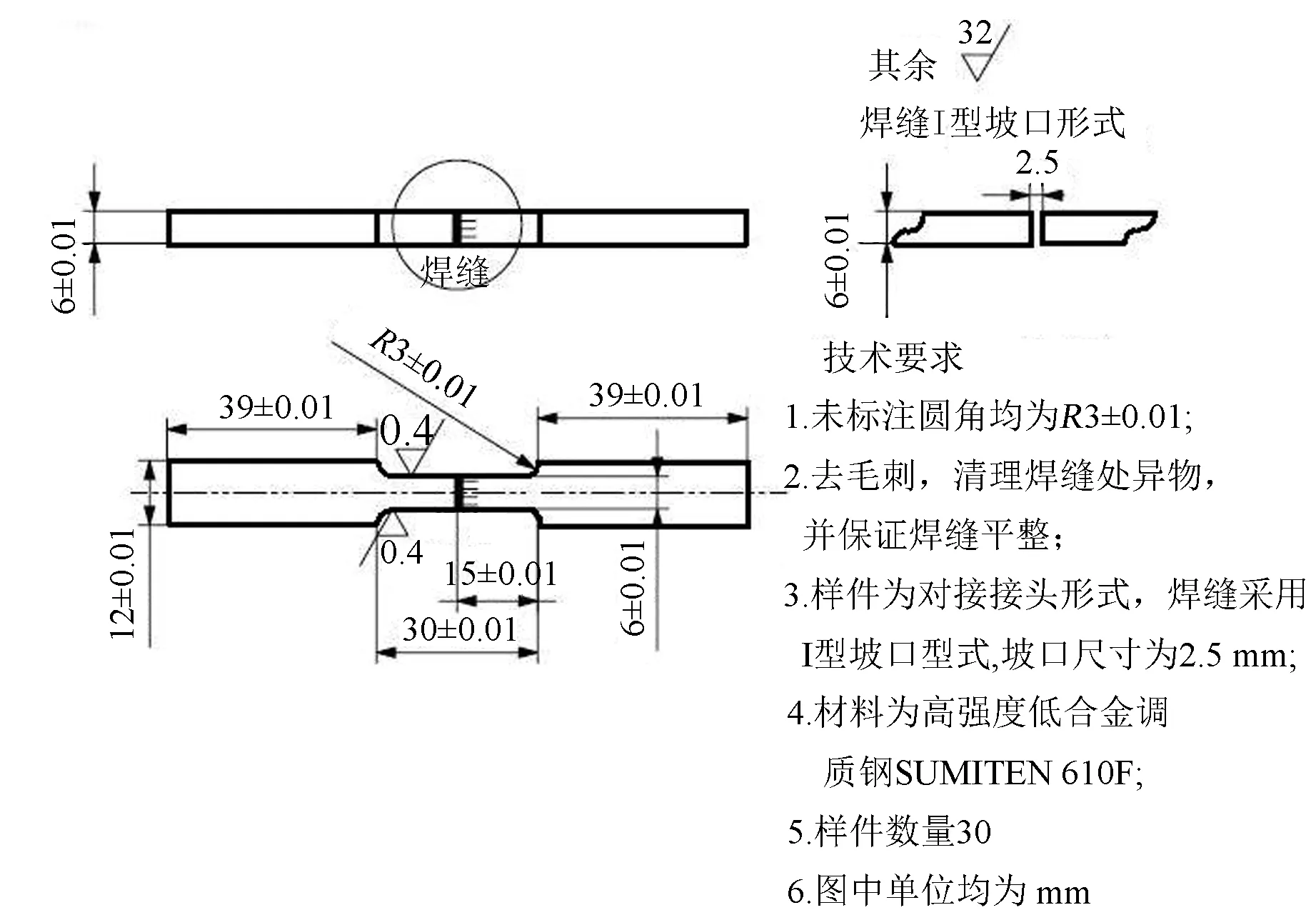
(a)焊接接頭試件尺寸

(b)焊接接頭試件實物圖3 焊接接頭試件Fig.3 Test specimen of welded joints

圖4 焊接接頭安裝示意圖Fig.4 Experimental schematic diagram of welded joints

圖5 焊接接頭應力應變曲線Fig.5 Stress-strain curve of welded joints

焊接接頭主要力學性能參數見表1。從測試結果來看，焊接接頭的彈性模量參數略高于母材，這主要是焊縫區域在焊接過程材料硬化所致；其他性能參數與母材比較接近，這間接說明，該焊接接頭的機械力學性能良好。

2.2 疲勞性能參數

基于應變控制的焊接接頭試件疲勞壽命試驗，首先需要確定不同的應變水平，通常情況下，初始應變水平可以取為略高于屈服極限所對應的應變值， 其他應變水平可以根據材料屬性逐漸減小，本文研究的焊接接頭應變水平分布為0.45%、0.35%、0.25%、0.15%和0.1%。

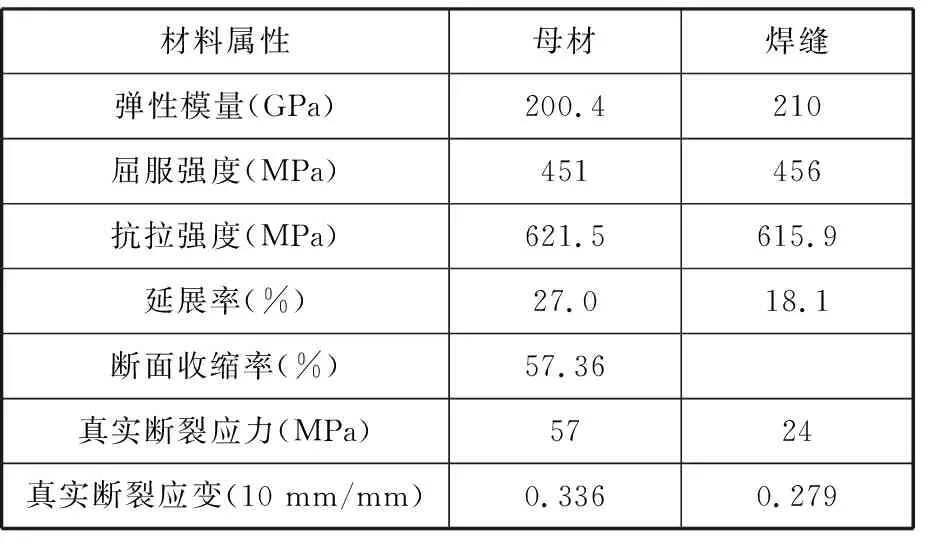
表1 焊接接頭機械性能參數

根據試驗結果，并結合疲勞壽命所對應的應力應變響應曲線，可以求出相應的應力幅值、應力范圍、彈性應變幅值、塑性應變幅值，從而得到對數彈性應變幅值、對數塑性應變幅值與對數疲勞壽命的關系曲線，見圖6，可以看出，擬合曲線和試驗結果比較接近。

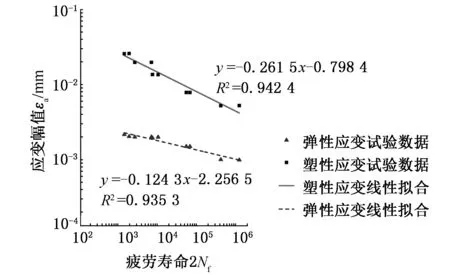
圖6 彈塑性應變疲勞壽命試驗結果Fig.6 Elastic and plastic strain and fatigue life test results

借助引伸計同樣可以得到不同應變水平下的周期應力應變數據，其中某一試件的周期應力應變曲線見圖7，可以看出，焊接接頭試件在應變不變的情況下應力峰值明顯減小，屬于材料循環軟化行為。另外， 其次周壽命的滯回曲線面積與半周壽命的滯回曲線面積相差不是太大，說明材料

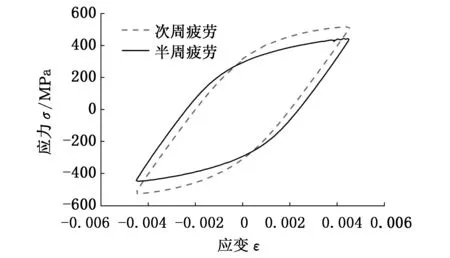
圖7 某試件周期應力應變響應曲線Fig.7 Cyclic stress-strain curve for one specimen

在一定載荷作用后很快達到穩定狀態。

(8)

式中，εa為應變幅值；Δσ/2為應力幅值；K′為循環強化系數。

結合車架焊縫應變疲勞壽命試驗和Ramberg-Osgood方程，得到的周期應力應變響應見圖8。由圖8可看出，擬合的曲線與試驗數據吻合良好，能夠有效模擬車架焊縫的周期應力應變行為。式(8)的參數值在表2給出。

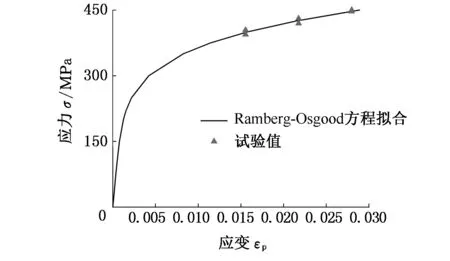
圖8 周期應力應變響應Fig.8 Cyclic stress-strain response

表2 車架焊縫疲勞材料參數

要實現車架焊縫基于應變能量法的疲勞壽命預測，還需要得到材料的應變能密度和疲勞壽命的關系。結合應變能密度計算方法和周期應力應變響應曲線，即可求得不同應變水平下的總應變能密度，然后找到對應的疲勞壽命值，通過數學方程擬合得到焊縫疲勞材料特性。參考文獻[11]，本文利用冪函數擬合總應變能密度和疲勞壽命的關系，其一般數學方程可表示為

(9)

式中，Nf為疲勞壽命；A為應變能密度系數；B為應變能密度指數。

結合車架應變疲勞壽命試驗數據，式(9)的參數值見表2。其中，車架焊縫應變能密度疲勞壽命曲線見圖9。由圖9可看出，擬合曲線與試驗結果相差不大，冪函數能夠有效表示兩者的關系。

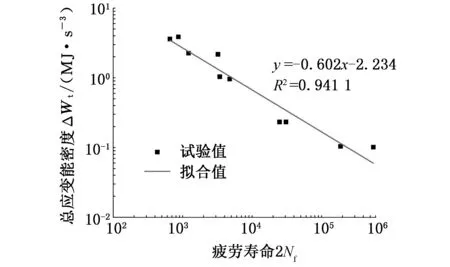
圖9 總應變能密度疲勞壽命曲線Fig.9 Total strain energy density and fatigue life curve

3 車架多載荷步非線性有限元分析

3.1 有限元模型建立及驗證

考慮到車架是由各種厚度的鋼板和一部分圓管組合焊接而成，具有薄板結構特性,存在膜應力狀態,同時考慮模型的大型性和計算硬件的實際情況等，決定采用殼單元對車架進行離散。電動輪自卸車車架上負載質量較大的部件主要有動力總成、燃油箱、貨物與車廂、左、中、右甲板、散熱器以及液壓油箱，其重心位置均通過其幾何結構的質心求得，主要的集中質量點利用Mass單元模擬，剛性耦合連接利用Rbe3單元模擬，得到的車架有限元模型的單元總數為87 932，節點總數為82 867。最終建立的車架有限元模型見圖10。

收縮裂縫主要是指混凝土因外界因素所致的體積變化，一般情況下是干縮裂縫與塑性裂縫，其中塑性收縮裂縫的發生時間主要在混凝土初凝階段，此時具有較高的水化反應，水分會出現大量增加的情況，導致混凝土失收縮。干裂裂縫主要在混凝土硬化前后，表層混凝土水分散發比較快，內部結構熱量散發相對較慢，直接導致混凝土表面收縮性相大，內部收縮性小，致使收縮情況產生一定的不均勻，從而發生收縮裂縫現象。

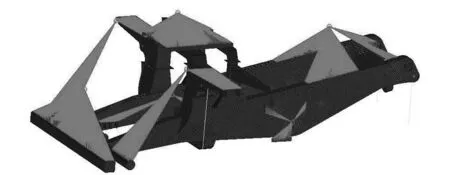
圖10 車架有限元模型Fig.10 Finite element model of frame

車架在滿載靜止狀態下主要承受各附加裝置以及貨物的重力，重力通過對建立的質量點單元施加重力加速度來實現；然后，對前后懸架下支點的自由度進行約束，釋放車架前進方向的自由度以及3個轉動自由度。通過MSC.Nastran數值求解計算，車架的最大主應力云圖和最小主應力云圖分別見圖11和圖12。可以看出，在車架縱梁底板與尾梁內側板拐角處的最大應力值達120 MPa，由于該位置結構幾何形狀較復雜，且受到貨物重力作用，因此應力水平較高。另外，車架縱梁頂板與尾梁內側板處、前后懸架鉸接位置和后牽引接頭位置，最大主應力水平分別在100 MPa、60 MPa和50 MPa左右，其他位置的應力水平均較低。

圖11 車架最大主應力云圖Fig.11 Maximum principal stress contour of frame

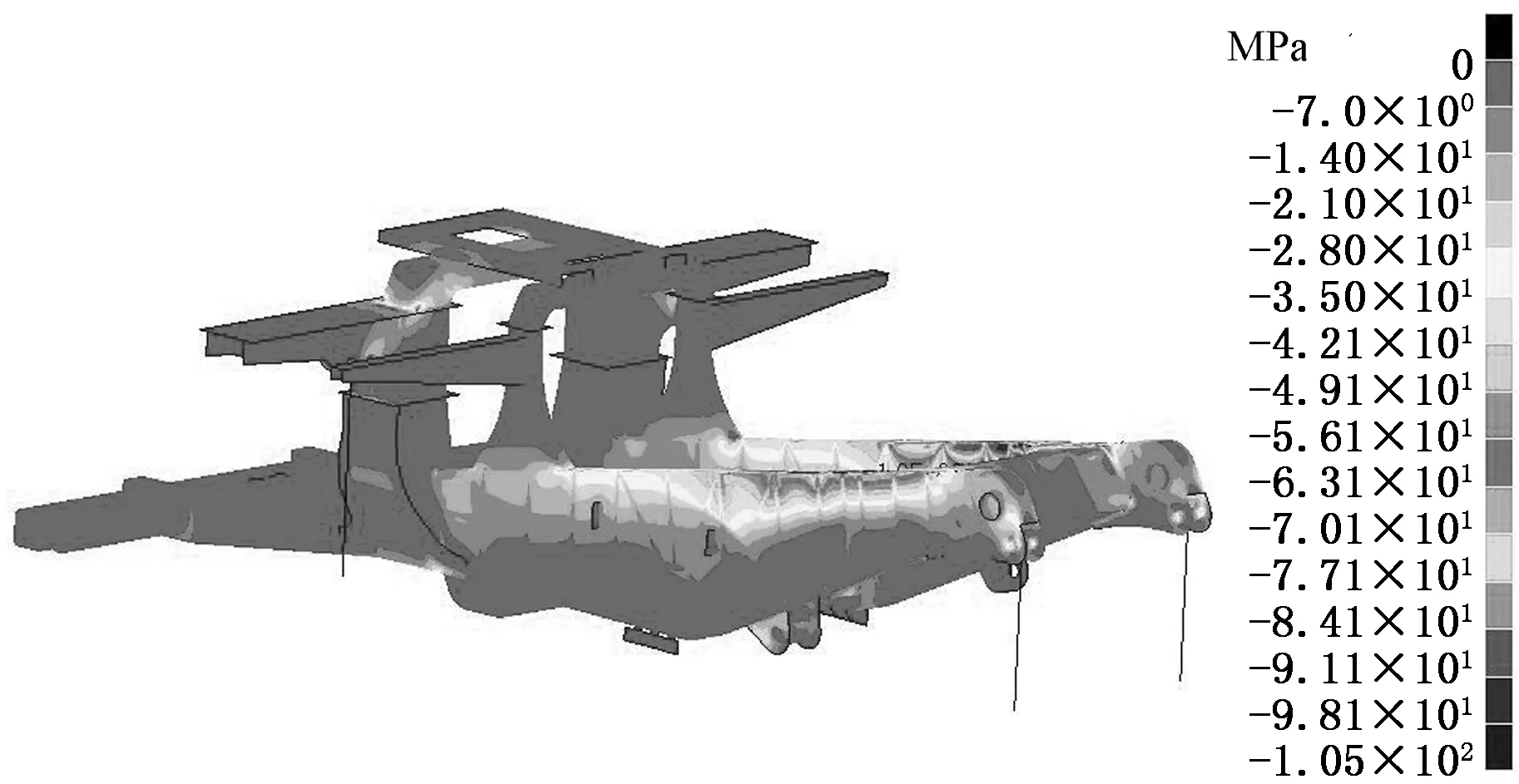
圖12 車架最小主應力云圖Fig.12 Minimum principal stress contour of frame

為驗證電動輪自卸車車架有限元模型的準確性，對車架滿載靜止工況下的應力狀態進行了測試。主要測試車架關鍵部位的應力值，從車尾往車頭方向標記，左邊定義為A，右邊定義為B，共包括11個測點，具體位置的測點見圖13，應變片具體安裝位置見圖14。

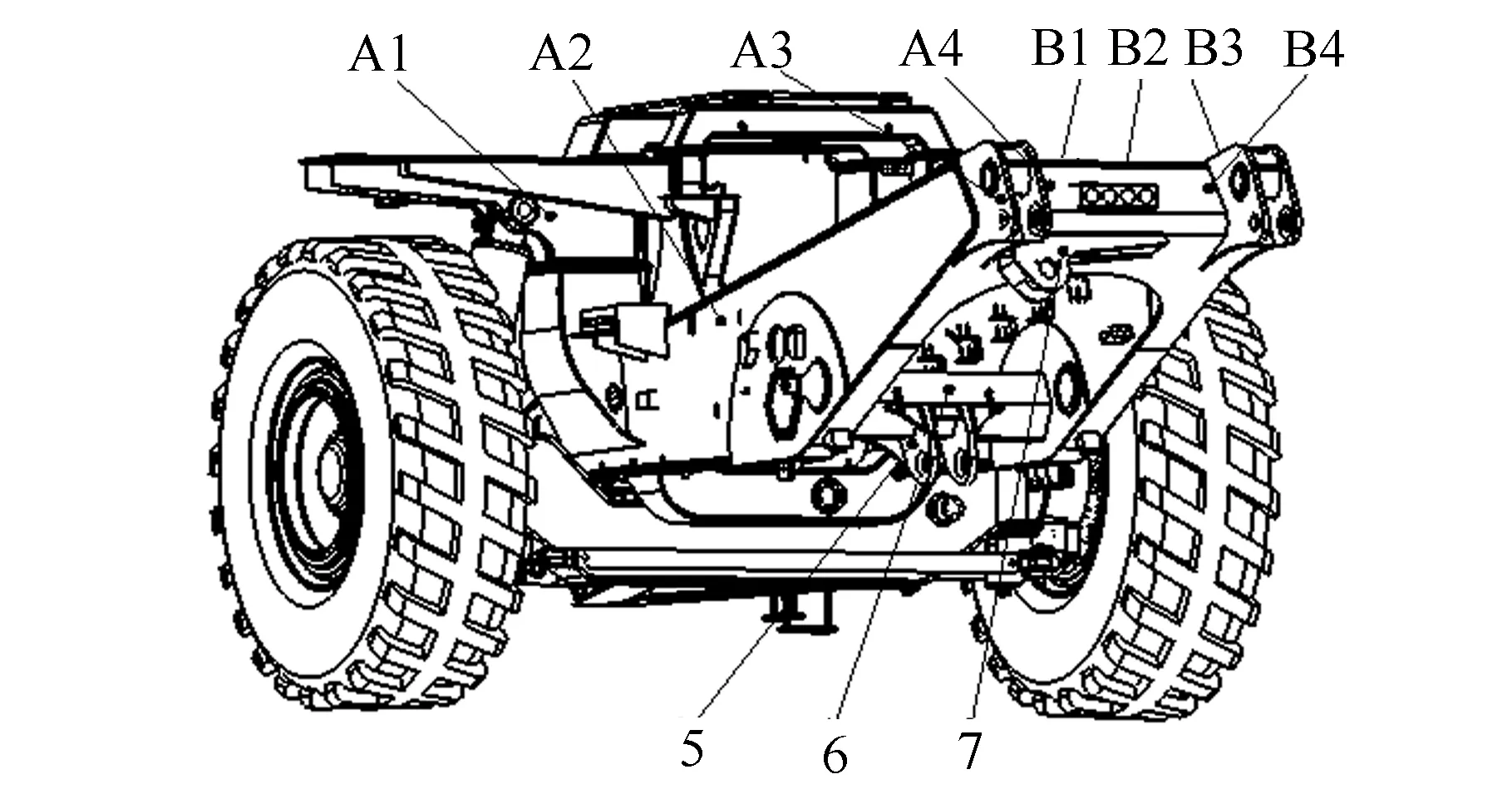
圖13 車架應力測點布置圖Fig.13 Measuring points layout of frame stress

圖14 測點B4應變花安裝示意圖Fig.14 Strain rosette schematic diagram of point B4

將車架有限元分析應力結果和主要測點試驗應力值進行對比，結果見表3。可以看出，測點7的誤差最大，達70.5%，主要是因為滿載靜態有限元分析僅考慮了垂直方向的載荷，在靜強度分析時沒有施加后橫拉桿鉸接位置處的局部側向作用力，后橫向穩定桿位置處主要傳遞側向載荷，實車結構可能由于貨物偏載造成局部受力不均而產生一定的應力，從而使得試驗結果和仿真結果誤差較大。測點A3和B3誤差達55%左右，其主要原因在于車架有限元模型忽略了車廂和車架之間的橡膠墊，將車廂和貨物重力直接施加于車架相應節點上，并且由于車架縱梁頂板和底板與車架尾梁之間存在幾何過渡，一定程度上造成該位置局部應力集中，從而出現大面積高應力區域，某種程度上造成了高應力區域的轉移。除上述測點誤差較大以外，其他測點的有限元分析結果和試驗結果誤差絕大部分在10%以內，部分有限元分析結果和試驗結果非常接近，從而充分驗證了本文所建立的車架有限元模型的準確性，也為后續依據該模型進行車架多載荷步非線性有限元分析奠定基礎。

表3 車架仿真和試驗應力結果對比

3.2 多載荷步非線性有限元分析

當車架焊縫的材料力學行為和結構載荷受力情況確定后，借助有限元分析對其進行求解計算，從而得到循環載荷作用下不同單元和節點的應力應變信息。根據試驗得到的應力應變響應數據，可以求出仿真分析所需要的塑性應變和應力之間的對應關系，并將其作為車架焊縫的非線性材料參數。然后將車架焊縫有限元分析分成3個載荷步，第一個載荷步為首次加載過程，模擬車架焊縫開始受到拉伸或壓縮作用；第二個載荷步為卸載過程，該過程是計算求出車架焊縫單元應力應變滯回曲線的必要步驟；第三個載荷步為再次加載過程。本文所需要的載荷來自多體動力分析[14]，分別對車架滿載水平路面和下坡轉彎制動路面的主要鉸接點載荷時間歷程進行等效處理。其中，滿載水平路面車架左前懸架和前橫向穩定桿主要受力方向等效載荷分別見圖15和圖16。

圖15 左前懸架y方向等效載荷Fig.15 Direction y equivalent loading at leftfront suspension

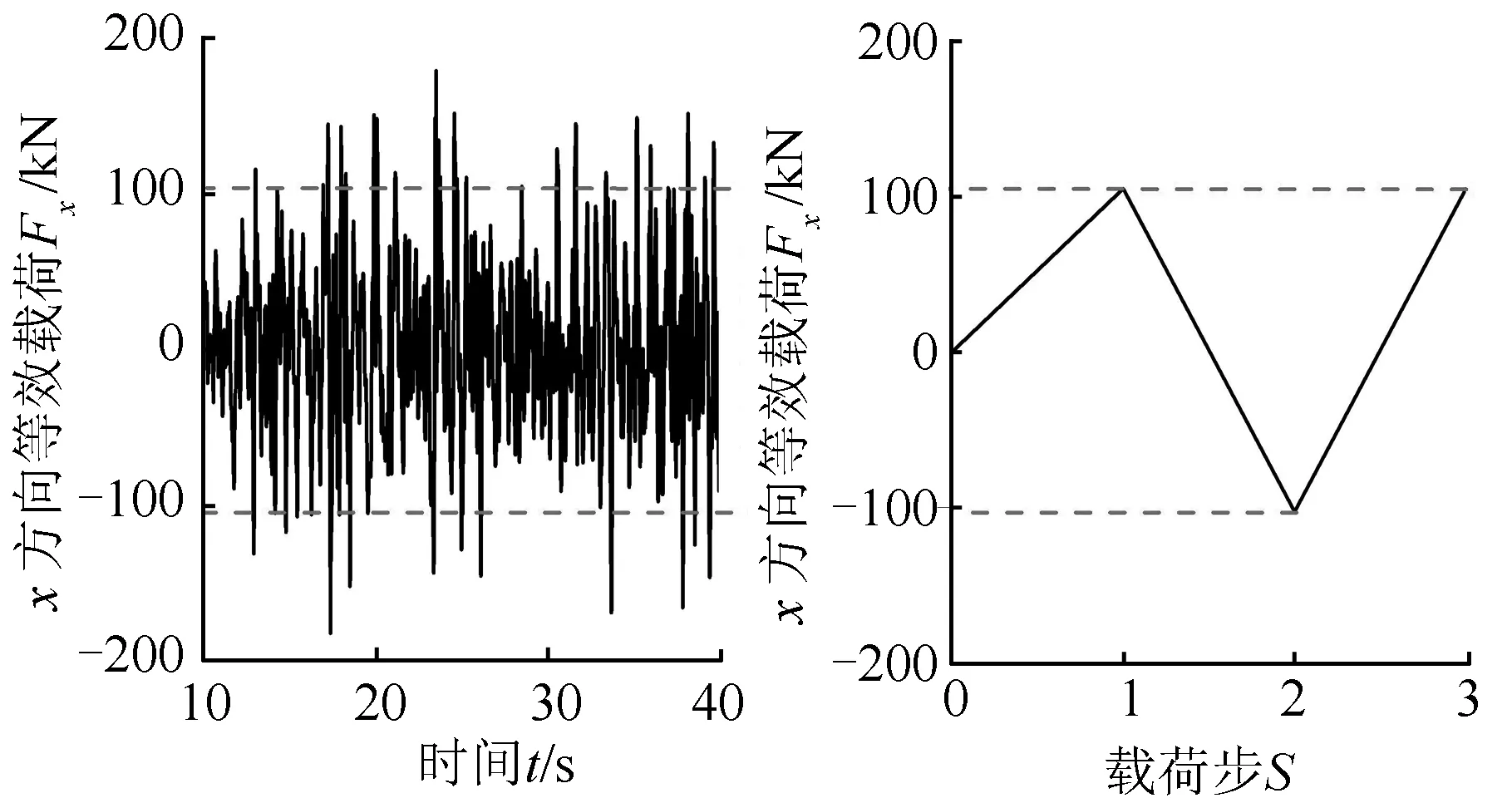
圖16 前橫向穩定桿x方向等效載荷Fig.16 Direction x equivalent loading at front stabilizer

車架焊縫在循環加載作用下進行的是有限元靜態分析計算，其載荷呈線性關系施加于有限元模型，考慮到油氣懸架非線性剛度特性對分析計算結果的影響，本文通過建立彈簧單元來模擬油氣懸架，并借助inp文件來定義其剛度與位移之間的非線性特性。通過計算得到的前后懸架非線性剛度曲線見圖17和圖18。

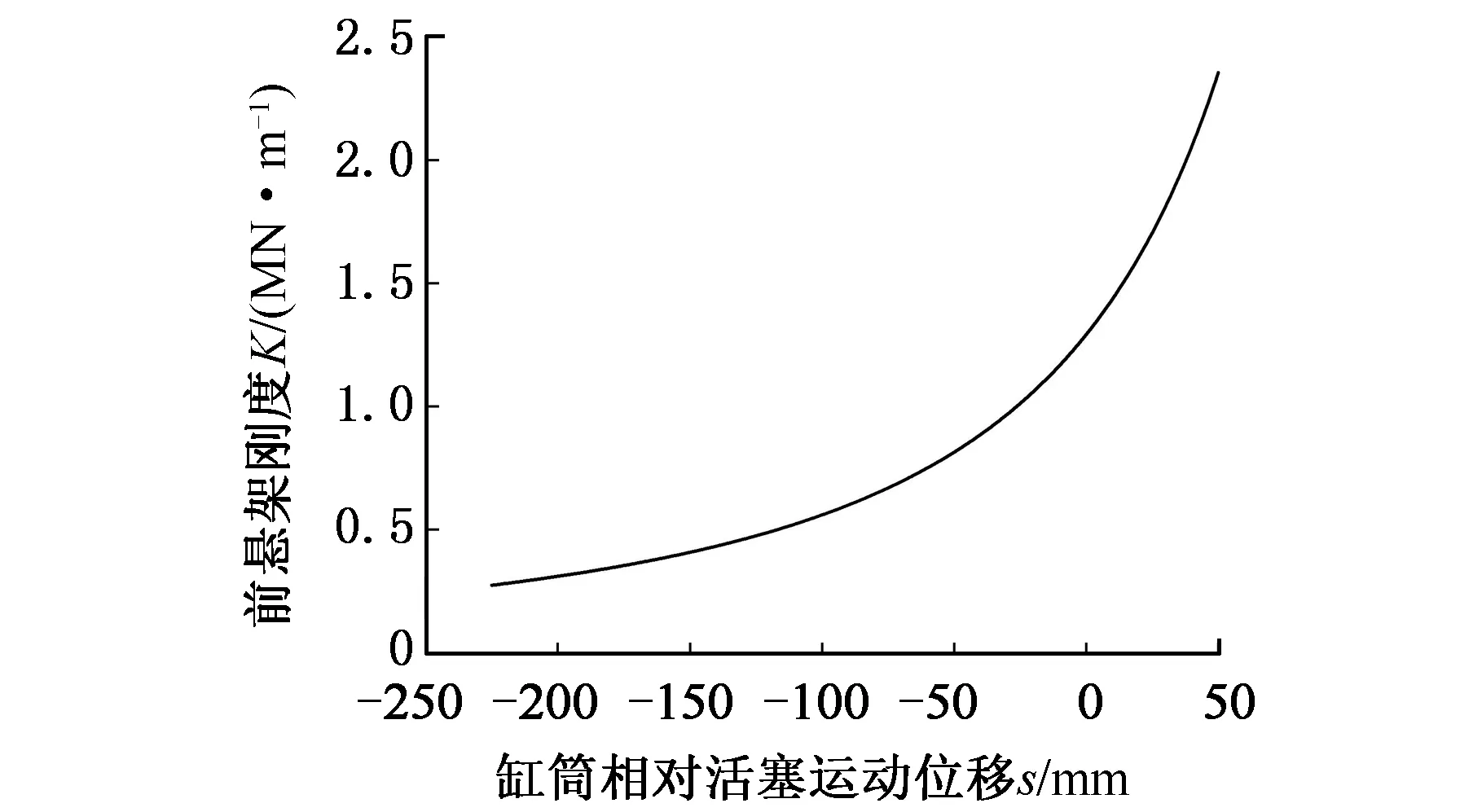
圖17 前懸架剛度曲線Fig.17 Stiffness curve of front suspension

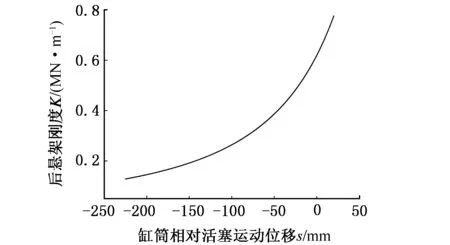
圖18 后懸架剛度曲線Fig.18 Stiffness curve of rear suspension

結合試驗得到的車架焊縫非線性材料行為，將其循環應力和相應的塑性應變作為材料參量，定義混合的各向同性與運動硬化法則，選擇半周數據類型；將建立的彈簧單元與車架主要鉸接點位置通過MPC-link方式耦合在一起，并約束彈簧下支點的自由度，將車架主要受力等效載荷施加于耦合節點上，就可以對車架焊縫有限元模型進行求解計算。本文分別對滿載水平路面行駛工況和下坡轉彎制動行駛工況進行多載荷步非線性有限元分析計算，第二次加載完成后利用ABAQUS求解計算得到的車架焊縫單元應力和塑性應變云圖見圖19～圖22。

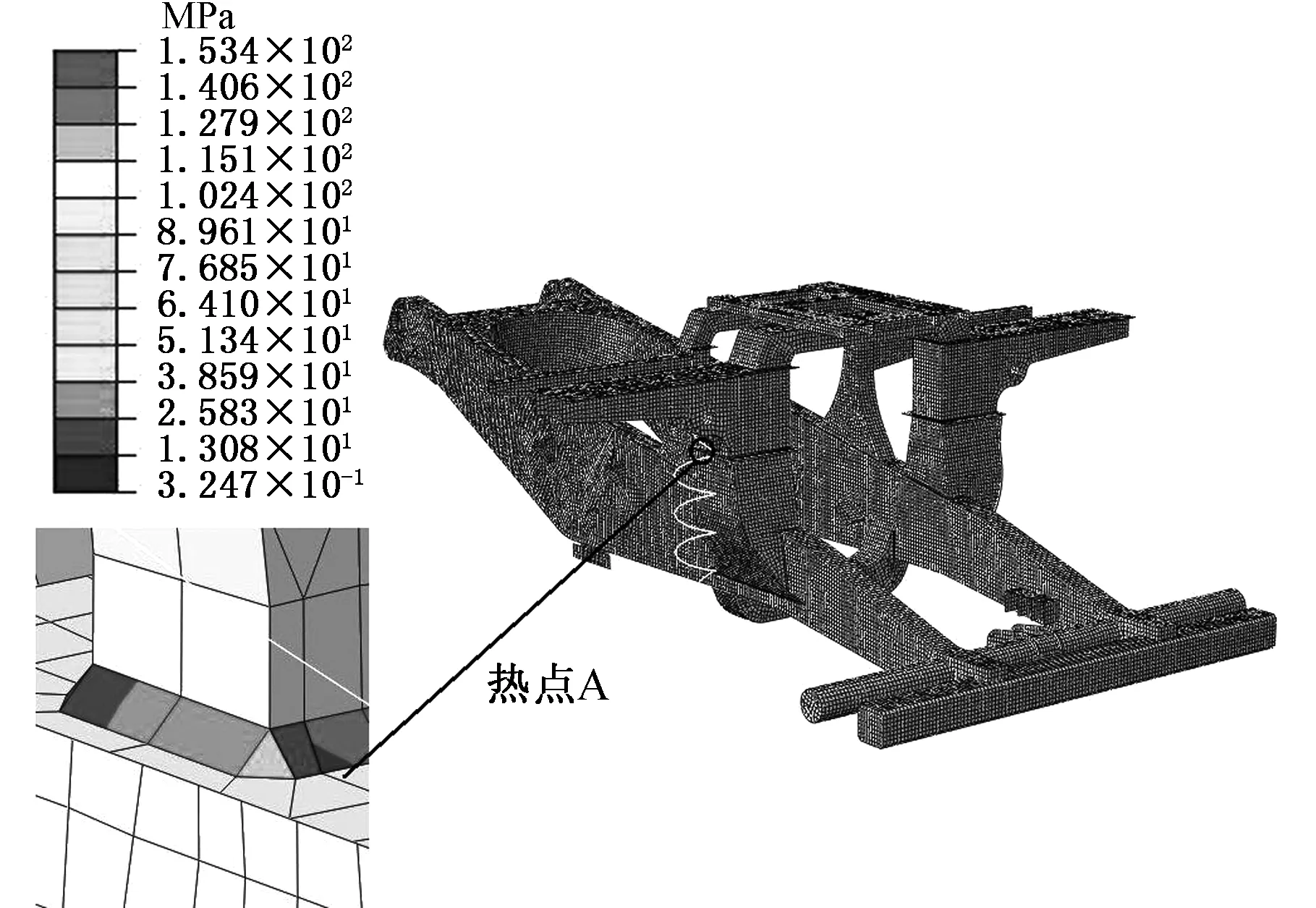
圖19 滿載水平路面車架焊縫應力云圖Fig.19 Stress contour of frame weld seams under full loading for horizontal road surface

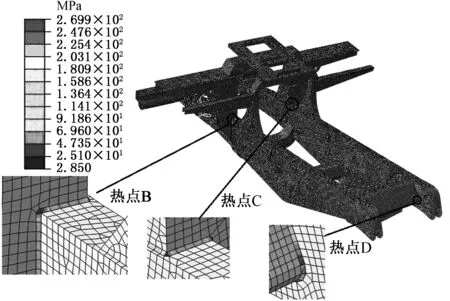
圖21 下坡轉彎制動路面車架焊縫應力云圖Fig.21 Stress contour of frame weld seams under full loading for downhill and turning road surface

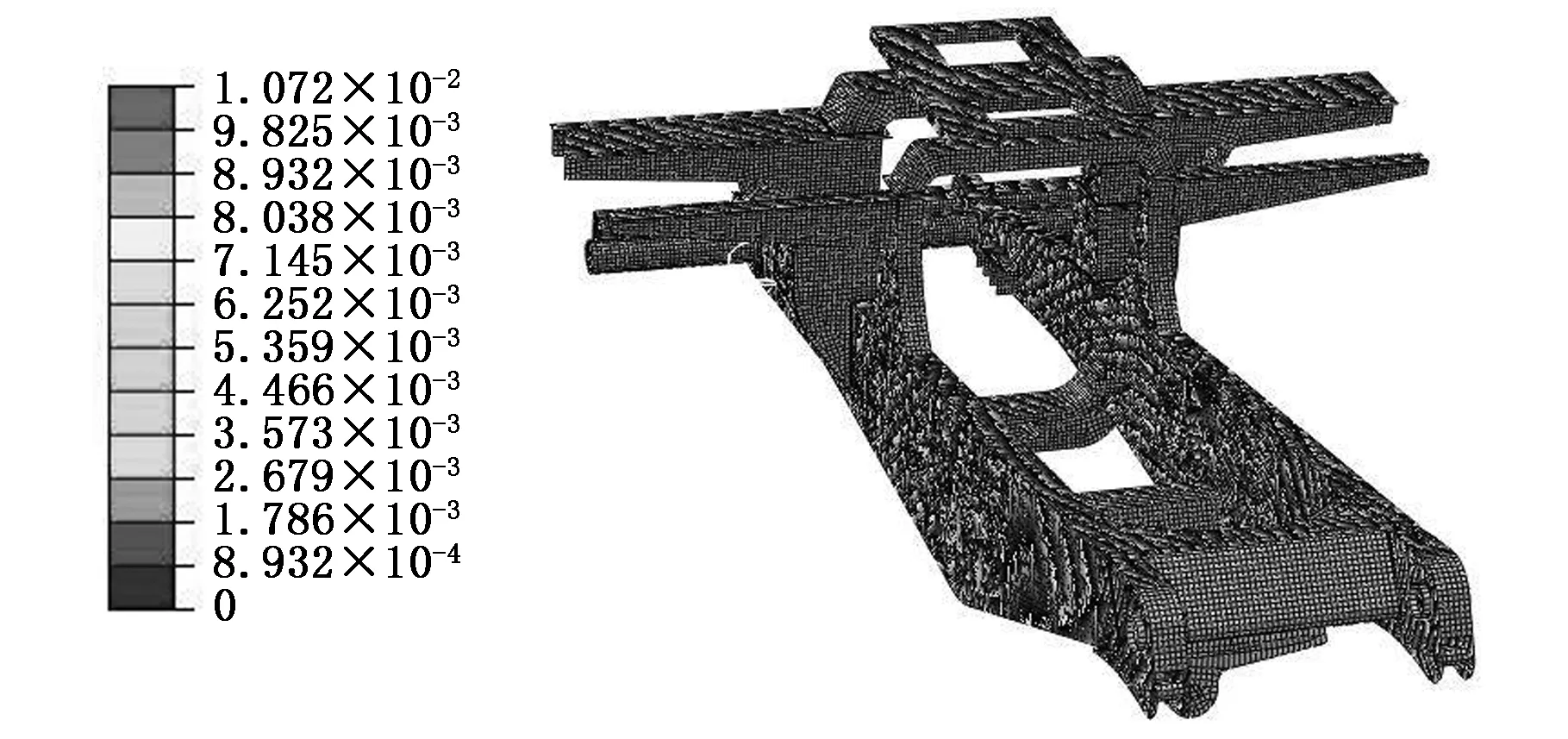
圖22 下坡轉彎制動路面車架焊縫等效塑性應變云圖Fig.22 Equivalent plastic strain contour of frame weld seams under full loading for downhill and turning road surface

由圖19可以看出，在滿載水平路面行駛工況下，最大等效應力為153 MPa，出現在車架右側龍門梁與右懸架筋板連接處，在該位置存在一定的幾何過渡，且焊縫結構形式較復雜，也是主要承載部位，因此出現較大的應力值。

由圖21可以看出，在下坡轉彎制動路面行駛工況下，最大等效應力為270 MPa(熱點D)，出現在車架右后懸架與尾梁筋板連接處，在該位置也存在一定的幾何過渡，且后懸架位置載荷較大，還受到后橫向穩定桿位置處的橫向載荷，屬于復雜交變載荷，因此出現較大的應力值。另外，在車架左右大梁位置與車架縱梁連接位置也出現了較大應力(熱點B和C)，應力值也達到260 MPa左右，因此這3處位置均為疲勞壽命分析計算關注的重要位置。

4 車架多載荷步非線性有限元分析

4.1 預測結果

對于滿載水平路面行駛工況，由靜態分析可知，其塑性應變非常小，主要成分為彈性應變能密度，只需要求出循環載荷作用下最大等效應力，再根據式(5) 即可求出相應的應變能密度。對于車架下坡轉彎制動路面行駛工況，存在一定的塑性變形，因此需要得到其循環載荷作用下的應力應變響應。不過，需要指出的是，車架主要承受垂直方向的載荷作用，因此，其應力應變量主要集中在主應力S11和主塑性應變P11上，如圖23a所示(熱點D)，而其他方向的應力應變值非常小，在此忽略不計；另外，車架焊縫單元除了承受拉壓載荷外，還承受其他方向的作用力，因此焊縫危險單元還具有剪切應力和剪切塑性應變，如圖23b所示(熱點D)。根據式(5)和式(6)，即可求出不同危險節點的彈性應變能密度和塑性應變能密度，從而結合應變能密度疲勞壽命曲線實現車架焊縫疲勞壽命預測，結果見表4。依據同樣的方法，可求得熱點B和C的彈性應變能密度和塑性應變能密度，從而根據總應變能密度確定其相應疲勞壽命值。由于熱點B和C與熱點D的應力應變曲線比較相似，本文不一一給出。

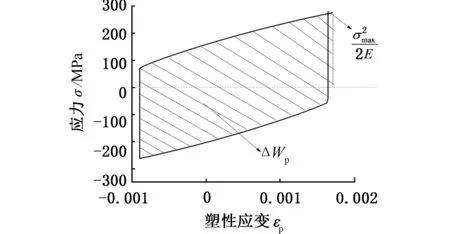
(a)主應力應變響應

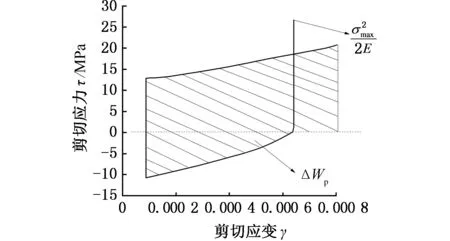
(b)剪切應力應變響應圖23 車架焊縫熱點D應力應變曲線Fig.23 Stress-strain curve of frame weld seam at point D

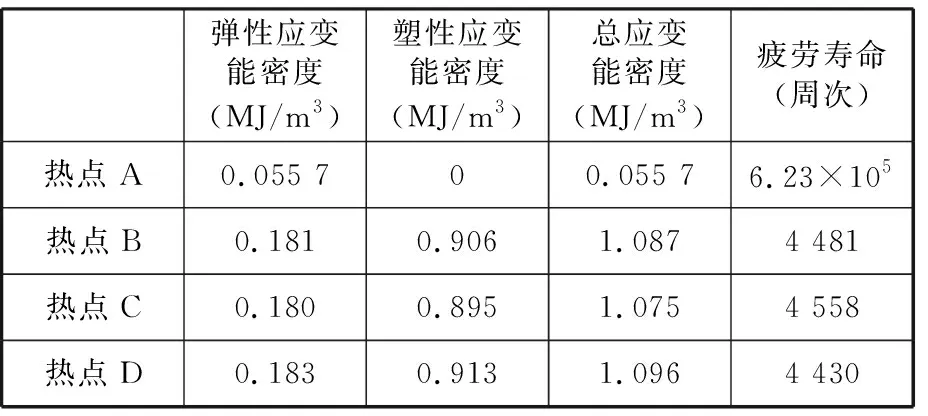
表4 應變能量法車架焊縫疲勞壽命預測結果

4.2 對比分析

為說明本文提出的改進應變能量法的有效性，將其疲勞壽命計算結果以及傳統應變能量法(不考慮封閉環以外的應變能密度)疲勞壽命計算結果與構件實際失效位置進行對比，見圖24和圖25，從裂紋的起始路徑和痕跡信息來看，屬于疲勞失效。而疲勞壽命預測的危險區域與實車焊縫開裂的位置非常接近，熱點B和熱點C對應于車架焊縫開裂位置1和2，這說明，基于應變能量法的車架焊縫疲勞壽命預測結果可靠。另外，在發現車架焊縫開裂位置1和2一個月之后，實車在預測的熱點D位置也發現了微小裂紋，由于礦山考查條件有限，未能給出開裂實物圖。在實際工作中，熱點D位置附近車架縱梁位置有橡膠墊緩沖裝置，而數值模擬計算中沒有考慮該因素，因此導致該位置疲勞壽命計算結果與實際失效時間存在誤差。

圖24 車架裂紋位置1(熱點B位置)Fig.24 Crack 1 in left frame beam (close to point B)

圖25 車架裂紋位置2(熱點C位置)Fig.25 Crack 2 in right frame beam (close to point C)

結合礦山實際工況考察，電動輪自卸車每天經過該下坡轉彎制動路面行駛工況的次數為10左右，同時考慮滿載水平路面工況造成的損傷(主要是彈性應變能密度對應的疲勞損傷)，根據改進應變能密度法預測得到的車架焊縫主要熱點B、C、D點疲勞壽命大約為13個月左右；而根據傳統應變能密度法計算得到的總應變能密度約為0.911 MJ/m3，對應的疲勞壽命大約為6 012周次，考慮滿載水平路面工況造成的損傷，計算疲勞壽命相當于15個月左右。而車架焊縫實際開裂時間為8個月左右，顯然，基于改進應變能密度法的預測結果與車架焊縫實際開裂時間更加接近，進一步說明了該方法的有效性。基于改進應變能密度法的預測結果比車架焊縫實際開裂時間要保守，這可能是因為電動輪自卸車實際運行路面要比多體動力學仿真分析計算的路面工況更加惡劣，以至于惡劣工況下車架承受的實際載荷更大。

5 結論

(1)本文針對復雜載荷作用下焊接結構應力應變響應出現非完全封閉而交叉的現象，提出了一種改進的應變能密度計算方法，為電動輪自卸車車架焊縫疲勞壽命預測提供理論參考。

(2)通過設計焊接接頭試驗試件進而開展試驗研究，得到焊縫的機械性能和疲勞性能參數，并構建應變能密度疲勞損傷模型，從而為車架多載荷步非線性有限元模擬所需要的材料參數提供可靠而有效的數據基礎。

(3)建立電動輪自卸車車架有限元模型，在其有效性得到驗證的基礎上，等效車架隨機載荷譜，考慮油氣懸架非線性剛度特性，開展多載荷步非線性有限元分析，獲得滿載水平路面和下坡轉彎制動路面兩種工況下的應力應變響應曲線。進而依據改進的應變能密度法計算疲勞損傷參量，并將預測結果與實際開裂位置和失效時間進行對比，發現兩者之間吻合較好，證明了本文方法的有效性。這為開展復雜載荷作用下電動輪自卸車車架焊接結構疲勞壽命預測研究提供了可行的新途徑。