探究過度放縮后的一種 “修正術”
2019-02-15 08:25:42江鳳華江國榮
數理化解題研究 2019年1期
江鳳華 江國榮
(1.江蘇省無錫市輔仁高級中學高三9班 214123; 2.江蘇省無錫市市北高級中學 214045)
一、探究過程
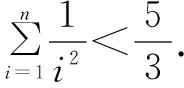

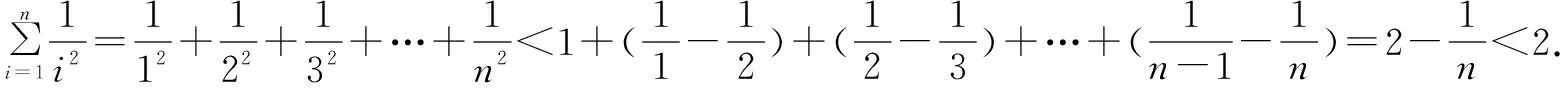
結果發現放縮過度,原因是每一步放縮的“步幅”大了,減小“步幅”后再試.
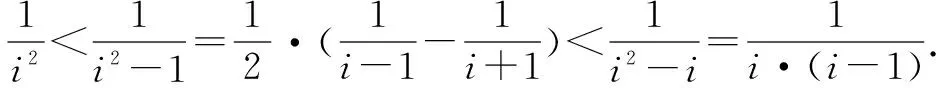


下面筆者做進一步探究:
試證3 若保留前兩項不放縮(易先證明n=1,n=2滿足條件),當n≥3時,
初探感受:(試證3)中通過保留兩項,減少放縮項數,起到了一定的縮小性調節作用,受此啟發,對(試證1)也進行逐步留項探究: 如果保留前兩項不放縮,
分別再保留前三、前四、前五項不放縮,結果依次為:
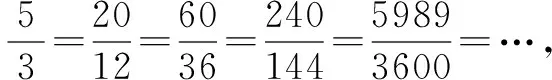
二、小結:根據傅立葉級數展開式
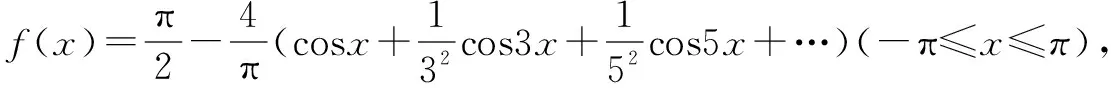
筆者認為:證明此類收斂性數列求和不等式,所證明的目標如果與無窮級數的和有一定的距離的話,若找到了一種可求數列和的放縮方法,即使發現放縮過度(包括放大過度和縮小過度)了,也可在不改變原來的方法基礎上采取逐步保留前幾項不放縮(相當于增加保真項)的辦法減小偏差,這種探求證明過程筆者稱其為順藤留瓜,瓜不熟不摘式,留項累加后再放縮法.
三、方法應用對比舉例
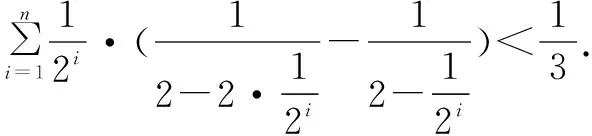



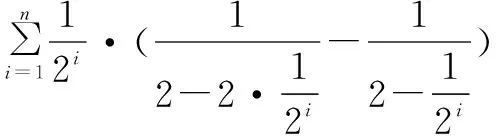
猜你喜歡
中學生數理化·七年級數學人教版(2022年5期)2022-06-05 07:51:48
中等數學(2021年11期)2021-02-12 05:11:46
今日農業(2019年14期)2019-09-18 01:21:42
兒童故事畫報(2019年5期)2019-05-26 14:26:14
快樂語文(2018年13期)2018-06-11 01:18:16
中等數學(2018年11期)2018-02-16 07:47:42
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12
小雪花·成長指南(2015年4期)2015-05-19 14:47:56

