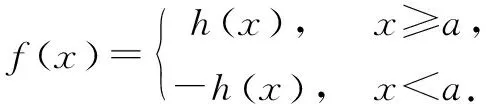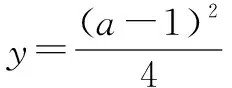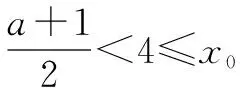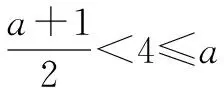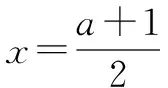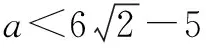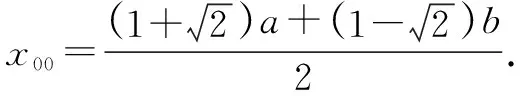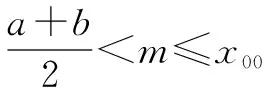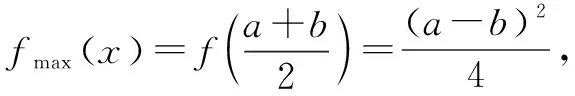f(x)=(x-b)|x-a|型函數性質
2019-02-15 08:22:18孫添耀
數理化解題研究 2019年1期
孫添耀
(浙江省寧波市五鄉中學 315111)
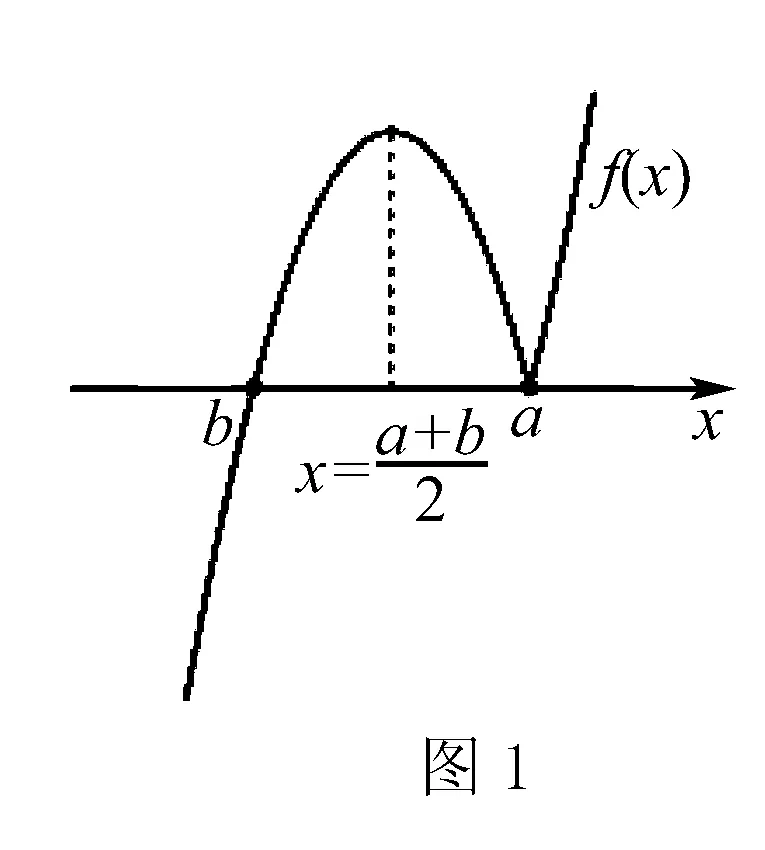
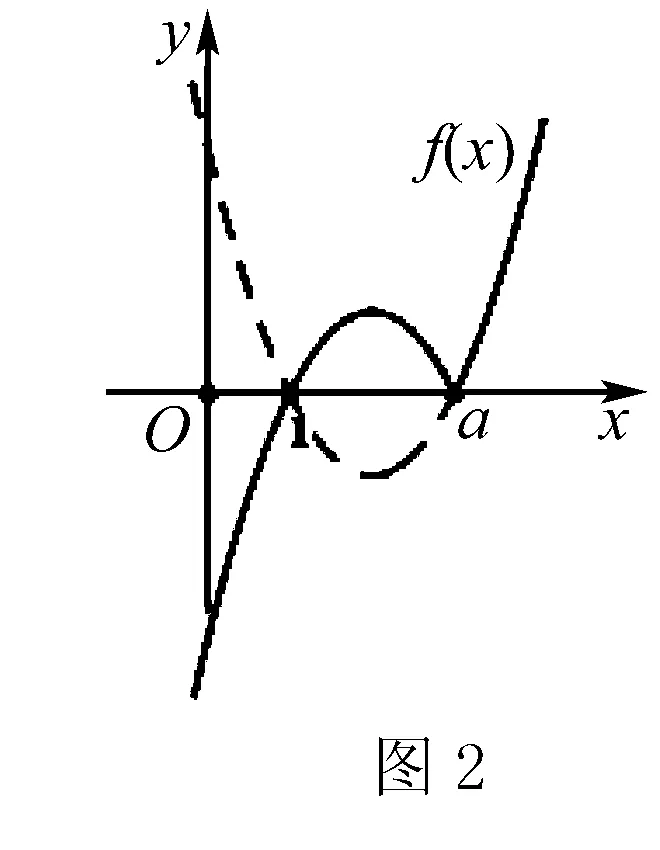
首先研究函數f(x)=(x-b)|x-a|的對稱性與單調性.為了研究方便,不妨固定參數b.且討論a>b時,函數f(x)圖象如右圖1:
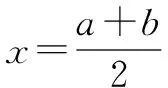
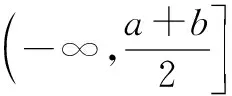
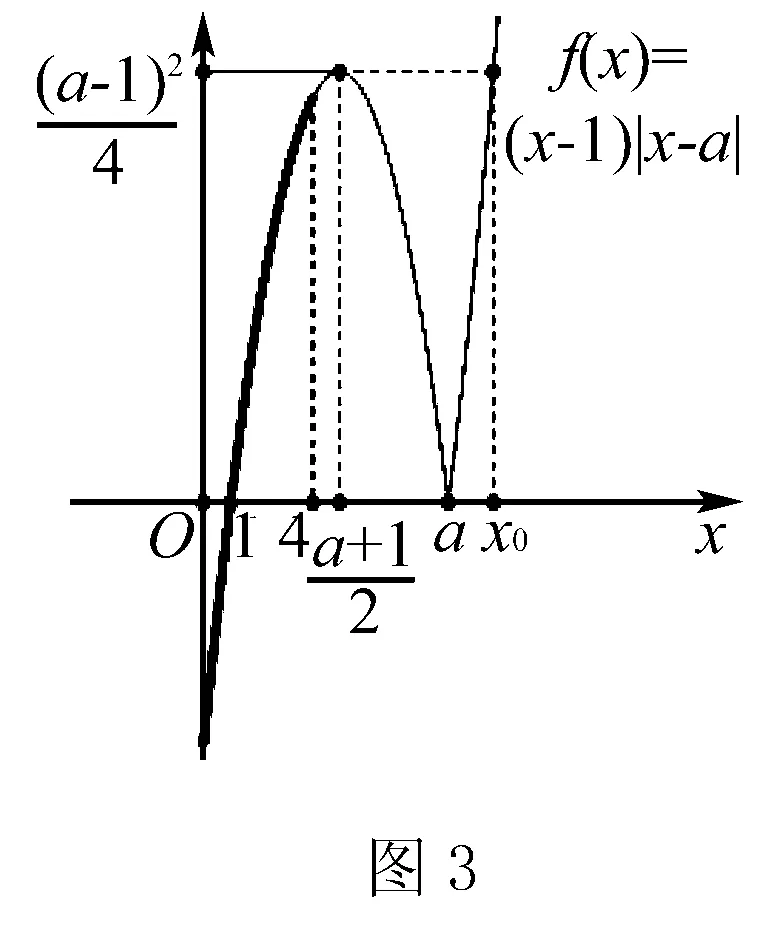
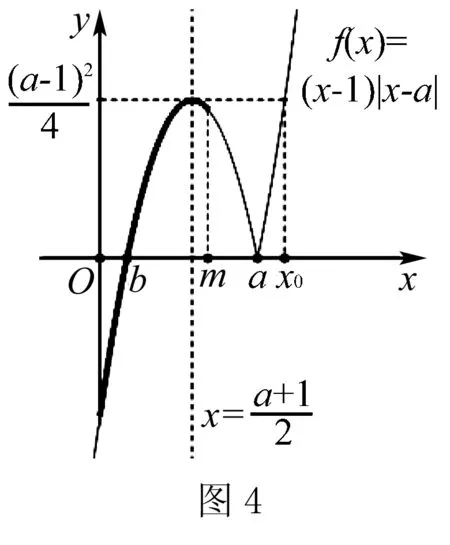
當a 接下來我們討論a>b時函數f(x)在閉區間[0,m]上最值的問題. 不妨令b=1,m=4.求函數f(x)=(x-1)|x-a|(a>1)在區間[0,4]上的最值. 解設原函數為h(x)=(x-1)(x-a)(a>1), 根據函數對稱性作圖2. ∴fmax(x)=f(4)=3|4-a|=3(a-4). 故綜上可得, 一般函數f(x)=(x-b)|x-a|(a>b>0)圖象如圖4. 在區間[0,m]上的最值作如下總結: 此時fmin(x)=f(0)=-ab. 同樣要分成三種情況: ∴fmax(x)=f(m)=(m-b)(a-m) ③當m>x00時, ∴fmax(x)=f(m)=(m-b)(m-a). 故綜上可得,fmin(x)=-ab,