基于貝葉斯網絡的頁巖氣集輸管道失效概率計算方法研究*

魏亞榮，李長俊，吳 瑕

(西南石油大學 石油與天然氣工程學院，四川 成都610500)

0 引言

我國是世界上頁巖氣探明儲量最多的國家，對頁巖氣集輸管道進行失效概率評價，對于保障頁巖氣高效穩定開發具有十分重要的意義。頁巖氣集輸管道運行壓力衰減較快，投產半年后壓力可衰減至投產初期的1/3，甚至更低，且在不同生產階段內管道出砂量也顯著不同[1-4]，這將導致管道承壓情況、應力狀態、沖蝕速率等均隨時間不斷變化，進而引起失效概率的動態變化。傳統的管道失效概率評價方法，如故障樹、失效數據庫模型等均為靜態評價方法，其計算結果不能根據實際情況進行實時更新[5-7]，難以適應頁巖氣集輸管道失效概率動態變化的特點。

貝葉斯網絡是圖論和概率論的結合體，其靈活的網絡布局和概率調節機制可支持風險因素不斷變化的系統進行失效概率分析。Li等[8]利用貝葉斯網絡處理不確定性問題的優勢，動態計算了海底管道失效概率；Khakzad等[9]通過改變貝葉斯網絡節點的概率分布，分析了不同工藝設備的風險事件發生概率的波動情況。但是，目前尚少有學者將該方法應用于頁巖氣集輸管道失效概率研究中。

本文利用失效故障樹和貝葉斯網絡的結構映射關系，建立了頁巖氣集輸管道失效概率計算模型；基于貝葉斯網絡參數學習的過程，完成了模型求解；應用實例驗證了該模型計算頁巖氣集輸管道失效概率的有效性，并可通過調整風險事件的概率分布和狀態，更新管道失效概率。

1 貝葉斯網絡

1.1 基本概念

貝葉斯網絡是基于圖論和概率論的有向無環圖，用來表示1組隨機變量間的依賴關系和概率分布，由節點、有向邊和概率組成[10]。圖1給出了1個簡單的貝葉斯網絡結構圖。

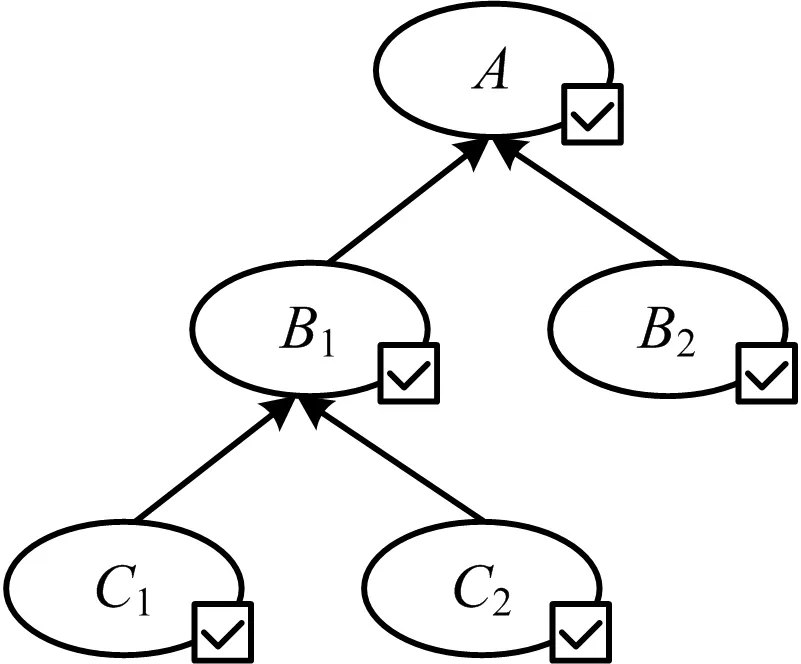
圖1 簡單的貝葉斯網絡示意Fig.1 Schematic diagram of a simple Bayesian network

圖1中，C1，C2，B1，B2，A代表1組隨機變量，箭頭表示隨機變量的依賴關系，C1指向B1，表示C1是B1父節點，B1是C1的子節點；C1，C2沒有父節點指入，因此叫做根節點，根節點有對應的先驗概率分布，非根節點有對應的條件概率分布。

貝葉斯網絡通過式(1)來計算系統的失效概率[11]：

(1)

式中：Pa(Xi)為Xi父節點發生概率；P(Xi|Pa(Xi))為Xi父節點發生條件下子節點發生的條件概率值；P(U)為研究系統的失效概率值。

1.2 貝葉斯網絡處理不確定性問題的優勢

貝葉斯網絡可以通過調整節點的概率分布，更新系統的失效概率值。以圖1為例，分析貝葉斯網絡節點概率分布的調整過程。假設在t1時刻，節點C1發生引起B1發生的概率為0.3；節點C2發生引起B1發生的概率為0.4；C1，C2皆發生引起B1發生的概率為0.6；C1，C2皆不發生情況下B1發生的概率為0.1；則B1節點對應的條件概率分布如表1所示。若在t2時刻，由于外界環境的變化或者研究對象自身的變化，造成節點C1，C2這2個事件的4種發生組合分別引發B1事件發生的條件概率出現波動，針對這種情況，只需在條件概率表1中修改對應的數值即可。

表1 節點B1對應的條件概率表Table 1 Table of conditional probabilities for node B1

貝葉斯網絡可以描述事件的多態性。以管道“腐蝕”風險事件為例，以失效故障樹為代表的傳統方法只能刻畫管道“腐蝕”這一事件的2種狀態，即“存在腐蝕”和“不存在腐蝕”；而工程實際中，管道的腐蝕往往呈現出多種多樣的狀態，貝葉斯網絡可以有效地化解這一矛盾，將“腐蝕”事件描述為如“強腐蝕”、“中腐蝕”、“弱腐蝕”以及“不腐蝕”等多種狀態 。

通過分析可以看出，貝葉斯網絡處理不確定性問題的優勢，可以有針對性地應用于頁巖氣集輸管道因運行工況變化導致的管道風險事件概率不斷變化問題。

1.3 貝葉斯網絡結構建立

網絡結構的建立是運用貝葉斯方法的“瓶頸”，文獻 [12-13]研究發現，失效故障樹和貝葉斯網絡結構具有先天相似性，且故障樹的演繹推理功能可快速確定事件間的依賴關系。因此，可以利用二者之間的映射關系建立貝葉斯網絡。現以失效故障樹的“或”門為例，說明失效故障樹與貝葉斯網絡的映射關系。故障樹或門向貝葉斯網絡轉化示意圖如圖2所示。

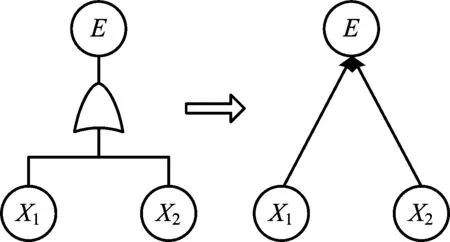
圖2 故障樹“或”門向貝葉斯網絡轉化示意Fig.2 Schematic diagram of a fault tree “or” Gated Bayesian network transformation

圖2中，故障樹中的事件轉化為貝葉斯網絡的節點，邏輯符號直接轉化為有向邊，節點間的依賴關系用條件概率表表示，如表2所示。

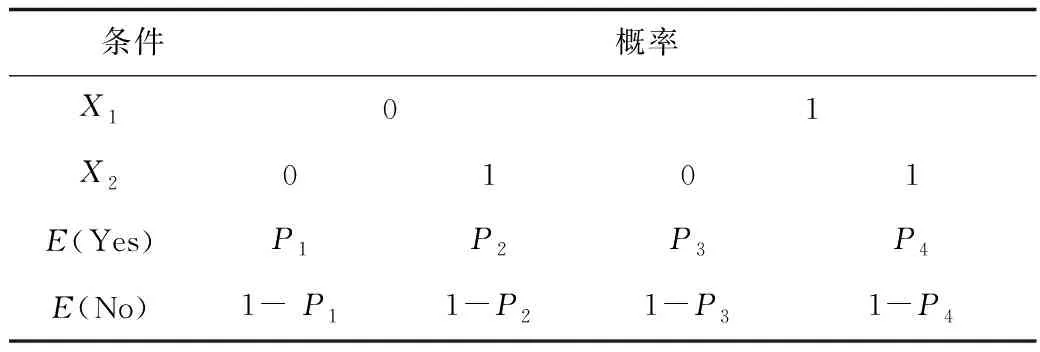
表2 節點E對應的條件概率表Table 2 Table of conditional probabilities for node E

2 基于貝葉斯網絡的頁巖氣集輸管道失效概率模型

2.1 頁巖氣集輸管道失效故障樹

歐洲天然氣管道事故組織(EGIG)的數據顯示，腐蝕、第三方破壞、誤操作、設計與施工缺陷、自然災害等是造成天然氣管道失效的主要原因，而頁巖氣集輸管道受運行工況的影響，管道內沖砂磨損比較明顯。因此，引入“管道內含有沖蝕物”這一風險事件。在此基礎上，分析頁巖氣氣質特征，并利用故障樹演繹推理的能力，建立頁巖氣集輸管道失效故障樹，如圖3所示。故障樹中的符號各自對應的事件如表3所示。

2.2 失效故障樹向貝葉斯網絡轉化

根據失效故障樹與貝葉斯網絡之間的結構映射關系，將失效故障樹轉化成貝葉斯網絡，轉化結果如圖4所示。從圖4可以看出，X1～X36為根節點，其余為非根節點。

2.3 模型求解

模型求解就是貝葉斯網絡參數學習的過程，包括如下幾個步驟[14]：

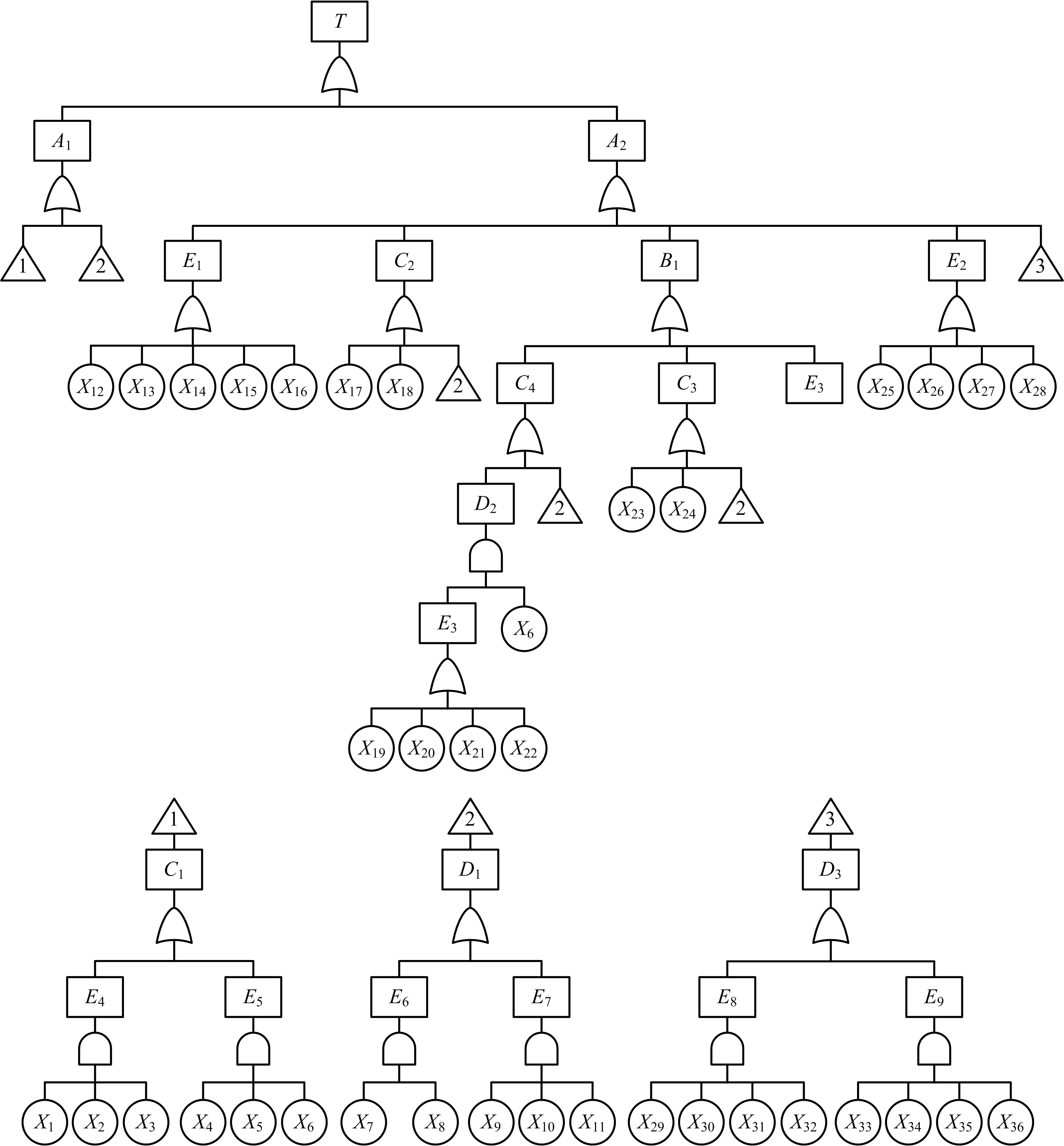
圖3 頁巖氣集輸管道失效故障樹Fig.3 Failure tree of shale gas gathering pipeline

符號事件符號事件符號事件A1穿孔X1土壤腐蝕X20管段存在應力集中A2開裂X2陰極保護失效X21外界存在較大作用力B1管線腐蝕開裂X3防腐絕緣層失效X22管線內應力較大C1管線腐蝕嚴重X4管線抗腐蝕性能差X23管線機械性能差C2管線承壓能力低X5輸送介質中含腐蝕物X24管線抗腐蝕性能差C3管線存在裂紋X6輸送介質中含沖蝕物X25水毀發生C4管線力學性能差X7制造缺陷X26泥石流發生D1管道存在缺陷X8材料缺陷X27洪水發生D2管線應力腐蝕嚴重X9安裝不當X28滑坡發生D3誤操作X10機械損傷X29規程與作業指導有誤E1第三方破壞嚴重X11存在違章建筑物X30SCADA通信系統問題E2地質災害X12土層遠移X31安全設備問題E3管線承載過大X13管線標注不明X32操作人員失誤E4管線外腐蝕X14壓管嚴重X33維護方式不當E5管線內腐蝕X15上方違章施工X34維護人員責任心不強E6管線存在初始缺陷X16焊接不當X35維護設備差E7管線存在施工缺陷X17管線抗腐蝕性能差X36維護文件資料缺失E8運營誤操作X18管線設計不合理E9維護誤操作X19管段存在殘余應力

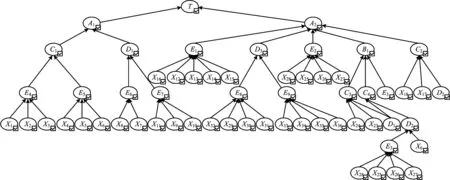
圖4 頁巖氣集輸管道失效概率分析的貝葉斯網絡Fig.4 Bayesian Network for failure probability analysis of shale gas gathering pipelines

1)確定36個根節點的先驗概率和非根節點的條件概率。這些概率值可以通過分析和整理管道的歷史失效數據獲得；當歷史失效數據保存不完善時，一般采用專家估計和模糊理論相結合的方法來確定[15]。

2)基于獲得的節點概率信息，利用貝葉斯網絡的計算軟件，計算管道失效的概率值，即完成貝葉斯網絡預測推理功能。

3)將頁巖氣集輸管道失效概率值設置為1，運用貝葉斯網絡診斷推理功能，找到影響管道失效的關鍵風險因素。

4)根據管道的實際情況，調整風險節點的概率分布或存在狀態，更新管道的失效概率值。

3 實例應用

3.1 管道基本信息

某頁巖氣氣田的某條采氣管道在2015年2月投產，管線設計規模為48×104m3/d，設計壓力為8.5 MPa，管材規格為D168.3×6.3/7.1 L245N 無縫鋼管，管線設計長度為2.87 km，沿線穿越丘陵，且經過二級地區和三級地區，利用建立的基于貝葉斯網絡的頁巖氣集輸管道失效概率模型計算其失效概率值。

3.2 管道失效概率計算

1)通過分析該條管道的失效記錄，并結合專家估計信息，確定了投產3 a后的管道風險事件的概率分布，計算結果如表4～7所示。鑒于非根節點的數量較多，文中不再一一給出。

2)根據節點參數，利用匹斯堡大學開發的開放式貝葉斯網絡模擬軟件GeNIe 2.0，計算得到該條管道在投產3 a后的失效概率值為6.32×10-2次/(km·a)。

表4 根節點的先驗概率值Table 4 The prior probability value of the root node 次/(km·a)

表5 節點D2對應的條件概率表Table 5 Table of conditional probabilities for node D2

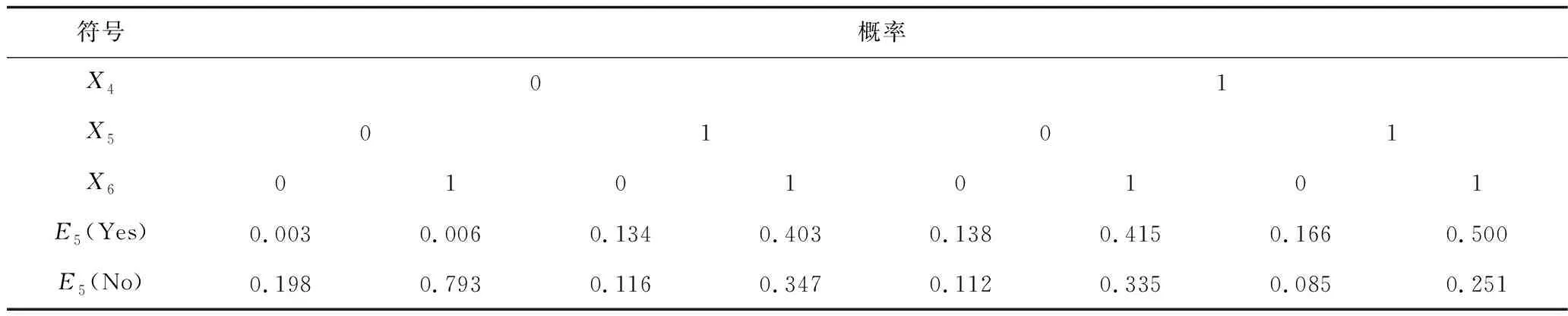
表6 節點E5對應的條件概率表Table 6 Table of conditional probabilities for node E5

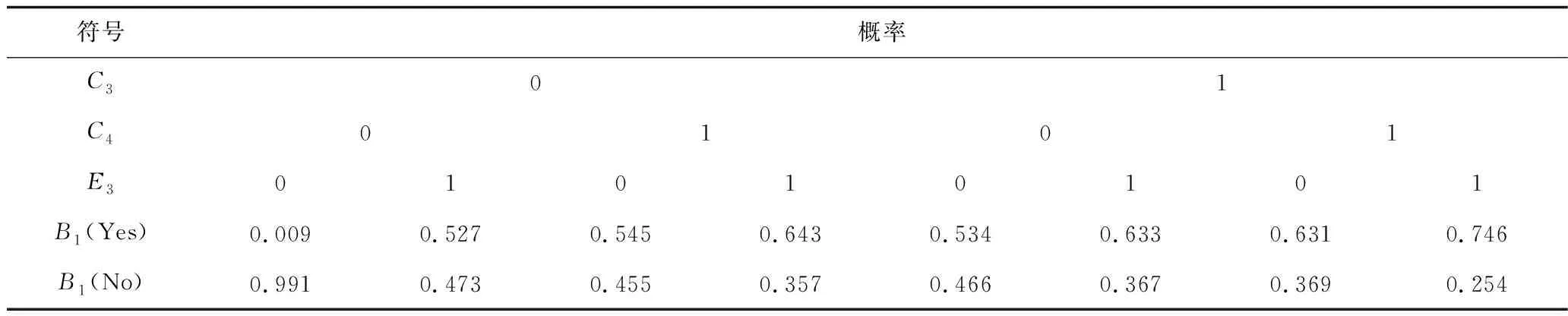
表7 節點B1對應的條件概率表Table 7 ATable of conditional probabilities corresponding to node B1

3)將管道的失效概率值設置為1，利用GeNIe軟件確定根節點發生概率的相對大小，對36個風險事件按發生概率大小排列，結果為：X6>X5>X2>X3>X1>X15=X34>X10>X29>X23=X32>X12=X35>X28>X20=X21=X22=X36>X5=X9=X11=X18>X16=X33>X19=X17>X13>X30>X14>X31=X4>X7=X8>X24=X25=X26=X27。從計算結果可以看出，控制管道沖蝕風險事件和腐蝕風險事件的發生可最有效地降低管道失效概率值。

3.3 管道失效概率更新

利用貝葉斯網絡處理不確定問題的優勢，來預測管道投產4 a的失效概率值。

1)調整X6和B1等節點的概率分布。針對X6，即“輸送介質中含沖蝕物”這一風險事件，根據頁巖氣集輸管道運行工況的變化規律，投產初期，壓力高且含砂量大，砂粒隨氣流高速運行對管道內壁造成的沖蝕磨損嚴重，隨壓力衰減，沖蝕磨損降低，基于此，并結合專家估計信息，將該事件發生概率由原來的6.6×10-3次/(km·a) 調整為4.7×10-3次/(km·a) ；相應地，隨投產時間延長，調整B1的條件概率分布，調整結果如表8所示，其余節點的變動不再一一給出。

2)調整E5節點的存在狀態。隨投產時間延長，管道腐蝕狀態呈現多樣性，因此將“管線內腐蝕”(E5)的狀態由原來的“腐蝕”和“不腐蝕”2種修正為“強腐蝕”、“弱腐蝕”和“不腐蝕”3種，修正結果如表9所示。

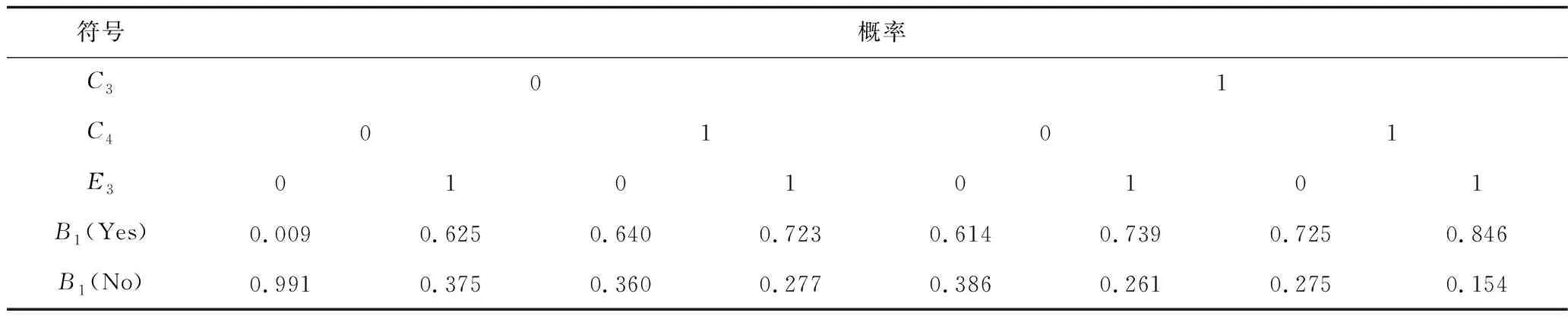
表8 節點B1調整后的條件概率表Table 8 The conditional probabilityTable after the B1 adjustment of the node

表9 E5對應的條件概率表Table 9 Table of conditional probabilities corresponding to node E5

3)利用GeNIe軟件計算得到該條管道在投產時間為4 a時的失效概率值是6.89×10-2次/(km·a)。

4 結論

1)將貝葉斯網絡方法與失效故障樹結合使用，能夠快速確定風險因素間的因果關系，打破了貝葉斯網絡方法應用的“瓶頸”，而貝葉斯網絡處理不確定性問題的優勢可有效地克服傳統靜態失效概率計算方法的弊端，為頁巖氣集輸管道失效概率預測提供了技術支撐。

2)應用實例表明，基于貝葉斯網絡的頁巖氣集輸管道失效概率模型既可計算頁巖氣集輸管道的失效概率值，又能確定影響管道失效的關鍵風險因素，并且針對管道運行工況及投產時間的不斷變化，可通過調整網絡節點的概率分布和狀態，實現頁巖氣集輸管道失效概率的更新。