基于GM-SVR的小樣本條件下化工設備可靠性預測*

趙江平，丁 潔，陳敬龍

(西安建筑科技大學 資源工程學院，陜西 西安 710055)

0 引言

化工企業的生產特點決定了化工設備可靠性的重要性，準確預測設備可靠性趨勢，制定合理的預防性維修計劃，才能保障設備長期穩定運行[1]。對化工設備進行可靠性分析時，大多數學者采用威布爾分布模型來描述化工設備的壽命。裴峻峰等[2]將威布爾分布應用于往復式壓縮機壽命建模，對壓縮機維修周期進行了分析；徐子軍[3]使用威布爾分布擬合離心泵各單元故障分布，預測了離心泵系統可靠性。但前者所研究的內容都是基于樣本數據足夠豐富，而在化工企業實際生產運行中，數據樣本常常呈現出小樣本的特征，且較少有人將小樣本數據分析方法應用到化工設備的可靠性評估中。因此，小樣本條件下的化工設備壽命分布及可靠性預測存在很大的困難。

對小樣本數據分析的研究在機械、航空等行業已有大量研究。宋明順等[4]采用灰色估計法與貝葉斯方法對小樣本機械系統進行可靠性估計；金星等[5]通過蒙特卡羅模擬對小樣本條件下的近似服從威布爾分布的設備壽命進行了評估；馬憲民等[6]使用粒子群算法估計了礦用減速器可靠性壽命。但大量的研究表明，以上方法都或多或少有其應用的局限性。Bayes方法受驗前信息影響較大；應用蒙特卡羅模擬法的前提是必須要保證現場數據樣本服從的分布模型是高度精確的[7]；粒子群算法和灰色估計法在小樣本的情況下預測精度不高。所以當故障樣本為小樣本時，通過建立化工設備可靠性模型，研究1種精度較高的參數估計方法，對于預測設備可靠性非常重要。

近年來，支持向量機(SVM)作為1種高度適用于小樣本情況的機器學習規律理論，在兩參數威布爾分布參數的估計中得到了廣泛的應用[8]。支持向量回歸(SVR)在SVM的基礎上引入了損失函數，使支持向量機的應用拓展到了回歸分析的領域。由于SVR具備SVM適合于小樣本數據的特點，即同樣適合于對歷史故障數據積累不足的化工設備可靠性分析。此外，雖然灰色估計法的預測精度不高，但研究表明其在小樣本數據下可以獲得精度較高的位置參數估計值，故可通過GM(1，1)模型將三參數威布爾分布的參數估計轉化為兩參數威布爾分布的參數估計問題[9]。本文以某化工企業壓縮機投運以來的部分故障數據為實例，建立了三參數威布爾模型，用GM(1，1)和SVR對威布爾分布參數進行估計，并與單獨使用灰色估計法及最小二乘法的估計結果進行對比，以此來驗證GM-SVR模型參數估計在化工設備可靠性預測中的有效性。

1 化工機械設備可靠性模型

1.1 小樣本失效數據

在化工企業生產運行期間，隨著科學技術不斷發展，化工設備更新換代速度快，許多設備在短周期運行中根本沒有發生故障，這使得同型號設備的故障數據更少；此外，由于企業管理的不足，我國不少化工企業(尤其是中小型企業)的維修報告、調度中心運行報告、臺賬系統等記錄表易出現缺失的情況，導致積累的故障維修歷史數據不足。綜上所述，對在役化工設備維修情況調研獲得的故障壽命數據極有可能呈現出比較典型的小樣本特征。

1.2 威布爾分布模型

威布爾分布函數是由物理學家Weibull在研究鏈的強度中提出的1種分布函數，在工程應用中常用來擬合機械、電子、化工等設備的壽命分布。三參數威布爾分布模型的分布函數F(t)和失效率函數λ(t)的表達式分別為[10]：

(1)

(2)

式中：t為失效時間,h；η為尺度參數，η>0；m為形狀參數，m>0；r為位置參數。形狀參數m的取值大小不同，則對應的設備失效類型也不同。當m<1時，為早期故障期，隨著設備的持續運行，失效率逐漸降低，設備的可靠性程度越來越高；當m=1時，設備處于偶然故障期，此時的失效率是1個常數，即此時的失效率服從指數分布；當m>1時，設備處于耗損故障期，隨著運行時間的增加，設備逐漸出現老化和劣化。由此可見，威布爾分布可以很好地描述各種失效模式，故可以使用三參數威布爾分布作為化工機械設備的失效分布函數，可靠度函數R(t)為[10]：

(3)

2 威布爾分布模型的參數估計

為了能夠準確獲得某個設備的失效率模型，根據該設備運行中產生的故障樣本數據建立威布爾分布模型。具體實現方法是用平均秩次法或中位秩法計算出F(ti)，采用相關系數優化法計算三參數威布爾分布的位置參數r，再將威布爾分布模型線性化，然后采用擬合方法識別分布參數。目前的參數估計方法有灰色估計法、最小二乘法、極大似然估計法等方法。但這些方法對于小樣本參數估計的精度不高。灰色估計法在小樣本的情形下對形狀參數m和尺度參數η的估計精度不高，但是對位置參數r的估計精度較高。故本文先使用GM(1，1)模型對位置參數r進行求解，在r已知的基礎上，再利用SVR估計形狀參數m和尺度參數η。

2.1 經驗分布函數

在對威布爾分布參數進行回歸分析時，必須計算樣本的經驗分布函數。設某化工設備失效樣本數量為n，失效樣本的運行時間分別為t1≤t2≤≤tn(完全樣本)，相應的累計失效概率(經驗分布函數)為F(t1)≤F(t2)≤≤F(tn)，當數據樣本為小樣本時，工程上常使用中位秩公式或平均秩次法對第i個產品的累計失效概率F(ti)進行計算[11]。

平均秩公式為：

(4)

中位秩公式為：

(5)

2.2 基于GM(1，1)的位置參數估計

灰色GM(1，1)模型主要用于復雜系統某一主導因素特征值的擬合和預測，預測過程中所需信息較少，迭代快，精度高。在化工設備運行過程中，引起其失效的因素有很多，這使得可靠性預測和風險研究存在一定的灰色問題，這種情況下，可以依據故障數據建立灰色預測模型。灰色GM(1，1)模型的微分方程為[12]：

(6)

對式(6)進行變形可得：

(7)

令

則式(7)變形為：

xi=b+cexp(-aτi)

(8)

將(xi,τi)視為一般時間序列，灰色GM(1，1)的時間響應模型為：

(9)

式(6)與式(9)具有相似性，則通過一次對GM(1，1)模型的求解，即可得到參數a，u，c的估計值，使用最小二乘法計算灰色模型的參數：

(10)

式中：

(11)

由于本文所研究的故障樣本較少，尺度參數η和形狀參數m的估計效果一般，故只保留位置參數r的估計值，并應用支持向量機對η和m進行估計，令t=x-r，式(1)變形為兩參數威布爾分布：

(12)

2.3 基于支持向量機的參數估計

2.3.1 威布爾分布模型線性化

分別對等式(12)兩端取2次對數得：

(13)

令

(14)

式(13)可以簡化為y=wx+b，對參數η和m的估計轉化為對參數w和b的估計。如果把x和y看作SVR模型中的訓練樣本，T={(xi,yi)}；i為樣本序號；n為樣本數量；i=1,2,,n；xi為輸入變量；yi為相應的系統輸出變量，就可以使用SVR對其進行回歸分析。

2.3.2ε-支持向量回歸機方法

ε-支持向量機估計回歸函數(ε-SVR)是通過引入ε線性不敏感損失函數，將回歸問題轉化為最小化結構風險函數的問題。即尋找1個使風險最小的最優超平面f(x)=wφ(x)+b=0，w為權值系數，b為偏差，φ(x)為非線性映射[13]。

為了使f(x)平坦，引入松弛變量ξi，ξi*和懲罰參數C建立優化模型如下[14]：

(15)

由于高維空間的內積運算極其復雜，引入核函數k(xi,yi)來替代內積運算。對于線性樣本，本文采用線性核函數k(x,y)=x·y作為訓練核函數。式(15)是凸二次規劃問題，求解該優化問題是通過求解它的Lagrange對偶問題而得到的。引入Lagrange函數構造并求解[15]：

(16)

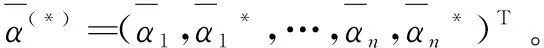
2.3.3 參數選擇

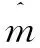
(17)

2.3.4 誤差分析

為了驗證模型的擬合精度，有必要對數據的擬合效果進行誤差分析。本文使用相對均方根誤差(NRSME)及擬合優度(R2)對數據擬合效果進行誤差分析[17]。

相對均方根誤差的計算公式為：

(18)

擬合優度(R2)的計算公式為：

(19)

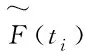
3 分析案例

由于某化工企業進行了搬遷，導致某壓縮機機組部分運行的臺賬及設備維修記錄丟失。不考慮預防性維修，只對泄漏、停機、斷裂等嚴重影響設備運行的故障進行統計。收集到10臺同型號的壓縮機故障數據如表1所示，將其故障時間數據(完全樣本數據)按從小到大的順序排列，假定該組故障時間數據服從三參數威布爾分布，采用式(4)和式(5)計算各失效時間點對應的累計失效概率，記于表1中。

將失效時間ti及其對應的累計失效概率F(ti)作為GM-SVR模型的2組初始樣本集T1={ti,F1(ti)}和T2={ti,F2(ti)}。使用GM(1，1)模型對初始樣本集進行參數估計，保留位置參數r的估計值，按式(14)對初始樣本集進行處理，分別得到SVR模型的2組訓練樣本集T1′={xi,F1(xi)}和T2′={xi′,F2(xi′)}，將樣本集輸入SVR進行訓練，采用交叉驗證和網格搜索法對擬合過程中的參數進行優化選擇。參數尋優結果及可靠性分布參數估計值如表2所示。

表2中的誤差分析結果表明，2種經驗公式的擬合優度均大于0.98。一般當R2≥0.9時，就可以說明擬合精度較高。由此可見，該組故障數據與中位秩、平均秩

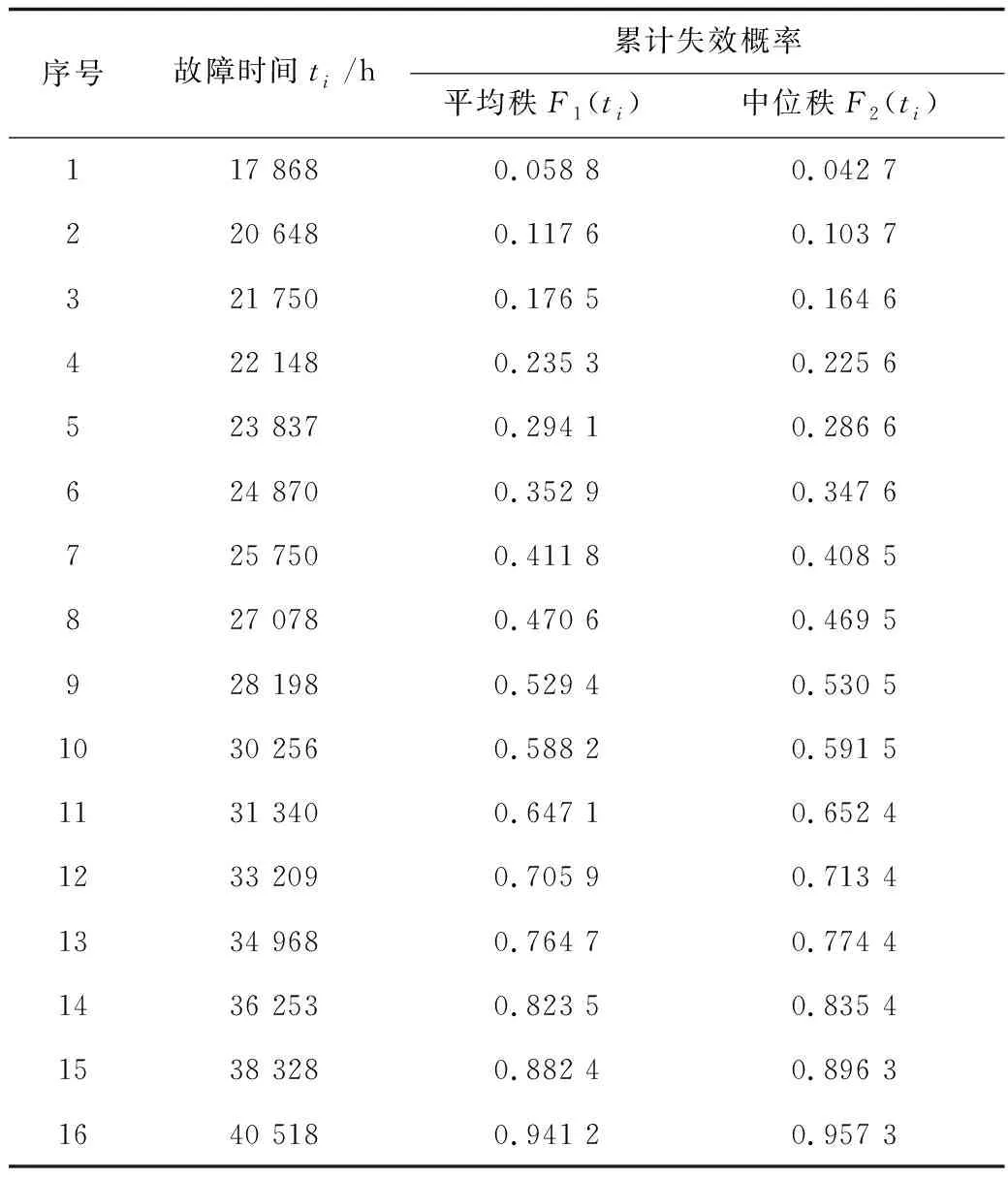
表1 壓縮機故障記錄及其累計失效概率Table 1 Operating record of compressor and cumulative failure probability

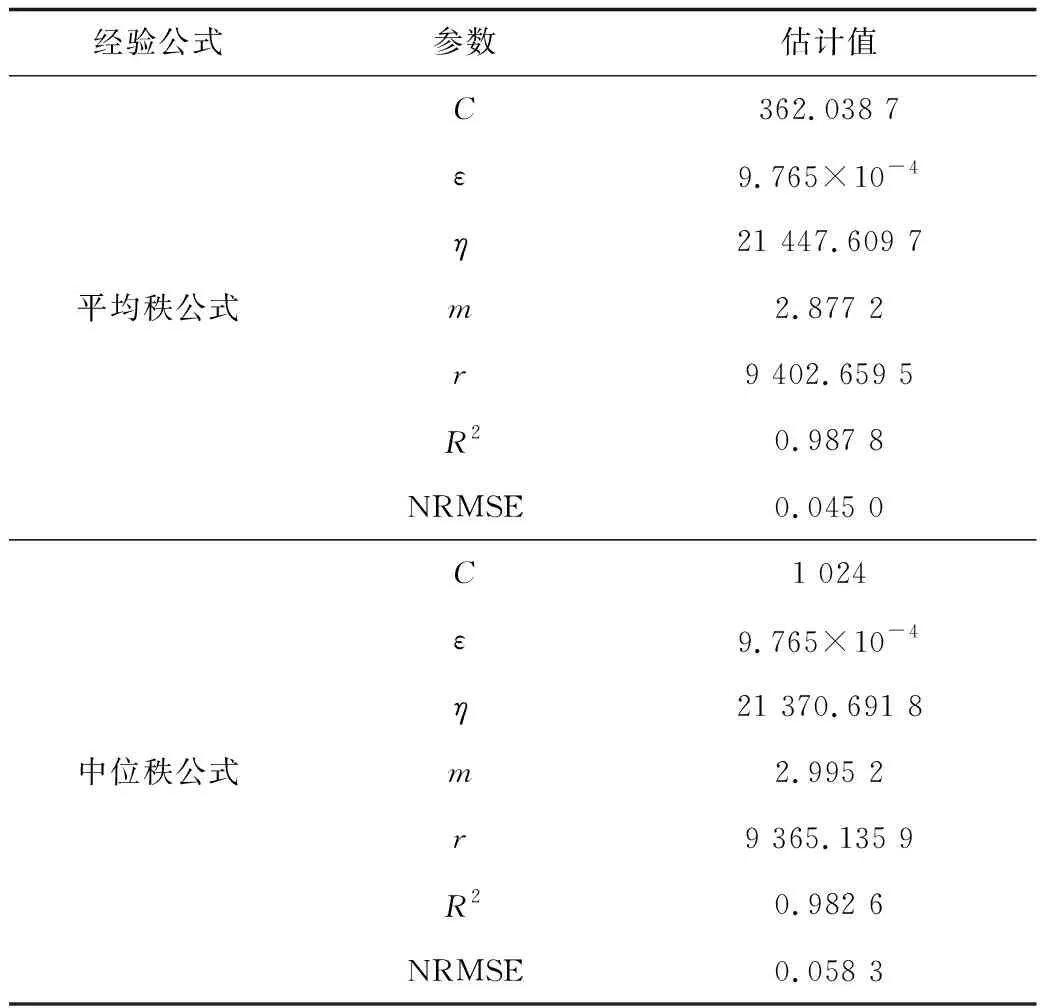
表2 GM-SVR模型估計結果Table 2 Estimation results of GM-SVR

之間存在明顯的線性關系，所以接受該壓縮機失效壽命數據服從三參數威布爾分布的假定。當選擇平均秩公式時，相對均方根誤差及擬合優度均優于中位秩公式，故選擇平均秩公式作為該壓縮機壽命數據的經驗分布函數更合適。

為檢驗GM-SVR模型的有效性，將使用平均秩公式的訓練樣本分別運用最小二乘參數估計法(LSR)、灰色估計法(GM)進行參數估計，計算得出不同方法下的威布爾分布參數估計結果，分別對其進行誤差分析，對比估計效果。估計結果及誤差分析分別如表3、表4所示。

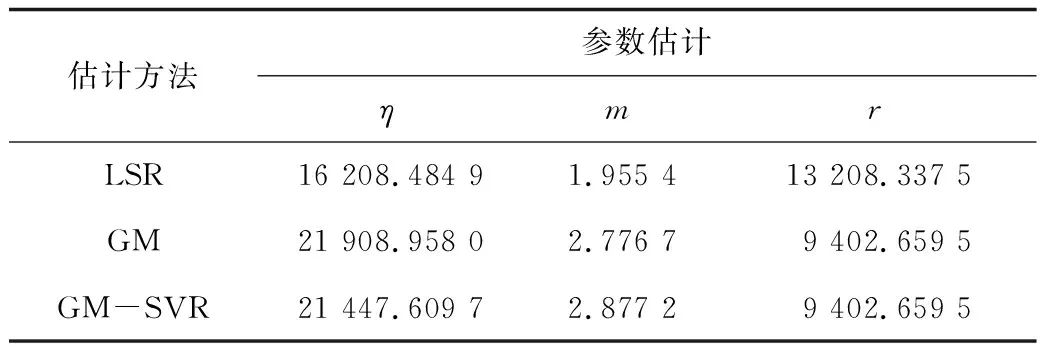
表3 各擬合方法參數估計值Table 3 Estimated results of parameters of each fitting method

表4 各擬合方法誤差分析Table 4 Error analysis of each fitting method

通過表3和表4對比參數估計及誤差分析可以看出，使用灰色估計法和GM-SVR這2種方法所得的尺度參數η和形狀參數m的估計值基本一致。GM-SVR的NRSME值為0.045 0，灰色估計法的誤差為0.050 7，說明GM-SVR可以實現GM(1，1)的參數估計效果，而且精度高于GM(1，1)。由此可見，在小樣本條件下，GM-SVR的參數估計精度有明顯優越性，而LSR是最差的。圖1為3種估計方法的威布爾分布函數與該壓縮機機組平均秩擬合曲線對比圖，從圖1中可以更直觀的看出GM-SVR對整體數據有明顯的擬合優勢，可以有效地應用于小樣本故障數據下的壓縮機可靠性預測。

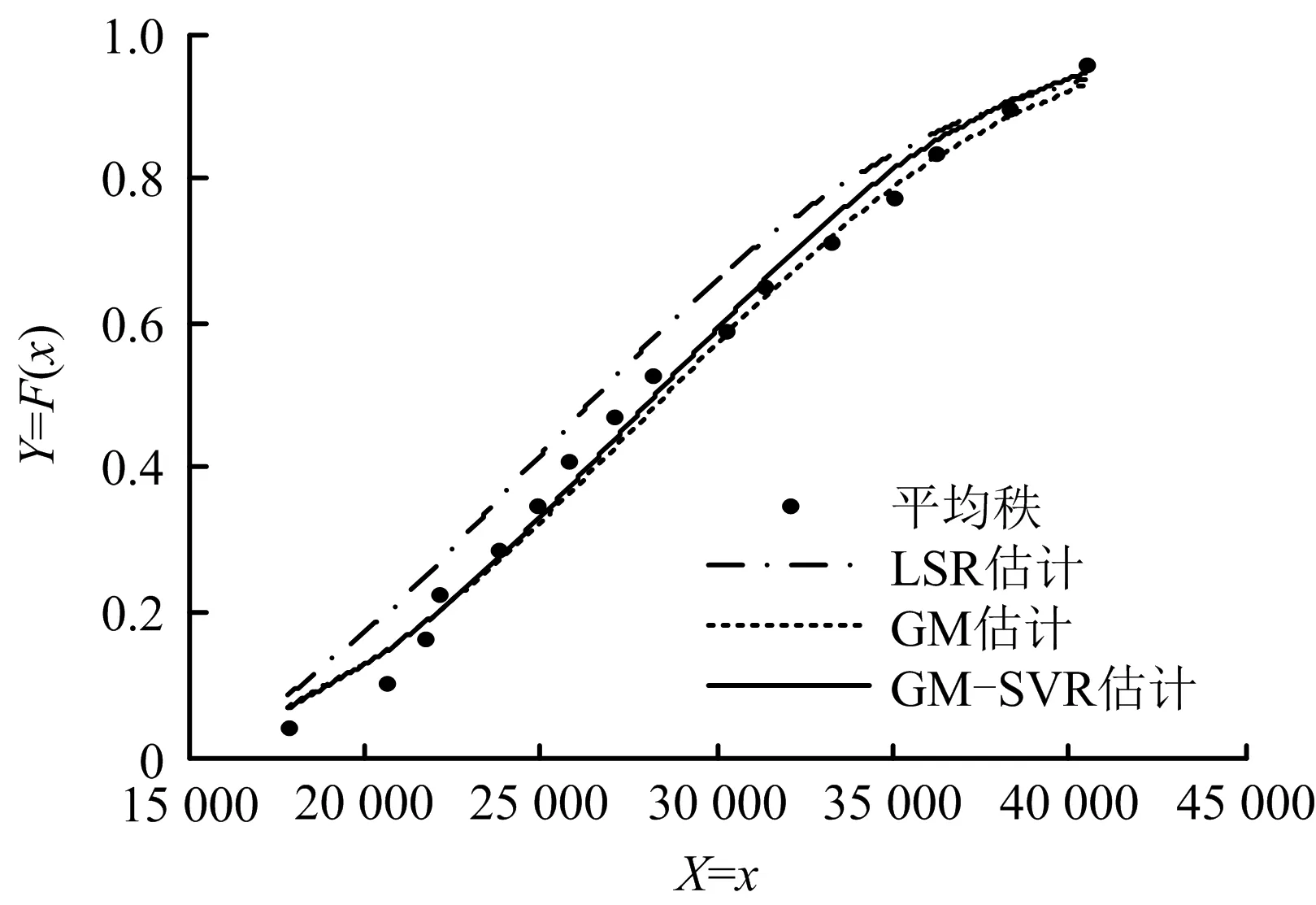
圖1 3種方法的擬合對比Fig.1 Comparison of the three fitting methods

根據式(3)及GM-SVR模型估計參數，可得該組壓縮機可靠度函數為：

通過壓縮機的可靠性模型，可以計算出該型號壓縮機的平均無故障時間為：

由可靠度函數R(t)可以得出該型號壓縮機的動態可靠性曲線，如圖2所示。由圖2可知，可靠度隨著運行時間的增長逐漸下降，當運行了19 118 h后，其可靠度明顯下降。根據可靠性曲線可以預測每個運行時間點的可靠度，本例中，預測設備運行34 177 h后可靠度為22%，企業可根據自身工藝情況對風險的接受程度決定是否采取預防性維修。

圖2 壓縮機動態可靠性曲線Fig.2 Reliability dynamic curve of compressor

4 結論

1)通過實例應用證明，三參數威布爾分布可以用作化工設備的可靠性建模。通過分析故障樣本數據，可以為預測設備可靠度及制定設備維修策略提供依據，同時也為化工企業的風險評估提供數據支持，具有工程應用價值。

2)GM-SVR模型可以有效地應用于小樣本數據條件下的化工機械設備可靠性分析，該方法的估計精度要高于傳統最小二乘估計法和灰色估計法。在參數估計過程中，利用程序實現回歸分析，可以提高參數的估計精度和設備可靠性分析的效率。