基于多周期的危險品多式聯運路徑優化研究*

李 萍,朱宗良,萇道方

(上海海事大學 物流科學與工程研究院，上海 201306)

0 引言

根據國家統計局統計，2017年我國多式聯運貨運量約17.47億t，占全社會貨運量的4.1%，其中危險品多式聯運貨運量約2億t，占比約為16.5%。2020年，我國多式聯運貨運量預計將達到30.28億t，復合增長率為20.11%[1]。危險品貨運量增加的同時，也給危險品運輸帶來了挑戰，研究危險品多式聯運路徑優化問題具有重要意義。

目前，國內外學者對危險品多式聯運已經有了一些研究。魏航等[2]將運輸網絡進行變形,建立了在時變網絡條件下多式聯運有害物品的最短路徑模型，并利用Dijkstra算法求解出不同出發時間下的有效路徑；葉熾球[3]在此基礎上，考慮時變條件對危險品運輸社會恐慌度的影響，構建時變條件下有運量限制的危險品道路運輸最短路徑模型；張得志等[4]建立了時間和路段能力約束的最短路徑模型，并用啟發式算法求得多城市間多種運輸方式的最佳組合；開妍霞等[5]以事故損失及運輸成本線性加權和最小為目標，對危險品運輸網絡中的運輸方式和路徑優化開展研究；黃麗霞等[6]以總成本和總風險最小為目標，建立雙目標0-1線性規劃模型；Xie等[7]研究了危險品多式聯運的選址-路徑問題，建立了1種多目標、多模式的混合整數線性規劃模型；辛春林等[8]以成本和風險的加權和最小化為目標建立了配送選址—多式聯運路徑優化模型;辛春林等[9]基于運輸費用和人口風險的較強時變特性,建立危險品多式聯運的最短路徑選擇模型，利用Dijkstra改進算法進行求解;Manish Verma和Ghazal Assadipour等[10-13]在多式聯運的基礎上，考慮風險因素，建立風險模型。從以上文獻可以看出，關于危險品多式聯運的研究都是使用單周期模型進行終端選址和路徑優化，而危險品運輸具有較強時變的特性，因此本文考慮在動態網絡下，選擇多周期模型進行路徑優化。

本文基于由多個路徑期組成的危險網絡進行規劃研究，以降低運輸成本及風險(傷亡人數及財產損失)為目的，建立1個混合整數概率魯棒模型，并通過模擬退火算法求解，達到在不同場景及周期內多式聯運終端位置和運輸路線同時優化的目的。

1 模型構建

1.1 問題描述

本文研究了危險品多式聯運網絡擴張問題，在網絡規劃期間，某一路徑起止點(Origin Destinatinpair, OD對)之間的運輸路線上可能包含多個多式聯運終端，并將規劃期T劃分為1組短時間段即路徑期，用于路徑決策，同時這些時段的1個子集Tl進行擴張決策，且在每1個擴張期以及在預算范圍內開放新終端，擴容已有終端或者重鋪鐵路。由于受到自然或人為因素的影響，網絡終端和鏈路中斷的風險具有不確定性，且存在發生中斷的概率，這些中斷會很大程度降低終端及鏈路的運輸能力，以及對人口密集且短時間內不易疏散的脆弱區域造成人口傷亡和財產損失，當受影響的終端及鏈路逐漸恢復能力時，其將再次成為最優路徑。多周期的規劃問題可以概括為在每個擴張期預算有限的情況下確定需要改進的路徑期。本文做了以下假設：在每個擴張期開放的終端在規劃期內一直保持開放;擴大終端的容量在規劃期內不會減少;各終端及路徑上的成本和風險已知;各場景下的終端及鏈路中斷風險是相互獨立的;中斷只發生在擴張期，受損的終端及鏈路從路徑期中逐漸恢復，直到下一個擴張期完全恢復。

1.2 符號說明

1)集合含義：

2)參數含義：

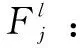
3)決策變量含義：

1.3 模型建立

minC期=μC+(1-μ)R

(1)

(2)

(3)

(4)

s.t.

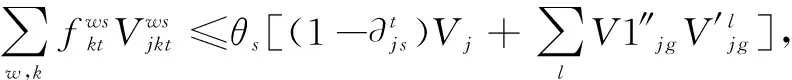
(5)

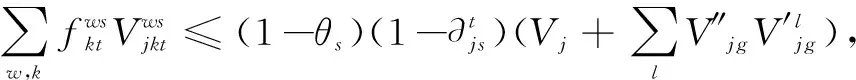
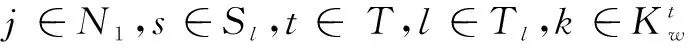
(6)

(7)

(8)

(9)

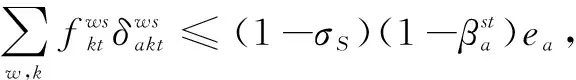
(10)

(11)

(12)

(13)

(14)

(15)

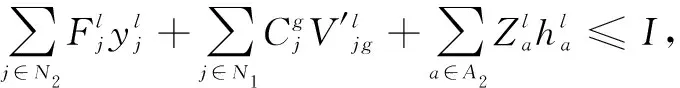
(16)

(17)

式(1)為目標函數,表示期望成本最低，其中μ為運輸危險品的成本權重(假設μ為0.6)，(1-μ)為風險權重；式(2)表示危險品風險函數，包括運輸風險和轉運風險；式(3)表示危險品的成本目標函數，包括開放終端成本，擴容終端容量成本，鐵路重鋪成本，運輸成本和轉運成本；式(4)表示運輸風險，其中β1和β2分別為人口風險和財產風險的權重；式(5)和式(6)表示確保已有終端的容量在所有路徑期內都多于路徑上的貨流；如果終端在以后的特定場景下保持彈性，則激活式(5)，否則使用式(6)；式(7)表示確保危險品在公路中的貨流不超過其鏈路的能力；式(8)表示確保新開放的終端容量在所有路徑期內都多于路徑上的貨流；式(9)和式(10)表示確保危險品在鐵路中的貨流不超過其鏈路的能力，與式(5)和式(6)類似，如果在特定場景下鏈路保持彈性，則式(9)被激活，否則式(10)被激活；式(11)表示確保最多可以為已有終端選擇1個容量模塊;式(12)表示確保備用終端在所有擴張期內最多可以打開1次；同理，式(13)表示保證每條鐵路鏈路在擴展周期內最多進行1次重鋪；式(14)表示確保OD對間的供需平衡；式(15)表示確保貨流分配給開放的終端；式(16)表示在擴張期內成本不能超過預算；式(17)表示決策變量非負。

2 模型求解

1)將可行解編碼為1個單維數組。每個數組由2個部分組成，分別用于尋找備用終端和鐵路重鋪決策以及在擴張期擴容已有終端的容量。通過該算法生成1個隨機初始解，并對其在式(16)條件下的可行性進行驗證，當決策變量確定下來時，問題就變為單一場景單一路徑期下的多式聯運路徑規劃問題。當路徑子問題得到解決時，則開始計算目標函數。

步驟1：選擇1個決策變量x(備用終端，鏈路或已有終端)和隨機路徑期t。

步驟2：

①如果x是備用終端且x的對應值等于t，則有：當在t周期備用終端沒有開放時，計算成本/容量的值，最低值的終端在t周期開放且x在整個規劃期間關閉。當在其他周期沒有終端被開放，則關閉x，且在t周期沒有終端被選擇打開；當在t周期備用終端開放時，則計算成本/容量的值，在整個規劃期內關閉最高值的終端，并且在t周期開放x；如果在t周期沒有新的終端開放，則在這個周期x將一直開放。

②如果x是現有的終端,則有：在t周期將x的容量模塊隨機更改為與其可用模塊不同的1個模塊；在t周期把x和隨機已有的終端y容量模塊進行交換。

③如果x是鐵路則與①同理。

步驟3：檢查新解是否在預算范圍內。如果不在，則舍棄并轉到步驟1。

2)當生成可行解，則在所有的路徑期內把貨流分配給整個網絡并計算此時的目標函數值C(γ)。C(γ0)為初始的目標函數值，如果C(γ)≤C(γ0)，則接受新解C(γ)。否則，是否接受這個非改進解由Boltzman函數e＾(-Δ/φ)決定，其中φ為當前溫度，Δ是C(γ0)和C(γ)之差。隨機產生1個?∈[0,1]，當?≤e＾(-Δ/φ)時，則接受這個非改進解；反之則不接受。如果C(γ)仍小于非改進解，則C(γ)為目前的最優值。

3)在每個溫度下產生并計算領域解的范圍K。對K進行計算后，其溫度隨φ(i+1)=Ω×φi函數的變化而減小,Ω是當溫度下降時的冷卻速率，且Ω∈[0,1]。設φ0為冷卻時的溫度，當φi≤φ0時，或者當設定的迭代次數中沒有最優解，則算法停止。

3 算例分析

圖1為隨機網絡,圖中的數字為對應編號。給出了12個城市、4個已有終端、2個備用終端、2個擴張期和7個路徑期。本算例采取2個擴張期，分別在第1年和第4年開始進行擴張決策，每個擴張期分別有3個場景，第1個擴張期的3種場景分別為:①隨機網絡有60%的概率不會發生中斷；②終端4有30%的概率發生中斷；③與城市12相連的所有鏈路出現中斷的概率為10%。第2個擴張期的3種場景分別為：①隨機網絡有75%的概率不會發生中斷；②終端6有20%的概率會發生中斷；③與城市3相連接的所有鏈路出現中斷的概率為5%。在擴張期內發生概率最高的第1個場景為隨機網絡中沒有發生中斷，即為正常情況，颶風和冰雪災害是第1個擴張期的另外2種場景；龍卷風和洪水是第2個擴張期的另外2種場景。每個中斷場景在其相應的擴張期開始時損壞程度最大，并且其嚴重程度隨著時間的推移而減少。本文算例在Python環境中進行求解。

3.1 多周期規劃方法對聯運網絡的影響

本文將單周期規劃方法與多周期動態規劃方法進行比較，并分析了2種方法對總運輸成本的影響。單周期規劃方法同時考慮了多周期中不同時期的所有OD對，并假設在所有情況和時間段內終端及鏈路中斷達到最大百分比，并通過計算得出最優方案，即在規劃期開始時開放備用終端5，擴容終端1和終端4并重鋪了終端4—終端3以及終端1—終端4的2條鐵路。與單周期相比，多周期危險品貨運網絡的最優方案為：在第1個擴張期擴容終端1，在第2個擴張期開放終端3以及擴容終端4，并且不進行鐵路重鋪。因此，與多周期規劃

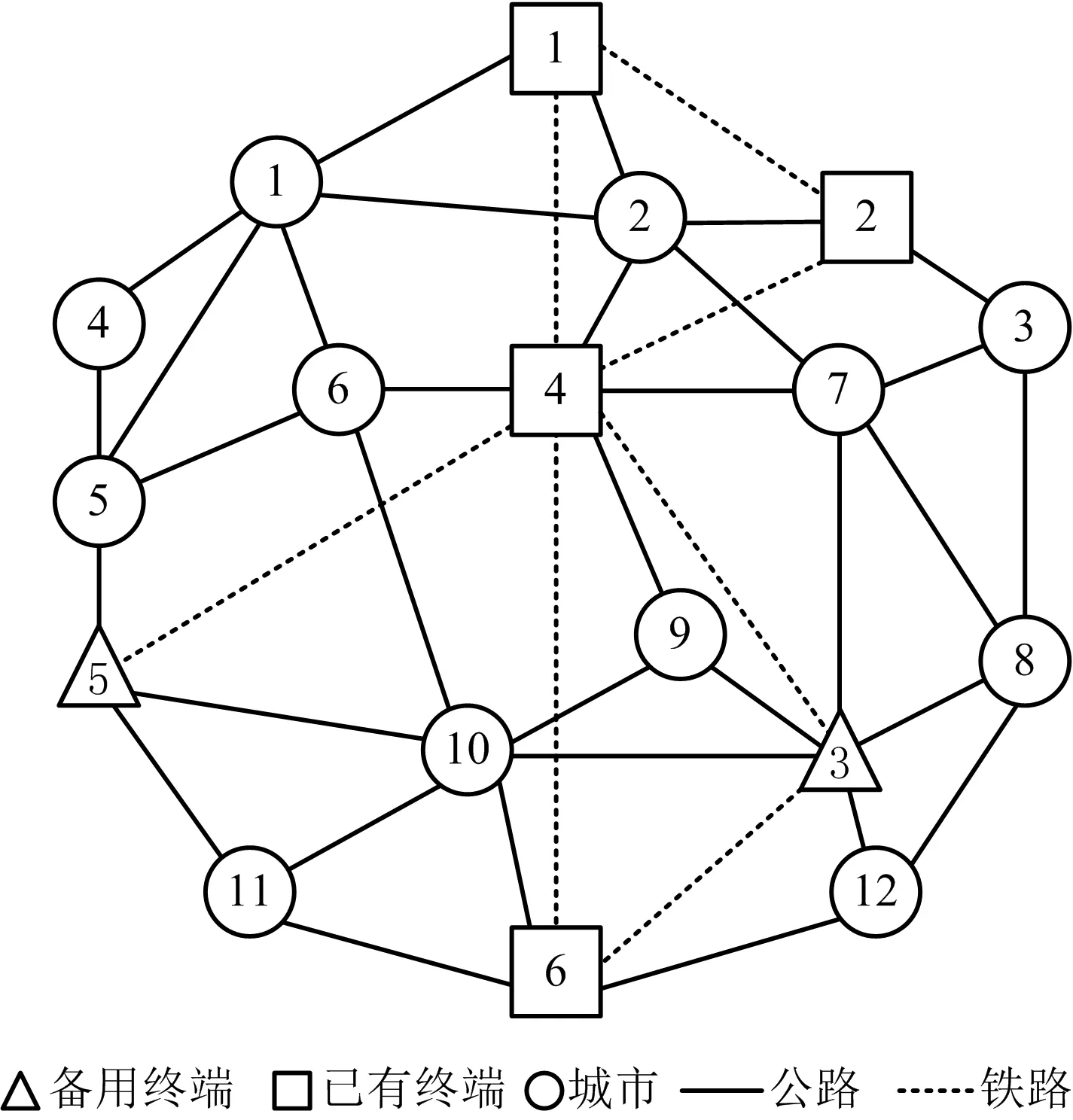
圖1 隨機網絡Fig.1 Random network

方法相比，單周期的總運輸成本在整個規劃期內約為1 312萬。而在相同的情況下，多周期在整個規劃期內總運輸成本約為726萬，總成本降低了55.3%。

由于多周期規劃是動態的，決策方案在不同的時間段內進行，且在所有路徑期內中斷的概率相對較小，而單周期規劃方法忽略了隨著時間的推移，危險品網絡終端從中斷到逐漸恢復這一過程和鏈路可能發生中斷的低概率情況，當終端重新獲得初始容量時，更多的貨物可以通過成本最低的路徑運輸，而這一過程只能在多周期的動態模型中考慮，所以在多周期規劃下沒有預算用在重鋪鐵路上。結果表明，大部分的預算用在了擴容已有的終端上，而不是開放新終端以及重鋪鐵路上，因此多周期的總運輸成本低于單周期的總運輸成本。表1為隨機網絡參數的取值，服從正態分布。

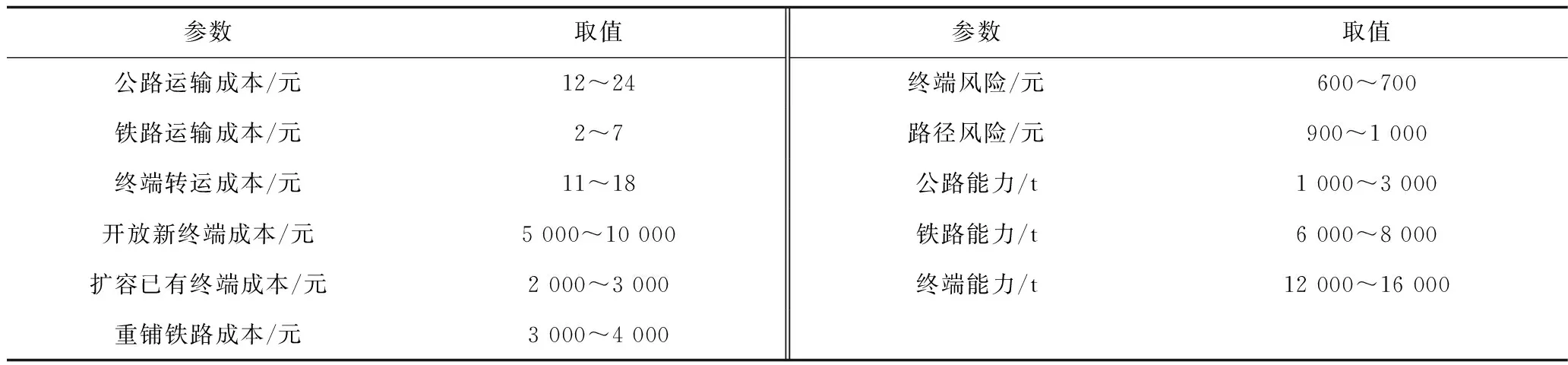
表1 隨機網絡參數Table 1 Random network parameter

3.2 多周期規劃方法對路徑決策的影響

在多周期動態模型求解出的最優方案基礎上，分析了第2個擴張期第2種場景下OD對(1～12)的路徑結果。圖2為第2個擴張期第2種場景下的路徑,圖中數字、圖形與圖1一致。如圖2所示，虛線鏈路為運輸成本和風險成本之和最小的路徑。由于受龍卷風的影響，終端6初期能力下降了80%，在第2個擴張期的第1年，即第1個路徑期，只有20%的終端容量可用于危險品運輸，因此，只有20%的危險品通過虛線鏈路進行運輸，其余80%的危險品則由其附近另一條成本較高的路線來運輸，即通過終端2所在的雙箭頭路線進行運輸；在擴張期的第2年，即第2個路徑期，終端能力逐漸恢復，其容量的60%可以進行危險品的運輸，因此，60%的危險品通過最短路徑進行危險品的運輸，其余40%的危險品由圖中雙箭頭路線進行運輸，同時擴容終端4以及開放終端3；在擴張期的第3年，即第3個路徑期，終端6的能力完全恢復，全部危險品由虛線路徑進行運輸，在第4個路徑期與第3個路徑期一致，具體情況如表2所示。

圖2 第2個擴張期第2種場景下的路徑Fig.2 The path under scenario 2 in the second expansion period

t路徑貨流/%1城市1—終端1—終端4—終端6—城市1230城市1—終端1—終端2—城市3—城市8—城市12702城市1—終端1—終端4—終端6—城市1260城市1—終端1—終端4—終端3—城市12403城市1—終端1—終端4—終端6—城市12100 4城市1—終端1—終端4—終端6—城市12100

此外，本文還分析了預算和轉運成本對總成本及路徑貨流的影響，如表3所示。一方面，預算對總成本及路徑貨流有較高的影響。當預算增加時，運輸路徑中的貨運流量將增加10%，同時總成本會降低；相反，當預算減少時，貨運流量會減少且總成本顯著增加。當減少預算時，開放終端的數量以及擴容終端的規模將變小，從而較經濟的路線運輸能力將減少，導致貨物只能通過其他高成本的路線運輸，進而增加了總運輸成本；同理，當預算增加時，在規劃期內可以開放和擴容更多的終端，增加經濟路線的運輸能力，降低成本。另一方面，轉運成本對總成本及路徑貨流的影響較低。當轉運成本增加時，總成本略有增加但是貨運流量保持不變；當轉運成本減少時，總成本略有降低并且貨運流量略有增加。由于終端上的轉運成本降低，總成本也隨之降低，路徑將變得更經濟，因此會有更多的危險品通過該路徑進行運輸；而轉運成本增加，會帶來總成本增加。

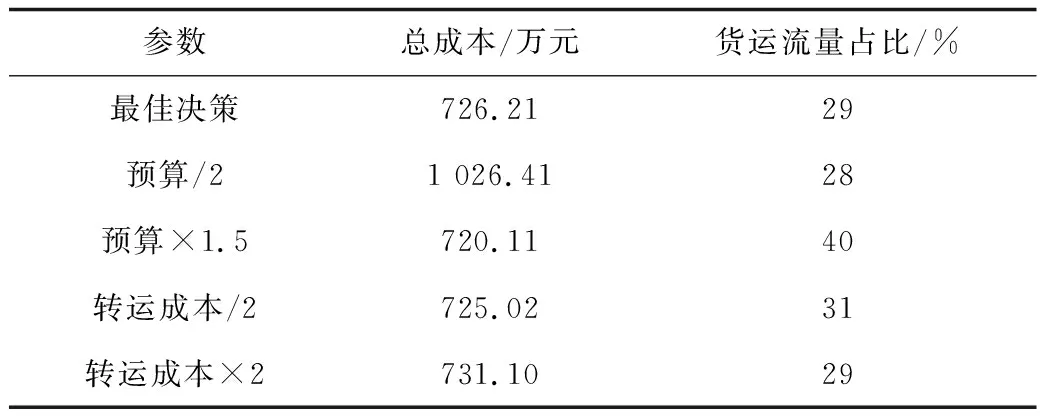
表3 靈敏度分析Table 3 Sensitivity analysis

4 結論

1)針對危險品多式聯運網絡擴張問題，考慮了成本及風險因素，并將風險進行量化處理以經濟損失的形式表現出來且賦以權重進行加和，最后，以總成本以及風險最低為目標，建立混合整數概率魯棒模型，在模型中將擴張決策和路徑決策的不同時間段相結合。

2)以小型隨機網絡為算例，利用模擬退火算法進行求解，解決了公鐵聯合貨運網絡擴張問題，得出危險品在不同時間段的運輸方案；通過對特定場景下其中1組OD對路徑進行分析，驗證了模型的合理性。

3)考慮建立時間窗下多周期的危險品聯合貨運實際網絡模型，以及研究不同權重對路徑的影響是未來研究的方向。