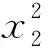深埋地下人員密集場所電梯與樓梯協同疏散的電梯運行參數研究

李田生，鄧建國，秦焰宏，駱 驪，牟玉斌，秦學思

(1.重慶城市綜合交通樞紐開發投資有限公司，重慶 400015； 2.西南交通大學地球科學與環境工程學院,四川 成都 611756)

隨著經濟社會的高速發展，城市核心區域各類深埋地下人員密集場所不斷涌現，如我國各大城市的地下城市綜合交通樞紐、地鐵換乘站和地下商場等。例如以重慶市沙坪壩綜合交通樞紐(以下簡稱“沙坪壩樞紐”)為例，其地下共有7層，地下埋深為36.5 m，高峰時段人員達14 238人，若不考慮人員上行疏散過程中疲勞度的影響，人員整體疏散時間超過0.6 h，若考慮人員疏散疲勞度的影響，人員整體疏散時間將超過1.2 h。深埋地下空間的特性使得火災條件下排煙排熱效果差、火災撲救難度大，故而傳統的樓梯疏散已經難以滿足人員整體安全疏散的需求，因此探索地下深埋人員密集場所電梯與樓梯協同疏散的可行性以及協同疏散的策略已成為國際上人員安全疏散領域的又一大熱點問題。

目前國外學者針對電梯疏散的研究工作取得了一些成果。在國外，20世紀中葉，一些學者就開始了超高層建筑利用電梯疏散問題的研究工作[1]；1974年，Bazjanac[2-3]提出了火災時考慮另一個安全出口疏散的思路，同時對緊急情況下電梯疏散的性能進行了分析；20世紀80年代，Klote[4-6]研究了電梯輔助老弱病殘等群體疏散的可行性，并總結出標準公式克服疏散時可能出現的活塞效應；20世紀90年代，Klote等[7-8]在研究利用電梯進行人員疏散可行性的基礎上，提出了電梯緊急疏散系統(EEES)的概念；20世紀90年代，ASME、NFPA、NIST舉行了一系列電梯疏散的學術會議[9]，在美國“9·11”事件之后，NIST于2008舉行了“Rethinking Egress”會議，探討了電梯疏散的優點；2015年，Shin[10]提出了用作自動噴水滅火系統和智能手機輔助疏散系統的電梯系統的撤離指導；2016年，Andree等[11]通過虛擬現實(VR)實驗，研究了出口選擇和高層建筑電梯疏散的等待時間。

在國內，許多學者圍繞電梯疏散的可行性也開展了大量研究。如胡傳平等[12]和宋文華等[13]針對高層建筑疏散的困境，采用數值模擬方法對比研究了采用樓梯和電梯進行疏散的有效性，并搜集現有成功采用電梯疏散的案例，進而闡明了樓梯與電梯協同疏散的可行性；陳輝等[14]針對高層建筑火災安全學的發展提出了“安全核”疏散體系的概念;張虎南[15]研究指出超高層建筑避難層應設置安全疏散電梯；胡傳平等[12]利用電梯疏散ELVAC模型，研究了電梯數量、人員分布等對電梯疏散的影響;朱惠軍[16]分析了采用高速穿梭電梯作為輔助疏散的新型疏散體系的可行性；李釗等[17]研究了Evacnet模型下的電梯疏散時間和電梯疏散效率的變化規律。

綜上可見，國內外學者圍繞電梯疏散進行了大量的研究，但是針對深埋地下人員密集場所電梯與樓梯協同疏散的研究還較缺乏。因此，為了探索城市核心區深埋地下人員密集場所電梯與樓梯協同疏散的可行性和最優的電梯運行參數，本文以重慶沙坪壩地下綜合交通樞紐為研究對象，利用Pathfinder疏散軟件建立了沙坪壩地下綜合交通樞紐人員疏散模型，研究了134種疏散場景下電梯運行參數對疏散時間的影響規律，并在此基礎上給出了該地下綜合交通樞紐電梯與樓梯協同疏散過程中電梯運行參數的最優建議取值，以為深埋地下人員密集場所電梯與樓梯協同疏散設計提供技術支撐。

1 疏散場景及模型參數設置

1. 1 疏散場景設置

重慶沙坪壩地下綜合交通樞紐工程總建筑面積約 75萬m2，其中地上約 51萬m2，地下約 24萬m2；地下7層布置有商業、公交車站、出租車站、換乘系統和地下停車場，地上布置了5棟超高層辦公寫字樓、1棟高層酒店、1棟高層辦公寫字樓。為了探索該深埋地下人員密集場所樓梯與電梯協同疏散過程中電梯運行參數對疏散時間的影響，考慮到模型中最不利情況下約有14 238人，為了方便模擬，忽略了負四層及以上樓層人員采用電梯疏散的方案，只考慮了3種人員疏散方案，方案一、方案二和方案三分別為：負七層的人員采用電梯疏散，負六層至負一層的人員采用樓梯疏散；負七層和負六層的人員采用電梯疏散，負五層至負一層的人員采用樓梯疏散；負七層至負五層的人員采用電梯疏散，負四層到負一層的人員采用樓梯疏散。取電梯運行參數為Pathfinder軟件默認值，模擬得到3種人員疏散方案下的疏散時間分別為2 293.4 s、2 098.3 s和2 892.6 s。由此可見，所選方案中采用方案二進行人員疏散時所用的疏散時間最少，故以該方案來模擬電梯與樓梯協同疏散可相對節省模擬所用的時間。在此基礎上，本次模擬設置的疏散場景如下：

(1) 疏散場景A：電梯加速度改變，不變的電梯運行參數為：電梯荷載取13人，電梯額定最大速度取5 m/s，電梯開關門時間取7 s，共有11種疏散場景，見表1。

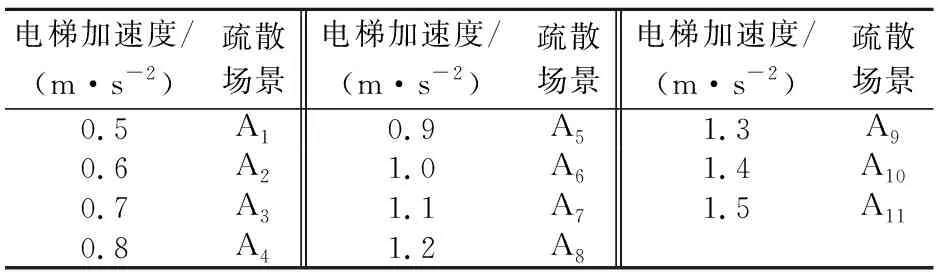
表1 疏散場景A：電梯加速度改變，其他電梯運行參數恒定

(2) 疏散場景B：電梯開關門時間改變，不變的電梯運行參數為：電梯荷載取13人，電梯額定最大速度取5 m/s，電梯加速度取1.2 m/s2，共有8種疏散場景，見表2。

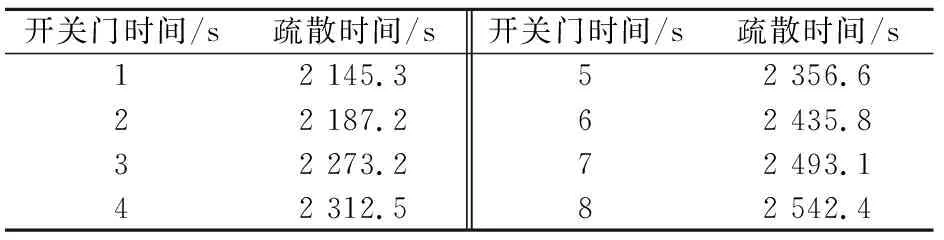
表2 疏散場景B：電梯開關門時間改變，其他電梯運行參數恒定

(3) 疏散場景C：電梯荷載和電梯額定最大速度改變，不變的電梯運行參數為：電梯開關門時間取7 s，電梯加速度取1.2 m/s2,共有35種疏散場景，見表3。

表3 疏散場景C：電梯荷載和電梯額定最大速度改變，其他電梯運行參數恒定

(4) 疏散場景D：電梯荷載和電梯加速度改變，不變的電梯運行參數為：電梯開關門時間取7 s，電梯額定最大速度取5 m/s,共有35種疏散場景，見表4。

表4 疏散場景D：電梯荷載和電梯加速度改變，其他電梯運行參數恒定

(5) 疏散場景E：電梯額定最大速度和電梯加速度改變，不變的電梯運行參數為：電梯開關門時間取7 s，電梯荷載取12人，共有25種疏散場景,見表5。

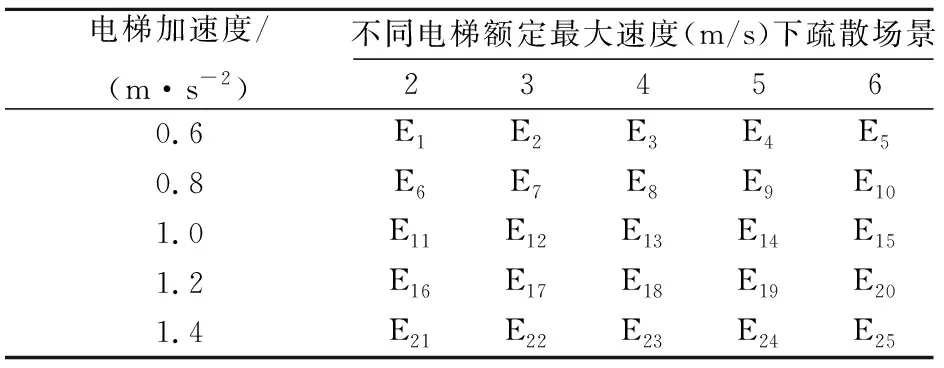
表5 疏散場景E：電梯額定最大速度和電梯加速度改變，其他電梯運行參數恒定

(6) 疏散場景F：電梯額定最大速度改變，不變的電梯運行參數為：電梯荷載取13人，電梯開關門時間取7 s，電梯加速度取1.2 m/s2，共有11種疏散場景，見表6。

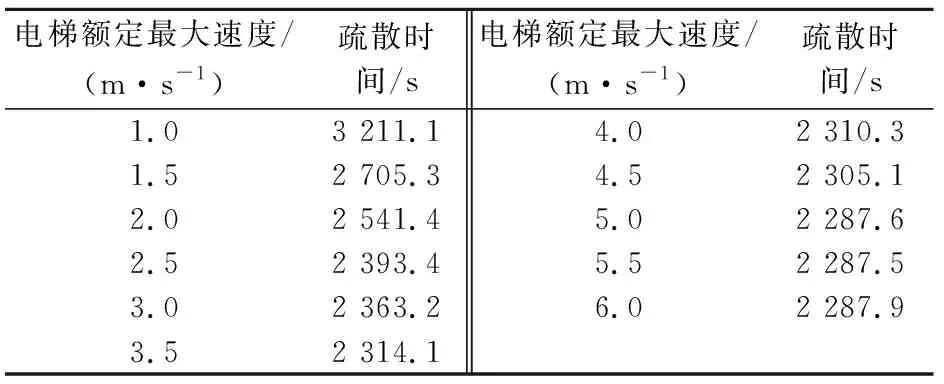
表6 疏散場景F：電梯額定最大速度改變，其他電梯運行參數恒定

(7) 疏散場景G：電梯荷載改變，不變的電梯運行參數為：電梯額定最大速度取5 m/s，電梯開關門時間取7 s，電梯加速度取1.2 m/s2，共有9種疏散場景，見表7。

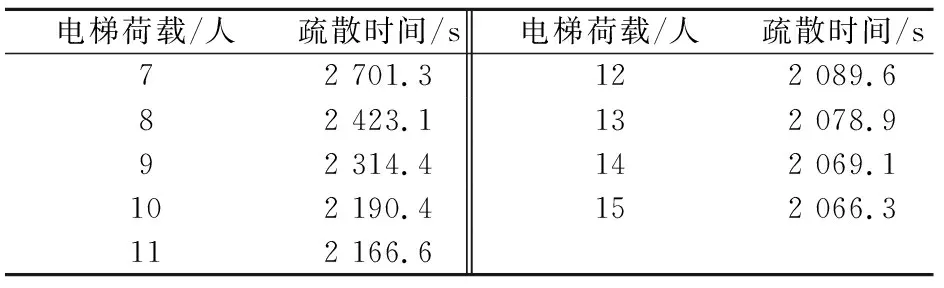
表7 疏散場景G：電梯荷載改變，其他電梯運行參數恒定

1. 2 人員參數設置

《重慶沙坪壩鐵路樞紐綜合改造工程性能化防火設計》報告中對高峰人流量進行了計算，計算公式為：人員數量=高峰每小時人數×超高峰系數×停留時間(min)÷60。根據該報告中的計算結果，在最不利情況下沙坪壩地下綜合交通樞紐的人數為14 238人，根據前述的負七層和負六層的人員采用電梯疏散，其余樓層的人員采用樓梯疏散的疏散方案(即方案二)，高峰時負七層和負六層各有3 659人和1 848人，故電梯承擔疏散人員的總負荷為5 507人。該建筑各場所具體疏散的人員數量見表8。

表8 建筑各場所疏散的人員數量(人)

沙坪壩地下綜合交通樞紐內的人員可分為成年男士、成年女士、兒童和老人4種類型，根據其使用功能，其人員類型組成可參照國際上通用的一般公共建筑場所推薦的數值比例設置。其中，站房候車區、站臺層以及出站區內人員類型的構成為：成年男士和成年女士各占40%，老人和兒童各占10%；各功能房間內人員類型的構成為：成年男士占60%，成年女士占40%。

根據Chen等[18]關于人員長距離上行疏散研究得出的結論：在擁擠條件下，人員在每個樓層的平均上行速度保持約為0.5±0.04 m/s的相對恒定值。因此，考慮疲勞度的條件下模型中所有人員的初始上行疏散速度均取0.5 m/s。

1. 3 電梯參數設置

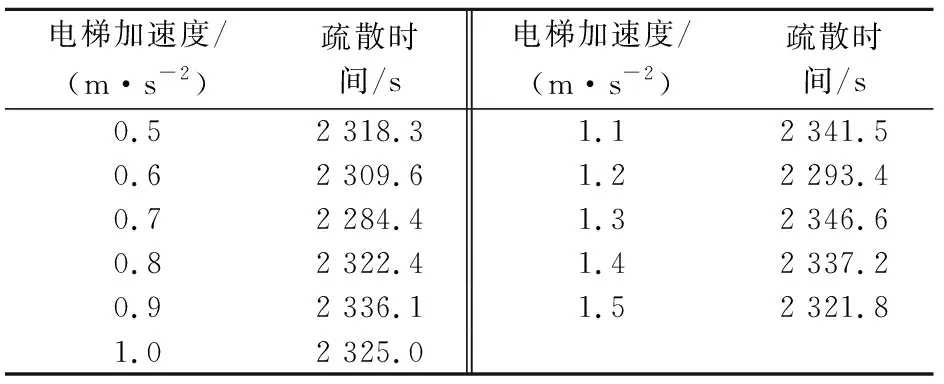
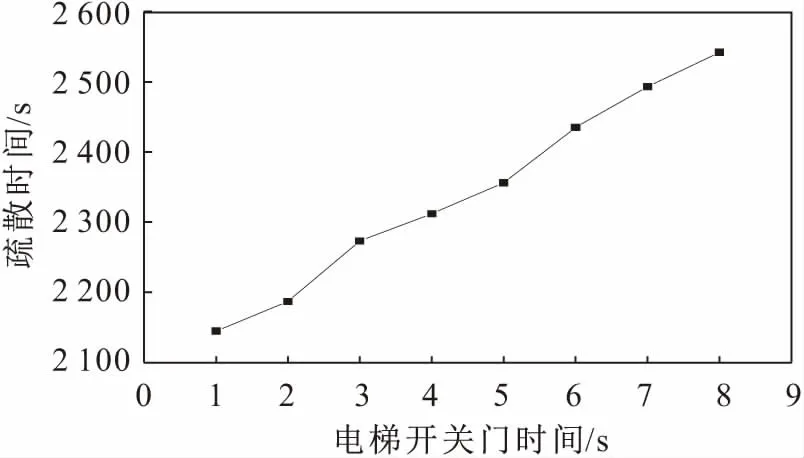
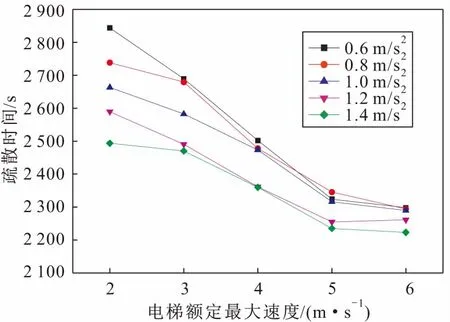
電梯運行參數的設定本文根據《電梯技術條件》(GB/T 10058—2009)[19]標準中的規定：當電梯額定最大速度為0 m/s

2 模擬結果與分析

2. 1 電梯運行參數對疏散時間的影響程度分析

為了得出電梯運行參數對疏散時間的影響程度，本文采用控制變量法，分別模擬得到不同疏散場景A、B、F和G下電梯加速度、電梯開關門時間、電梯額定最大速度和電梯荷載與疏散時間的關系，詳見表9至表12。

表9 電梯加速度與疏散時間的關系

表10 電梯開關門時間與疏散時間的關系

表11 電梯額定最大速度與疏散時間的關系

表12 電梯荷載與疏散時間的關系

根據表9至表12，利用SPSS軟件分別對這4個電梯運行參數與疏散時間進行了相關性分析，得到顯著性水平為0.01時的相關系數分別為0.001、0.997、-0.889和-0.775。由此可見，電梯荷載、電梯額定最大速度和電梯開關門時間與疏散時間的相關性較大，而電梯加速度與疏散時間的相關性很小，這可能是由于對于深埋地下僅有7層的沙坪壩地下綜合交通樞紐，不同電梯加速度下電梯疏散到地面所用的時間相差不大所致。因此，電梯運行參數對疏散時間的影響程度從大到小的排序為：電梯開關門時間>電梯額定最大速度>電梯荷載>電梯加速度。

2. 2 最優電梯運行參數分析

根據疏散場景B，本文模擬得到的電梯開關門時間與疏散時間的關系曲線，見圖1。

圖1 電梯開關門時間與疏散時間的關系曲線Fig.1 Relationship curve between door opening-and-closing time of elevator and evacuation time

由圖1可見，電梯開關門時間與疏散時間基本成正比關系，說明電梯的開關門時間越短，越有利于人員疏散。盡管電梯開關門時間越短電梯總的人員疏散時間也越少，但如果電梯開關門時間太短，候梯人員在進入電梯時可能會造成夾傷等事故，也會嚴重阻礙電梯的疏散效率，增加額外的電梯疏散時間。因此，電梯開關門時間要在保證人員能夠安全進出電梯的情況下盡可能地取最大值。根據《電梯技術條件》(GB/T 10058—2009)[19]標準中的規定，對于門的形式為中分自動門的電梯，開門寬度不大于800 mm時，電梯開關門時間應不大于3.2 s，結合沙坪壩地下綜合交通樞紐的實際情況，建議最優電梯開關門時間取為3 s。

在疏散場景C、D、E下，本次模擬得到的電梯運行參數與疏散時間的關系曲線，見圖2、圖3和圖4。

圖2 不同電梯荷載下電梯額定最大速度與疏散時間的關系曲線Fig.2 Relationship curve between elevator speeds and evacuation time under different elevator loads

圖3 不同電梯加速度下電梯額定最大速度與疏散時間的關系曲線Fig.3 Relationship curve between elevator speed and evac-uation time under different elevator accelerations

圖4 不同電梯加速度下電梯荷載與疏散時間的關系曲線Fig.4 Relationship curve between elevator load and evacuation time under different elevator accelerations

由圖2可見，在電梯荷載一定時，疏散時間隨著電梯額定最大速度的變化曲線先下降，直至電梯額定最大速度達到約5 m/s后，疏散時間趨于一個穩定值不再變化；當電梯荷載增加時，疏散時間隨著電梯額定最大速度的變化曲線分布較為稀疏，當電梯荷載達到約14人時，電梯荷載的變化對電梯額定最大速度與疏散時間關系的影響不大，該曲線整體的變化趨勢是電梯荷載越大，電梯額定最大速度越大，疏散時間會越短。

由圖3可見，當電梯加速度一定時，疏散時間隨著電梯額定最大速度的變化曲線先下降，直至電梯額定最大速度達到約5 m/s后，疏散時間趨于一個穩定值不再變化；當電梯額定最大速度在1～5 m/s之間時，不同電梯加速度下的疏散時間最多相差300 s；當電梯額定最大速度達到約5 m/s后，不同電梯加速度下疏散時間基本相同，疏散時間隨著電梯額定最大速度的變化曲線分布較為密集，該曲線整體的變化趨勢是電梯加速度越大，電梯額定最大速度也越大，疏散時間會越短。

由圖4可見，在電梯加速度改變時，疏散時間隨著電梯荷載的變化曲線先下降，直至電梯荷載達到約14人后，疏散時間趨于一個穩定值不再變化；在誤差允許的范圍內，不同電梯加速度下疏散時間隨著電梯荷載的變化曲線分布基本重合，這說明電梯加速度增大時，疏散時間隨著電梯荷載變化的規律是不變的，且疏散時間的大小只與電梯荷載有關。

對比圖2、圖3和圖4可見，電梯荷載和電梯額定最大速度對疏散時間的協同影響最大，電梯加速度和電梯額定最大速度對疏散時間的協同影響較小，電梯加速度和電梯荷載對疏散時間的協同影響最小。

綜上分析可見，對沙坪壩地下綜合交通樞紐人員疏散模型中的電梯運行參數，建議選取電梯荷載為14人、電梯額定最大速度為5 m/s、電梯加速度取軟件默認的值為1.2 m/s2、電梯開關門時間為3 s，此為最優電梯運行參數。

3 結 論

本文利用Pathfinder軟件建立了沙坪壩地下綜合交通樞紐電梯與樓梯協同疏散人員疏散模型，研究了不同疏散場景下電梯運行參數對疏散時間的影響規律，主要得出以下結論：

(1) 對于沙坪壩地下綜合交通樞紐人員疏散模型而言，電梯運行參數對疏散時間的影響程度從大到小的排序為：電梯開關門時間、電梯額定最大速度、電梯荷載和電梯加速度。其中，電梯加速度對疏散時間幾乎沒有影響；在保證人員能夠正常進出電梯的條件下，電梯開關門時間越短，疏散時間越少；電梯荷載越大，疏散時間越少；電梯額定最大速度越大，疏散時間越少。

(2) 根據電梯運行參數與疏散時間的關系曲線，可以得到疏散時間y與電梯開關門時間x1、電梯荷載x2和電梯額定最大速度x3的數學關系式如下:

y=57.607×x1+2 083.6

(3) 電梯荷載和電梯額定速度對疏散時間的協同影響最大；電梯加速度和電梯速度對疏散時間的協同影響較小；電梯加速度和電梯荷載對疏散時間的協同影響最小。因此，建議沙坪壩地下綜合交通樞紐中最優電梯運行參數的取值如下：電梯荷載為14人，電梯額定最大速度為5 m/s，電梯加速度為1.2 m/s2，電梯開關門時間為3 s。