無軸承磁通切換電機轉矩及懸浮力解析計算

鄭夢飛，周揚忠

(福州大學,福州 350108)

0 引 言

定子永磁磁通切換電機(以下簡稱FSPMM)相較于傳統永磁體轉子的永磁同步電機而言，由于永磁體放置于定子側，轉子由硅鋼片簡單疊壓而成，具有結構簡單可靠，散熱容易，轉矩密度高等優點[1-4]。因此，將無軸承技術應用到傳統FSPMM中，即無軸承磁通切換電機(以下簡稱BFSPMM), 在保有無軸承技術所帶來的無需機械軸承，無需潤滑，定轉子之間完全隔離等優點前提下[5-6]，克服了傳統無軸承永磁電機在一些應用場合下轉子為一次性使用費用高及永磁體高溫退磁等缺陷[7-8]，在生物醫藥、半導體及化學化工領域具有廣闊的應用前景。

回顧傳統FSPMM的一般分析方法，對于BFSPMM的研究可借助于FSPMM相關理論分析方法。然而，由于在FSPMM中永磁體位于定子側，且定轉子均為凸極結構，傳統成熟的永磁同步電機理論無法直接應用。目前，學術界對于雙凸極氣隙研究方法主要分為有限元分析法[9]、等效磁網絡分析法[10]、基于磁動勢-磁導分析法[11]、子域法[12]、空間離散法[13]、許-克變換[14-15]、傅里葉分析法[16]等方法。其中，有限元與等效磁網絡分析方法應用最為廣泛，但存在模型構造復雜且計算時間長等問題；子域法和基于磁動勢-磁導分析法及傅里葉分析法雖然均能得到雙凸極氣隙磁密的解析表達式，但由于涉及到大量的解方程等復雜代數運算，實際應用不多。相較而言，許-克變換計算簡單、模型構造方便且物理概念更加清晰，已逐漸成為雙凸極氣隙主流分析方法之一。

目前，無軸承技術已經成功應用到幾乎所有的電機，相關理論分析及數學模型構建已經十分成熟。然而，綜合已發表的BFSPMM相關文獻，BFSPMM相關理論分析、懸浮力與電磁轉矩模型構建大部分仍然是借助于有限元分析[17-19]與等效磁網絡[20]，因此，存在計算時間長且模型構造復雜等缺陷。同樣，由于無法得到氣隙磁密解析表達式，其對于電機結構參數十分敏感，電機結構的細微更改均將帶來大量的模型重建工作及計算時間，所得到的相關數學模型不具有實際通用性。

基于此，本文借助傳統FSPMM中基于許-克變換的雙凸極氣隙分析方法，推導出電機關鍵電磁參數的解析表達式，并基于磁齒輪效應與麥克斯韋張量法分別構建BFSPMM中轉矩及懸浮力的數學模型。最后，利用有限元仿真結果驗證了所推導的解析模型的正確性。

1 六相單繞組BFSPMM拓撲結構及懸浮力生成原理

1.1 拓撲結構

本文所研究的BFSPMM為12/10結構，單繞組連接方式，其拓撲結構如圖1所示。電機定子由12塊U形鐵心構成，且相鄰兩個U形鐵心夾著沿切向交替充磁的永磁體，而轉子由硅鋼片簡單疊壓而成，有10個齒。電機六相繞組電流iA～iF同時含有控制轉子切向旋轉的電流iAT～iFT和控制轉子徑向懸浮的懸浮電流iAS～iFS。定義三相懸浮電流iAD、iBE與iCF，懸浮電流iAS～iFS滿足iAS=iDS=iAD，iBS=iES=iBE，iCS=iFS=iCF。

T6恒功率變換矩陣如下：

(1)

可將六相繞組相電流分解到控制轉矩輸出的轉矩平面電流iαTiβT，控制懸浮力輸出的懸浮力平面電流iαSiβS與零序平面電流io1io2：

因此，由式(2)可知，按照如圖1所示的繞組連接方式，電機六相繞組轉矩生成部分可以等效為六相對稱繞組A～F通入的轉矩電流iAT～iFT；而懸浮力生成部分可以等效為三相懸浮繞組AD，BE與CF相(由A相與D相，B相與E相，C相與F相分別構成)通入對稱的懸浮電流iAD，iBE與iCF得到。

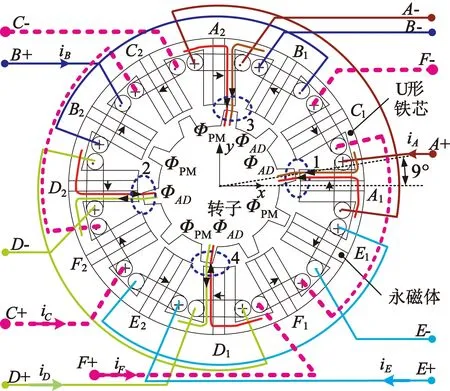
圖1 BFSPMM橫截面圖

1.2 懸浮力生成原理

以AD相繞組為例，在圖1的轉子位置角處，4個氣隙定轉子重疊面積相等，且電機氣隙圓周關于電機中心點處處對稱，故由iAD在4個氣隙處生成的磁通均相等，令其為ΦAD。相對于永磁磁通ΦPM，其中氣隙1與氣隙3總磁通增大為ΦPM+ΦAD，而氣隙2與氣隙4總磁通減小為ΦPM-ΦAD。故由麥克斯韋張量法可知，此時電機將受到在空間上近似為45°圓周角方向的磁拉力。同理分析由BE，CF相懸浮電流電流iBE，iCF生成的磁拉力，用矢量圖表示如圖2所示。由圖2可知，三相懸浮電流生成的懸浮力空間對稱，因此通過通入合適的懸浮電流即可產生沿空間對應方向及大小的懸浮力。

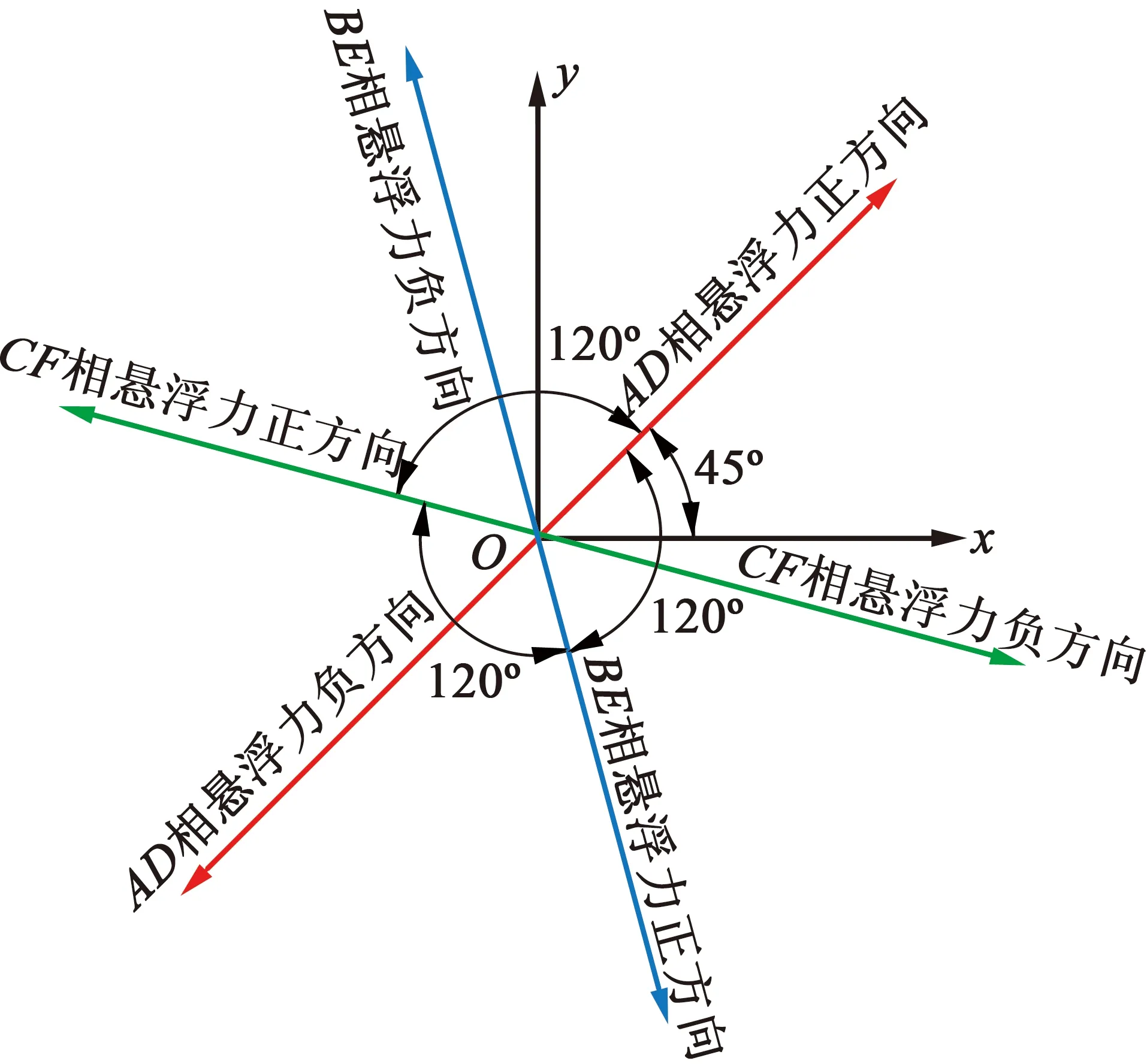
圖2 AD，BE和CF相產生的懸浮力空間矢量圖

2 氣隙磁密分布

2.1 氣隙磁導分布

為使許-克變換應用于BFSPMM中，本文設定以下前提條件:電機定轉子鐵心相對磁導率為無窮大;定轉子槽為無窮深結構；鐵心上相鄰的兩個槽之間不存在耦合；電機氣隙磁密分布沿徑向保持不變。

對于定子永磁型的BFSPMM而言，由于定子鐵心不完整，氣隙不為閉合區域，無法直接應用許-克變換將雙凸極氣隙映射至隱極氣隙。若采用導磁橋形式將定子鐵心構成整體，由于導齒橋飽和，不滿足鐵心相對磁導率為無窮大的前提條件。然而，即使定子鐵心為整體且不飽和，由于雙凸極結構，氣隙閉合區域頂點數超過4個，將難以得到許-克變換解析表達式，需要借助相關數值算法逼近，將耗費大量的計算時間。

另一方面，雙凸極氣隙磁導可以表示[21]：

式中：θ為電機氣隙圓周角；θr為電機轉子位置角;Λs(θ)為僅有定子凸極時氣隙磁導分布；Λr(θ,θr)為僅有轉子凸極時氣隙磁導分布;Rsi與Rro分別為電機定子內徑與轉子外徑；μ0為真空磁導率。

因此，對于BFSPMM而言，分別計算僅考慮定子凸極效應與轉子凸極效應下的氣隙磁導分布，由式(3)就可以計算得到電機氣隙磁導分布。

以電機定子凸極而轉子為光滑圓柱體為例，在z平面，電機定子單個槽模型如圖3(a)所示。為簡化模型，利用式(4)將其映射至w平面時保持w1w2平行于w1w5，滿足鐵心槽無限深的前提條件。如圖3(b)所示，g可由式(5)計算得到。

(4)

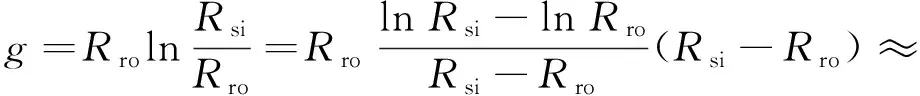
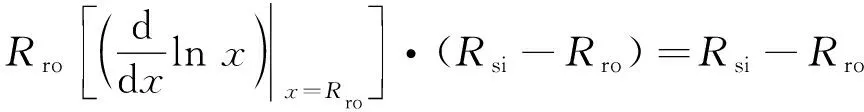
為將點t1-t5映射至點w1-w5，t平面的上半平面映射至w平面的氣隙區域，如圖3(c)所示，利用式(6)的許-克變換公式：

式中：

(7)

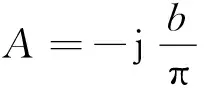
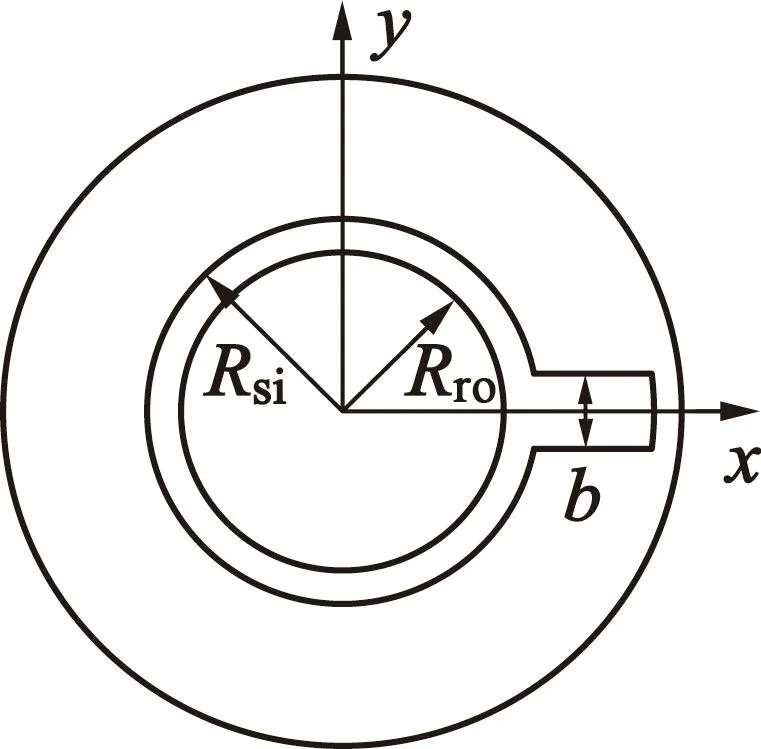
(a) z平面

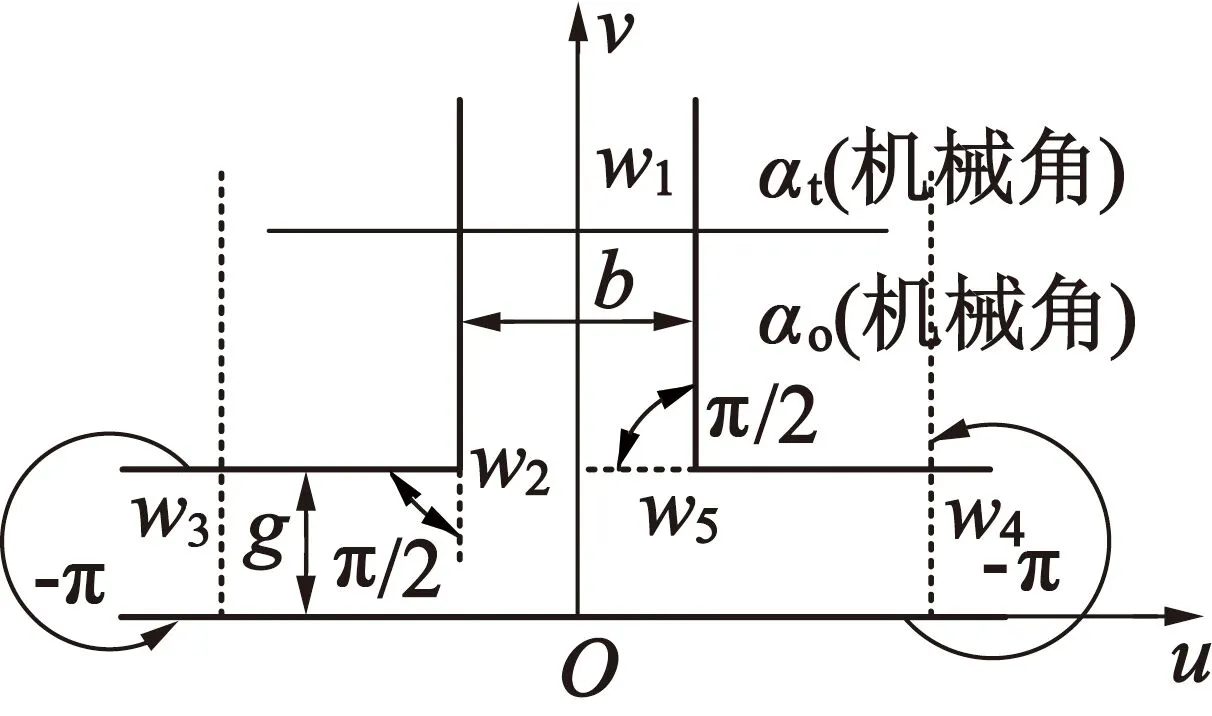
(b) w平面

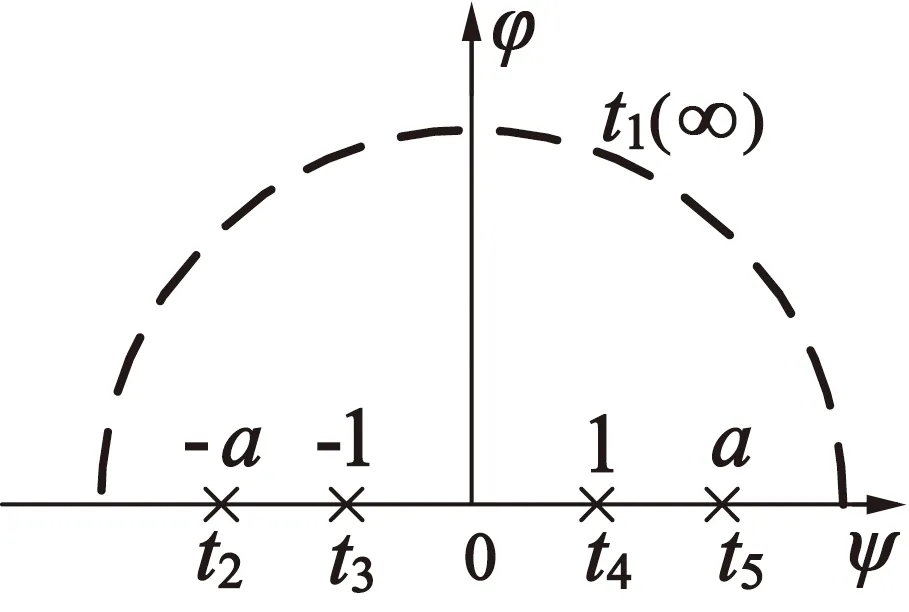
(c) t平面

在t平面中的上半平面，若滿足正負實軸上磁勢均恒定，且二者相差fm的狄利克雷邊界第一邊界條件，則其磁動勢分布：

(9)

圖3(b)中狄利克雷第一邊界條件：定子齒表面磁動勢為fm，而光滑轉子表面磁動勢為0，對應t平面中t1t2t3與t4t5t1表面磁動勢為fm，而t3t4表面磁動勢為0，即沿正實軸方向在t=-1處磁勢減小fm，而在t=1處增大fm。因此，由式(9)可知，圖3(c)中t平面磁動勢分布：

(10)

t平面磁密Bt：

(11)

因此，z平面磁密：

(12)

考慮到前文所述的前提條件，將式(12)簡化：

(13)

式(13)中存在t平面變量，為得到z平面的磁導表達式，需要求解式(6)的反函數。然而，該反函數難以推導得到，因此，無法直接得到氣隙磁密的解析表達式。由于單個槽下單凸極氣隙磁導分布可以表示[21]：

(14)

式中：α0與αt分別表示槽寬及齒距機械角，如圖3(b)所示，β按照如下定義：

(15)

因此，借助式(1)，僅需計算氣隙最大磁密Bzmax與最小氣隙磁密Bzmin，即可得到氣隙磁密分布。

氣隙最大磁密Bzmax在t=±1處取得:

(16)

氣隙最小磁密Bzmin在t=0處取得：

(17)

故：

(18)

本文電機為12/10結構，將永磁體等效為氣隙，電機定子U形鐵心有24個齒，轉子有10個齒。因此，由式(14)可知，僅考慮定子凸極效應時氣隙磁密分布傅里葉級數展開：

(19)

式中：bs與τs分別為定子槽寬與齒距，βs為式(18)在定子側的取值。

同理，僅考慮轉子凸極效應時氣隙磁導分布的傅里葉級數展開(任意一個轉子槽中心線與z平面正實軸重合時即為轉子初始位置)：

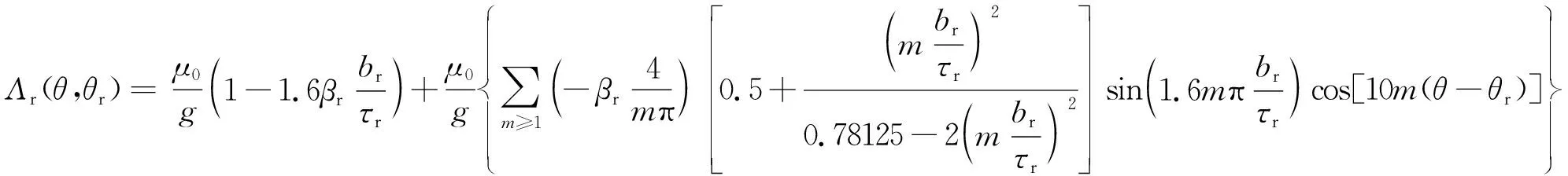
式中：br與τr分別為轉子槽寬與齒距，βr為式(18)在轉子側的取值。

由式(1),式(19)和式(20)即可計算雙凸極氣隙磁導分布Λrs(θ,θr)。

2.2 永磁氣隙磁密

當定子齒不飽和時，相鄰兩個永磁體所夾的U形齒極靴上的磁動勢相等且保持為恒值。因此，若利用Cater系數對定轉子槽的齒槽效應進行補償，可直接將BFSPMM雙凸極氣隙等效為隱極氣隙求解氣隙永磁磁勢分布，如圖4(a)所示。圖4中定轉子Carter系數分別表示為kcs與kcr，其分別可由式(21)和式(22)計算得到：

(21)

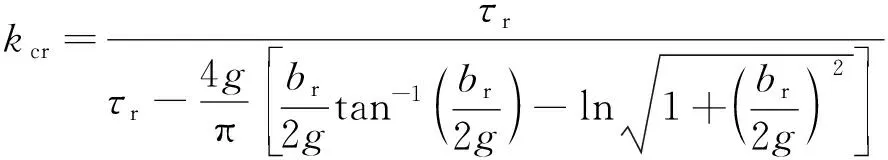
氣隙沿圓周角θ分布的永磁磁動勢Fpm如圖4(b)所示，結合圖4(a)可以計算得到Fm：

(23)

式中:Hc表示永磁體矯頑力；Rpm表示永磁體磁阻，其與R1與R2可由下式計算得到：

(24)

式中：τt表示相鄰兩個永磁體所夾U形鐵心在氣隙側的切向長度，本文中τt=π/8。

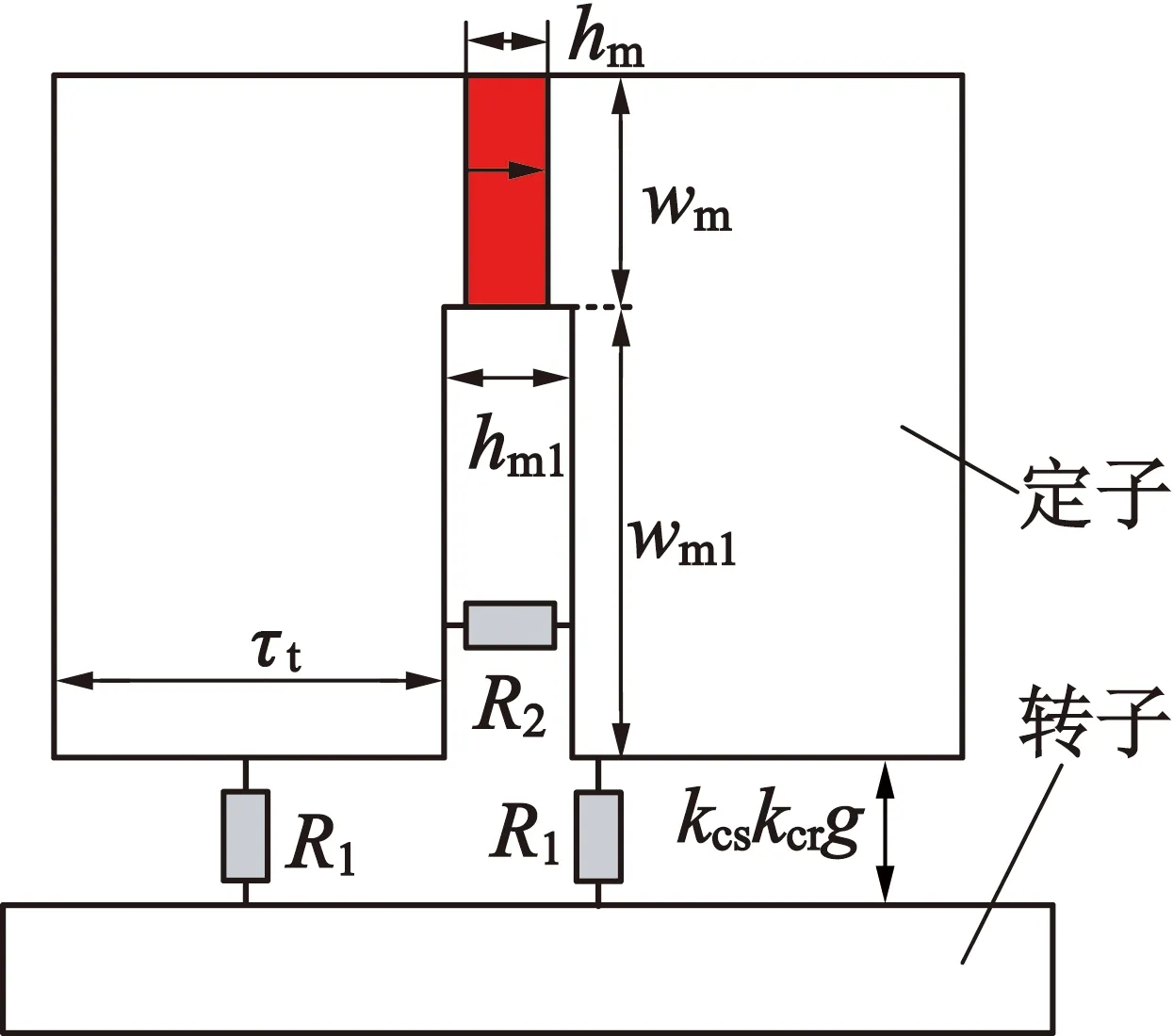
(a) 等效磁路

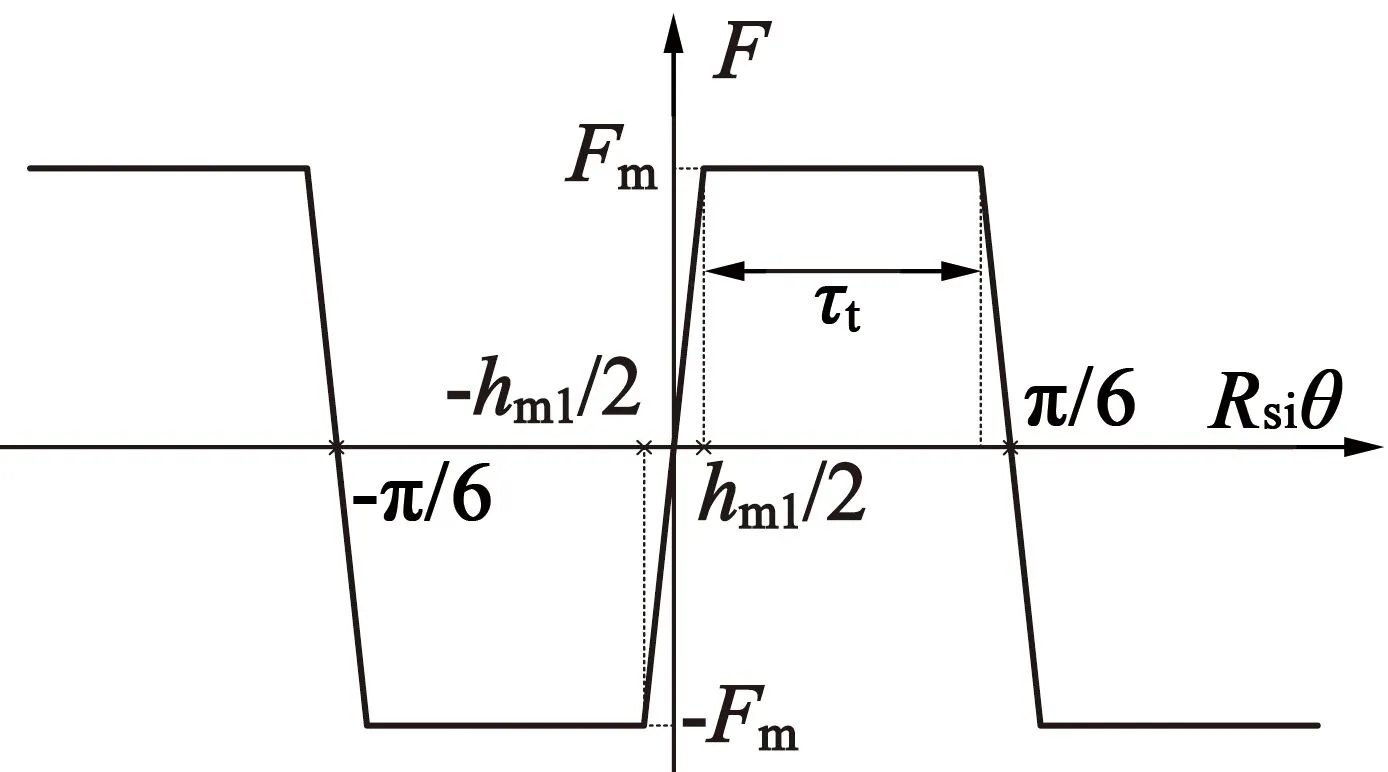
(b) 磁動勢分布

因此，由圖4(b)可知，永磁磁動勢可用傅里葉級數展開：

sin[6(2n-1)θ] (25)

聯立式(1)，永磁氣隙磁密分布可以表示：

Bpm(θ,θr)=Fpm(θ)Λrs(θ,θr) (26)

2.3 A相繞組電流氣隙磁密

如圖5(a)所示，用Carte系數對轉子槽的齒槽效應進行補償，將轉子等效為圓柱體。以A1齒為例，類似于Fpm的推導過程，可以推導得到圖5(b)中3個磁勢幅值FAD1，FAD2及FAD3的值：

(27)

式中：Nc為電機相繞組匝數；R3與R4：

(28)

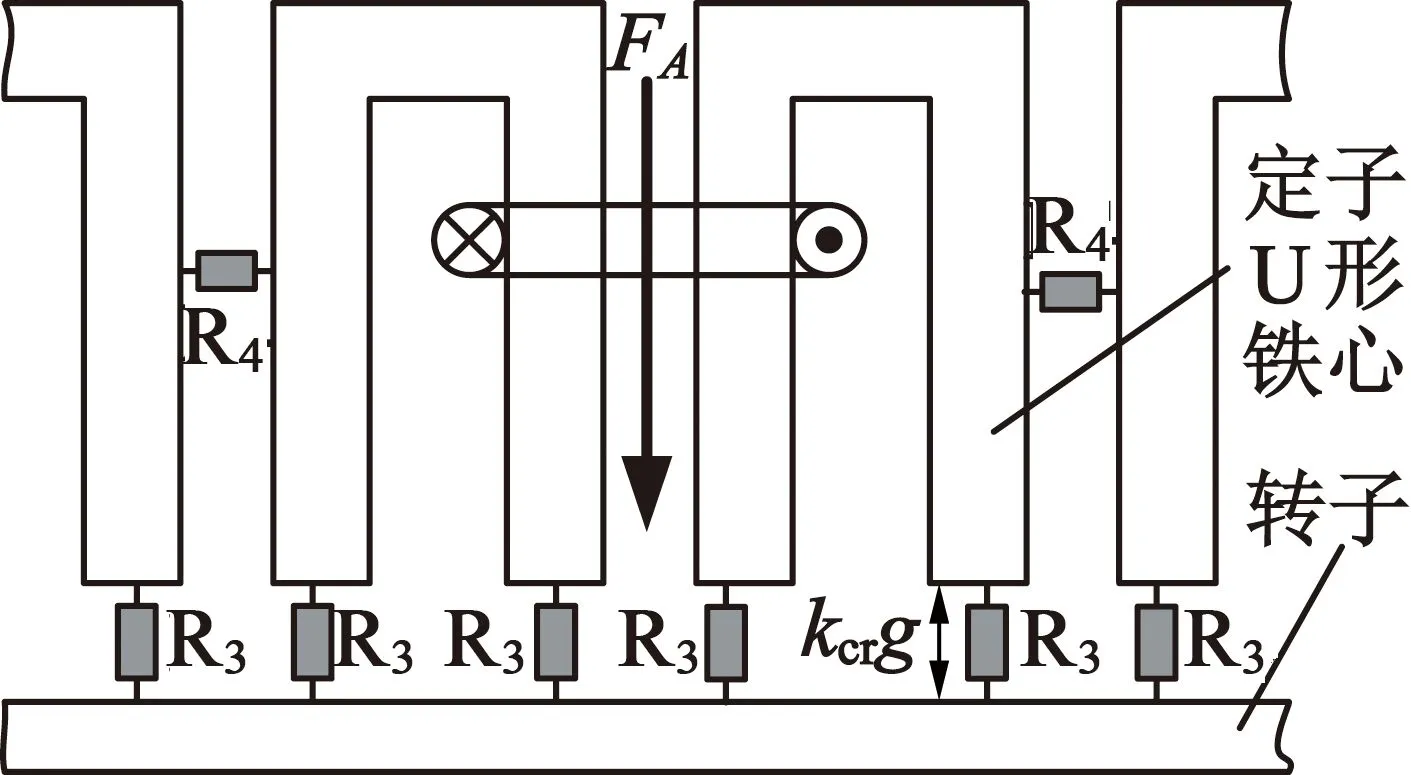
(a) 等效磁路

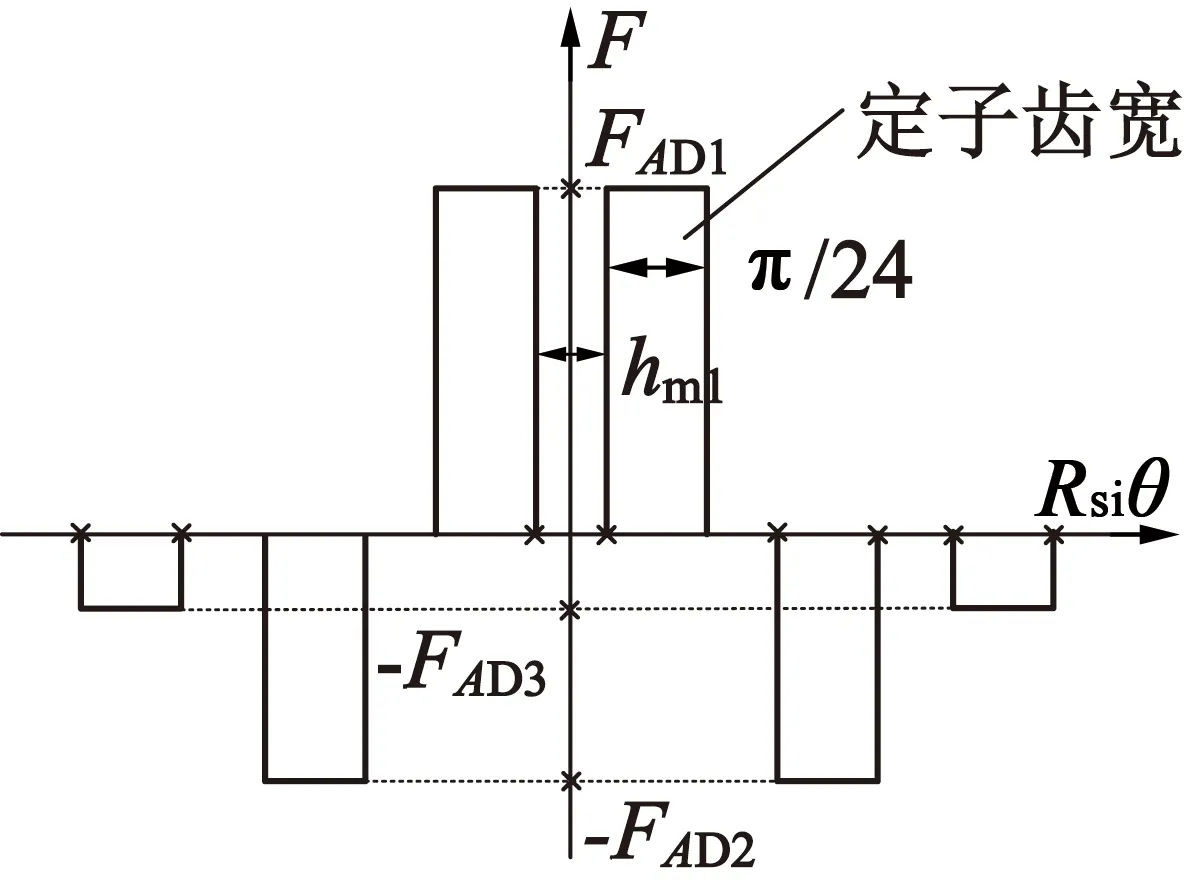
(b) 磁動勢分布

考慮到A2齒沿圓周超前A1齒90°圓周角，因此由A相繞組電流iAD產生的磁動勢的傅里葉級數展開可以表示：

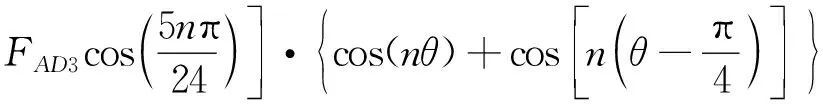
聯立式(1)，A相繞組電流iAD產生的氣隙磁密分布可以表示：

BA(θ,θr)=FA(θ)Λrs(θ,θr) (30)

3 懸浮力與轉矩數學模型

3.1 轉矩數學模型

在無偏心情況下，由于懸浮電流產生的沿轉子表面切向的洛倫茲力合力為0，因此BFSPMM轉矩生成部分可以等效為傳統FSPMM。但不同于傳統永磁同步電機，FSPMM由于永磁體位于定子側，定子電樞電流與永磁體產生的磁動勢經轉子調制在氣隙中產生多種極對數的諧波，其中參與轉矩輸出的磁密極對數遠不止一個。

為分析方便，定義pr為轉子極對數，ps為定子永磁體極對數，Ωr為電機轉子旋轉機械角速度，對于本文所述的12/10 BFSPMM，pr=10，ps=6。

由電機定子側永磁體生成的永磁磁勢經過轉子齒調制，在氣隙中產生極對數為4，16，8，28(|kpr±(2i-1)ps|,k=1,i=1,2，…)的永磁磁密，在空間上均旋轉同步于prΩr，因而繞組中感應出電角頻率為prΩr的基波反電動勢；由電角頻率為prΩr的對稱電樞電流產生的磁動勢經過轉子齒調制，在氣隙中產生極對數為4，8，16，20(4q,q=3r-1或q=3r-2,r=1,2,…)的電樞電流磁密。二者在空間上旋轉均同步于prΩr，如表1所示。表1中，負號表示旋轉方向同轉子旋轉正方向相反。

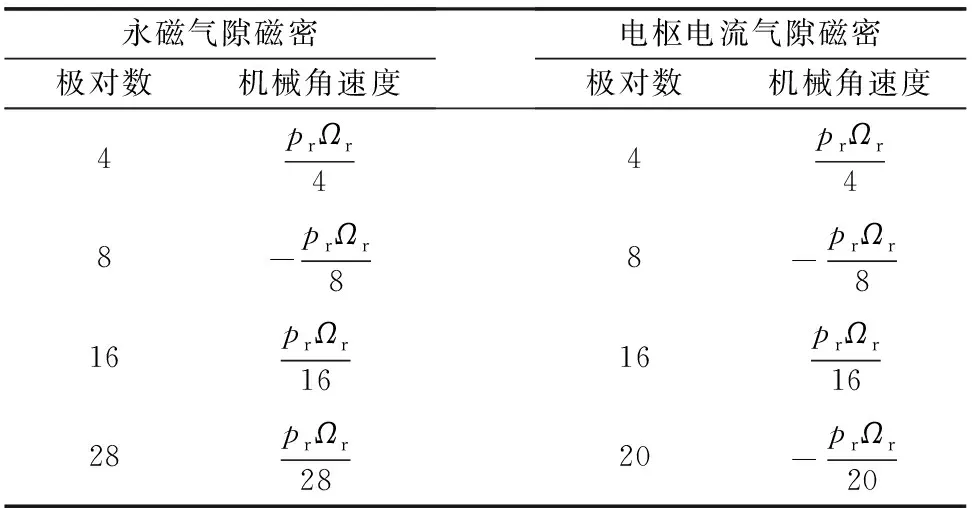
表1 氣隙磁密極對數及其對應的旋轉速度

由此可知，由電機繞組中對稱電流在氣隙中產生的旋轉諧波磁密，其極對數正比于4，且同步于靜止的永磁磁動勢經轉子基波磁導調制之后，極對數正比于pr-ps的旋轉的永磁諧波磁密，該現象即體現為磁齒輪效應，即繞組極對數pw滿足：

pr=ps+pw(31)

因此，可將FSPMM的功率部分等效為無窮多個極對數為4q(q=3r-1或q=3r-2,r=1,2,…)，但相繞組反電動勢頻率均為prΩr/(2π)的永磁同步電機疊加，直接推導得到電機電磁轉矩：

式中：ea～ef為相繞組反電動勢；Irms為相繞組電流有效值；ψf為相繞組匝鏈的永磁磁鏈；φe為相繞組電流同反電動勢相位差。

以A相繞組為例，借助式(26)，ψf可以通過下式計算得到：

(33)

式中：Lstk為電機實際軸長。聯立式(32)與式(26)即可得到電機電磁轉矩解析表達式。

3.2 懸浮力數學模型

借助麥克斯韋張量法，電機轉子軸向單位長度受到的徑向電磁力Fsus可以表示：

(34)

本文取Γ1為在氣隙中半徑為Rh=(Rsi+Rro)/2的閉合圓周。在BFSPMM中一般氣隙徑向磁密Bn遠大于切向磁密Bt。因此，考慮電機實際軸長Lstk，電機轉子在x，y方向受到的電磁力可以分別表示：

(35)

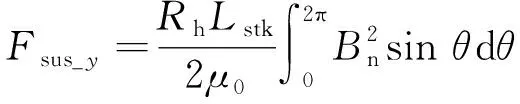
以AD相為例，由圖1可知，AD相通入電流iAD產生的氣隙磁密沿電機中心徑向對稱的兩側分別為ΔBn與-ΔBn，且Bn也沿電機中心徑向對稱，因此產生的x方向懸浮力可表示：

同理，y方向懸浮力：

(38)

式中：Bn與ΔBn可分別由式(26)與式(30)計算得到。至此，本文完成了電機懸浮力及轉矩的解析數學模型構建。

4 有限元仿真驗證

為驗證本文所推導的12/10 BFSPMM解析數學模型的正確性，按照表2構建BFSPMM有限元仿真模型。

首先按照式(33)計算A相繞組永磁磁鏈，每項傅里葉級數展開均取100項，其與有限元分析對比結果如圖6所示。由圖6可知，二者正弦度高，且相位基本一致，僅有幅值上不到6%的細小偏差，這主要是由于在永磁磁動勢幅值計算過程中忽略了氣隙磁密沿徑向分布的細微差異及相鄰兩個槽之間的輕微耦合，在實際應用過程中可將二者影響忽略。

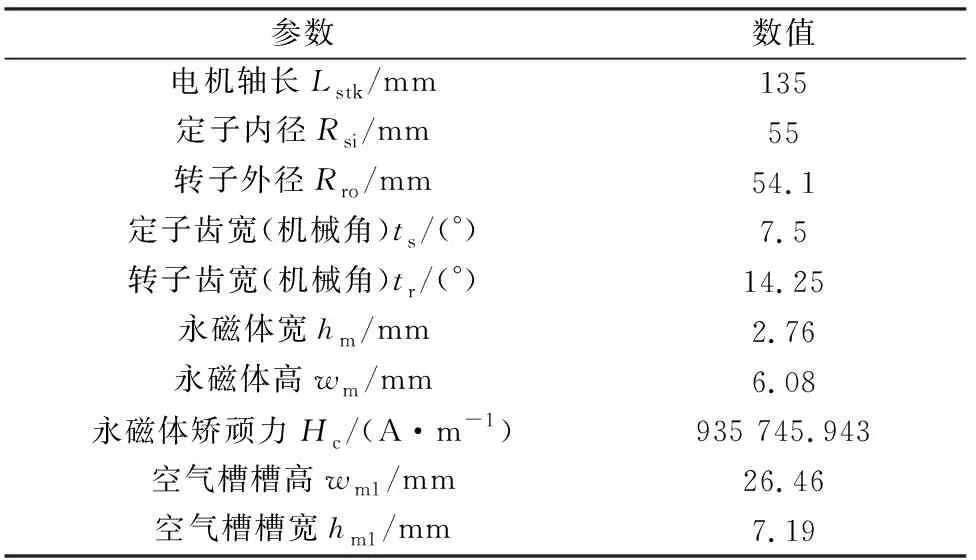
表2 電機結構參數

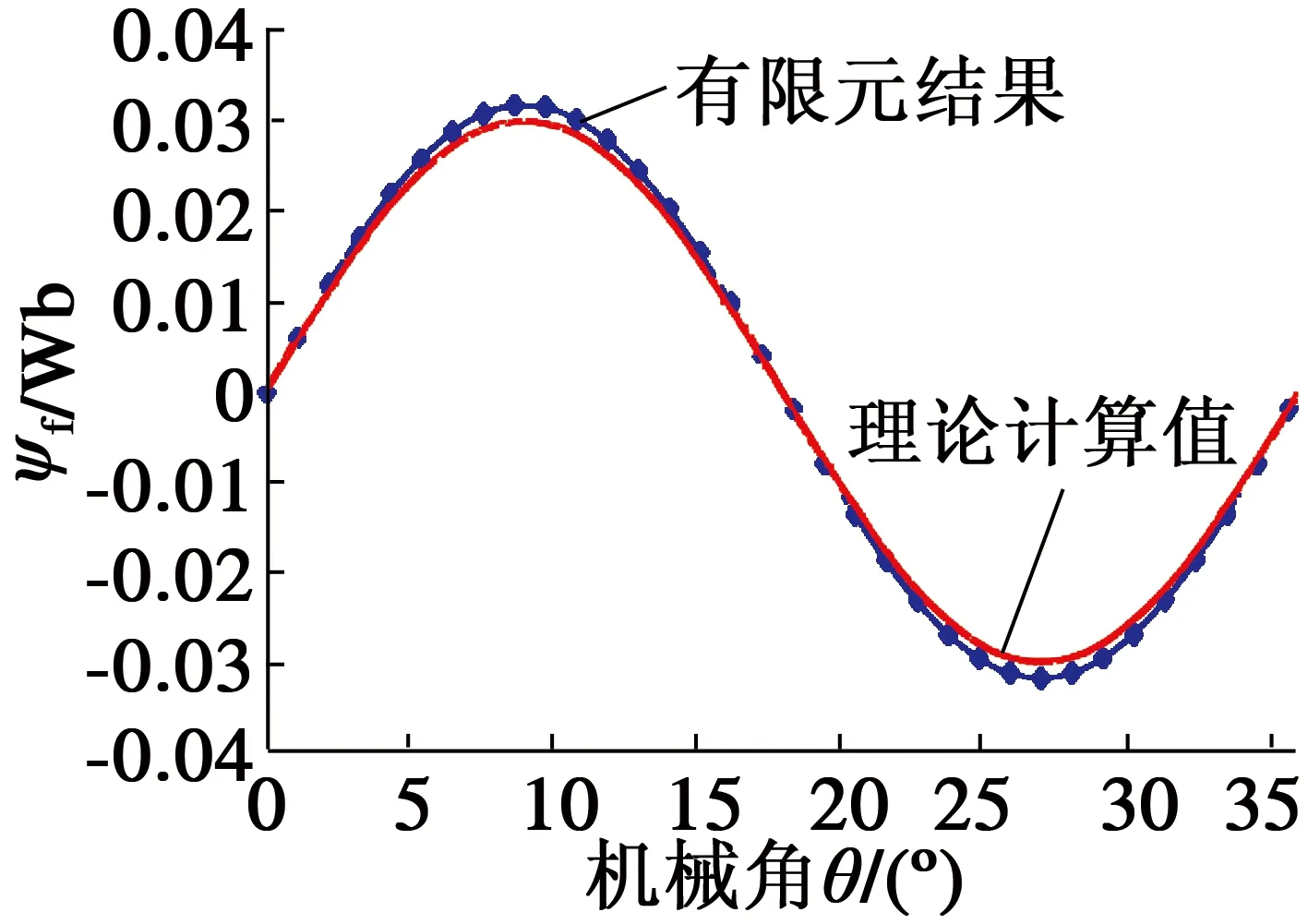
圖6 A相繞組永磁磁鏈

圖7表示電機AD相繞組通入單位正向懸浮電流時，由式(37)與式(38)計算得到的懸浮力與有限元分析之間的對比(傅里葉級數展開均取100項)。

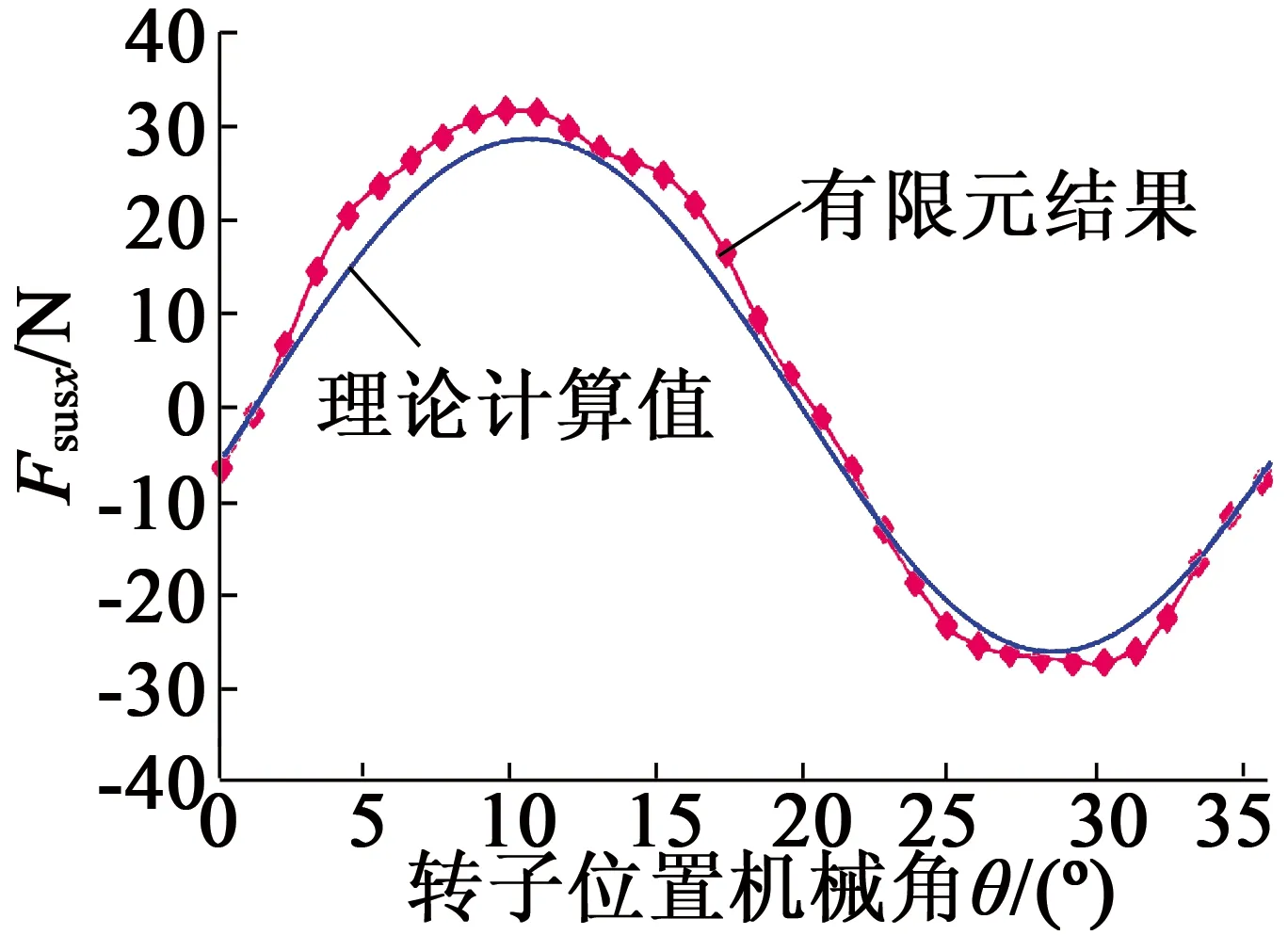
(a) x方向

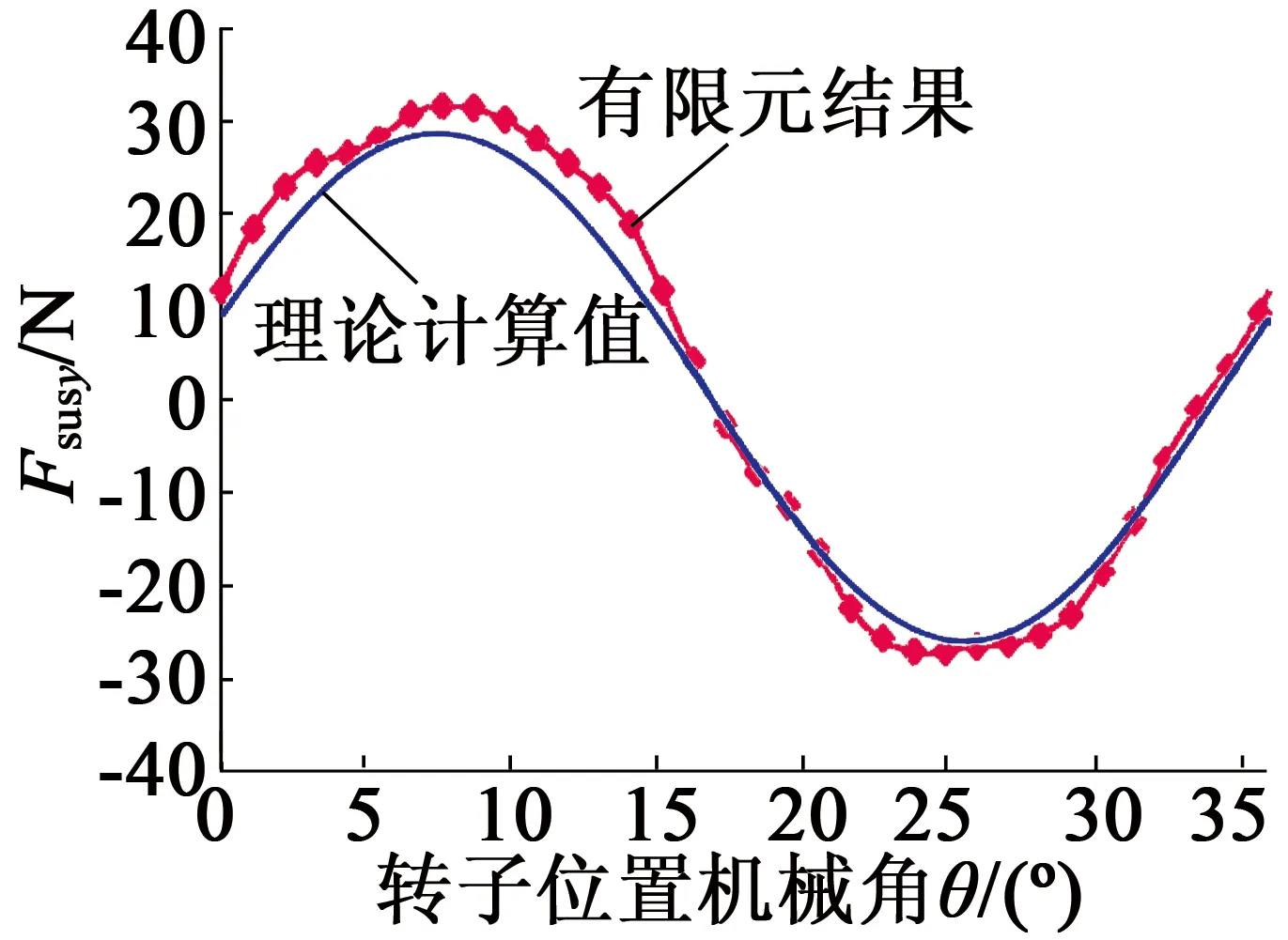
(b) y方向

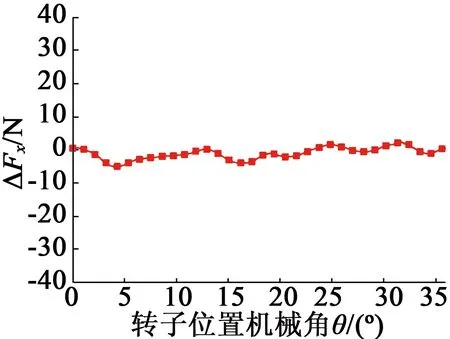
(c) x方向懸浮力計算誤差

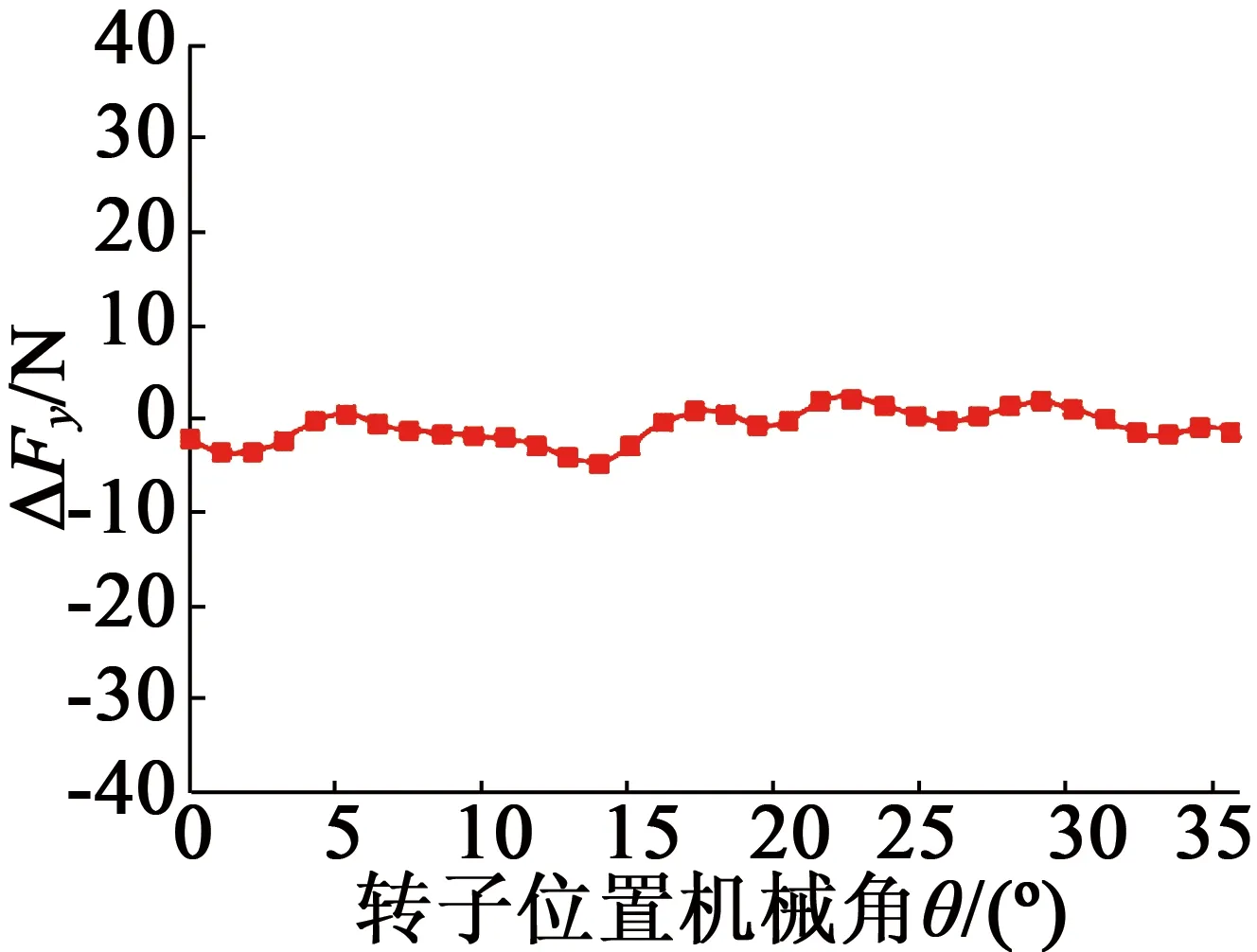
(d) y方向懸浮力計算誤差

由圖7可知，理論計算結果與有限元仿真結果之間誤差很小；x，y方向懸浮力最大誤差均不超過4 N，誤差主要原因在于本文計算單凸極結構槽內磁導分布僅考慮其基波分量，忽略其高次諧波分量；解析模型成功計算出了電機懸浮力固有的很小的直流分量;理論與有限元仿真均表明，由于組成每相繞組的兩個線圈在空間上正交，x，y方向懸浮力存在30°電角度相位差。

5 結 語

本文將許-克變換應用到具有雙凸極氣隙的BFSPMM中，推導并構建了其轉矩及懸浮力解析數學模型，理論分析及有限元仿真結果表明：

1) 有限元仿真結果驗證了該解析模型的正確性，電機永磁磁鏈及x，y方向懸浮力正弦度高；

2) 電機x，y方向懸浮力相位存在固有的30°電角度相位差；

3) 電機x，y方向懸浮力均存在很小的直流分量偏置，可以借助所提數學模型對電機結構進行進一步的優化將其影響降至最小。