基于等效磁勢法的直線電動機磁場及推力分析

李 爭，史雁鵬，王蕾永，薛增濤，王群京

(1.河北科技大學，石家莊 050018；2.安徽大學,合肥 230601)

0 引 言

直線電動機自從被提出以來受到廣泛關注，它是一種將電能直接轉換成直線運動機械能而不需任何中間轉換機構的傳動裝置[1]，相比于將旋轉運動轉換為直線運動的設備而言，它具有先天的優勢，歐美等發達國家率先開始對直線電動機展開研究，我國對于直線電動機的研究雖然起步較晚，但是有很多國外的成功經驗可以借鑒，因此最近幾年我國對于直線電動機的研究發展速度很快。永磁電機具有結構簡單、推力密度大[2]、能源效率高等諸多優點，因此大部分電動設備制造商都采用永磁電機作為動力來源。永磁同步直線電動機結合了永磁電動機和直線電動機的優點[3]，現在正受到越來越多的重視。

相較于一般的有鐵心直線電動機，無鐵心直線電動機不存在齒槽效應，因此推力波動小得多。由于動子中沒有鐵心，使得動子質量較輕，因此動態加速性能很好。在利用有限元法分析直線電動機時，雖然結果準確，但計算速度較慢；解析法不僅速度快，而且可以直觀地得到電機重要部分尺寸與推力及磁場的關系，有助于對電機的結構進行優化。電磁場計算最常用的兩種方法是等效磁勢法和等效磁化強度法[3-4]，文獻[5]利用等效磁化電流法計算了無鐵心永磁直線電動機的磁場和推力，文獻[6]利用等效磁化電流法對有鐵心永磁直線電動機的磁場和推力進行了計算，文獻[7]提出了一種適用于直線電動機的永磁磁極等效方法即等效磁勢法。本文基于等效磁勢法對無鐵心永磁同步直線電動機的氣隙磁場和推力進行了分析，通過與有限元法計算結果對比，證明了其準確性。

1 直線電動機結構

雙邊無鐵心永磁同步直線電動機結構如圖1所示。

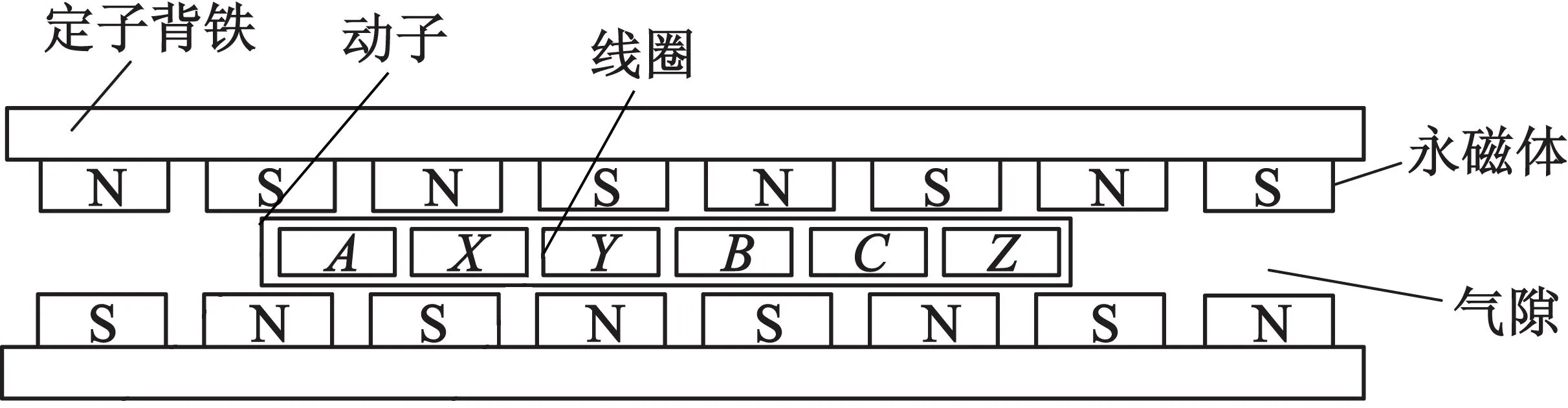
圖1 無鐵心永磁同步直線電動機結構圖

無鐵心永磁同步直線電動機由定子和動子組成，定子部分由永磁體和背鐵構成[3]，永磁體極性分布情況如圖1所示，由于上下側永磁體磁性相反，存在較大的法向吸力，所以永磁體需要通過強力膠固定在背鐵上，而且為了避免發生形變，定子長度不宜過長。動子內的三相繞組中沒有鐵心，利用環氧樹脂進行封裝固定，繞組內通入隨時間按正弦規律變化的交流電后產生行波磁場，與永磁體產生的靜磁場相互作用推動動子運動。由于動子是無鐵心結構，因此不存在齒槽力，端部效應也小得多，使得直線電動機不存在定位力，運行更平穩，電機繞組采用5極/3線圈結構，線圈之間排列緊密，能夠有效縮短動子長度，提高動子效率。

2 氣隙磁場分析

準確分析直線電動機的方法是建立電機的三維模型，但是三維模型的建立復雜而且求解方程的個數及維數較多，不利于分析計算[6]。為了簡化分析過程，將三維模型進行合理假設，簡化為二維模型進行計算，可作如下假設：

1) 直線電動機定子在x軸和z軸方向無限長；

2) 直線電動機鐵磁材料的磁導率無限大；

3) 忽略電機端部磁場畸變引起的端部效應。

根據如上假設，可以將復雜的直線電動機三維磁場求解問題簡化為二維磁場求解問題[8]。由于永磁同步直線電動機中的氣隙磁場幾乎全部由永磁體提供，所以在用解析法求解氣隙磁密時需要將永磁體進行等效。等效磁勢法的原理是將永磁體等效成無限薄的線圈，使該線圈產生的磁動勢與永磁體產生的磁動勢等效，將永磁體和氣隙組成的區域等效為一無源場[8]，在求解時用該線圈產生的磁動勢進行計算，永磁同步直線電動機等效磁勢法分析模型如圖2所示，δ為上下定子背鐵之間的距離，即氣隙高度。

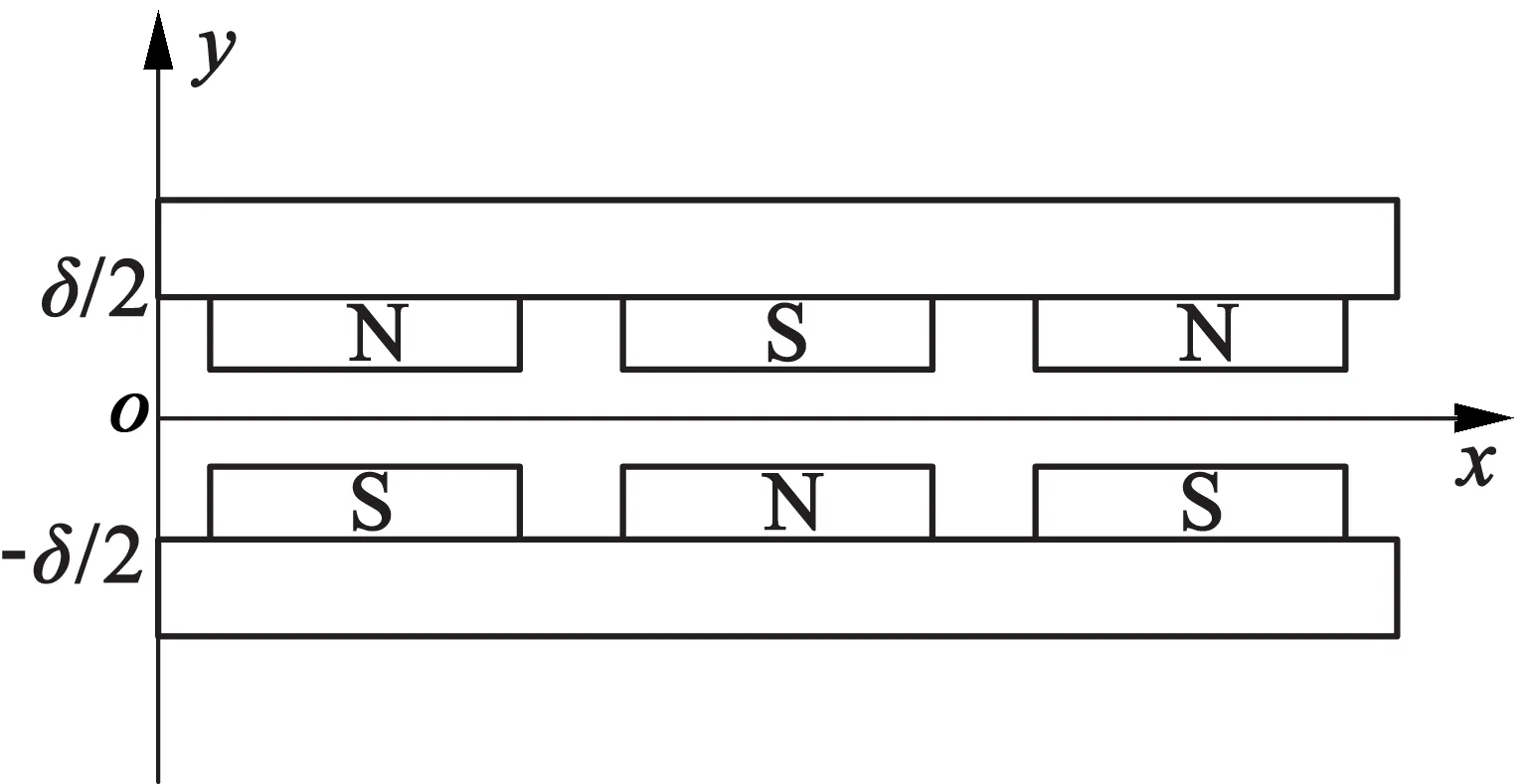
圖2 直線電動機分析模型

在假設成立的條件下，永磁體的磁勢空間分布情況如圖3所示，τ為直線電動機極距，τm為永磁體寬度，磁勢分布函數如下：

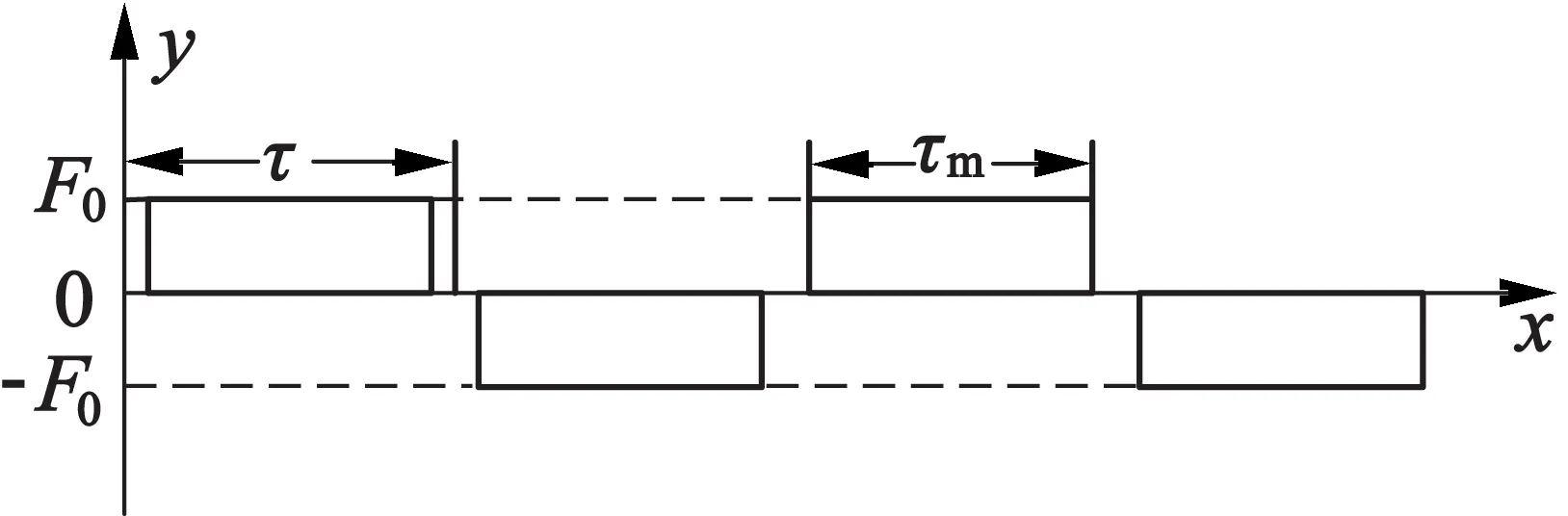
圖3 永磁體等效磁勢分布圖

k=0,1,2,3，…

(1)

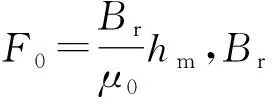
(2)

式中：

因為背鐵之間的區域被等效為無源場，所以其中的標量磁位滿足方程[9]：

(3)

利用變量分離法對方程求解得到方程的通解：

[Cksh(mky)+Dkch(mky)]

(4)

標量磁位關于x軸奇對稱[8]，即u(-x,y)=-u(x,y)，解得Bk=0，代入式(4),將原方程化簡：

(5)

根據假設(2)可得邊界條件：

(6)

將式(6)代入式(5)得到：

(7)

(8)

式中：

聯立式 (7)，式(8)解得：

Dk=0

(9)

(10)

將式(9)，式(10)代入式(5)中得到：

(11)

將標量磁位的通解分別對x，y求偏導,得到氣隙磁密在x，y方向上的分量：

sh(mky)·cos(mkx)

(12)

ch(mky)·sin(mkx)

(13)

3 有限元法驗證

為了驗證以上解析法得到的氣隙磁密表達式的準確性，建立了永磁同步直線電動機的二維有限元分析模型，對氣隙磁密進行求解分析。直線電動機的極距τ=16 mm，永磁體高hm=5 mm，永磁體寬度τm=13 mm，氣隙高度δ=19.6 mm，繞組高度hc=3.76 mm，得到的磁感線分布圖如圖4所示，氣隙磁密分布圖如圖5所示。

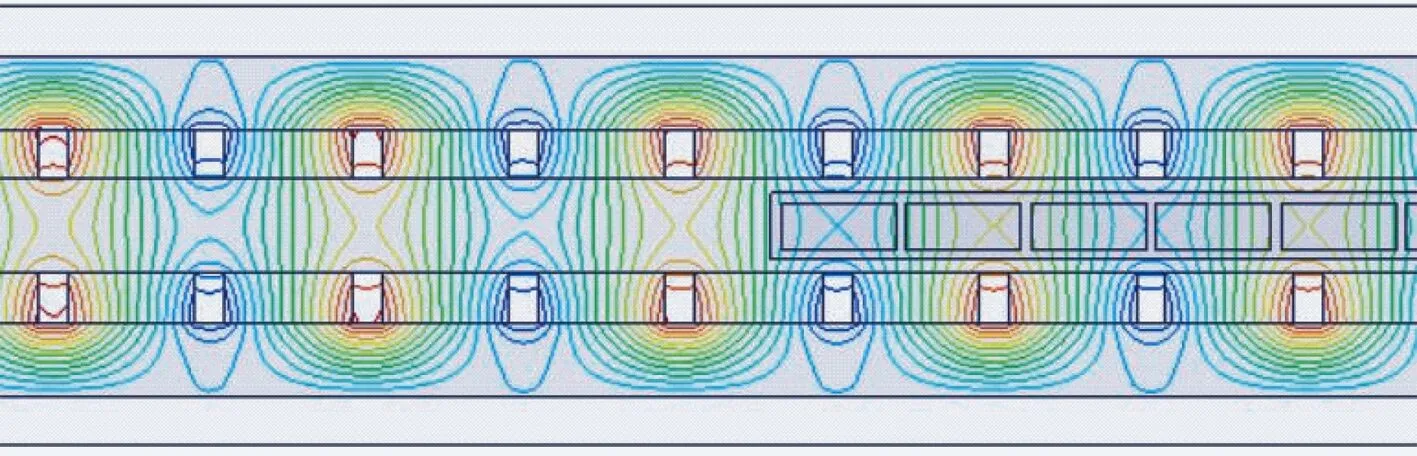
圖4 磁感線分布圖

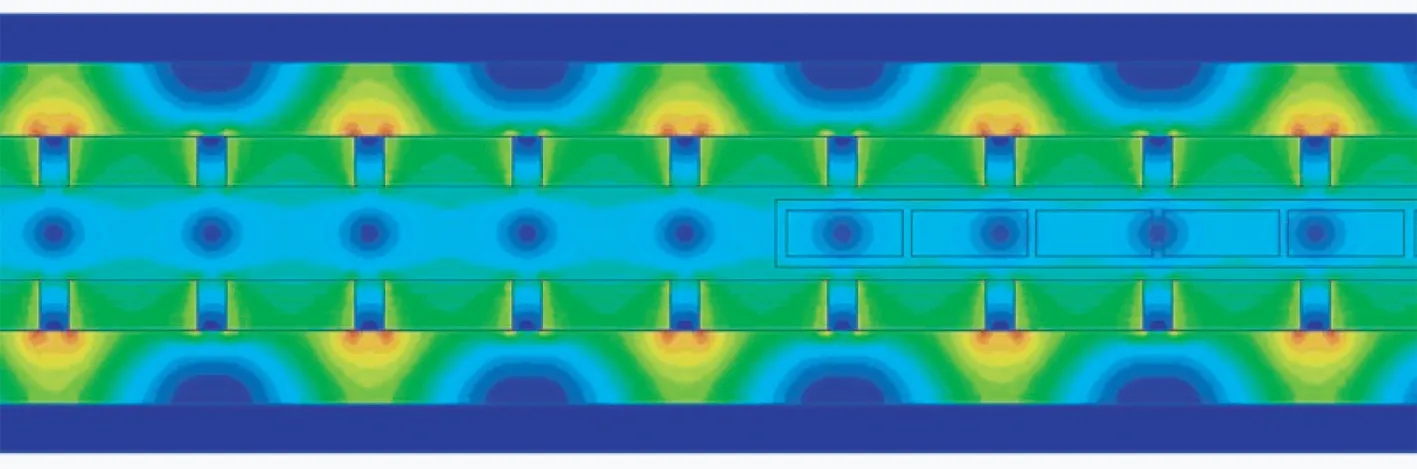
圖5 氣隙磁密分布圖

將y=0處解析法與有限元法得到的氣隙磁密進行對比，結果如圖6所示。由圖6可知，等效磁勢法的計算結果只在磁密曲線的波峰波谷出現明顯誤差，經計算的平均誤差為3.04%，精確度符合要求。y=2 mm處解析法與有限元法計算的氣隙磁密對比如圖7所示。兩種方法的計算結果平均誤差為3.53%，符合對準確度的要求。經計算后得到，當y≥3 mm時，等效磁勢法的計算結果會出現比較明顯的誤差，因此在本例中繞組的高度應控制在6 mm以內。推廣到其他的無鐵心永磁同步直線電動機，當繞組高度不超過氣隙空間高度的30%時，可以認為等效磁勢法計算得到的氣隙磁密表達式是準確的。在對直線電動機進行建模時，為了便于分析計算，將三維模型進行適當假設，簡化為二維模型，使得解析法的計算結果產生了一定誤差，但是由于誤差較小可以忽略，因此可以認為解析法的計算精度滿足要求。

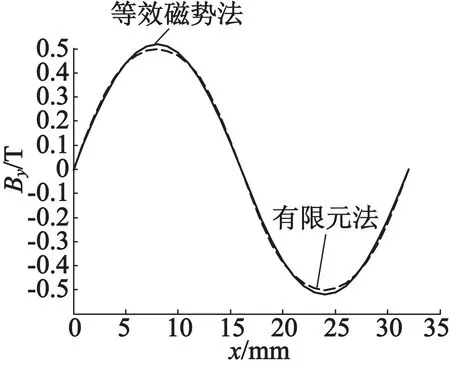
圖6 y=0處氣隙磁密分布圖

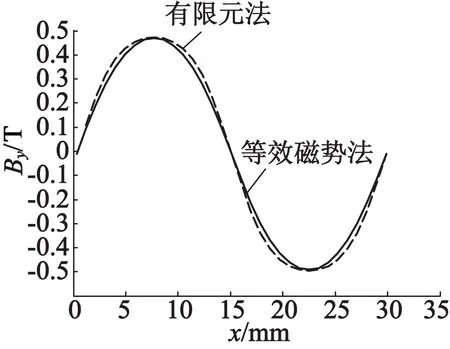
圖7 y=2 mm處氣隙磁密分布圖

4 直線電動機推力分析

直線電動機的推力是由永磁體產生的靜磁場和通有正弦交流電的繞組產生的行波磁場相互作用產生，可以通過直線電動機的氣隙磁密和繞組的電流密度計算得到。由于繞組為無鐵心結構，并且氣隙磁場幾乎全部由永磁體產生，所以電機不存在齒槽力且端部效應小得多。本文中直線電動機繞組采用5極/3線圈結構，其空間分布如圖8所示。

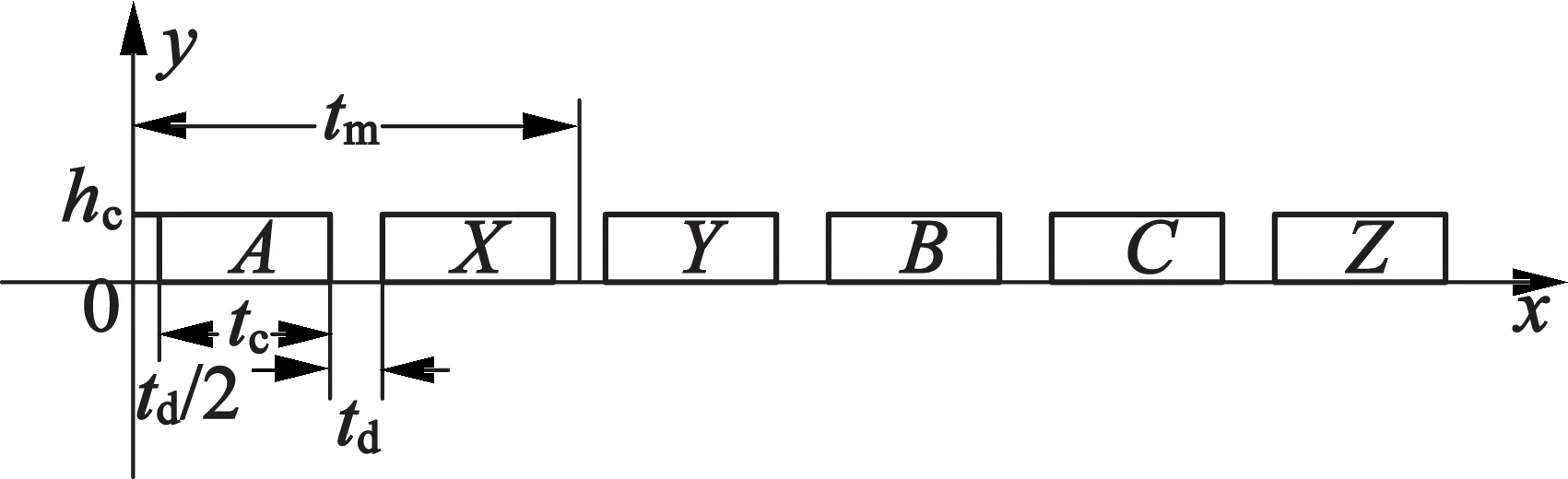
圖8 繞組空間分布圖

對應圖8的繞組空間分布圖，可以寫出直線電動機A相繞組的電流密度分布函數：

(14)

式中：

通過A相繞組的電流密度分布函數及氣隙磁密的公式可以得到A相繞組產生推力的微分形式：

dFxA=lcJaBydxdy

(15)

對應于圖8的繞組位置，A相繞組產生的推力：

(16)

式中：

將繞組的位置推廣到一般情況，當繞組在任意位置時將坐標原點由x0取代，A相繞組的電流密度分布函數如下式：

(17)

式中：

同理，可以得到B相，C相繞組的電流密度分布函數。

A相繞組產生的推力：

cos[mk(x0+tc)]

(18)

同理，可以得到B相，C相繞組的推力：

cos[mk(x0+tc+tm)]

(19)

cos[mk(x0+tc+2tm)]

(20)

式中：

將式(18)～式(20)整理后得到直線電動機繞組產生的總推力：

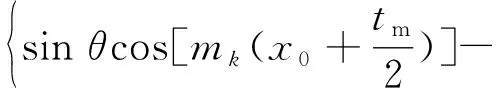
(21)

當電機繞組中的電流有效值為1 A時，用解析法和有限元法計算電機的推力，通過實驗測得推力數據，并獲得數據曲線，結果如圖9所示。在進行實驗時，首先將電動推桿和測力計固定，將測力計與上位機相連，打開與測力計配套的控制軟件，然后利用直線電動機勻速推動電動推桿，在軟件中記錄電機推力的變化曲線，實驗過程如圖10所示。從圖9中可以看出，有限元法計算的結果與實驗數據很接近，解析法求出的推力與兩者的結果存在一定誤差，經計算得到解析法的計算結果與有限元法及實驗數據的平均相對誤差為3.85%，可以認為計算的結果是準確的。由于直線電動機氣隙中的磁密大小不是按照標準正弦波進行分布的，而是存在一定數量的諧波，因此直線電動機在運動過程中會產生推力波動。從推力波動的角度看，電機的推力輸出比較平穩，解析法計算出的推力波動為±1 N，有限元法計算的推力波動為±1.2 N，實驗結果的推力波動為±1 N，證明解析法計算的結果是準確的。

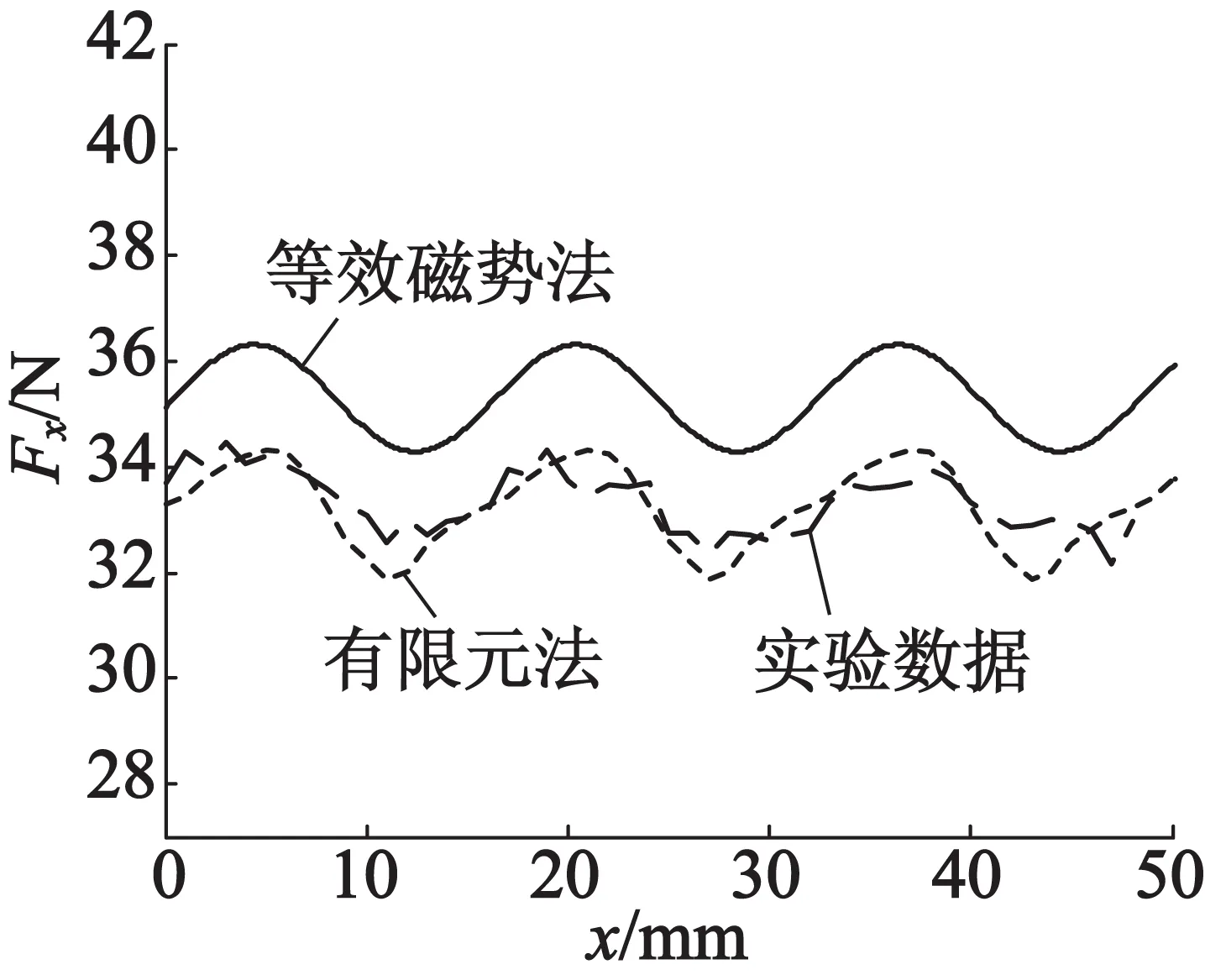
圖9 解析法、有限元法計算推力與實驗結果對比

5 結 語

本文采用等效磁勢法推導出了無鐵心永磁同步直線電動機的氣隙磁密和推力解析表達式，對其計算結果進行了分析，并建立了直線電動機的有限元分析模型，利用有限元法計算電機的磁場和推力，對比了兩種方法的計算結果，最后進行了直線電動機的推力實驗。通過計算得知，等效磁勢法的計算誤差在可接受的范圍內，驗證了磁密和推力解析公式的準確性。由于得到的磁密表達式不能保證在整個氣隙中都保持同樣的準確性，因此提出使用等效磁勢法時為保證精確度需要具備的條件，在無鐵心永磁同步直線電動機中，當繞組的高度小于氣隙高度的30%時，利用等效磁勢法計算出的直線電動機磁通密度和推力是較為準確的。