轉子斜極對永磁輪轂電機性能影響的研究
趙 玫,陳江岸,張云亮,劉亞帥
(1. 威海廣泰空港設備股份有限公司,威海 264200; 2.魯東大學,煙臺 264025)
0 引 言
在新舊能源加速轉換的當下,汽車動力從內燃機轉變為集中式的電驅動,未來將逐步發展為輪轂電機驅動。輪轂電機技術將車輪與電機整合到一起,省去差速器和傳動軸等傳統汽車的傳動裝置,真正實現能源的高效利用與車輛成本的有效較少。
文獻[1]設計出外轉子容錯永磁同步輪轂電機,將每個輪轂電機設計為多個子電機配合工作,同時設計出異型混合電機,滿足整個運行工況高效率運行。文獻[2]對永磁開關磁鏈電機的轉子進行斜極處理,分析不對稱徑向力、齒槽轉矩和反電動勢在轉子斜極后的變化情況,找到最佳斜極角度。文獻[3]針對雙凸極電機轉矩脈動較大的問題,對8極12槽外轉子雙凸極電機的轉子進行斜槽處理,通過有限元分析斜槽對轉矩與反電動勢的影響,最終達到優化電機性能的目的。文獻[4]設計了一種12/8極電勵磁雙凸極輪轂電機,在氣隙磁密、磁鏈、反電動勢等方面進行有限元仿真,得出其空載特性。文獻[5]為了研究不同繞組形式對電機性能的影響,設計了分數槽繞組電機與整距繞組電機,通過有限元計算出不同結構對電機磁密和反電動勢以及齒槽轉矩等方面的影響,得出在極對數合適的前提下,分數槽繞組的電機結構能有效減小電機轉矩脈動,優化電機性能。上述研究表明,設計出供車輛使用的高性能輪轂電機,是目前電機領域的熱點。為提高電機性能,需要在電磁設計方面考慮有較小的齒槽轉矩以及較接近正弦波的反電動勢。
本文針對機場擺渡車,設計一臺額定功率60 kW,額定轉矩2 500 N·m的外轉子表貼式永磁輪轂電機,較好地滿足機場擺渡車運行速度低、運行穩定性高的特點。首先給出電機的基本參數尺寸,其次利用有限元軟件計算了電機的空載特性和負載特性,最后分析永磁體斜極對電機齒槽轉矩、反電動勢和電磁轉矩的影響,綜合得出電機最優尺寸。
1 永磁輪轂電機主要尺寸
機場擺渡車用輪轂電機需要在高溫下運行,通常定子繞組溫度能達到200 ℃,轉子外殼溫度可達160 ℃。同時電機在轉速較低情況下要提供較大轉矩,并且要有較強過載能力,因此電機選擇直接將轉子安裝在車圈上的外轉子表貼式結構[6]。綜合考慮電機在機場擺渡車車輪中的應用,基本電機尺寸如表1所示。
2 永磁輪轂電機有限元計算
2.1 空載特性分析
圖1為空載時磁密云圖,時間為一個電周期。電機整體結構沒有出現嚴重飽和部分,只有定子齒尖有一定的飽和現象,齒尖少數部分的飽和對電機性能影響較小。圖2為氣隙的徑向磁密波形。磁密波形近似于方波,磁密最大達到0.81 T。在模型中,以圓心到定子齒長和定子軛厚度的一半為半徑分別建立路徑,得到定子齒部與定子軛部的磁密,如圖3和圖4所示。從圖3、圖4中可以看出,定子齒部磁密最大值達到1.32 T,定子軛部磁密最大值為0.96 T,基本滿足設計要求。

圖1 空載特性下的磁密云圖
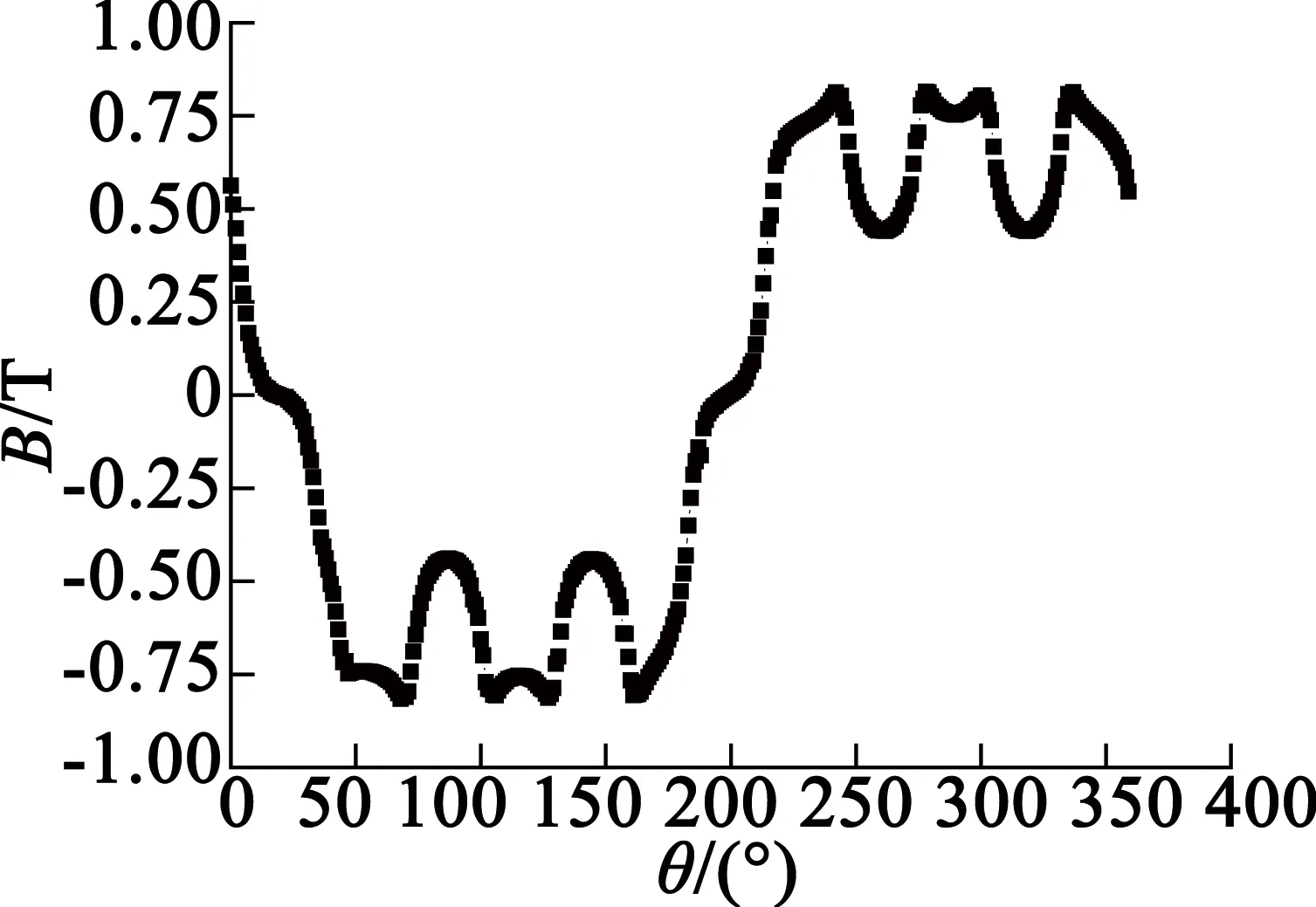
圖2 氣隙磁密波形
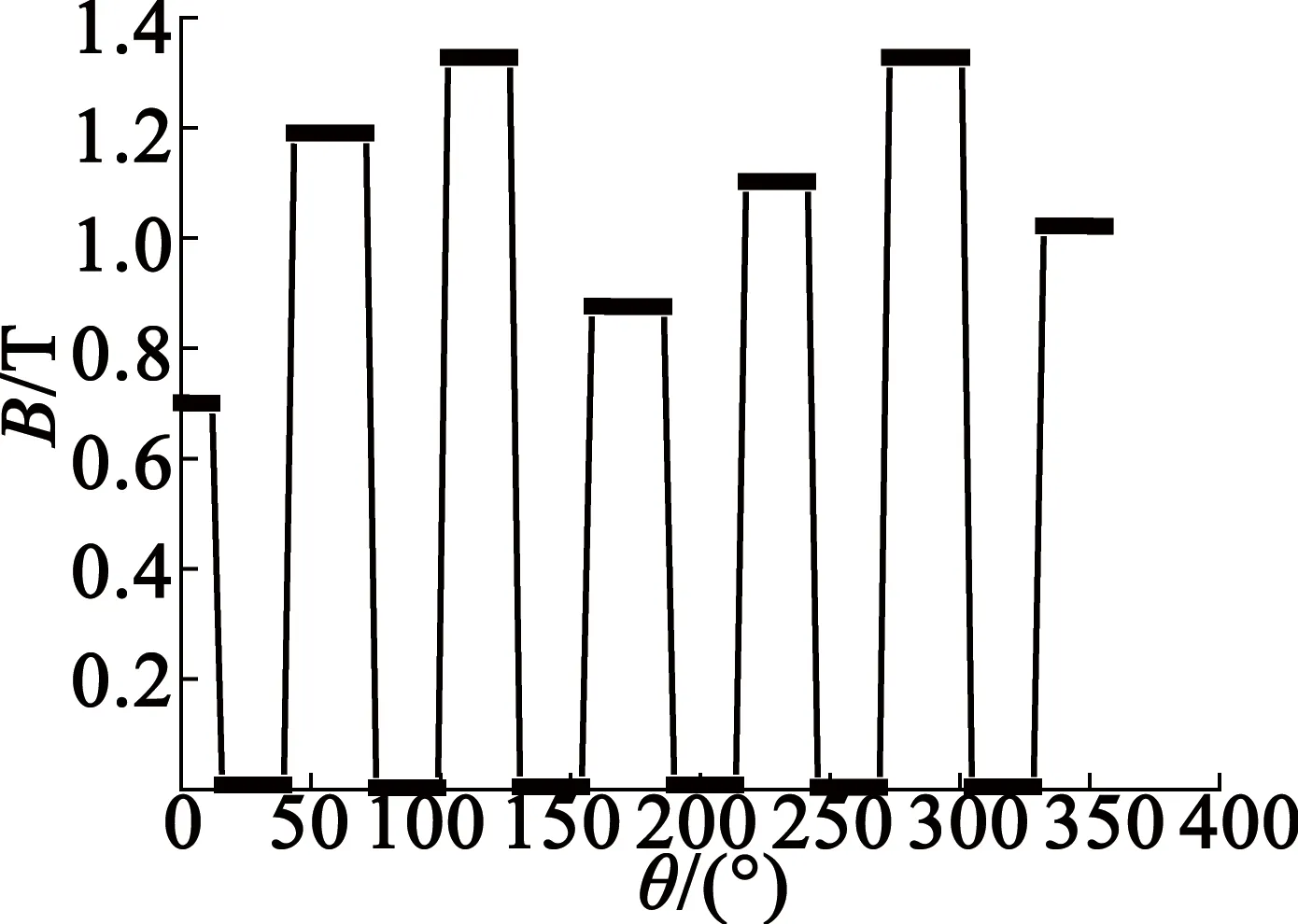
圖3 定子齒部磁密圖
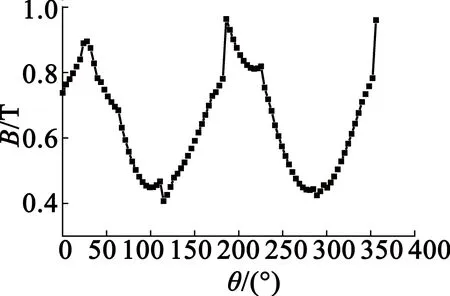
圖4 定子軛部磁密圖
圖5給出了空載條件下的三相繞組線電動勢波形,線電動勢幅值在280 V左右。圖6給出了齒槽轉矩波形圖,從圖6中可以看出,一個電周期的波動次數為66次,波動幅值為0.45 N·m,波動幅值較小。

圖5 空載線電動勢波形

圖6 齒槽轉矩波形圖
2.2 負載特性分析
定子繞組通入180 A電流時,電磁轉矩波形如圖7所示。電磁轉矩波動幅值為76 N·m,波動幅度較大,同時平均轉矩達到額定轉矩2 500 N·m, 電機各部分除齒尖外沒有出現飽和。圖8給出此時的線電動勢波形,可得線電動勢幅值達到335 V。
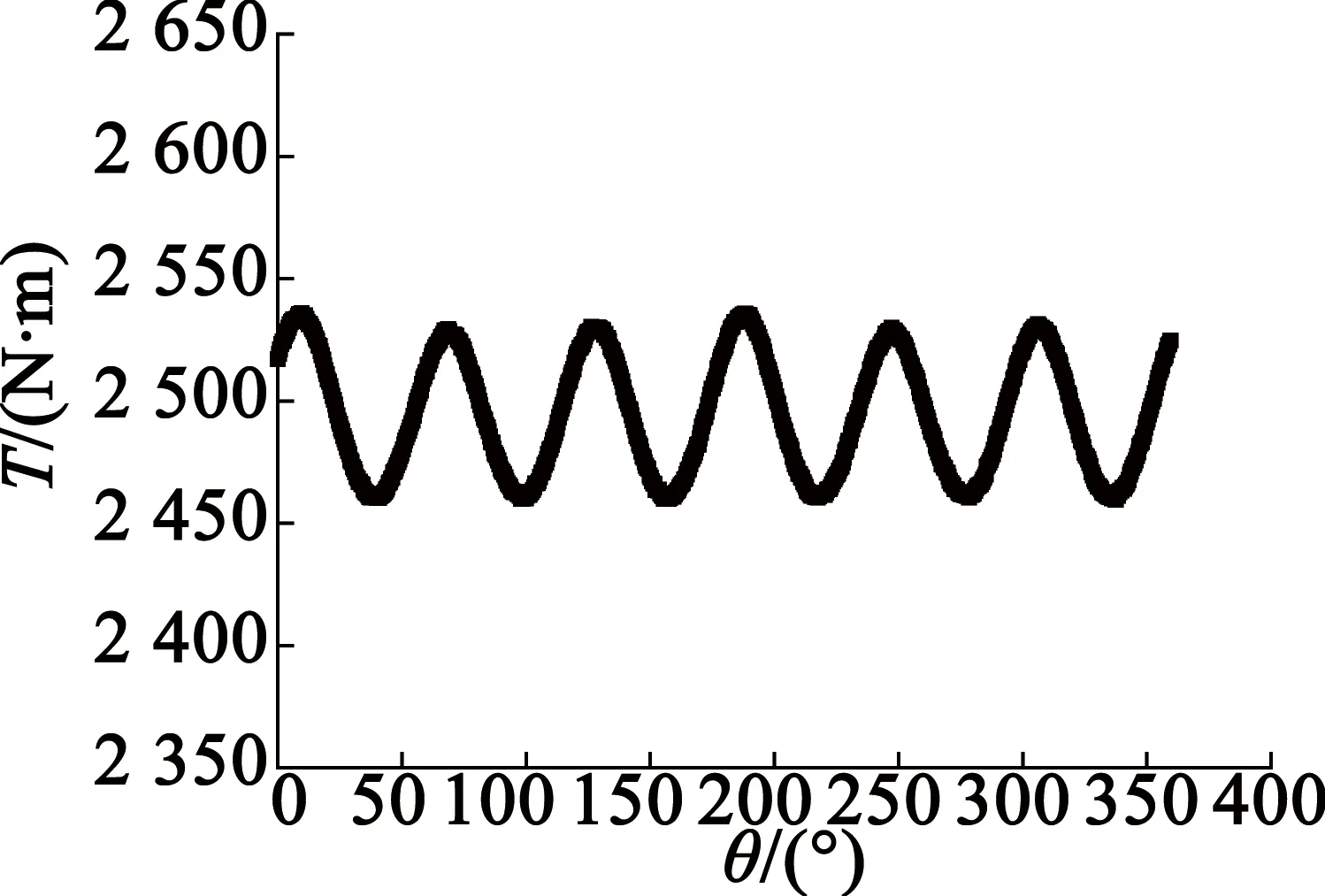
圖7 額定轉矩波形

圖8 三相感應電動勢波形
當定子繞組通入425 A電流,得到此時電磁轉矩波形,如圖9所示,此時達到最大輸出轉矩5 250 N·m,波動幅值達到170 N·m,波動幅值較大。圖10為通入425 A電流的線電動勢波形,幅值接近410 V,沒有超過最大電壓。圖11為電磁轉矩平均值隨電流變化曲線。從圖11中可以看出,隨著電流的增大,電磁轉矩近似呈線性增長。
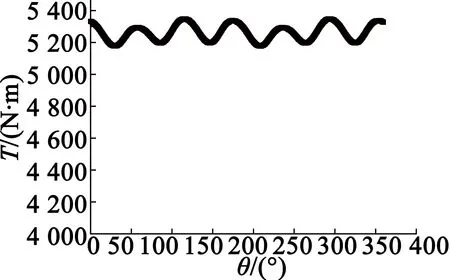
圖9 最大輸出轉矩波形
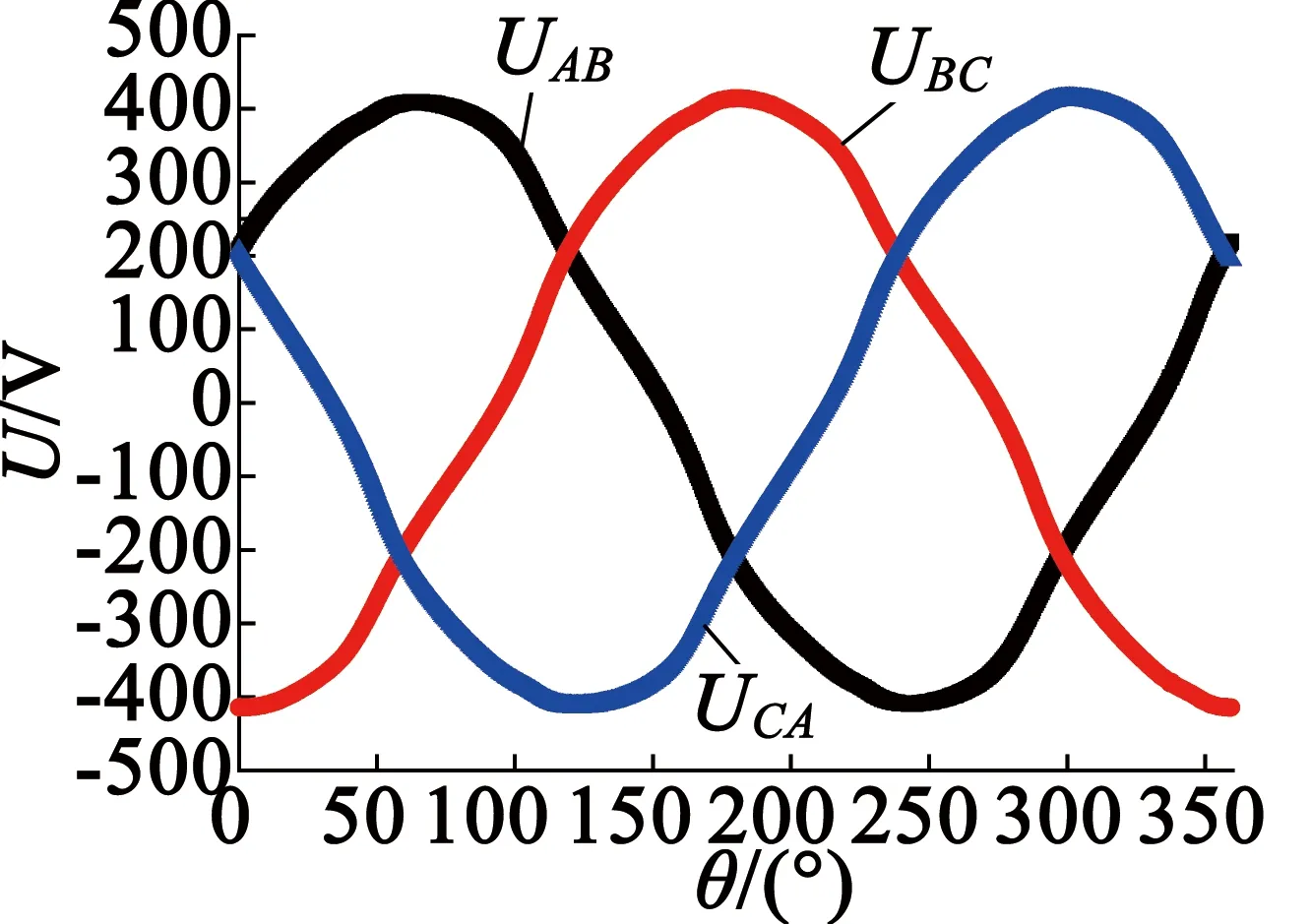
圖10 三相感應電勢波形

圖11 電磁轉矩平均值隨電流變化曲線
3 永磁輪轂電機性能的優化
機場擺渡車屬于地面服務特種車輛,每次承載乘客較多,為了使乘客有舒適的乘車體驗并感受到優質的服務水平,對車輛運行的穩定性要求較高[7]。由于齒槽轉矩是造成電機波動的主要因素,因此提高擺渡車性能,需要對齒槽轉矩進行抑制。空載反電動勢同樣影響永磁同步電動機的性能。通常永磁電動機的反電動勢含有高次諧波,導致波形偏離正弦波,降低控制精度,增加損耗和轉矩脈動,造成電機效率下降。因此,削弱電機反電動勢中的諧波對提高電機的性能具有重要的意義。
3.1 斜極對齒槽轉矩的影響
在引入斜極之后,電機靜態特性發生變化,電機軸向的不同截面的磁場分布是不同的,數值計算模型原則上采用三維模型。但三維電磁場分析時間較長,占用計算資源較大,因此仍傾向使用二維數值模型,通過分段計算法進行分析[2-3]。
其思路是沿電機軸向平均分成若干段,并把每段假設為一個電機,取其二維截面,從而將每段都作為二維模型處理,每一段的電磁場垂直于電機軸向,矢量磁位只有軸向分量。永磁體的斜極模型如圖12所示。

圖12 永磁體斜極模型
圖13為不同永磁體傾斜角度下的齒槽轉矩波形,圖14為齒槽轉矩波動幅值隨永磁體傾斜角度的變化曲線。從圖14中可以看出,當傾斜角度α為4°時,齒槽轉矩波動幅值較小;當傾斜角度α為3°時,齒槽轉矩波動幅值較大,達到0.902 N·m。最大波動幅值與最小波動幅值相差0.453 N·m。可見,永磁體斜極對齒槽轉矩的影響較小。
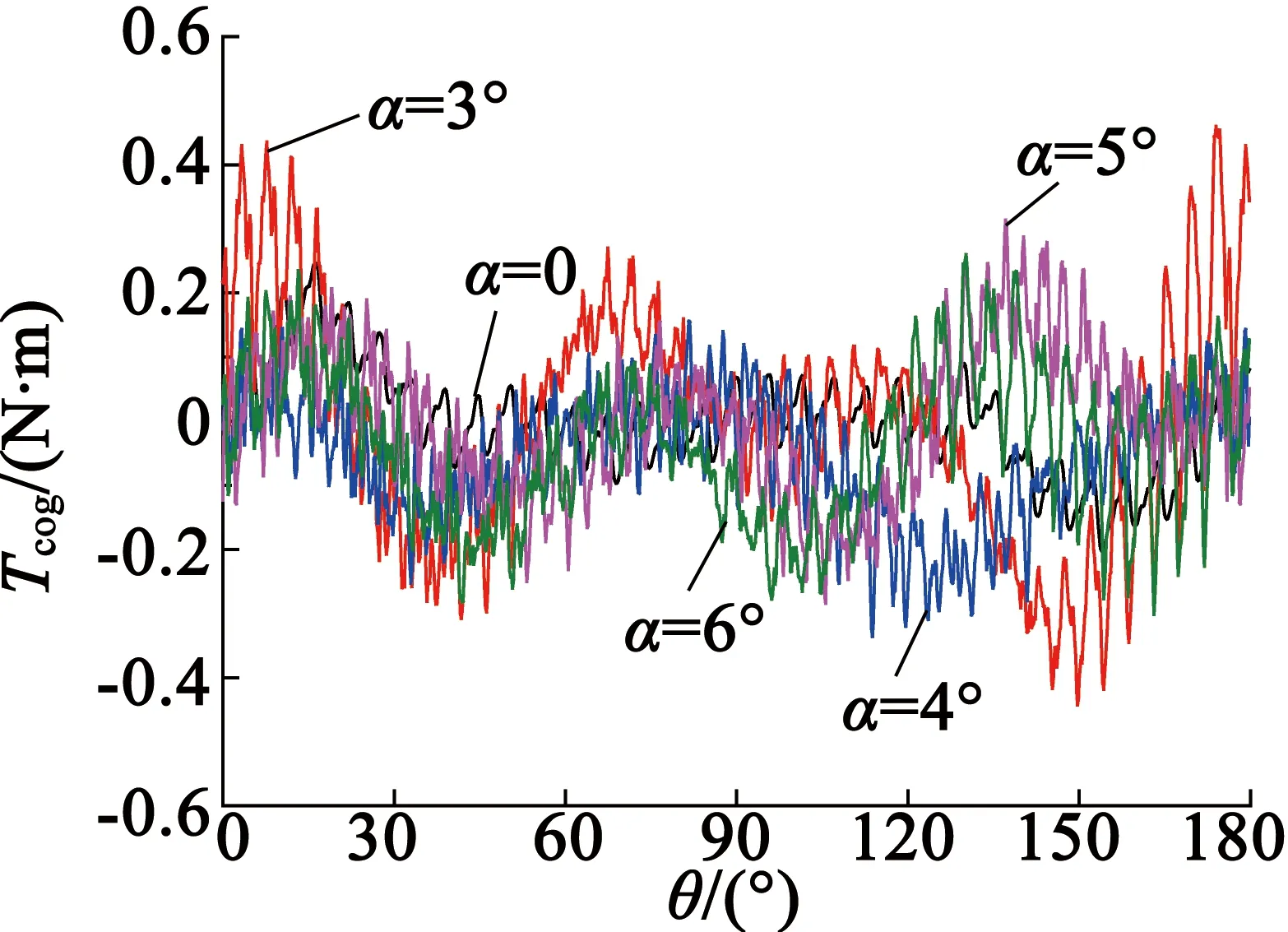
圖13 不同永磁體傾斜角度下齒槽轉矩波形
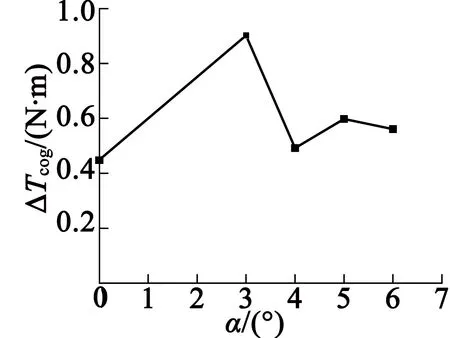
圖14 波動幅值隨永磁體傾斜角度的變化曲線
3.2 斜極對反電動勢的影響
為了更清晰地分析斜極對電機反電動勢的影響,本文定義空載反電動勢非正弦度系數αE,其在數值上等于反電動勢各諧波幅值的絕對值之和與基波幅值之比。
(1)
電機轉矩波動中主要是6次諧波,為了減小波動轉矩對電機性能的影響,這里首先定義波動轉矩系數αT6:
αT6=
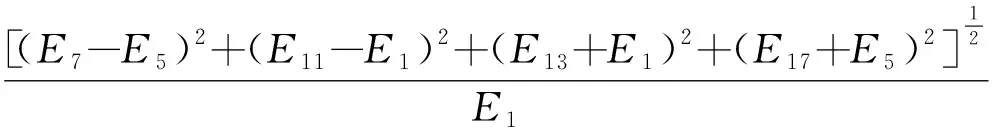
需要說明的是,上述公式推導忽略了電樞反應對波動轉矩的影響,即不考慮定子磁鏈所產生的波動轉矩以及忽略磁場飽和對波動轉矩的影響。轉矩波動主要是由反電動勢和電流的各次諧波相互作用產生的,而本文接下來只對由反電動勢5次和7次諧波所引起的轉矩波動展開研究,關于由電流諧波造成的轉矩波動和高于6次諧波引起的轉矩波動不予考慮。
因此,反電動勢非正弦度系數式(1)和波動轉矩系數式(2)可以簡化:
(3)

反電動勢隨傾斜角度變化結果如圖15所示。可以看出,不同傾斜角度時,反電動勢的幅值和相位都發生了明顯變化。
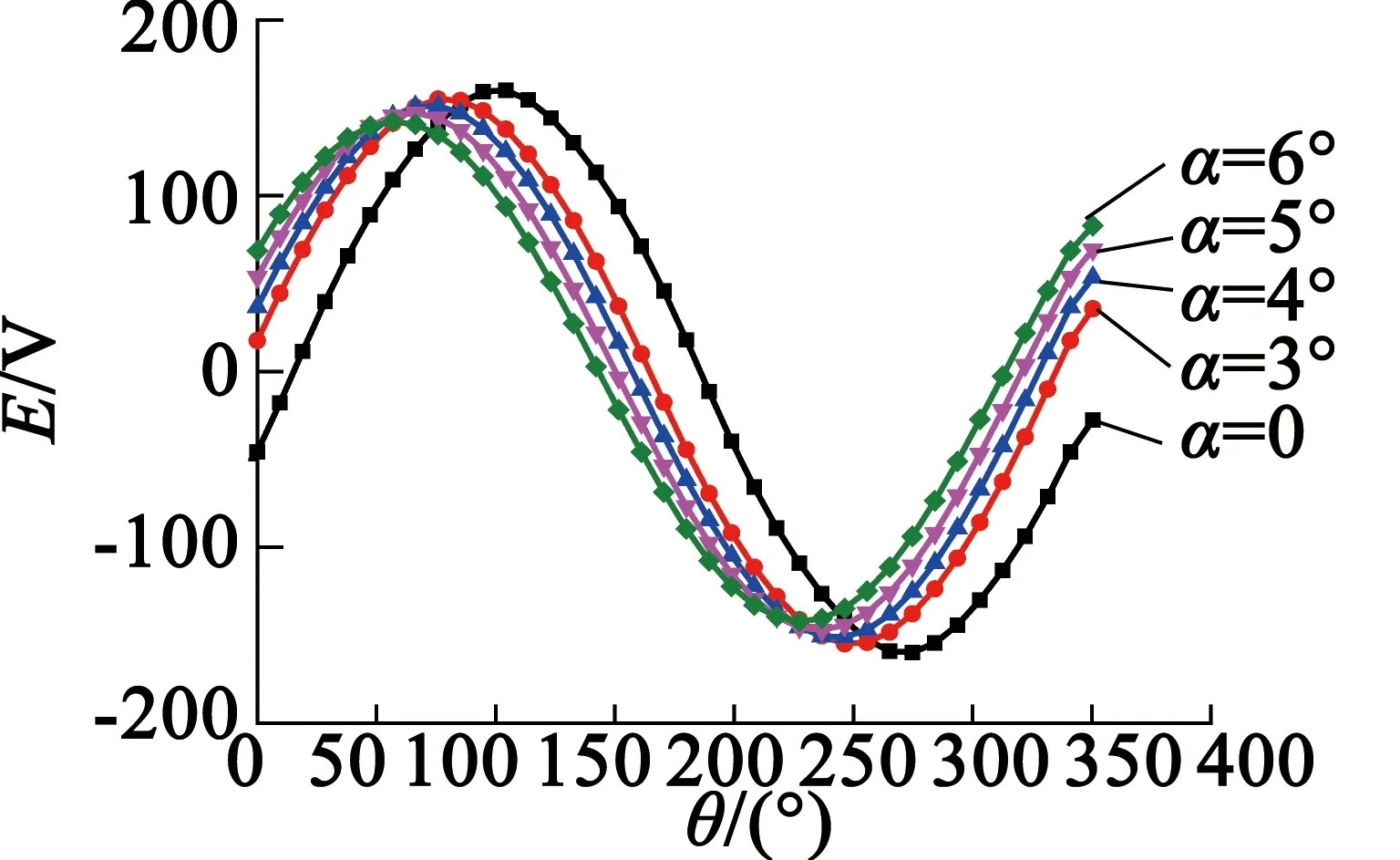
圖15 不同永磁體傾斜角度下反電動勢波形
通過對反電動勢傅里葉分解,得到反電動勢各次諧波隨永磁體傾斜角度的變化情況,如圖16所示。表2分別給出了在不同永磁體傾斜角度下反電動勢基波幅值、波動轉矩系數和非正弦度系數的對比結果。可知反電動勢基波隨永磁體傾斜角度的增加逐漸減小;當傾斜角度為4°時波動轉矩系數最小,與最大值相差較大;隨著傾斜角度的增加,非正弦度系數呈逐漸下降的趨勢。
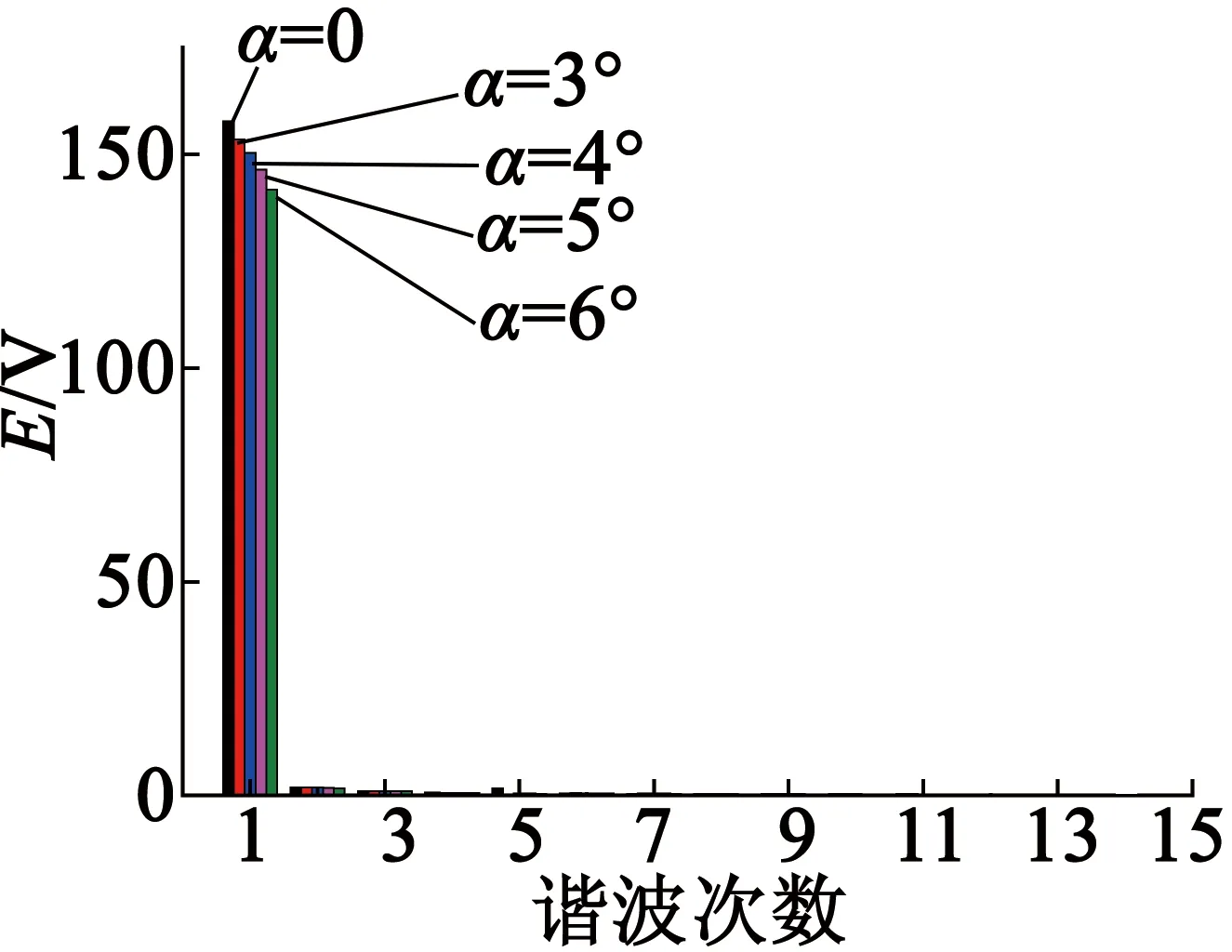
圖16 反電動勢各次諧波隨永磁體傾斜角度的變化情況

傾斜角度α/(°)03°4°5°6°基波E1/V161.676 8153.486 7150.271 9146.364 9141.686 8波動轉矩系數αT0.008 3980.001 2650.000 1180.000 5030.000 217非正弦度系數αE0.056 1440.049 5270.049 3950.048 6160.045 855
3.3 斜極對電磁轉矩的影響
當電機通入300 A電流時,得到不同永磁體傾斜角度下電磁轉矩在一個電周期內的波形圖,如圖17所示。從圖17中可以看出,隨永磁體傾斜角度的增大,電磁轉矩幅值明顯下降。圖18為電磁轉矩波動幅值隨傾斜角度的變化曲線。可以看出,斜極對電磁轉矩的波動具有明顯的抑制效果,但當傾斜角度大于5°時,斜極對轉矩波動的抑制效果明顯減弱;同時,隨著傾斜角度的增大,電磁轉矩幅值下降較快。因此,對電機進行斜極設置時,傾斜角度不能太大。為此,本文最終選取永磁體傾斜角度為4°,既保證電磁轉矩足夠大,又保證轉矩波動幅值較小。
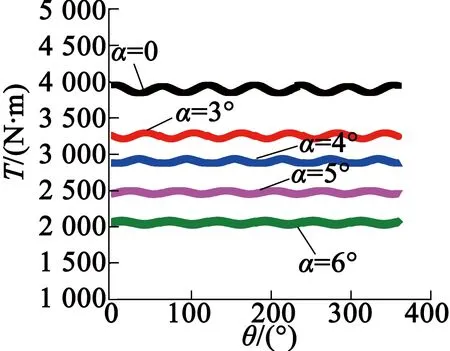
圖17 不同永磁體傾斜角度下電磁轉矩波形
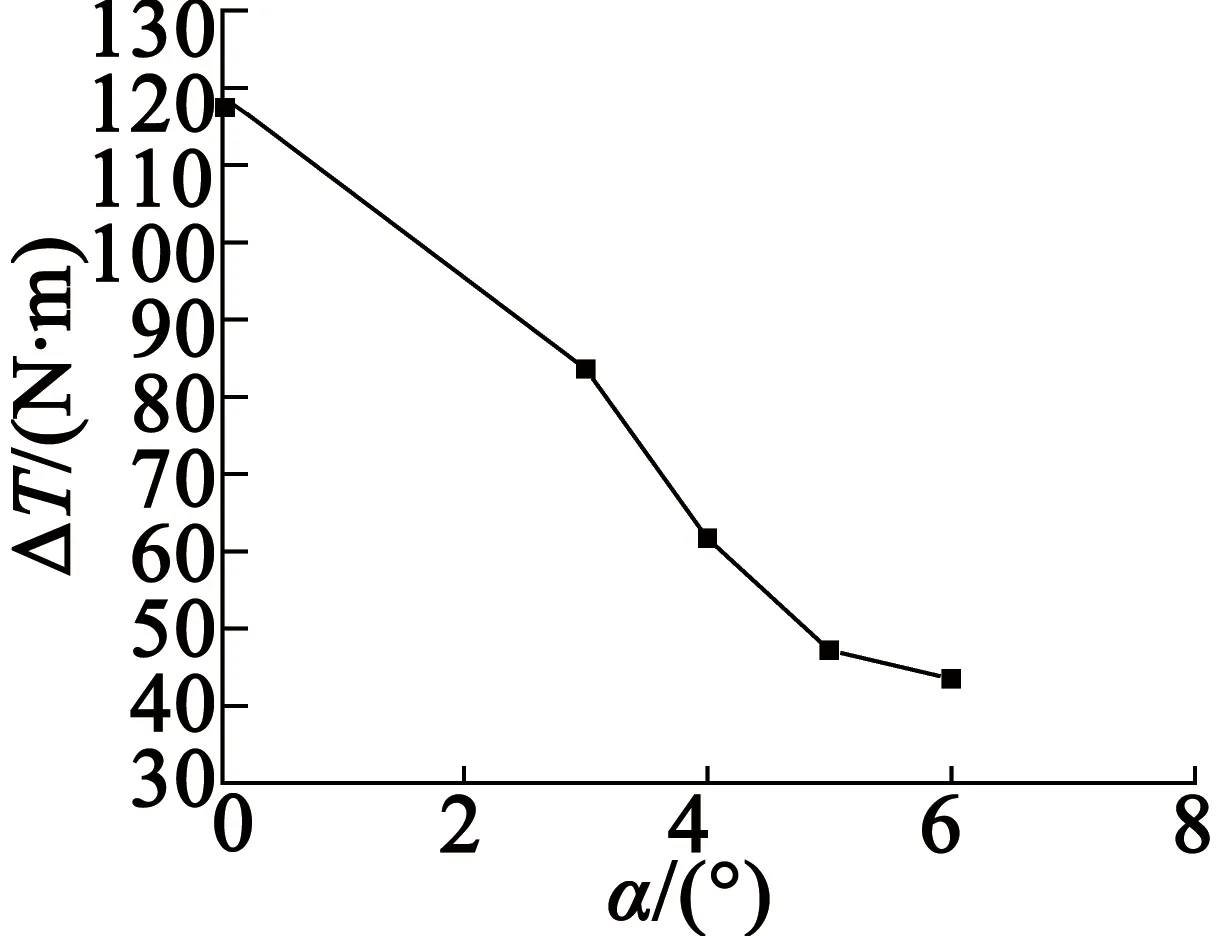
圖18 電磁轉矩波動幅值隨傾斜角度的變化曲線
4 結 語
本文根據機場擺渡車的應用特點,設計出30極99槽永磁同步輪轂電機,主要完成了以下4方面工作。
(1) 為了使永磁同步輪轂電機滿足機場擺渡車的性能要求,通過有限元軟件對設計的電機進行了空載特性與負載特性分析。
(2) 通過有限元軟件計算了轉子斜極對齒槽轉矩的影響,得出當永磁體傾斜角度為4°時齒槽轉矩幅值最小。
(3) 通過有限元軟件計算了轉子斜極對反電動勢的影響,得出反電動勢基波幅值隨著傾斜角度的增加而下降。波動轉矩系數隨著永磁體傾斜角度的增加逐漸減小,當傾斜角度為6°時,非正弦度系數最小。
(4) 通過有限元軟件計算了轉子斜極對電磁轉矩的影響,最終本文選取永磁體斜極4°作為所設計的永磁輪轂電機轉子斜極的最佳角度。

