我國物流景氣指數(LPI)預測模型的構建及分析
(福州大學 經濟與管理學院,福建 福州 350000)
1 引言
作為經濟發展的一個新增長點,物流業被稱作經濟增長的“加速器”,經濟增長帶動物流業的發展,同時物流業對促進經濟增長具有不可磨滅的作用,物流業通過整合資源、優化配置、創造價值為各大企業帶來高額利潤,被稱作“企業腳下的金礦”[1]。由圖1可知,2003到2017年中國社會物流總額從19.54萬億元上升到252.8萬億元。其中,2016年我國社會物流總額229.7萬億元[2],同比增長6.1%。2017年我國社會物流總額252.8萬億元,同比增長6.7%,社會物流總額呈現逐年上升趨勢。可以看出,我國物流業將近20年來一直快速發展且物流需求在經濟增長的帶動下規模逐漸擴大,物流業的未來發展存在著較大提升空間。然而物流業的發展一直以來都處在一個動態變化過程,通常人們采用物流景氣指數(LPI)來衡量一國物流業整體的發展狀況,物流景氣指數(LPI)綜合考慮社會物流總額、社會物流總費用、訂單交易量及貨運量等不同指標,加以計算分析以求得物流景氣指數(LPI)數值,本文通過中國指數網每月發布的物流景氣指數(LPI)數據,對這一指標進行建模分析,擬合原始序列,找到最佳的預測模型,以此分析未來物流景氣指數的數值波動變化,有助于衡量我國物流業未來的發展態勢,對國家宏觀經濟政策的制定有著重要參考價值。
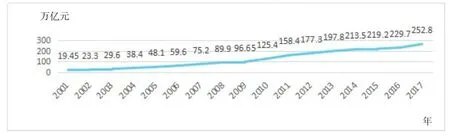
圖1 2003-2017年中國社會物流總額變化趨勢圖
2 預測模型及數據選取
2.1 灰色GM(1,1)預測模型
2.1.1 事前檢驗。為了保證合理建模和模擬實驗的成功,需要對原始序列進行事前檢驗[3],即:
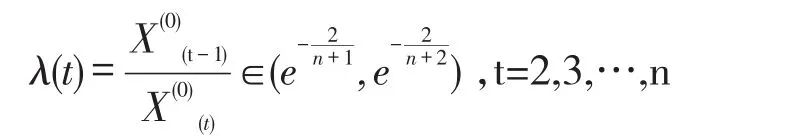
若計算數據級比λ(t)滿足可容范圍,則可進行灰色GM(1,1)預測,反之則需對原始數據做變換處理,確保選取的數據全部落入可容范圍內。
2.1.2 模型建立
(1)記原序列X(0):

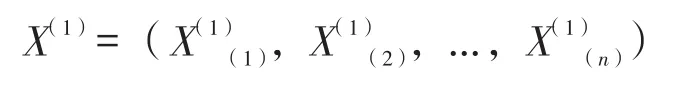
(2)生成X(1)的緊鄰均值序列:

(3)對生成序列X(1)建立如下白化微分方程并求解:
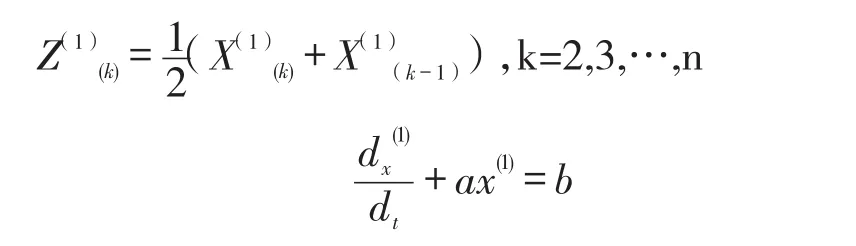
其中,-a稱之為發展系數,反映出擬合值的發展態勢,b稱之為灰色作用量,反映出數據的變化關系。
(4)求解白化微分方程,得到時間響應序列為:
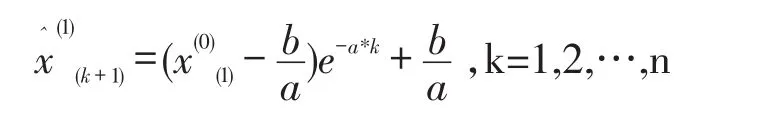
2.2 BP神經網絡預測模型
BP神經網絡,即多層前饋神經網絡,它由輸入層、隱含層和輸出層組成,其網絡結構如圖2所示。
BP算法主要分為前向傳遞和反向傳遞兩個過程[4]:在前向傳遞中,信號經輸入層、隱含層、輸出層逐層處理并傳遞,檢查預測輸出與給定輸出之間的誤差,若沒有達到精度要求,則轉入反向傳播。在反向傳遞中,根據檢測到的誤差來調整輸入層與隱含層之間的權值和閾值,從而使預測輸出不斷逼近期望輸出。
基于MATLAB的BP神經網絡學習過程如圖3所示。

圖2 BP神經網絡結構
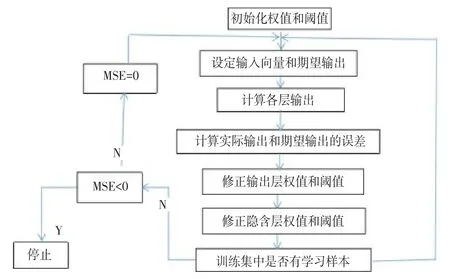
圖3 BP神經網絡MATLAB算法流程圖
2.3 ARIMA預測模型
ARIMA模型即綜合自回歸移動平均模型,簡記為ARIMA(p,d,q)模型,其中AR是自回歸,p為自回歸階數,MA為移動平均,q為移動平均階數;d為時間序列成為平穩時間序列時所做的差分次數。ARIMA(p,d,q)模型的實質就是差分運算與ARMA(p,q)模型的組合,即ARMA(p,q)模型經d次差分后,便為ARI-MA(p,d,q),模型建立[5]如下:
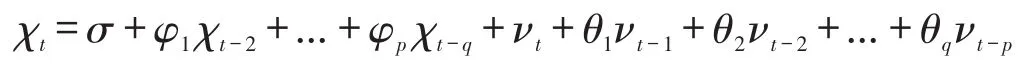
其中,νt為白噪聲序列,p,q是滯后階數,引入滯后算子,記為S,進一步得到表達式為:
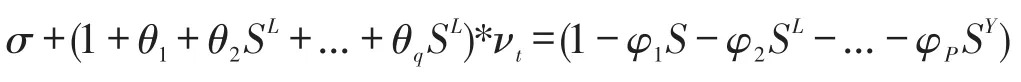
建立ARIMA模型的步驟:
(1)對被觀測時間序列數據進行繪圖,判斷是否為穩定時間序列;
(2)對非平穩序列進行D階差分轉換使其成為平穩序列;
(3)對處理后的平穩序列進行ACF和PACF計算,通過自相關和偏相關圖對模型進行定階;
(4)對所建立的模型進行分析評價。
2.4 原始數據的選取
本文通過中國物流與采購聯合會網站和中國指數網每月5日發布的LPI往來數據,整理統計從2013年8月到2018年7月以來的物流景氣指數變化數據,每月數據見表1。

表1 2013年8月-2018年7月LPI統計數據表
3 數據建模分析
3.1 灰色GM(1,1)預測模型
3.1.1 事前檢驗。為了順利建模,并保證模型的可行性,需通過級比檢驗法做預測事前處理[2]。
經計算,原始數據的可容量范圍為:λ(t)∈(0.95,1.07),檢驗數據可進行均值灰色GM(1,1)模型預測。
3.1.2 模型計算。根據灰色預測模型的方程,利用MATLAB進行矩陣計算,求得灰色GM(1,1)預測的發展系數-a為0.000 34,灰色作用量b為54.708,平均相對誤差3.39%,計算得知2013年8月到2018年7月以來的真實值和預測值擬合趨勢見表2和圖4。
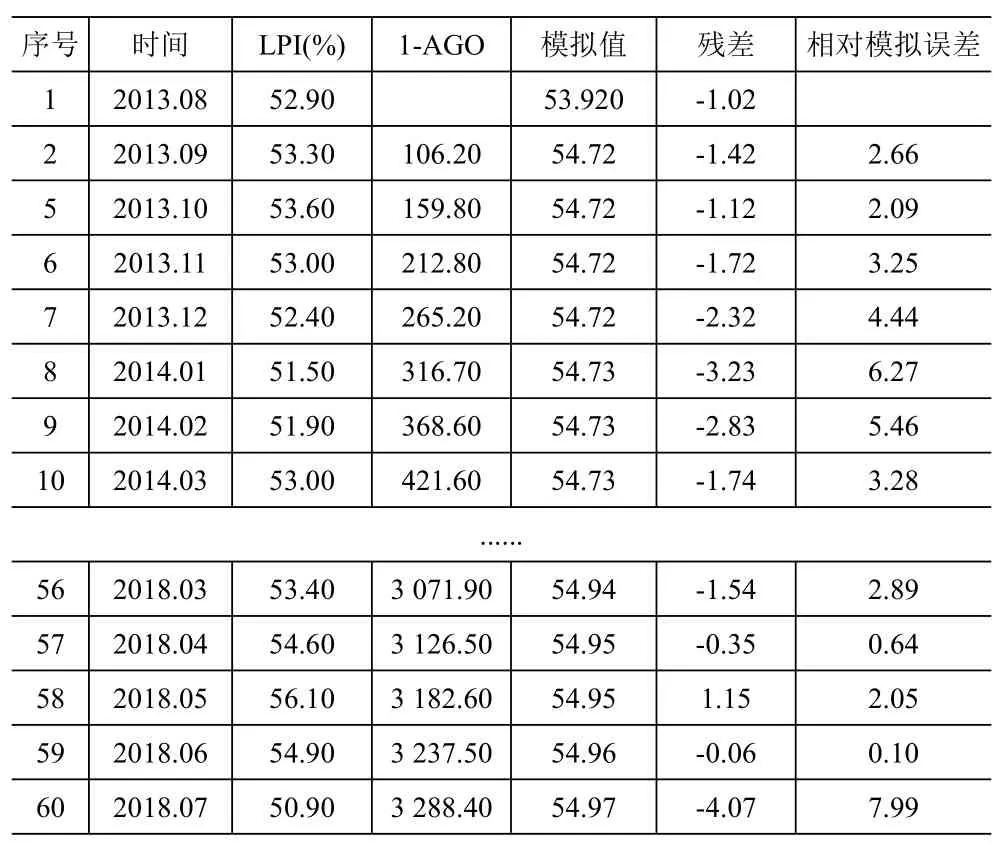
表2 灰色GM(1,1)預測的真實值與預測值比較分析
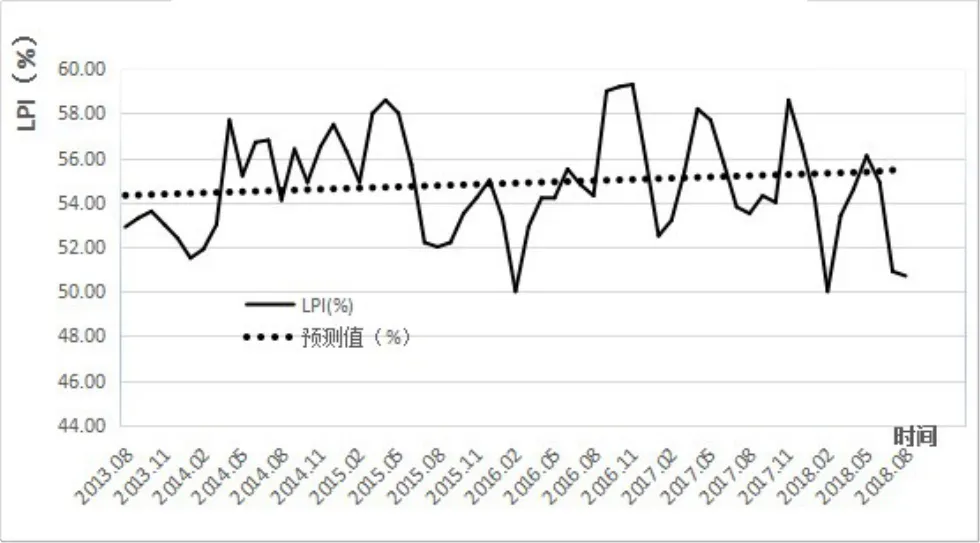
圖4 灰色GM(1,1)模型下數據擬合圖
由圖4可知,通過灰色GM(1,1)模型預測2013年8月到2018年7月這60個月以來的預測值和真實值偏差過大,原始序列呈不穩定的波動而預測模型得到的擬合數據呈現穩定趨勢,其中在2018年2月LPI的預測值和真實值的誤差高達7.99%。說明灰色GM(1,1)預測趨于持續穩定的數據變化,這也進一步看出灰色GM(1,1)預測對于時間序列跨距較長和多個數據預測的不合理性,它的預測優點就是對原始序列要求不高,對相對穩定的原始數據擬合較為準確,當原始序列不穩定,時間序列較長時,數據預測結果精準度反而會降低,預測誤差變大,所以需要進一步探討其他預測模型。
3.2 BP神經網絡預測模型
3.2.1 對原始數據的預處理。為了使原始數據在神經網絡預測模型中能夠合理運行,需要將收集來的數據進行歸一化處理。
Matlab程序主要代碼如下:
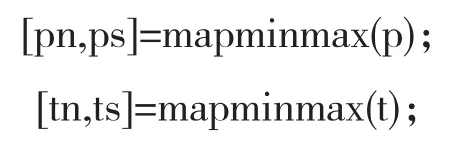
3.2.2 對網絡進行訓練

3.2.3 用訓練好的神經網絡進行預測[4]

3.2.4 預測結果。由圖5可知,通過MATLAB進行原始LPI的模擬得到擬合誤差為2.87%,圖中原始數值和BP神經網絡預測得到的數值存在一定的誤差,BP神經網絡預測得到的數據呈縮短間隔期的線性趨勢,預測的數據波動較大,對于時間序列周期很近的預測存在較大的偏差,由預測結果可以看出,在2014年2月到2015年3月幾乎呈線性上升狀態,而在2015年4月到2016年1月又出現持續下降狀態,之后又逐步上升,其中在2016年11月出現峰值為60.73,顯然與真實值存在很大偏差,由MATLAB進行訓練后得到未來數值的預測結果,如圖6所示。
由圖6可知,通過BP神經網絡預測未來幾期的物流景氣指數趨勢,在2018年8月后物流景氣指數將出現一定回升的趨勢,預測未來五期結果顯示為51.46、53.14、56.44、56.70、54.68,從預測數據可以看出,在2018年10月到11月將出現2018年末幾個月的極大值,但預測存在很大的殘差,需要對建模進一步探索。
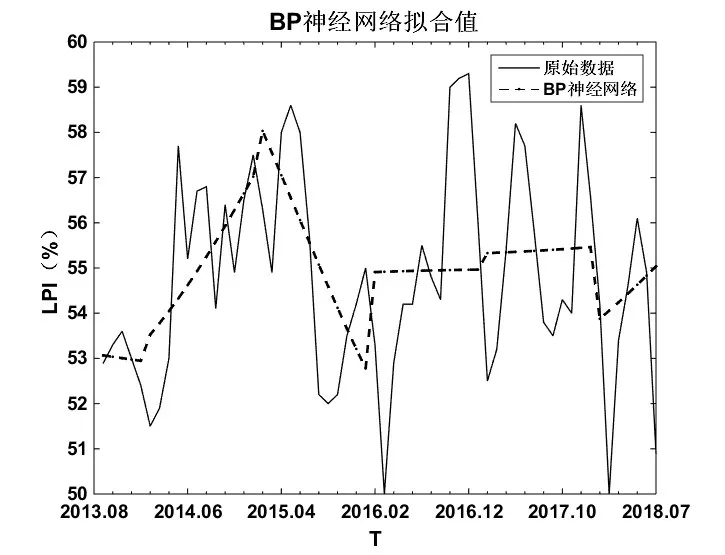
圖5 BP神經網絡預測的擬合趨勢圖
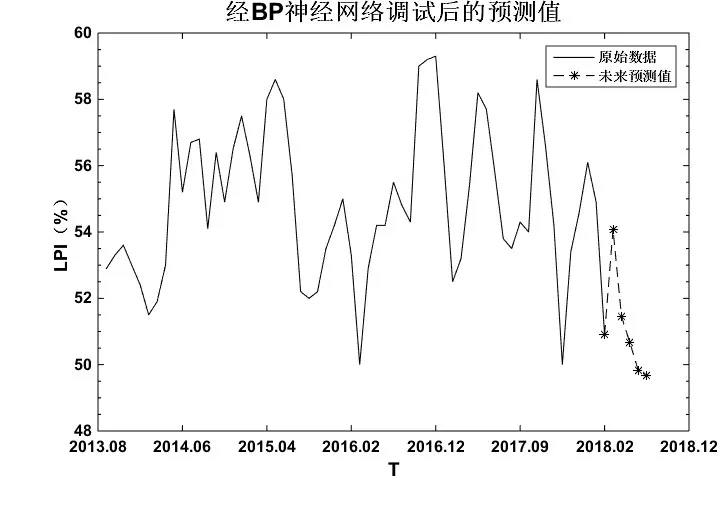
圖6 BP神經網絡預測未來趨勢圖
3.3 ARIMA預測模型
3.3.1 平穩性檢驗及模型定階。由圖7分布的散點圖可知,物流景氣指數(LPI)的值并沒有隨著時間序列呈現持續遞減或遞增變化,且沒有固定常數截距和穩定的周期性波動,所以需要對原始序列進行平穩性檢驗[1]。
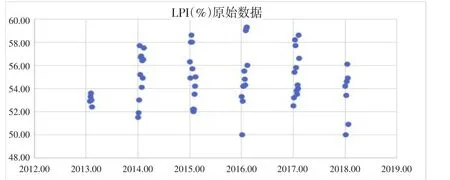
圖7 LPI的散點圖
通過ADF單位根檢驗方法來界定原始數據的平穩性,檢驗發現,原始序列LnLPI的ADF值為-2.932,大于置信水平5%的臨界值,P值為0.779,判斷原始序列存在單位根,即所選的LPI為非平穩性時間序列,對一次差分結果進行平穩性檢驗,輸出的自相關如圖8所示。
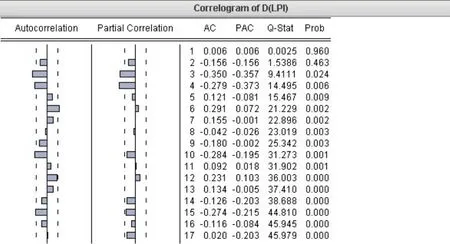
圖8 一次差分后的自相關圖

圖9 二次差分后的自相關圖
由此得到prob的值出現大于置信水平0.05,分別在第9階、第14階、15階、16階和第17階,所以對原始序列進行二次差分后得到的白噪聲序列屬于穩定序列[7],由圖10的二次差分后的序列圖也可以看出,除了在2014年5月、2018年1月和4月有明顯突出外,其余均處于較穩定波動。與原始序列圖比較可以看出,經過差分處理后的數據穩定性大大提高,因此界定參數d的值為2,接著對模型進行定階及參數估計。
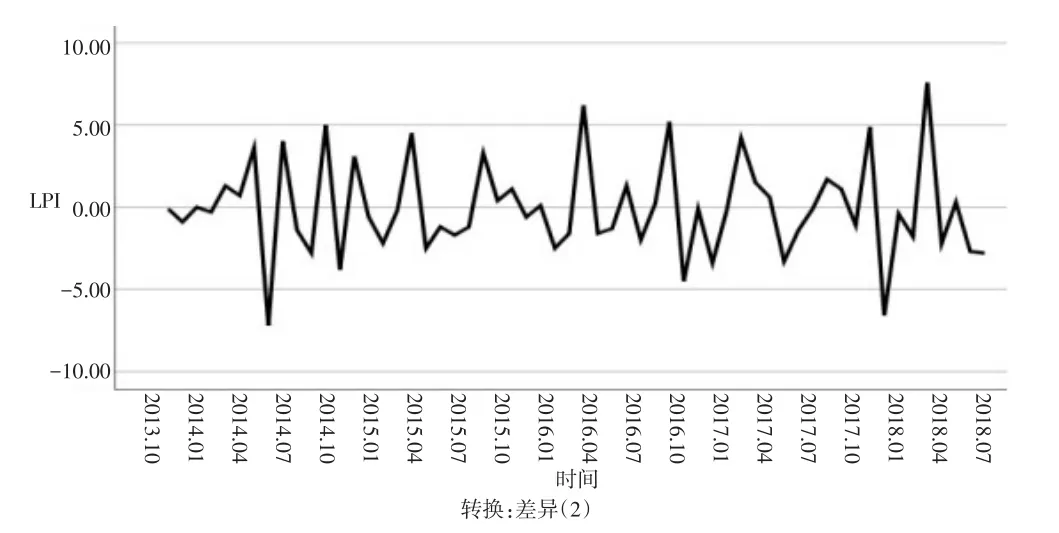
圖10 二次差分后的序列圖
由圖9可以得出,自相關AC在第一階的值為0.418,在第二階時變為0.009,因此自相關函數在滯后第一階變小,界定參數q的值為1,偏相關PAC在延遲第一階時數值為0.418,第二階變為0.201,在第四階又變為0.445,因此定自回歸階數P的值為1或者3。對模型ARIMA(1,2,1)和ARIMA(3,2,1)進行擬合度的比較結果見表3。

表3 兩種模型下的擬合數據比較
由表3可以得出,ARIMA(3,2,1)模型和ARIMA(1,2,1)模型下的均方根誤差RMSE的值比較為2.106>1.866,平均百分比誤差MAPE的值比較為2.874>2.413,通過BIC判斷準則,由表3中的正態化BIC的值比較為1.766>1.662,通過比較得知,ARIMA(1,2,1)模型擬合度要優于ARIMA(3,2,1)模型。
3.3.2 利用ARIMA(1,2,1)模型擬合原始數據。通過
3.3.1檢驗穩定性和模型定階后,利用ARIMA(1,2,1)模型進行原始數據的擬合估計,如圖11所示。
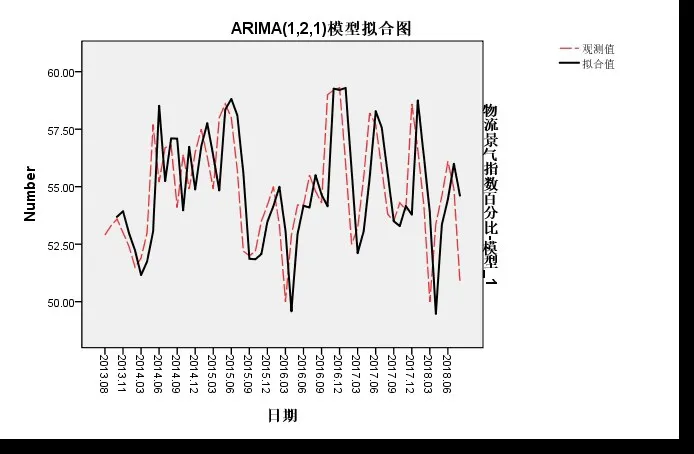
圖11 通過ARIMA(1,2,1)模型擬合數據圖
由圖11可知,利用ARIMA(1,2,1)模型進行原始序列的擬合幾乎一致波動,擬合精確度比灰色GM(1,1)預測和BP神經網絡預測要高很多,預測誤差大大縮小。
通過ARIMA(1,2,1)模型預測2018年8月到2018年12月的物流景氣指數,見表4。

表4 未來五期LPI預測值
3.3.3 預測結果分析。通過ARIMA(1,2,1)模型預測結果可以看出,物流景氣指數將會走出先前小波回落期,2018年未來幾期物流景氣指數將呈現上升趨勢,物流活動將繼續呈現活躍狀態,且物流景氣指數預測值將會在2018年11月份出現全年峰值。從誤差分析也可進一步看出,由ARIMA模型預測物流景氣指數精度最高,預測值和真實值擬合度也比之前兩種預測要好。
4 結論分析
伴隨著云計算、物聯網等信息技術的成熟以及“一帶一路戰略”、“互聯網+物流”、“十三五計劃”等政策實施,將會加速物流業的發展,物流活動逐漸成為社會各項活動的重要基礎,在社會活動中扮演著重要角色。現代物流業作為國民經濟的基礎性產業,融入了運輸業、倉儲業和信息業等多個產業,它的發展不僅與各個企業運營緊密聯系,而且牽動著一國經濟的運行和發展。通過物流景氣指數(LPI)呈現我國物流發展趨勢的同時反映出我國經濟發展情況,是我國經濟運行趨勢的晴雨表,對指導企業生產運營和投資等活動具有一定的參考價值。物流景氣指數的上升,清晰地反映出我國物流需求回升,市場規模擴大,經濟向好的態勢,而物流景氣指數下降,在一定程度上預示著市場需求下滑,經濟趨向低迷。
本文通過統計2013年8月到2018年7月的物流景氣指數(LPI)數據,利用灰色GM(1,1)預測模型、BP神經網絡和ARIMA模型對原始數據的擬合,通過誤差和分布圖分析得到最佳預測模型,對于原始數據波動很大且無周期性存在時,使用ARIMA模型將縮小誤差提高預測精準度[8],通過差分轉換將波動數據轉為穩定數據,進行數據擬合得到與原始序列擬合度最高的差分階數d,最后進行參數估計,采用最佳的定階模型對未來幾期物流景氣指數進行預測。預測結果表明,2018年8月之后物流景氣指數將出現回升狀態,物流活動將持續活躍,且預測結果顯示在2018年10月到11月將出現年末峰值,物流景氣將呈連續增長態勢。

