熱測地場控制的近似剛性網格變形技術

邵茂真，壽華好

?

熱測地場控制的近似剛性網格變形技術

邵茂真，壽華好

(浙江工業大學理學院，浙江 杭州 310023)

為保持三維模型局部細節，修正近似剛性網格變形算法(ARAP)應用于大尺度以及非完全剛性變形中出現的扭曲、翻折問題，提出了一種基于測地場約束的近似剛性變形方法。首先對模型進行Laplacian變形，并通過奇異值分解求得局部單位的旋轉矩陣，計算模型剛性變形能量；然后通過求解稀疏線性系統，更新變形點，再通過求解兩次稀疏線性系統，計算變形過程中產生的測地場偏差，并修正變形網格，得到與原始網格測地場接近的變形結果；反復迭代上述步驟，直到熱測地場偏差滿足一定要求，獲得最終變形結果。結果表明，該方法能在網格變形過程中快速地完成網格點修正功能，在應用于大尺度變形中也能有效地避免網格出現翻折問題。

近似剛性變形；熱測地場；稀疏線性系統；翻折

隨著近年來計算機圖形學飛速發展，三維幾何模型尤其是三角網格模型在動畫、游戲、3D打印、電影等相關領域得到了廣泛應用。三角網格變形作為常用的一個幾何處理工具，能根據用戶的交互操作，對原模型進行變形，以表達用戶特定的創作 意圖。

網格變形一直是計算機圖形學中較為活躍的一個方向。本文只討論與微分域的網格變形方法相關的方法以及所用的一些思想和概念。

微分域網格變形實質上是一個用微分坐標描述網格變化的問題，其是非線性問題，因為微分坐標是非線性的依賴頂點位置。Laplacian變形[1-4]方法已經得到了廣泛的發展，可通過保持變形前后的Laplacian坐標來保持局部細節，但其變形均需對旋轉變形加入約束或定義[5]。另一種解決旋轉變換的方法，是從保持局部的剛性入手以保持局部細節，使用ARAP能量體現，在幾何處理中得到了廣泛的應用。基于此能量，SORKINE和ALEXA[3]提出了一種網格變形方法，只需要控制頂點的約束，整個變形就能自動的完成，并且局部的旋轉變換也能自動地在迭代優化中產生。該變形方法近年來在效率[6]和效果[7]上得到了發展。

ZHOU等[4]引入體積圖Laplacian算子，將三角網格內部與表面巧妙地聯系起來，使得變形后的圖形能較好地保持原有體積，同時能夠很好地避免曲面的自交。通過類似泊松變形的傳播方法將控制曲線的變換顯式地傳播到興趣區域，最后通過線性變分的方法求解變形網格。文獻[8]將該方法簡化后應用到近似剛性網格變形之中，實現了保細節以及整體近似剛性的變形。文獻[9]另辟蹊徑，以三角形與坐標原點構成的四面體的有向體積加權和表示模型體積。通過將模型的剛性保持和體積保持轉化為網格頂點位移的約束求解，實現三維物體的近剛性保體變形。

GAO等[10]用L1范數代替傳統的L2范數優化ARAP能量函數，使得扭曲處得到減少，且更好地保持幾何特征。文獻[7]將旋轉差項加入到ARAP能量函數中，實現了相對剛性旋轉的光滑處理。CHAO等[11]將1-鄰域的ARAP能量框架擴展到2鄰域上，得到了一個連續的ARAP能量框架。CHEN等[12]將此鄰域擴展為任意大小的并且內部可以存在多種鄰域結構的ARAP能量框架，實現了剛性可控的ARAP網格變形技術。

AU等[13]將等值線和剛性信息與控制點(handle)聯系起來，提出了一種控制點等值線引導的網格編輯手段與本文方法較為相似。CRAME等[14]巧妙地將熱傳播與測地距離兩者聯立起來，將熱傳播方向認為是測地距離的負梯度方向，極大地提高了求源點到網格上其他點距離所需的時間。本文認為在近似剛性的網格變形中，變形前后對于源點的測地距離標量場(測地場)應該是大致不變的，此觀點在做近似剛性變形的迭代過程中得到了佐證，同時，測地場也在不斷地逼近變形前網格測地場。

1 本文算法框架

傳統的ARAP變形技術只能保證相連頂點之間的剛性結構，這使得在變形的過程中不相連頂點之間會發生較大的拉扯從而改變原來的測地距離，如圖1所示。

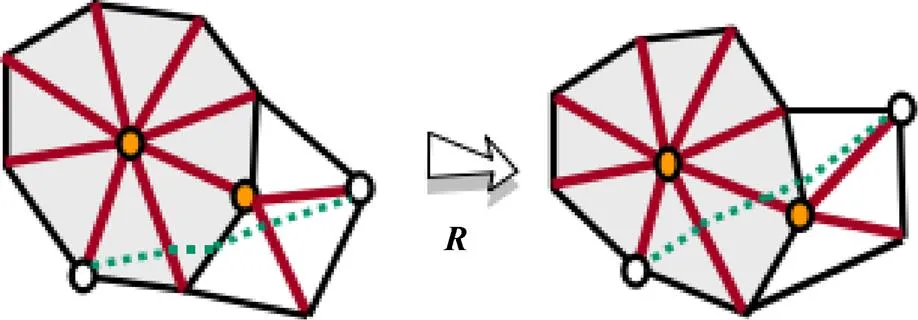
圖1 網格變形前后測地距離路徑發生改變

針對此現象，本文提出了一種測地場約束的ARAP網格變形技術。且分別采用剛性變形能量E和測地場變形能量E衡量曲面的剛性變形誤差和距離場誤差。相應地，模型的變形過程即是最小化變形能量的過程，即

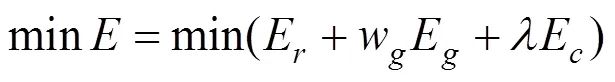
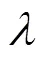
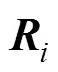
2 熱測地場控制的ARAP網格變形

2.1 ARAP網格變形技術[3]

當給定一個三角網格，其主要拓撲結構由個點和個三角形構成。()為與頂點相連的所有頂點的集合，稱為1-鄰域頂點。

ARAP變形算法定義網格頂點與1-鄰域的頂點和邊構成剛性變形單元，每個相似大小的變形單元重疊地覆蓋整個網格表面。變形的過程假設所有的變形單元只發生剛性變換，即

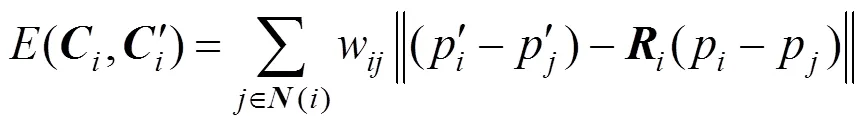
整個變形區域的能量函數是每個變形單元的能量函數之和，即

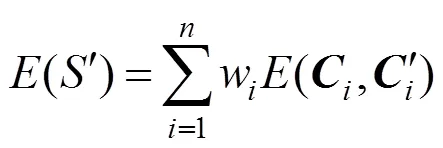
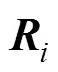
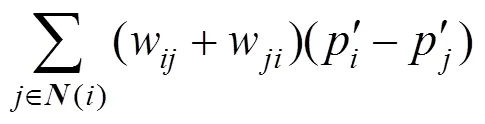
一般的網格變形就在?預定義部分約束點，其中包括靜態不變動的點與主導變形的控制點(handle vectices)，一般由用戶交互地給定

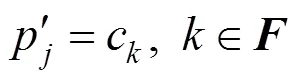
反復迭代上述的和，如此反復迭代直到能量誤差達到一定的閾值或趨于穩定為止。

2.2 熱測地場[14]

文獻[14]提出了利用熱運動方程來計算網格測地線的方法，即當一根燙的針尖接觸到曲面上的一點時，熱量會隨著時間的推移而擴散，測地距離因此可以和熱運動相聯系。

熱測地線算法步驟如下：

輸入：熱源點v。

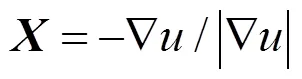
步驟3. 得到測地距離的梯度之后，測地線的問題即為

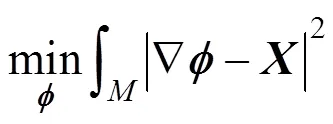
根據變分法，式(8)最小化即為求解泊松方程

應用在三角網格中時，通過離散化處理，只要求解兩次稀疏線性方程組，在時間和效率上均有較好的改進。

本文將每個頂點到熱源點測地距離構成標量場簡稱為熱測地場，如圖2所示。

本文提出假設：近似剛性網格變形前后的熱測地場也是近似不變的，在此基礎上觀察近似剛性網格變形過程中熱測地場的變化，此時變形非完全剛性的變形，發現熱測地場也以較為緩慢的速度逼近變形前網格測地場，如圖3所示。

在上述例子中近似剛性網格變形迭代5次后，近似剛性能量已經趨于不變，如果按原先的標準圖3(b)當作最終的變形結果輸出，本文對其繼續迭代并做測地場觀察發現，盡管其近似剛性能量不再變小反而會出現微微增大的情形，但其測地場能量仍在持續減小，并在迭代30次時達到收斂，此時測地場與原測地場的差異已經非常小。

圖2 標準兔子模型的熱測地場

圖3 ARAP算法測地場差異圖

(黑色圓點為變形控制點，其中橘色越深代表該處測地距離差異越大，藍色則表示該處測地距離沒有發生變化)

2.3 熱測地場控制的ARAP能量函數構造

針對上述觀察結果，本文提出了一種新的測地場控制下的近似剛性網格變形技術。

采用距離場差的和表示熱測地場變形能量

將其帶入式(1)，則原問題就變成最小化總能量函數

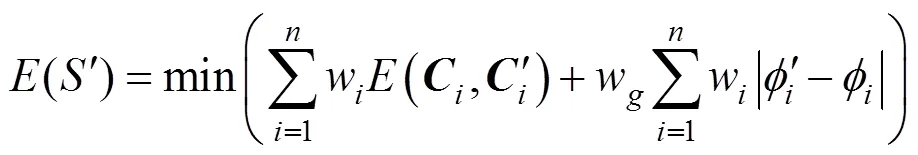
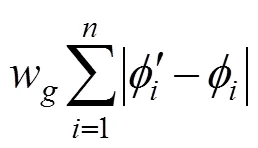
2.4 熱測地場控制的ARAP模型框架

本文在非完全剛性的變形應用ARAP網格變形技術時，其近似剛性變形能量并非向0收斂，相反會收斂于一個較大的常數。此時三角網格的邊長有很大一部分發生了伸縮變換，影響能量函數對輸出結果的一個判斷，因此采用式(11)作為新的能量函數，其中w取較大常數時，該能量函數具有收斂性，同時定義變形終止條件為

本文算法步驟如下：

輸入.起始三角網格，控制點，熱源點v。

輸出.變形后網格。

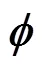
步驟2. 根據所得和式(6)更新。

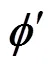
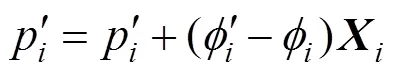
源點的選擇直接決定了其他點的測地距離，以及測地場修正過程中的導向。若選用控制變形的控制點作為源點，修正過程將在修正測地場的同時，其他參與修正的頂點也將向變形最終位置逼近，加入測地距離修正能加快變形收斂速度的原因也在于此；若選用其他參與變形的頂點，由于該頂點自身存在隨機偏差的原因，最終修正雖然能夠修復網格內部折疊現象，但會導致整體變形都加入隨機偏差，該偏差會在下次ARAP變形中修正，一個不好的源點選擇可能導致網格變形消耗更多的時間。若選用不動點作為源點，同參與變形點一樣極有可能變形減慢，增加時間 成本。

測地場約束是如何修正網格內部折疊的呢？

網格內部折疊的根本原因在于ARAP網格變形過于強調cell結構的不變性，為了能達到此效果，當發生非剛性變形或大幅度變形時，會以折疊和拉伸的方式來保證cell結構的近似不變，在此情況下ARAP的能量消耗最小。而折疊區域的另一直觀結果，就是到某一源點的測地距離場發生了極大變化，即改變了原先的測地距離分布。圖8(b) Tyra模型尾巴部分可以直觀地看到這一現象。

式(13)以前一次變形的測地場梯度方向作為修正方向，測地距離的差值作為修正值，重新定位頂點位置，不改變原拓撲結構，近似地得到與前一次測地距離場分布相同的變形結果。

3 實驗結果與分析

本文算法運行環境為：Windows 7，i5-4590CPU@3.30 GHz，4 GB。且在Visual Studio 2012上實現的，稀疏線性方程組和矩陣的奇異值分解使用的均是Eigen庫，為了加快線性方程組的求解過程，對所有方程組的求解均用了基于Cholesky分解的解法。

圖4為本文算法在測地場差異變化過程，并與圖3進行比較，還以折線圖(圖5)的方式展示了兩者的迭代收益。

本文算法以熱測地場為約束進行網格的重新排列，對每次迭代出現的畸形網格做優化處理，以保證每次迭代所得網格拓撲結構不發生變化，同時在一定程度上縮減了ARAP變形所需的時間。圖6(b)展示了在第5次ARAP變形迭代時Armadillo鼻子處出現的畸變，此時其熱測地場能量高頂點主要分布在Armadillo上部分。通過本文算法對Armadillo進行熱測地場修正，有效地消除了在鼻子處的畸變問題，同時其熱測地場也與原形狀的熱測地場趨于接近。

圖4 本文算法測地場差異圖

(黑色圓點為變形控制點，其中橘色越深代表該處測地距離變化越大，藍色則表示該處測地距離沒有發生變化)

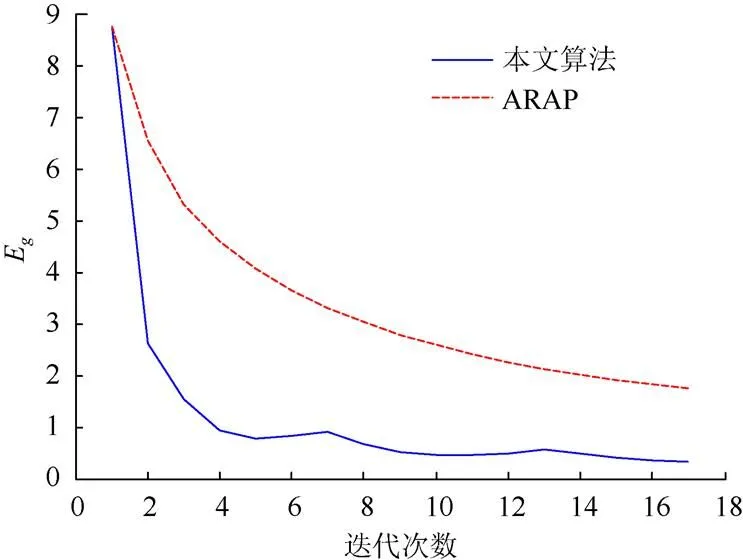
圖5 Bunny變形Eg變化對比圖

對尾巴、腳這類動畫常用變形進行觀察(圖7)，當出現大角度的非完全剛性變形時(圖中尾巴部分)，ARAP變形極其容易發生改變網格內部翻折的情形。圖7紅色框內為不參與變形網格頂點，紅色頂點為控制點，將其分別變形到藍點位置，ARAP算法和本文算法均迭代8次。可以看到圖7(b)中在尾巴位置發生了網格折疊的情形，這是由于ARAP對大尺度、非完全剛性變形的缺點。而本文算法則很好地解決了這一問題，如圖7(c)所示。圖8為Tyra尾部網格對比圖，圖9為Cactus變形對比圖。

圖6 Armadillo變形對比圖

圖7 Tyra變形網格對比圖

圖8 Tyra尾部網格對比圖

圖9 Cactus變形對比圖

在時間效率上，本文算法加入了計算測地場的步驟，但慶幸的是，計算測地場中多次所用的Laplacian算子在ARAP變形中已經計算得到，因此在一定程度上縮減了測地場計算所需的時間。在圖形效果上，加入測地場約束能有效地避免大尺度以及非剛性變形所出現的畸變情況，通過測地場能量的約束，可加速圖形的收斂速度。從表1可以看出，加入測地場優化所需要的時間僅為ARAP變形的1/3。

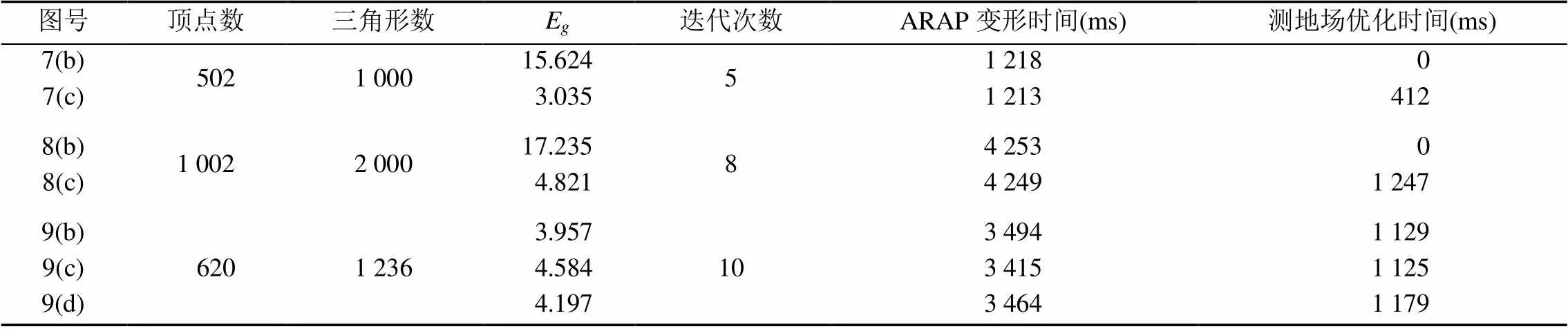
表1 本文算法運行時間

4 結束語

本文對ARAP變形技術進行拓展，加入了測地場優化這一步驟，改善了大尺度變形以及非剛性變形中出現的畸變，在保持ARAP變形技術的同時保持曲面細節，用測地場優化來實現宏觀調控，加速了網格變形。以測地場能量來衡量網格變形優劣，避免了ARAP變形技術在非完全剛性變換時，能量函數在迭代過程中出現逆增長，而影響變形評價系統對變形完成程度的衡量。

本文算法的不足之處，當網格變形改變圖形拓撲結構時，所提假設變形前后測地場變化較小將被否決；另并未將測地信息直接地加入到網格變形中，在今后的工作中需對其進行改進。

[1] YU Y Z, ZHOU K, XU D, et al. Mesh editing with poisson-based gradient field manipulation [C]//ACM SIGGRAPH. New York: ACM Press, 2004: 644-651.

[2] SORKINE O, COHEN-OR D, LIPMAN Y, et al. Laplacian surface editing [C]//In Proceeding of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing. New York: ACM Press, 2004: 175-184.

[3] SORKINE O, ALEXA M. As-rigid-as-possible surface modeling [C]//Proceedings of the 5th Eurographics Symposium on Geometry Processing. Aire-la-Ville: Eurographics Association Press, 2007: 109-116.

[4] ZHOU K, HUANG J, SNYDER J, et al. Large mesh deformation using the volumetric graph Laplacian [J]. ACM Transactions on Graphics, 2005, 24(3): 496-503.

[5] LIPMAN Y, SORKINE O, LEVIN D, et al. Linear rotation-invariant coordinates for meshes [J]. ACM Transactions on Graphics, 2005, 24(3): 479-487.

[6] SUESSMUTH J, ZOLLH?FER M, SERT E, et al. GPU based ARAP deformation using volumetric lattices [C]// Eurographics 2012. Goslar: Eurographics Association Press, 2012: 85-88.

[7] LEVI Z, GOTSMAN C. Smooth rotation enhanced as-rigid-as-possible mesh animation [J]. IEEE Transactions on Visualization and Computer Graphics, 2015, 21(2): 264-277.

[8] 杜正君, 張慧. 體積圖控制的近似剛性的網格變形[J]. 計算機輔助設計與圖形學學報, 2016, 28(2): 218-227.

[9] 劉炯宙, 李基拓, 陸國棟. 三維模型近剛性保體變形[J]. 計算機輔助設計與圖形學學報, 2013, 25(4): 533-540.

[10] GAO L, ZHANG G X, LAI Y K. Lp, shape deformation [J]. Science China Information Sciences, 2012, 55(5): 983-993.

[11] CHAO I, PINKALL U, SANAN P, et al. A simple geometric model for elastic deformations [J]. ACM Transactions on Graphics, 2010, 29(4): 157-166.

[12] CHEN S Y, GAO L, LAI Y K, et al. Rigidity controllable as-rigid-as-possible shape deformation [J]. Graphical Models, 2017, 91: 13-21.

[13] AU K C, FU H, TAI C L, et al. Handle-aware isolines for scalable shape editing [J]. ACM Transactions on Graphics, 2007, 26(3): 83.1-83.10.

[14] CRANE K, WEISCHEDEL C, WARDETZKY M. Geodesics in heat: A new approach to computing distance based on heat flow [J]. ACM Transactions on Graphics, 2013, 32(5): 13-15.

As-Rigid-As-Possible Mesh Deformation Controlled by Geometric Field in Heat

SHAO Mao-zhen, SHOU Hua-hao

(College of Science, Zhejiang University of Technology, Hangzhou Zhejiang 310023, China)

In order to maintain the details of the 3D model, correct the problem of distortion and folding of the as-rigid-as-possible (ARAP) mesh deformation used in large and nonperfect rigid deformation, an ARAP deformation method is proposed based on geometric field in heat. First, the Laplacian deformation of the model is carried out. On this basis, the rotation matrix of local cell is solved by singular value decomposition, and the rigid deformation energy of the model is calculated. Then by solving the sparse linear system, the deformation points are updated. By solving the two-time sparse linear system, we calculate the geometric field deviation of the deformation process, and correct the deformed mesh to get the deformation results close to those of the original mesh. Iterate the above steps until the geometric field deviation to meet certain requirements, and finally the final deformation results are obtained. The example shows that the method can quickly complete the mesh point correction function in mesh deformation process, and it can also effectively avoid grid collapse when applied to large-scale deformation.

as-rigid-as-possible mesh deformation; geometric field in heat; sparse linear system; folding

TP 391

10.11996/JG.j.2095-302X.2019010001

A

2095-302X(2019)01-0001-07

2018-06-26；

2018-07-13

國家自然科學基金項目(61572430)

邵茂真(1994-)，男，浙江金華人，碩士研究生。主要研究方向為可視化計算。E-mail：434850246@qq.com

壽華好(1964-)，男，浙江諸暨人，教授，博士，碩士生導師。主要研究方向為計算機輔助幾何設計與圖形學。E-mail：shh@zjut.edu.cn