基于多結點樣條磨光函數的幾何迭代法

霍彥妏，蔡占川

?

基于多結點樣條磨光函數的幾何迭代法

霍彥妏，蔡占川

(澳門科技大學資訊科技學院，澳門 999078)

幾何迭代法在計算機輔助幾何設計(CAGD)中有廣泛地應用，為了提高傳統的B-樣條曲線插值在幾何迭代中的收斂速度和迭代精度，提出了基于多結點樣條磨光函數的幾何迭代法，引入多結點樣條磨光函數，在曲線擬合時把多結點樣條磨光方法和幾何迭代方法結合，經過磨光和迭代，在L-BFGS迭代算法的最優解下構造具有高逼近性的曲線擬合方法。實驗結果表明，在相同精度下，該方法不僅減少了迭代次數，且提高了迭代速度，可以用于飛機、汽車等外形設計上，亦可用于文物、房屋等外形重構和重建，以及衛星圖形圖像的處理中。

幾何迭代法；多結點樣條磨光；L-BFGS算法；B-樣條

1 研究背景

幾何迭代法[1-2](geometric iteration method，GIM)，早期被稱為漸進迭代逼近(progressive- iterative approximation，PIA)，其是迭代逼近算法在幾何設計中的應用。該方法是將原始的離散數據點集用迭代的方法調整控制點，形成逐漸逼近控制點的新樣條函數，最終形成一條光滑且具有更高逼近性的曲線或曲面的一種圖形數據擬合方法[3]。

幾何迭代法在計算機輔助幾何設計(computer- aided geometric design，CAGD)中，解決的主要問題是工業產品幾何形狀的數字描述，例如汽車車輪、渦輪發動機、飛機外形的設計。CAGD技術起源于航空工業，由于飛機外形流線型的特殊結構是由多個自由的曲線及曲面組成的，所以CAGD技術的研究與曲線、曲面的發展息息相關。

1975年，齊東旭等[4]提出均勻三次B-樣條的盈虧修正曲線擬合數值磨光方法，之后又在文獻[5-6]中提出多結點樣條的磨光方法，即用高階的多結點樣條磨光來達到更高的逼近效果，使“盈虧修正”方法得到更好地拓展和延伸。DE BOOR[7]于1979年也研究盈虧修正并且證明了該方法的收斂速度。2004年，LIN等[8]在非均勻三次B-樣條的研究上證明了其同樣具有盈虧修正的性質，隨后在2006年提出了漸進迭代逼近(progressive iterative approximation，PIA)[9-13]的概念，并證明了幾何迭代的性質同樣適用于歸一化的全正基混合曲線和曲面中。

2007年DELGADO和PE?A[14]對比了在迭代過程中當取不同基函數的樣條函數時，各自的收斂速度不同，且證明了B-樣條的基函數迭代具有最高的收斂速度。同年，MAEKAWA等[15]用相鄰數據點的參數值代替原始點的參數值并提出了幾何插值(geometric interpolation，GI[16])的概念。熟知，由于PIA和GI[17]方法的相似性，在CAGD研究領域，被統稱為幾何迭代法。

為了提高函數的迭代精度以及收斂性，本文提出基于多結點樣條磨光函數方法的幾何迭代法，采用L-BFGS算法求型值點和調整后控制點之間距離的最小值即最優解，選取最恰當的點，以得到更加光滑且更加逼近型值點的幾何圖形。實驗結果表明，該方法在相同的精度下，比通用的三次B-樣條曲線插值迭代次數減少，且收斂速度成倍加快，不僅有效地保證了幾何外形的精確性，還保持了其光滑的特性。

2 相關工作(GIM基本思想)

按此規律，生成的樣條曲線的表達式如下：經過+1次迭代后，向量的差值為

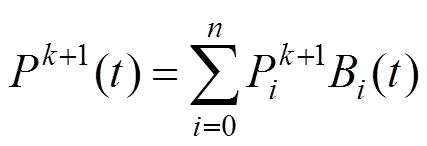
圖1 迭代示意圖

3 多結點樣條磨光函數

自由曲線或曲面的數據擬合是幾何圖形設計中不可或缺的部分。為了提高三次B-樣條曲線或曲面的收斂性以及精確性，本文探討多結點樣條磨光方法并研究其迭代的幾何意義。

當前，在CAD/CAM系統中，B-樣條曲線曲面已經發展為被廣泛使用、很成熟的一類樣條方法。在齊東旭等[4]提出均勻的三次B-樣條曲線擬合數值磨光方法；之后，為了推廣B-樣條函數，在保證樣條曲線的精確性和光滑性同時兼顧的情況下，又引入級磨光算子，推出了“多結點” B-樣條函數的磨光法[5-6]。事實上，B-樣條函數是將次數為0的磨光算子在寬度=1的情況下，不斷地磨光計算得出的函數[5]。

在研究曲線或曲面的擬合逼近問題時，齊東旭[18]研究了單位算子，并推出含有微分算子的樣條函數磨光公式，使微分算子的逼近運算精度更高[19]。文獻[20]研究了層次多結點樣條算法曲線曲面的擬合和應用。

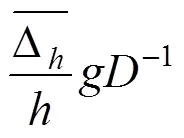
多結點樣條磨光函數的定義為

圖2 邊界延拓示意圖

樣條函數的次數可以有0次，1次，2次， 3次······，由次數分別為0，1，2，3的表達式形成的基函數的圖像，如圖3所示。

多結點樣條磨光法的優點：

(1) 一般性。該磨光方法只儲存型值點，即不論幾何圖形是貓、狗亦或是松鼠這類型值點個數不同的幾何圖形，但其應用曲線的表達式都是統一的，在處理結果的誤差上相比常用到的最小二乘法更小。

(2) 整體性。不論型值點如何增加，迭代的次數如何改變，幾何圖形的形狀均能保持和基本初始的數據形狀一致。

(3) 局部性。改變個別的數據點后，只會隨之影響這些點對應的個別部分，而整體的幾何圖形形狀不會改變。

圖3 K=0,1,2,3時多結點樣條基函數圖像

4 基于多結點樣條磨光函數的幾何迭代法

熟知，牛頓法在進行Hessian的逆運算時，不僅費時而且占用大量內存空間，給計算帶來很大的不便。相比牛頓法，BFGS算法由于Hessian的正定性即參數化的數據點唯一有且只對應一個數據點，并不需要求解Hessian，也就不需要占用很大的內存空間來存儲每次生成的矩陣結果，既節省存儲空間又提高了運行速度。而L-BFGS算法更是被稱為“節省內存的BFGS算法”。

1989年LIU和NOCEDAL[21]提出了L-BFGS (Limited-memory BFGS)算法，該算法常應用于規模較大的數據處理的數值計算中。

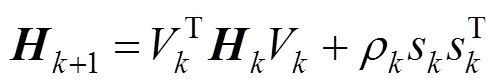
其中，

上式是=3的情況，由于實驗研究的是三次多結點樣條磨光的基函數，所以其他3種情況的表達式不做說明。

在使用均勻三次B-樣條函數進行數據擬合時，需求解一組線性方程的根來確定該幾何形狀控制頂點的位置。反向求解方式為確定樣條函數的系數帶來了很大的不便，既增大運算量，又延長了運算時間。本文采用多結點樣條磨光方法來克服B-樣條函數的不足。由圖4可知，使用三次多結點樣條磨光函數和三次B-樣條函數做對比，多結點樣條磨光函數的逼近效果要好于B-樣條函數，提高了幾何輪廓的精確性，而且更加逼近原始型值點。

圖4 多結點樣條磨光函數與B-樣條對比

基于多結點樣條磨光函數幾何迭代方法算法如下：

輸出：找到最小化函數值對應的坐標、步長、梯度、精度。

步驟1. 初始化階段，選擇起始結點，原始型值點參數化。

步驟2. 形成初始磨光樣條函數曲線。

步驟3. 迭代次數=1；

步驟3.1. 閾值判定；

步驟3.2. 迭代正向或逆向求解。

步驟4. 閾值判定；

步驟4.1.若符合條件，畫出曲線；

步驟4.2. 若不符合，=+1，循環步驟3，4。

本文算法流程圖如圖5所示。

5 實 驗

本文的實驗操作是基于16 G內存，i7-6700 CPUintel (R)處理器，在MATLAB編譯器上完成本文的實驗內容。

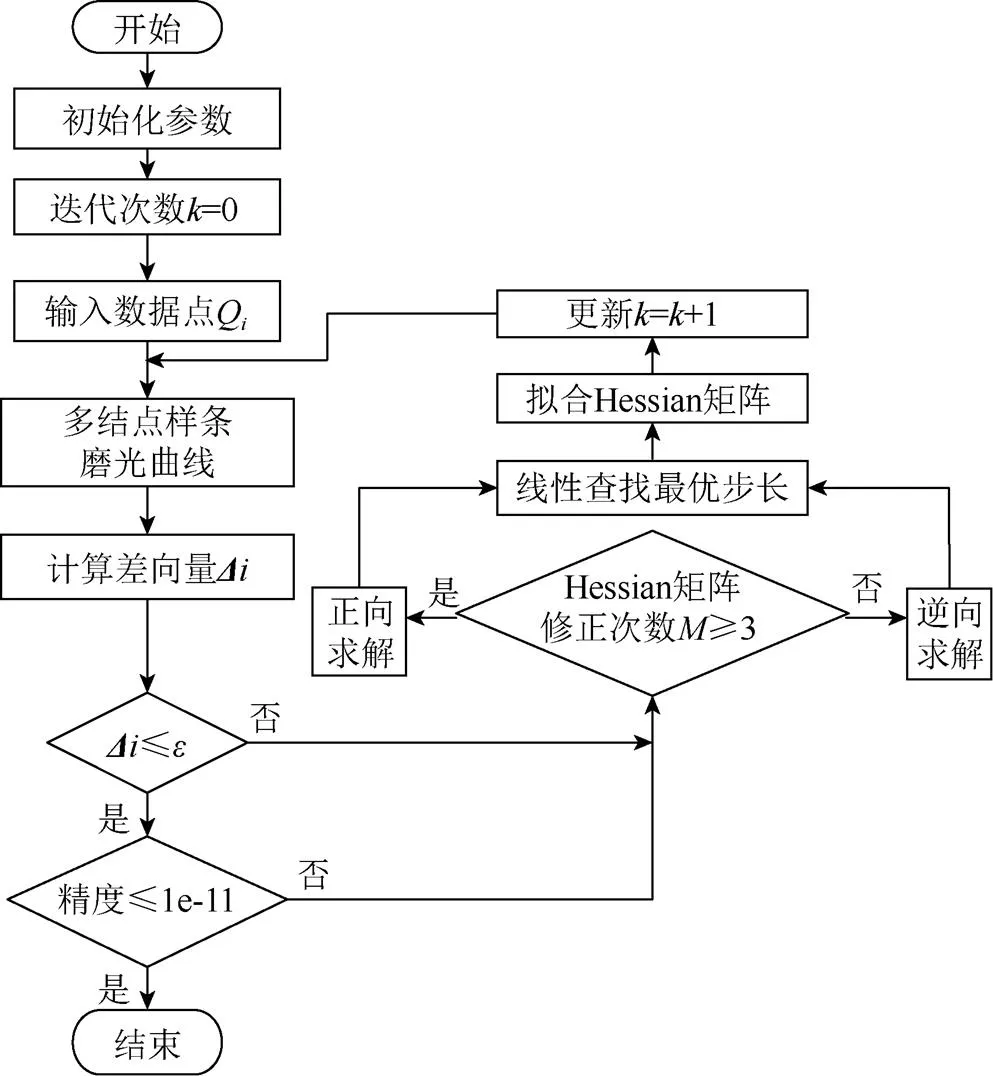
圖5 本文實現過程流程圖

5.1 實驗結果

研究幾何迭代法離不開研究擬合曲線迭代的速度和精度，即算法收斂性。文獻[28]中在三次B-樣條函數的基礎上對各種幾何圖形做出了相應的迭代擬合。圖6~20是本文算法與文獻[28]的實驗結果的對比圖。當原始型值點個數不同且接近100個數據點時，最大的迭代次數在5次以內就可以達到所需的精度值。為了驗證本文算法的收斂性，通過以下5種實例來驗證算法的迭代效果以及精度分別與迭代次數和時間的關系。

在精度與迭代次數和時間的對比關系圖中，顯示相同的精度設置下的對比結果，藍色線條為三次B-樣條函數方法實現的迭代結果，紅色線條為多結點樣條磨光函數方法實現的迭代實驗結果。由圖6~20可知，在相同精度下，多結點樣條磨光函數方法可比三次B-樣條用更少的迭代次數和運行時間更加迅速地達到閾值條件。

5.2 實驗分析

由表1和圖21不同幾何圖形的精度對比以及表2的5種迭代詳細情況對比可知，5種不同的幾何圖形用本文的算法迭代后在5次之內均可達到閾值迭代精度。

圖6 牛迭代實驗結果

圖7 牛誤差與迭代次數關系

圖8 牛誤差與時間關系

圖9 松鼠迭代實驗結果

圖10 松鼠誤差與迭代次數關系

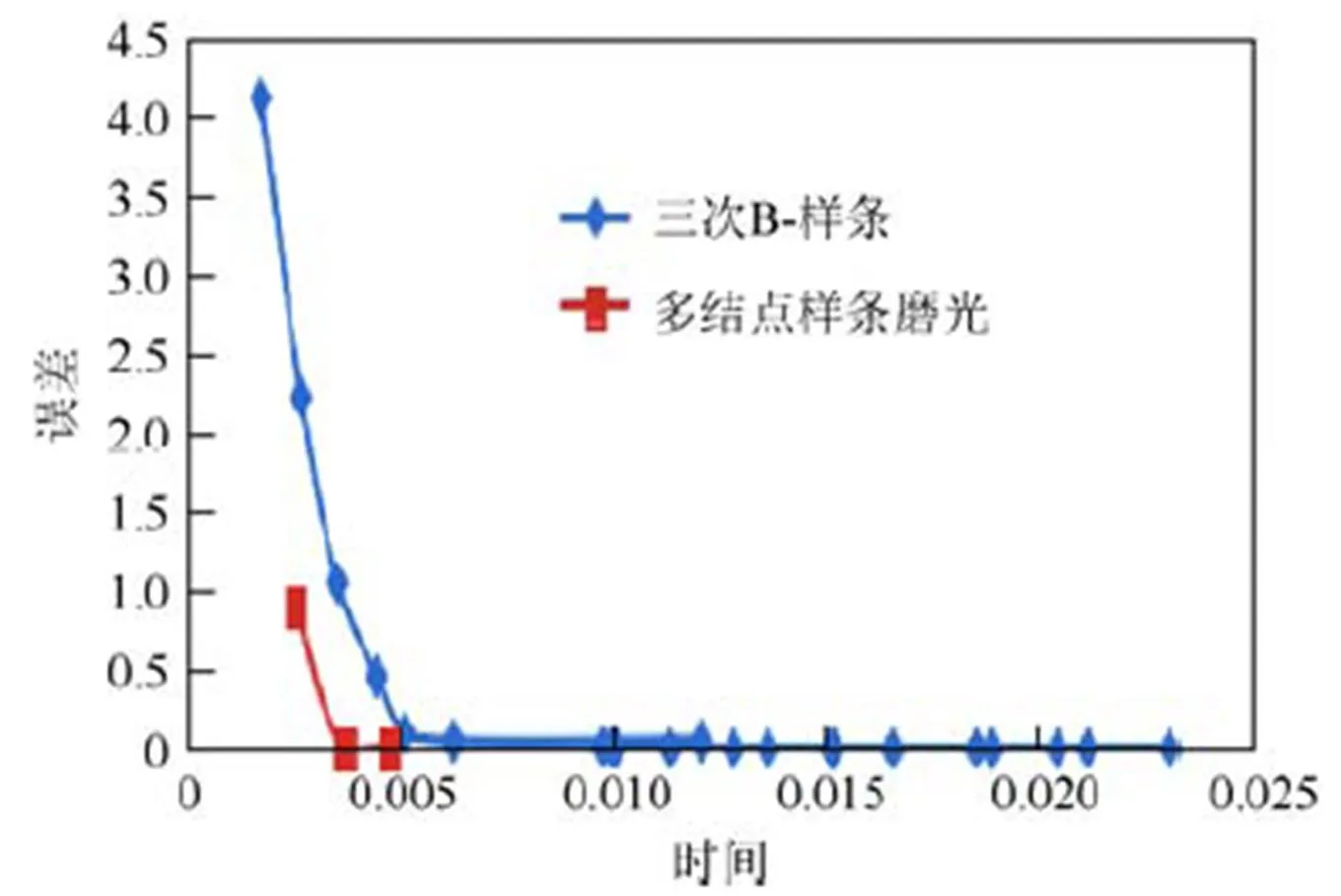
圖11 松鼠誤差與時間關系

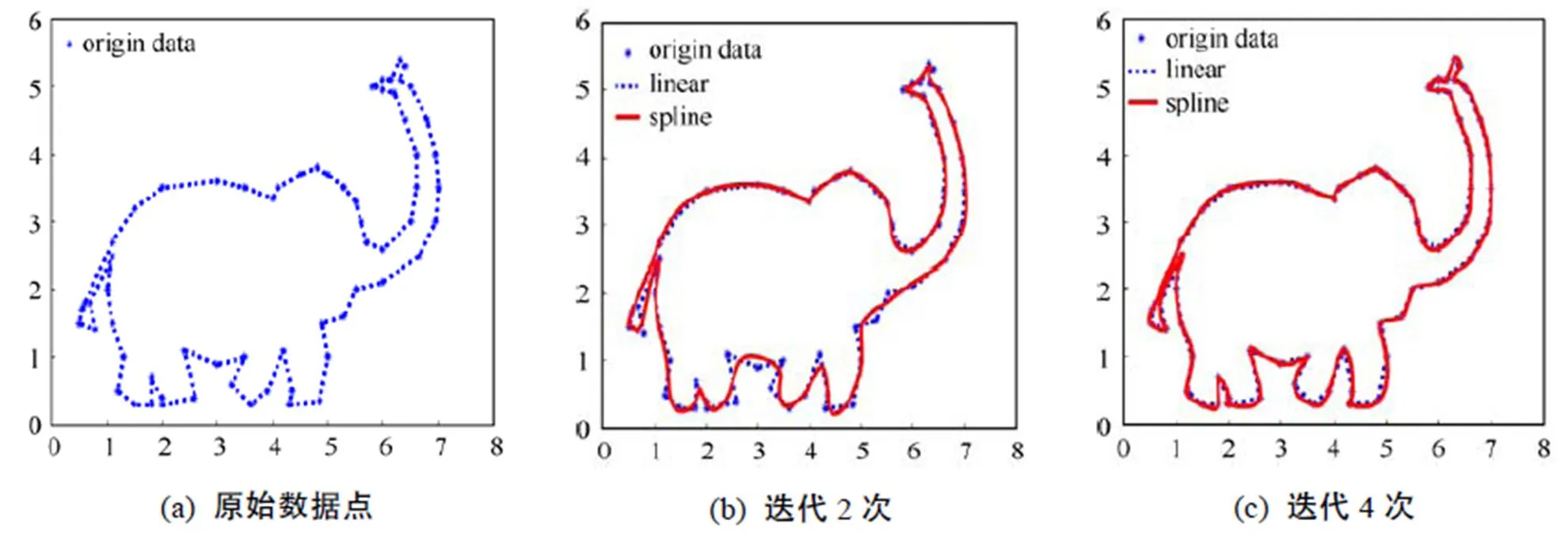
圖12 大象迭代實驗結果

圖13 象誤差與迭代次數關系

圖14 象誤差與時間關系

圖15 米老鼠迭代實驗結果

圖16 米老鼠誤差與迭代次數關系

圖17 米老鼠誤差與時間關系

圖18 螃蟹迭代實驗結果

圖19 螃蟹誤差與迭代次數關系

圖20 螃蟹誤差與時間關系

表1 不同幾何圖形誤差對比

圖21 5種幾何圖像誤差對比

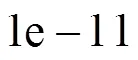
表2 采用多結點樣條磨光方法與三次B-樣條函數方法的幾何圖形迭代詳細情況對比

6 結 論

本文基于多結點樣條磨光函數，提出了相應的優化幾何迭代方法。在獲取幾何圖形的原始型值點后，利用多結點樣條磨光函數的高逼近性和局部性，采用L-BFGS算法尋找最佳迭代逼近數據點的位置，通過數次磨光和迭代產生數據的最優解，在迭代達到指定精度值后，得到所需具有“較高精確性”的光滑曲線。實驗結果表明，本文提出的磨光方法，比三次B-樣條函數曲線在幾何迭代的曲線擬合上逼近性更高，收斂性更快，在精度和速度上都有所提升。

今后，將繼續探討基于多結點樣條磨光函數的幾何迭代方法在三維的立體幾何圖形以及曲面中的應用。

[1] OKANIWA S, NASRI A, LIN H, et al. Uniform B-spline curve interpolation with prescribed tangent and curvature vectors [J]. IEEE transactions on visualization and computer graphics, 2012, 18(9): 1474-1487.

[2] LIN H, MAEKAWA T, DENG C. Survey on geometric iterative methods and their applications [J]. Computer-Aided Design, 2018, 95: 40-51.

[3] LIN H, ZHANG Z. An efficient method for fitting large data sets using T-splines [J]. SIAM Journal on Scientific Computing, 2013, 35(6): A3052-A3068.

[4] 齊東旭, 田自賢, 張玉心, 等. 曲線擬合的數值磨光方法[J]. 數學學報, 1975, 18(3): 173-184.

[5] 齊東旭, 梁振珊. 多結點樣條磨光(Ⅰ)[J]. 高等學校計算數學學報, 1979, (2): 196-209.

[6] 齊東旭, 梁振珊. 多結點樣條磨光(Ⅱ)[J]. 高等學校計算數學學報, 1981, (1): 68-81.

[7] DE BOOR C. How does Agee’s smoothing method work? [R]. Washington D C: Army Research Office 79-3, 1979: 299-302.

[8] LIN H W, WANG G J, DONG C S. Constructing iterative non-uniform B-spline curve and surface to fit data points [J]. Science in China: Series F, 2004, 47(3): 315-331.

[9] LIN H W, BAO H J, WANG G J. Totally positive bases and progressive iteration approximation [J]. Computers and Mathematics with Applications, 2005, 50(3-4): 575-586.

[10] LIN H, WANG G, DONG C. Constructing iterative non-uniform B-spline curve and surface to fit data points [J]. Science in China Series: Information Sciences, 2004, 47(3): 315-331.

[11] 鄧少輝, 汪國昭. 漸進迭代逼近方法的數值分析[J]. 計算輔助設計與圖形學學報, 2012, 24(7): 879-884.

[12] LIU M, LI B, GUO Q, et al. Progressive iterative approximation for regularized least square bivariate B-spline surface fitting [J]. Journal of Computational and Applied Mathematics, 2018, 327: 175-187.

[13] DENG C Y, LIN H W. Progressive and iterative approximation for least squares B-spline curve and surface fitting [J]. Computer-Aided Design, 2014, 47: 32-44.

[14] DELGADO J, PE?A J M. Progressive iterative approximation and bases with the fastest convergence rates [J]. Computer Aided Geometric Design, 2007, 24(1): 10-18.

[15] MAEKAWA T, MATSUMOTO Y, NAMIKI K. Interpolation by geometric algorithm [J]. Computer-Aided Design, 2007, 39(4): 313-323.

[16] LIN H. The convergence of the geometric interpolation algorithm [J]. Computer-Aided Design, 2010, 42(6): 505-508.

[17] XIONG Y, LI G, MAO A. Convergence analysis for B-spline geometric interpolation [J]. Computers & Graphics, 2012, 36(7): 884-891.

[18] 齊東旭. 關于計算機輔助幾何造型數學方法的若干注記[J]. 北方工業大學學報, 1991, 3(1): 1-8.

[19] 李岳生, 齊東旭. 樣條函數方法[M]. 北京: 科學出版社, 1979: 148-176.

[20] CAI Z C, LAN T, ZHENG C. Hierarchical MK splines: Algorithm and applications to data fitting [J]. IEEE Transactions on Multimedia, 2017, 19(5): 921-934.

[21] LIU D C, NOCEDAL J. On the limited memory BFGS method for large scale optimization [J]. Mathematical Programming, 1989, 45(1): 503-528.

[22] QIN Z W. The relationships between CG, BFGS, and two limited-memory algorithms [J]. Furman University Electronic Journal of Undergraduate Mathematics, 2016, 12(1): 5-20.

[23] NASH S G, NOCEDAL J. A numerical study of the limited memory BFGS method and the truncated- newton method for large scale optimization [J]. SIAM Journal on Optimization, 1991, 1(3): 358-372.

[24] SHANNO D F. On the convergence of a new conjugate gradient algorithm [J]. SIAM Journal on Numerical Analysis, 1978, 15(6): 1247-1257.

[25] LIU Y, WANG W P, LéVY B, et al. On centroidal voronoi tessellation-energy smoothness and fast computation [J]. ACM Transactions on Graphics, 2009, 28(4): 1-17.

[26] WANG Y C, DONG L, XUE X, et al. On the design of constant modulus sequences with low correlation sidelobes levels [J]. IEEE Communications Letters, 2012, 16(4): 462-465.

[27] WANG Y C, WANG X, LIU H, et al. On the design of constant modulus probing signals for MIMO radar [J]. IEEE Transactions on Signal Processing, 2012, 60(8): 4432-4438.

[28] 劉超, 辛士慶, 舒振宇, 等. 幾何迭代法的加速[J]. 計算機輔助設計與圖形學學報, 2016, 28(11): 1838-1843.

Geometric Iteration Method Based on Many-Knot Spline Polishing Functions

HUO Yan-wen, CAI Zhan-chuan

(Faculty of Information Technology, Macau University of Science and Technology, Macau 999078, China)

Geometric iteration method has been widely used in computer aided geometric design (CAGD). In order to improve the convergence speed and iterative accuracy of the traditional B-spline curve interpolation in geometric iterations, this study proposes the geometric iteration method based on many-knot spline polishing functions, which introduces many-knot spline polishing functions, and combines many-knot spline polishing functions method and geometric iteration method in curve fitting. After polishing operator and iterating, the curve fitting method with high approximation under the optimal solution of L-BFGS iterative algorithm is constructed. Experimental results show that the proposed method not only reduces the times of iterations, but also improves the iterative speed under the same accuracy. The proposed geometric iteration method can be used in the shape design of airplanes, automobiles, etc. It can also be used to reconstruct and rebuild the shape of cultural relic houses and satellite image processing.

geometric iteration method; many-knot spline polishing functions; limited-memory BFGS algorithm; B-splines

TP 391

10.11996/JG.j.2095-302X.2019010015

A

2095-302X(2019)01-0015-09

2018-07-02；

2018-07-21

國家基礎研究計劃“973”項目(2011CB302400)；澳門科技發展基金項目(048/2016/A2，0012/2018/A1，0069/2018/A2)；國家自然科學基金面上項目(61272364)；浙江大學CAD&CG國家重點實驗室開放課題(A1910)；北京理工大學珠海學院科研發展基金項目(XK-2018-04)

霍彥妏(1992-)，女，山西太原人，碩士。主要研究方向為計算機圖形學等。E-mail：huohyw@163.com

蔡占川(1973-)，男，河北館陶人，教授，博士，博士生導師。主要研究方向為計算機圖形圖像處理、數值分析。E-mail：zccai@must.edu.mo