多光譜生物發光斷層成像的光源形狀重建

2019-03-02 03:20:00余景景相文彬

西北大學學報(自然科學版) 2019年1期

余景景，相文彬

(陜西師范大學物理與信息技術學院,陜西西安 710119)

生物發光斷層成像(bioluminescence tomography,BLT)是一種非侵入式的,無電離輻射的光學分子影像技術。結合基因工程,使靶細胞表達出熒光素酶,熒光素酶與熒光素底物相結合,釋放出近紅外光。通過采集生物體表面的近紅外光強度分布,BLT可反演出生物體內靶細胞的能量密度的空間分布信息[1-3],從而為定性、定量地分析細胞的生理活動與新陳代謝服務。因此,BLT在癌癥的早期篩查和新型藥物的研發方面具有廣泛的應用前景[4-5]。

近紅外光在生物體內要經歷復雜的吸收、散射等過程,輻射傳輸方程(radiation transfer equation, RTE)能夠描述光在生物體內的傳輸,但由于RTE計算復雜,求解困難,所以，在實際應用中一般采用RTE的近似形式。其中,RTE的一階近似模型——擴散近似(diffusion approximation, DA)是目前應用最為廣泛的光傳輸模型[6-8]。但是，由于DA模型僅適用于散射為主的介質,因此，基于DA模型的光源重建難免存在較大的模型誤差。為平衡模型的精度和效率,研究者們還探索了各種RTE的高階近似模型,包括簡化球諧近似(simplified spherical harmonics equations,SPN)、離散坐標(discrete ordinates,SN)近似和球諧近似(spherical harmonics,PN)等,其中SPN相對效率更高[9]。對于簡化球諧近似模型,Yang等人研究表明SP3比DA有著更高的準確度和更為廣泛的應用空間[10]。Lu等人在勻質模型上進行了基于SP3的BLT重建,初步展示了SP3模型的優越性[11]。金晨等人探索了各階次SPN模型的準確性,基于SP3模型提出了變量分離近似稀疏重構的重建方法,提高了重建精度[12]。近年來,光學分子影像在其他領域的研究也表明，結合SP3模型的重建方法可以提高光源或靶目標中心的定位精度[13-14]。

近年來BLT重建的研究致力于進一步提高光源重建的精度或穩定性。這些方法的研究重點在于增加先驗信息和優化重建算法，以克服BLT重建問題的高不適定性,例如Liu等人結合多光譜測量數據和水平集策略,提高重建光源對噪聲的魯棒性[15]。Yu等人提出了基于L1/2正則化的非凸稀疏重建算法，進一步提高重建圖像質量[16]。但是，目前多數BLT重建方法都側重于定量評估光源中心位置和能量偏差,對于光源形狀的擬合關注較少[17]。實際上,光源形狀也是關鍵信息,例如在BLT引導放療應用中,重建的光源形狀與靶細胞的大小和體積相對應,對于三維適形放療有重要意義。Gao等人基于RTE前向模型和多級自適應有限元方法,結合TV范數和L1范數正則化進行重建,在二維仿真實驗中對于不同形狀的光源獲得了較好的重建結果[18],但還沒見三維成像結果的相關報告。

本文探索了BLT中的光源形狀重建問題,為進一步提高光源重建質量及形狀擬合程度,采用SP3傳輸模型減少模型誤差,運用L1范數正則化和多光譜測量數據克服BLT逆問題的不適定性，其中，重點是研究光傳輸模型對光源形狀擬合的影響,因此,實驗中著重與基于擴散方程的重建方法進行了對比,除了對重建圖像的視覺評價外,本文采用重建光源與真實光源交疊部分的體積與重建光源總體積之比,定量評價光源形狀重建的優劣。

1 理論方法

RTE的三階簡化球諧近似模型可表示為[9]

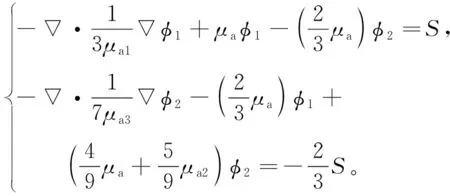
(1)

其中，μai=μa+(1-g)iμs,μa為生物組織的吸收系數,μs為生物組織的散射系數,g為各向異性系數，S是光源項,代表內部光源的能量密度分布，φi為輻射度的勒讓德矩的線性組合。SP3相應的Robin邊界條件為[9]

(2)

其中，n為方向向外的法向量,A1,B1,C1,D1,A2,B2,C2,D2是常數,由文獻[9]給出。

結合有限元(finite element method,FEM)方法,將SP3方程及其邊界條件轉化為線性矩陣方程的形式[19]，

(3)

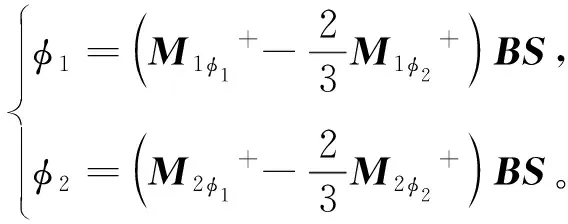
(4)

其中，Miφi+是M矩陣求逆后Miφi對應的分塊子矩陣。生物體的邊界光流量和內部光源密度的線性關系可以表示為[19]

J+=β1φ1+β2φ2。

(5)

其中，β1,β2是常數[19]。由于在BLT實驗中,只能采集到逸出生物體表面的近紅外光。除去矩陣中不可測量的部分,可得到表面能量分布和光源能量密度之間的線性關系，

(6)

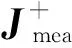
當采用多光譜測量值時,波長為λ的近紅外光與內部光源之間的線性關系可以表示為

(7)

其中，A(λi)代表不同波長近紅外光的系數矩陣,η(λi)是不同波長相關頻譜的權重[20]。為了避免測量值由單個波長的光主導,采用文獻[21]的方法進行歸一化，對每個波長的測量值除以該波長的最大測量值，為保證等式兩邊成立,對等式右邊的系數矩陣也作相應處理。可得

(8)

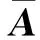
為了克服BLT問題固有的不適定性,需要通過正則化技術在重建中結合盡可能多的先驗信息,例如早期常用的各種L2范數正則化方法,以及近些年廣泛采用的稀疏正則化方法。本文結合BLT應用中光源分布的稀疏特性,采用L1正則化的方法求解式(8),將式(8)轉化為

(9)

其中，τ是正則化參數。

對于式(9)的L1范數最小化問題,已經有眾多的求解方法,如迭代收縮閾值(iterative shrinkage and thresholding,IST)算法[22]、變量分離近似稀疏重構(sparse reconstruction by separable approximation,SpaRSA)算法[23]、不完全變量截斷共軛梯度(incomplete variables truncated conjugate gradient,IVTCG)算法[24]等。

本文的重點是探討不同的光傳輸模型對形狀重建的影響,同時，由于IVTCG算法的穩定性和高效性,更重要的是,它已經得到了光學分子影像領域的廣泛應用,證實了它的穩定性和有效性[24-25],因此，我們選擇用IVTCG算法求解式(9),在下文中，將兩種重建方法簡記為DA+IVTCG和SP3+IVTCG。

2 實驗與結果

為了較為系統地評估兩種方法，在非勻質數字鼠模型Digimouse[26]上設計了一系列的單、雙光源仿真實驗,對比了多種光源設置下兩種方法的重建結果。實驗中,光源均設置在軀干部分,因此僅截取了該數字鼠模型長為40mm的軀干部分,包括心、胃、肝、腎、肺5種器官還有肌肉組織。為了模擬多光譜測量數據,采用波長分別為670nm，690nm和710nm的單色光。用于計算前向數字鼠表面測量值的光學參數如表1所示[27]。下面的實驗中,前向網格隨光源設置得略有不同,節點數均在12 000～13 000,同時，為了公平比較,所有重建采用同一個后向網格,后向網格包含6 038個節點和32 880個四面體。

為了評價實驗得出的結果,本文采用的量化指標分別為,實際光源中心點到重建光源中心的距離(location error,LE)、重建光源的平均能量密度(density),以及真實光源與重建光源的交疊體積和重建光源總體積之比(ratio between the overlapping and total volume,OVTVR)[28]。其中,OVTVR是用來定量評價重建光源形狀優劣的指標。

2.1 單光源仿真實驗

分別在低散射高吸收介質(肝)和高散射低吸收介質(肺)中設計了兩組單光源重建實驗。實驗使用了3種尺寸的光源,分別是小光源(r=0.5mm,h=1mm)、中光源(r=1mm,h=1mm)和大光源(r=1mm,h=2mm)，其中r代表真實光源的底面半徑,h代表真實光源的高。

第一組實驗是重建低散射高吸收介質(肝)中的單光源,為了研究光源尺寸和深度對重建結果的影響,將單個不同尺寸的光源放置在肝臟的不同位置處,以獲得不同的光源深度。具體地,光源中心位置分別為(14,8,16.6)mm,(14,10.5,16.6)mm和(14,12,16.6)mm,其中，距離數字鼠表面最深的光源位置為(14,12，16.6)mm,相對數字鼠背部表面深度為9mm,相對數字鼠腹部表面深度為9mm,最淺的光源位置為(14,8，16.6)mm,相對數字鼠背部表面深度為13mm,相對數字鼠腹部表面深度為5mm。真實光源的能量密度均為1nW/mm3。

圖1展示了第一組實驗中,DA+IVTCG和SP3+IVTCG對于中心位置為(14,8，16.6)mm處的不同尺寸光源的3D重建結果。重建光源定義為大于重建最大能量密度的10%的四面體,表2為重建結果的各定量指標的值。由圖1以及表2可以看出,SP3+IVTCG不僅在光源中心定位和重建能量密度上優于DA+IVTCG,OVTVR也是DA+IVTCG的1.96～3.12倍。

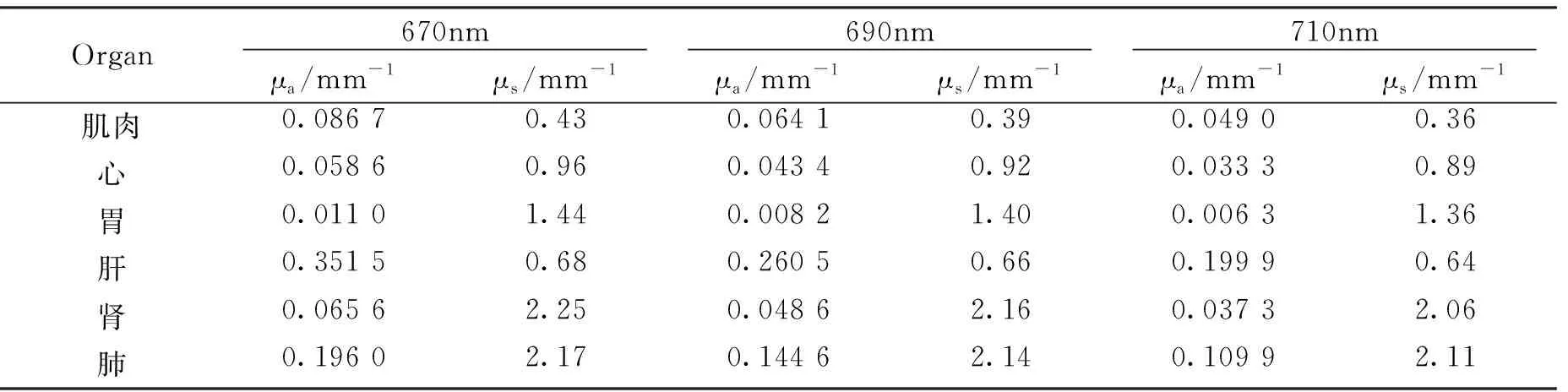
表1 數字鼠各器官的光學參數[27]Tab.1 Optical parameters of various organs at different wavelengths in digital mouse

圖1 DA+IVTCG和SP3+IVTCG對中心位于(14,8，16.6)mm處的不同尺寸單光源的重建結果。(a)～(c)是DA+IVTCG的重建結果在真實光源中心z=16.6mm處的截面視圖,其中黑色圓圈為真實光源位置。(d)～(f)是SP3+IVTCG對應的重建結果。Fig.1 The reconstruction results of different single sources centered at (14,8，16.6)mm by DA+IVTCG and SP3+IVTCG.(a)～(c) are the section views at z=16.6mm of the reconstruction results by DA+IVTCG, where the black circles denote the real light sources.(d)～(f) are the corresponding reconstruction results by SP3+IVTCG.

圖2和圖3分別為第一組實驗中光源的中心位置在(14,10.5，16.6)mm和(14,12，16.6)mm處的重建結果,圖2,圖3的結果也和圖1一致,以及由表2也可以看出,SP3+IVTCG的重建光源在形狀、定位誤差、以及平均能量密度上均優于DA+IVTCG。尤其對(14,12，16.6)mm處的光源優勢更明顯,OVTVR在小光源重建時達到了DA+IVTCG的4.3倍。由于此時光源深度較深,且處于高吸收低散射的肝臟內部,SP3+IVTCG更加適用于這種情況。

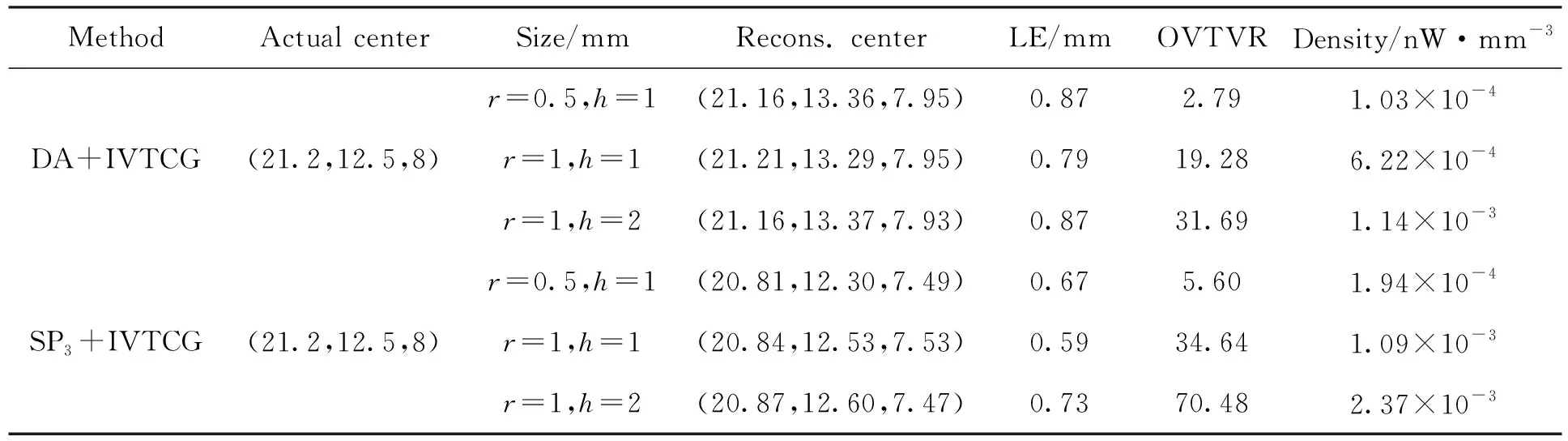
第二組實驗對比了兩種重建方法在高散射低吸收組織內的光源重建能力。將不同尺寸的單光源置于肺中,中心位置設定為(21.2,12.5,8)mm,相對于數字鼠背部表面深度為8.5mm,相對于數字鼠腹部表面深度為9.5mm,圖4展示了重建結果的截面視圖,表3對比了兩種方法得到的具體定量重建結果。盡管這組光源置于散射占主導地位的生物組織中,且距離外部邊界大于幾個平均自由程[11],屬于DA模型較為適用的情形,但從圖4以及表3的重建結果可以看出,SP3+IVTCG仍得到了優于DA+IVTCG的重建結果,只是優勢沒有在高吸收介質中那么明顯。

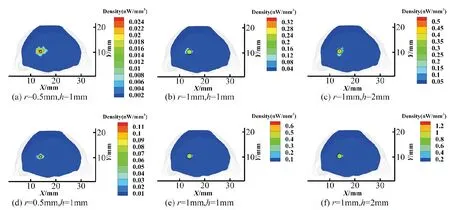
圖2 DA+IVTCG和SP3+IVTCG對中心在(14,10.5，16.6)mm處的不同尺寸單光源的重建結果。(a)～(c)是DA+IVTCG的重建結果在真實光源中心z=16.6mm處的截面視圖,其中黑色圓圈為真實光源位置。(d)～(f)是SP3+IVTCG對應的重建結果。Fig.2 The reconstruction results of different single sources centered at (14,10.5，16.6)mm by DA+IVTCG and SP3+IVTCG.(a)～(c) are the section views at z=16.6mm of the reconstruction results by DA+IVTCG, where the black circles denote the real light sources.(d)～(f) are the corresponding reconstruction results by SP3+IVTCG.

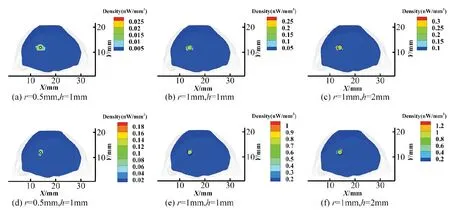
圖3 DA+IVTCG和SP3+IVTCG對中心位于(14,12，16.6)mm處的不同尺寸單光源的重建結果。(a)～(c)是DA+IVTCG的重建結果在真實光源中心z=16.6mm處的截面視圖,其中黑色圓圈為真實光源位置。(d)～(f)是SP3+IVTCG對應的重建結果。Fig.3 The reconstruction results of different single sources centered at (14,12，16.6)mm by DA+IVTCG and SP3+IVTCG.(a)～(c) are the section views at z=16.6mm of the reconstruction results by DA+IVTCG, where the black circles denote the real light sources.(d)～(f) are the corresponding reconstruction results by SP3+IVTCG.

MethodActual centerSize/mmRecons. centerLE/mmOVTVRDensity/nW·mm-3r=0.5,h=1(14.28,8.57,16.48)0.651.477.44×10-5(14,8,16.6)r=1,h=1(14.25,8.53,16.26)0.619.154.00×10-4r=1,h=2(14.50,8.22,16.37)0.6017.578.06×10-4r=0.5,h=1(13.22,10.79,16.46)0.851.056.49×10-5DA+IVTCG(14,10.5,16.6)r=1,h=1(13.33,10.73,16.50)0.7111.743.53×10-4r=1,h=2(13.76,10.73,16.19)0.5317.447.36×10-4r=0.5,h=1(13.69,11.72,17.21)0.741.106.20×10-5(14,12,16.6)r=1,h=1(13.65,11.68,17.08)0.678.703.48×10-4r=1,h=2(13.68,11.70,17.20)0.7413.407.34×10-4r=0.5,h=1(14.00,7.85,16.12)0.502.892.35×10-4(14,8,16.6)r=1,h=1(13.82,7.92,16.25)0.4028.601.35×10-3r=1,h=2(13.89,7.93,16.09)0.5238.492.39×10-3r=0.5,h=1(13.50,10.37,16.56)0.521.761.27×10-4SP3+IVTCG(14,10.5,16.6)r=1,h=1(13.89,10.38,16.67)0.1813.796.51×10-4r=1,h=2(13.79,10.45,16.76)0.2922.071.59×10-3r=0.5,h=1(13.87,11.71,16.60)0.324.741.47×10-4(14,12,16.6)r=1,h=1(13.78,11.72,16.52)0.3723.468.14×10-4r=1,h=2(13.61,11.78,16.24)0.5843.621.67×10-3

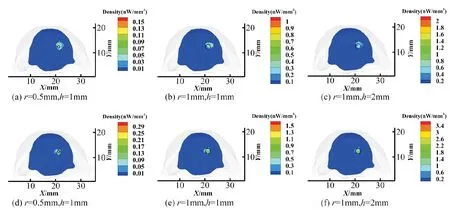
圖4 DA+IVTCG和SP3+IVTCG對中心在(21.2,12.5,8)mm處的不同尺寸單光源的重建結果。(a)～(c)是DA+IVTCG的重建結果在真實光源中心z=8mm處的截面視圖,其中黑色圓圈為真實光源位置。(d)～(f)是SP3+IVTCG對應的重建結果。Fig.4 The reconstruction results of different single sources centered at(21.2，12.5，8)mm by DA+IVTCG and SP3+IVTCG.(a)～(c) are the section views at z=8mm of the reconstruction results by DA+IVTCG, where the black circles denote the real light sources.(d)～(f) are the corresponding reconstruction results by SP3+IVTCG.

MethodActual centerSize/mmRecons. centerLE/mmOVTVRDensity/nW·mm-3r=0.5,h=1(21.16,13.36,7.95)0.872.791.03×10-4DA+IVTCG(21.2,12.5,8)r=1,h=1(21.21,13.29,7.95)0.7919.286.22×10-4r=1,h=2(21.16,13.37,7.93)0.8731.691.14×10-3r=0.5,h=1(20.81,12.30,7.49)0.675.601.94×10-4SP3+IVTCG (21.2,12.5,8)r=1,h=1(20.84,12.53,7.53)0.5934.641.09×10-3r=1,h=2(20.87,12.60,7.47)0.7370.482.37×10-3

2.2 雙光源仿真實驗

為了進一步測試兩種重建方法對多目標的分辨能力,本文設計了雙光源實驗,相同大小的雙光源被置于數字鼠的肝臟中,光源邊緣間的距離為3mm,光源大小與單光源仿真設置一致。本組實驗仍然測試了3種不同尺寸的光源,為了保持雙光源邊緣距離不變,不同大小光源的中心點位置不同,在光源為r=0.5mm,h=1mm時,雙光源的中心點為(14,8,17)mm和(14,12,17)mm,在光源大小為r=1mm,h=1mm以及r=1mm,h=2mm時,雙光源的中心點設置為(14,7.5,17)mm和(14,12.5,17)mm。

圖5和圖6分別展示了3組不同尺寸的雙光源重建結果的截面圖和3D視圖。從圖5，圖6和表4的重建結果可以看出,SP3+IVTCG在所有的光源設置下,均能得到2個較為均勻的重建目標,中心定位和形狀擬合都明顯優于DA+IVTCG。尤其是對較大尺寸的光源,SP3+IVTCG比DA+IVTCG更能準確地反應光源的形狀。在雙大光源時,SP3+IVTCG重建的兩個光源的OVTVR分別是DA+IVTCG的1.22和2.46倍。

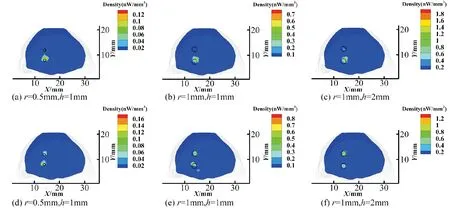
圖5 DA+IVTCG和SP3+IVTCG雙光源重建結果在光源中心所在位置的截面視圖(z=17mm),其中黑色圓圈為真實光源位置。(a)～(c)是DA+IVTCG的重建結果,(d)～(f)是SP3+IVTCG的重建結果Fig.5 Section views (z=17mm) of the reconstruction results by DA+IVTCG和SP3+IVTCG, where the black circles denote the real light sources.(a)～(c) are the reconstruction results of DA+IVTCG,(d)～(f) are the reconstruction results of SP3+IVTCG.

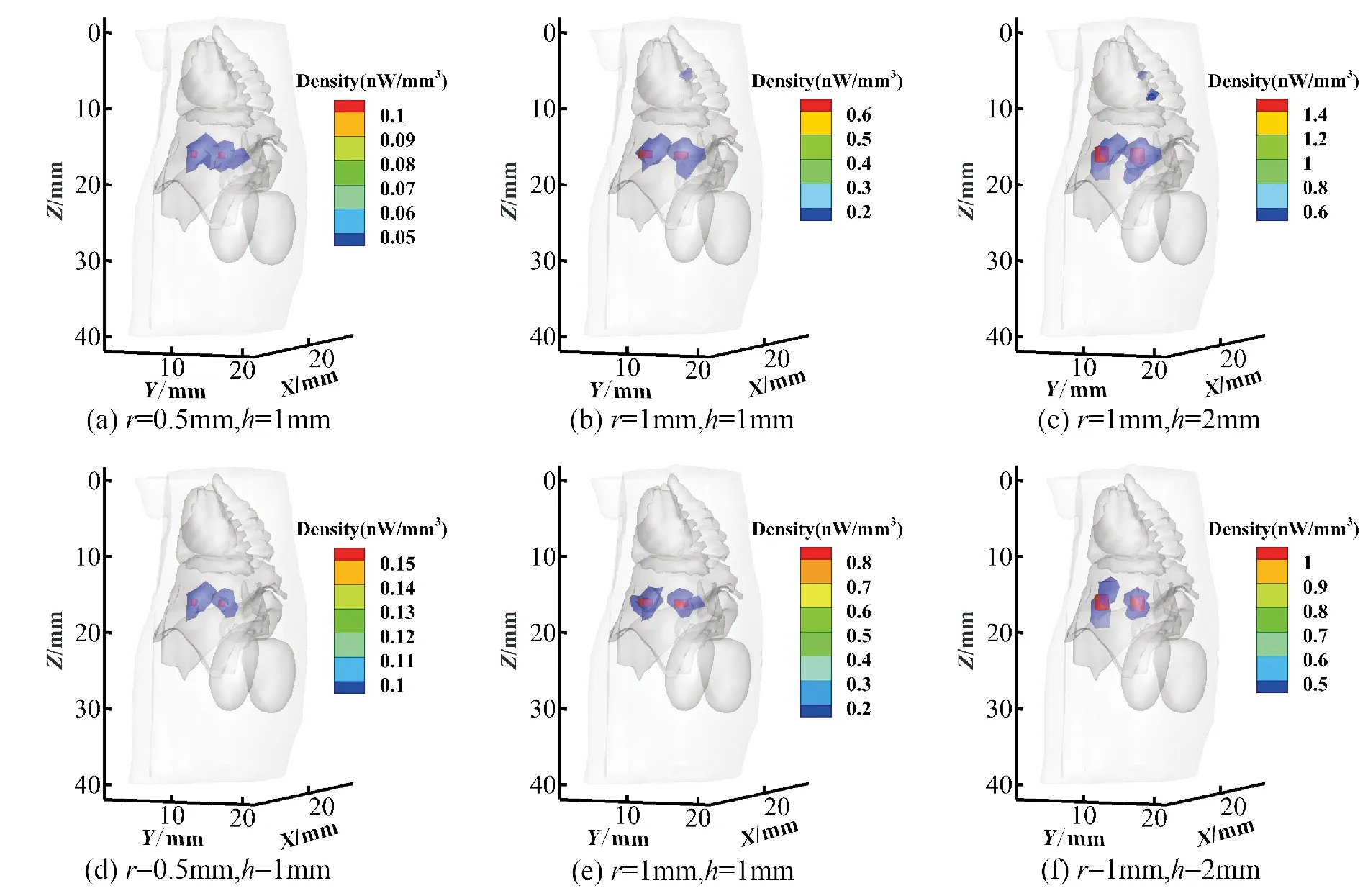
圖6 DA+IVTCG和SP3+IVTCG雙光源重建結果的3D視圖,其中紅色圓柱體為真實光源。(a)～(c)是DA+IVTCG的重建結果,(d)～(f)是SP3+IVTCG的重建結果Fig.6 3D views of the reconstruction result of DA+IVTCG and SP3+IVTCG, where the red cylinder are the real light sources.(a)～(c) are the reconstruction results of DA+IVTCG,(d)～(f) are the corresponding results of SP3+IVTCG

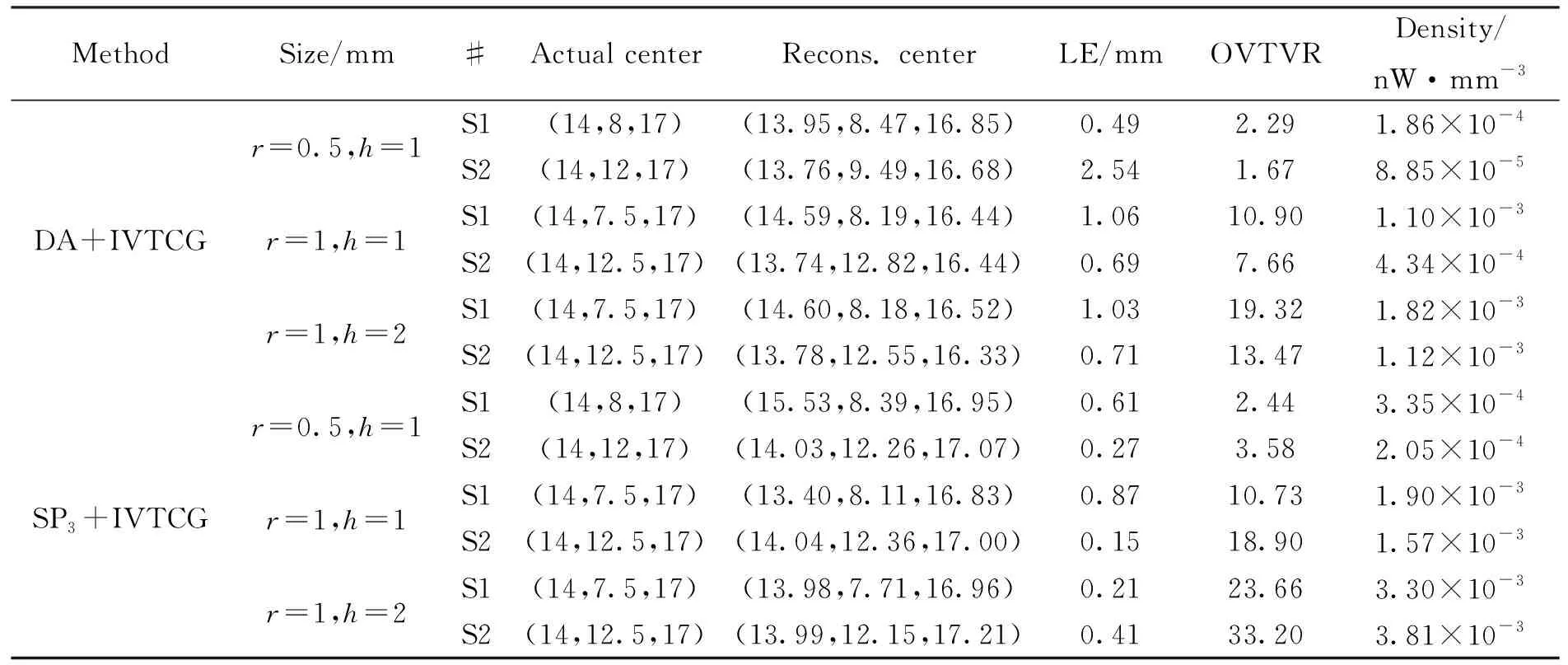
MethodSize/mm#Actual centerRecons. centerLE/mmOVTVR Density/nW·mm-3r=0.5,h=1 S1(14,8,17)(13.95,8.47,16.85)0.492.291.86×10-4S2(14,12,17)(13.76,9.49,16.68)2.541.678.85×10-5DA+IVTCGr=1,h=1 S1(14,7.5,17)(14.59,8.19,16.44)1.0610.901.10×10-3S2(14,12.5,17)(13.74,12.82,16.44)0.697.664.34×10-4r=1,h=2 S1(14,7.5,17)(14.60,8.18,16.52)1.0319.321.82×10-3S2(14,12.5,17)(13.78,12.55,16.33)0.7113.471.12×10-3r=0.5,h=1 S1(14,8,17)(15.53,8.39,16.95)0.612.443.35×10-4S2(14,12,17)(14.03,12.26,17.07)0.273.582.05×10-4SP3+IVTCGr=1,h=1 S1(14,7.5,17)(13.40,8.11,16.83)0.8710.731.90×10-3S2(14,12.5,17)(14.04,12.36,17.00)0.1518.901.57×10-3r=1,h=2 S1(14,7.5,17)(13.98,7.71,16.96)0.2123.663.30×10-3S2(14,12.5,17)(13.99,12.15,17.21)0.4133.203.81×10-3

3 結論

本文利用多光譜測量數據,結合L1范數正則化IVTCG算法,比較了基于SP3和基于DA的光源重建方法對重建光源形狀擬合程度的影響。單光源的仿真實驗結果表明,在高散射低吸收的區域,SP3+IVTCG在形狀以及重建光源的能量密度上優于DA+IVTCG,在非散射主導的區域內,SP3+IVTCG的優勢更加明顯,這是由于SP3更加適用于非散射主導的區域,光源深度越深,重建對于光傳輸模型的準確性的依賴越強,這種優勢越明顯。雙光源實驗對比了兩種方法的光源分辨能力,SP3+IVTCG重建的兩個光源比DA+IVTCG重建的兩個光源形狀更加近似,平均能量密度更加相當,定位也更加準確。