拓撲絕緣體中的拓撲不變量及其數(shù)值計算

孫 倩, 何院耀

(1.西北大學 物理學院,陜西 西安 710127；2.中國人民大學 物理學系,北京 100872)

拓撲量子態(tài)中沒有自發(fā)對稱性破缺,也沒有局域序參量,因而不能用Landau-Ginzburg理論來描述[1-6]。因此,我們需要用某種“全局序參量”來描述拓撲相的物理性質,就是整數(shù)化的拓撲不變量。物理上,拓撲不變量與拓撲相中量子化的霍爾電導率直接相關,比如量子霍爾效應中的霍爾電導率和拓撲絕緣體(量子自旋霍爾效應)中的自旋霍爾電導率。

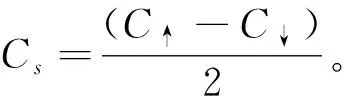
(1)

在下文中,用C表示系統(tǒng)自旋向上或自旋向下部分的陳數(shù)，而在具體數(shù)值計算中分別計算C↑和C↓，并得到拓撲不變量自旋陳數(shù)Cs。由于拓撲不變量只在零溫有良好定義,因此，本文的計算都是在零溫,對于系統(tǒng)基態(tài)的計算。

1 拓撲不變量計算公式

1.1 3種常用公式及其適用條件

針對不同的系統(tǒng),二維系統(tǒng)中陳數(shù)C有多種不同的計算公式,最常見的有以下3種。

第1種計算公式是非常著名的TKNN不變量,在文獻[4]中首次從能帶理論出發(fā)被推導出來。TKNN不變量的原始表達式為

Pst=

(2)

其中,波矢k=(kx,ky),BZ表示倒空間布里淵區(qū)，H=H(k)為系統(tǒng)倒空間哈密頓量(矩陣),|t〉，|s〉和Et(k),Es(k)分別為布洛赫本征態(tài)和相應的本征能量，即有

H(k)|s〉=Es(k)|s〉H(k)|t〉=Et(k)|t〉。

(3)

TKNN不變量可以進一步寫成Berry曲率在系統(tǒng)布里淵區(qū)上的積分,如下

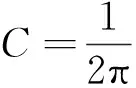
(4)

其中，Ωxy(k)為Berry曲率,a∈Occ表示被占據(jù)的能帶。

第2種是專門針對兩能帶系統(tǒng)的計算公式。兩能帶系統(tǒng)哈密頓量可以簡化為H(k)=d(k)·σ+d0(k),其中矢量d(k)=[dx(k),dy(k),dz(k)],σ=(σx,σy,σz)為泡利矩陣組成的矢量,d0(k)為與kx,ky相關的能量常數(shù)項(費米能級EF=d0(k))。則該兩能帶系統(tǒng)的陳數(shù)[5]可以表示為

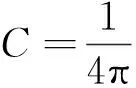
(5)

其中，

d=|d(k)| =

第3種是從零頻率單粒子格林函數(shù)G(ω=0,k)矩陣出發(fā)構造的陳數(shù)計算公式[10-18],其表達式為

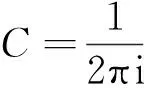
Tr{P(k)[?kxP(k)·?kyP(k)-

?kyP(k)·?kxP(k)]}。

(6)

其中，P(k)是由G(ω=0,k)矩陣本征值大于0的本征態(tài)構造的投影矩陣

G(0,k)|μi(k)〉=μi|μi(k)〉，

(7)

式(6)中Tr表示對矩陣求跡。

由上面3種不同的拓撲不變量的表達式可以看出,拓撲不變量是對布里淵區(qū)的積分,體現(xiàn)出其非局域性。式(4)中的TKNN不變量公式表明,只有費米能級處于系統(tǒng)的能隙中才能得到整數(shù)化的陳數(shù),即整數(shù)化的拓撲不變量只對于絕緣體才有意義。從計算角度看,第1種計算式(2)需要得到系統(tǒng)的倒空間哈密頓量矩陣,并對角化得到本征值和本征態(tài);第2種計算式(5)需要將倒空間2×2哈密頓量矩陣寫成d矢量的形式;第3種計算式(6)需要先計算零頻率的單粒子格林函數(shù)矩陣,然后構造P(k)投影矩陣;之后的積分計算對于3種公式是相似的。從物理角度看,雖然式(5)只能用于計算兩能帶系統(tǒng)的拓撲不變量,但是計算相對更簡單;式(2)和式(6)均可用于一般的多能帶系統(tǒng)。從公式的可擴展性看,式(2)和式(5)均是直接從無相互作用推導而來,只能用于計算無相互作用系統(tǒng)陳數(shù);式(6)從單粒子格林函數(shù)出發(fā),可以自然地用于有電子相互作用的系統(tǒng)中。

1.2 3種計算公式等價性的證明

根據(jù)上面3種不同的陳數(shù)計算公式，接下來證明在無相互作用系統(tǒng)中，式(2)、式(4)和式(5)、式(6)是等價的。

首先，證明在無相互作用兩能帶系統(tǒng)中，式(2)和式(5)的等價性。兩能帶系統(tǒng)的倒空間哈密頓量可表示為H(k)=d(k)·σ+d0(k),可得到其兩個本征能級和本征態(tài),分別為

E±(k)=d0(k)±d(k)，

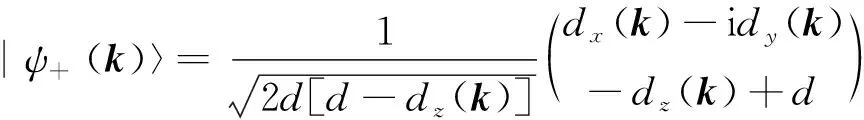
(8)

系統(tǒng)的費米能級EF=d0(k)。式(2)中求和要求EsEF,則有Es=E-(k),Et=E+(k),帶入式(2)可得

(9)

計算倒空間哈密頓量矩陣的一階導數(shù)?kxH(k)和?kyH(k)得到

〈ψ-|?kiH(k)|ψ+〉=

〈ψ+|?kiH(k)|ψ-〉=

(10)

其中，ki=kx,ky。根據(jù)式(10),可以得到

〈ψ-|?kxH(k)|ψ+〉〈ψ+|?kyH(k)|ψ-〉-

〈ψ+|?kxH(k)|ψ-〉〈ψ-|?kyH(k)|ψ+〉=

[〈ψ-|σα|ψ+〉〈ψ+|σβ|ψ-〉-

〈ψ-|σβ|ψ+〉〈ψ+|σα|ψ-〉]=

〈ψ-|[σα,σβ]|ψ-〉。

(11)

式(11)中的求和共有9項,但是，由于[σγ,σγ]=0,γ=x,y,z,其中只有6項不為零。將式(8)中的兩個本征態(tài)波函數(shù)代入式(11),可得

〈ψ-|?kxH(k)|ψ+〉〈ψ+|?kyH(k)|ψ-〉-

〈ψ+|?kxH(k)|ψ-〉〈ψ-|?kyH(k)|ψ+〉=

2i{(?kxdx?kydy-?kxdy?kydx)·〈ψ-|σz|ψ-〉+

(?kxdz?kydx-?kxdx?kydz)·〈ψ-|σy|ψ-〉+

(?kxdy?kydz-?kxdz?kydy)·〈ψ-|σx|ψ-〉}=

(?kxdz?kydx-?kxdx?kydz)·dy+

(?kxdy?kydz-?kxdz?kydy)·dx}。

(12)

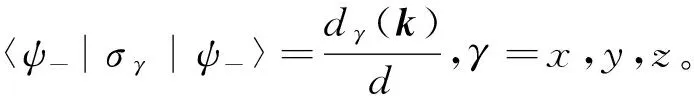
d·[(?kxd)×(?kyd)]=

dz(?kxdx?kydy-?kxdy?kydx)+

dy(?kxdz?kydx-?kxdx?kydz)+

dx(?kxdy?kydz-?kxdz?kydy)。

(13)

將式(12)和式(13)代入式(9)得到

(14)

最后，將式(14)的結果代入到式(2)即得到

(15)

式(15)即為第2種陳數(shù)計算式(5),由此即證明了式(2)和式(5)在兩能帶系統(tǒng)中的等價性。

其次，證明在無相互作用系統(tǒng)中公式(4)和公式(6)的等價性。首先，需要計算動量空間單粒子格林函數(shù)矩陣G(ω,k),其中ω為一般的復頻率。利用格林函數(shù)運動方程方法可以得到無相互作用系統(tǒng)G(ω,k)表達式

G(ω,k)=[ω-H(k)]-1。

(16)

其中，H(k)同上為倒空間哈密頓量矩陣。則有零頻率單粒子格林函數(shù)G(ω=0,k)表達式為

G(ω=0,k)=-[H(k)]-1。

(17)

可見G(ω=0,k)和H(k)矩陣有相同的本征態(tài),且本征值有相應變換關系

H(k)|a(k)〉=Ea(k)|a(k)〉，

G(0,k)|a(k)〉=-[H(k)]-1|a(k)〉=

-[Ea(k)]-1|a(k)〉。

(18)

將式(18)代入式(7)可得

(19)

根據(jù)式(19)可以計算P(k)的一階導數(shù)如下

|b(k)〉〈?kxb(k)|)，

|c(k)〉〈?kyc(k)|)。

(20)

進一步公式(6)中的Trace可以用完備的本征波函數(shù)展開來計算,如

Tr[P(k)TxTy]=

Tr[P(k)TyTy]=

(21)

其中，∑k|e(k)〉〈e(k)|=1。在式(21)中,將式(19)結果代入可得

〈e(k)|P(k)=

(22)

將式(22)代入式(21)可得

(23)

式(6)中Trace部分可簡化為

Tr{P(k)[?kxP(k)?kyP(k)-

?kyP(k)?kxP(k)]}=

(24)

根據(jù)式(24)結果，需要計算TxTy和TyTx。利用式(20)得到TxTy表達式

TxTy=

|b(k)〉〈?kxb(k)||?kyc(k)〉〈c(k)|+

|b(k)〉〈?kxb(k)||c(k)〉〈?kyc(k)|}+

(25)

以及TyTx表達式

TyTx=

|c(k)〉〈?kyc(k)||?kxb(k)〉〈b(k)|+

|c(k)〉〈?kyc(k)||b(k)〉〈?kxb(k)|}+

(26)

可見TxTy和TyTx表達式的求和中均有4項,其中三項是二重求和,一項是一重求和。將式(25)和式(26)結果代入式(24)可得

〈?kye(k)||?kxe(k)〉]+

〈e(k)||?kyb(k)〉〈?kxb(k)||e(k)〉}。

(27)

式(27)兩項相減后,原TxTy和TyTx表達式求和中有兩項分別抵消,剩余兩項,即為式(27)結果。注意到式(27)結果第二項(即二重求和項)等于0,原因為

〈e(k)||?kxb(k)〉+〈?kxe(k)||b(k)〉=

?kx[〈e(k)||b(k)〉]=0，

〈?kyb(k)||e(k)〉+〈b(k)||?kye(k)〉=

?ky[〈b(k)||e(k)〉]=0。

(28)

由式(28)可得

〈e(k)||?kxb(k)〉=-〈?kxe(k)||b(k)〉，〈?kyb(k)||e(k)〉=-〈b(k)||?kye(k)〉。

(29)

結合式(29)可以得到

(30)

其中，最后一步相等可理解為將第二步第一項求和中b和d互換,即與第二項求和完全相同,所以結果為0。結合式(24)、式(27)和式(30),可得

Tr{P(k)[?kxP(k)?kyP(k)-

?kyP(k)?kxP(k)]}=

〈?kye(k)||?kxe(k)〉]。

(31)

根據(jù)式(4)可計算Berry曲率

〈?kya(k)||?kxa(k)〉]。

(32)

結合式(31)和式(32)得到

Tr{P(k)[?kxP(k)?kyP(k)-

?kyP(k)?kxP(k)]}=iΩxy(k)。

(33)

最后將式(33)結果代入式(6),即得到

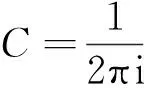
Tr{P(k)[?kxP(k)·?kyP(k)-?kyP(k)·?kxP(k)]}=

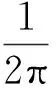
(34)

式(34)結果即為式(4),亦即式(2),由此證明了式(34)與式(2)和式(4)的等價性。

通過以上解析計算,可以發(fā)現(xiàn)上述3種不同的計算陳數(shù)的公式在無相互作用系統(tǒng)中是完全等價的。其中,式(2)和式(6)也可用于計算多能帶系統(tǒng)拓撲不變量;式(6)還可以拓展應用于有相互作用系統(tǒng)中拓撲不變量的計算。

2 應用實例:Kane-Mele模型

2.1 數(shù)值計算細節(jié)

下面以具體模型為例討論上述拓撲不變量的數(shù)值計算。由于第3種計算式(6)的廣泛適用性,在以下的計算中均選用式(6)做數(shù)值計算。式(2)、式(4)和式(5)的數(shù)值計算與式(6)很相似,這里不做討論。為不失普遍性,我們選取一般化的Kane-Mele模型(honeycomb晶格)作計算,模型哈密頓量如下

(35)

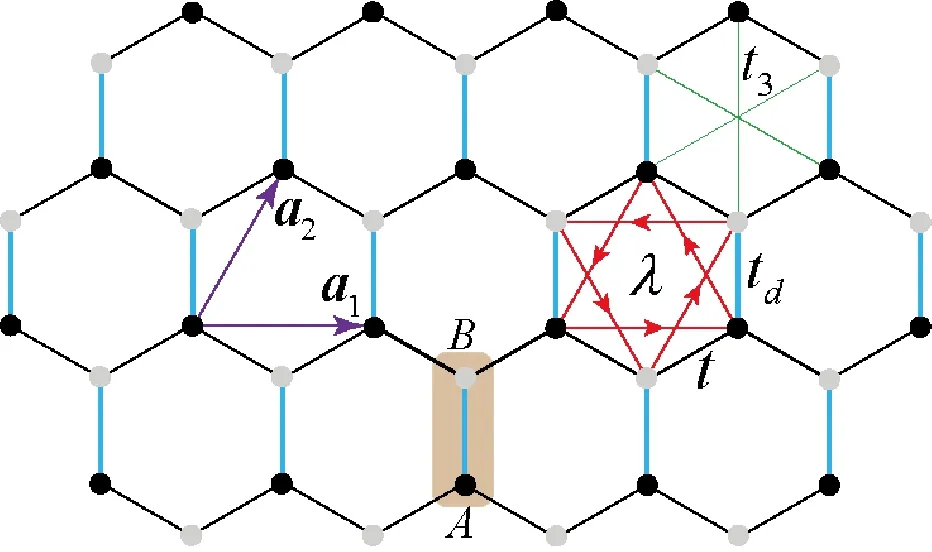
圖1 二維honeycomb晶格以及Kane-Mele模型中各項電子躍遷示意圖Fig.1 Lattice geometry of 2D honeycomb lattice with hopping parameters in Kane-Mele model

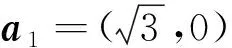
[H(k)]σ=

g(k)=

(36)

其中,自旋向上ξ↑=+1和自旋向下ξ↓=-1。式(6)的數(shù)值計算中需要計算布里淵區(qū)上的積分,我們用最簡單的梯形法作積分,但是，由于honeycomb晶格的布里淵區(qū)是平行四邊形,而不是矩形,首先，需要做一個Jacobi變換,將系統(tǒng)的布里淵區(qū)變成一個矩形,再用梯形法作數(shù)值積分。一般地,任何非正方晶格的布里淵區(qū)均可由Jacobi變換變成矩形,所以下面的計算可以推廣到所有晶格的情形。honeycomb晶格的布里淵區(qū)邊界為

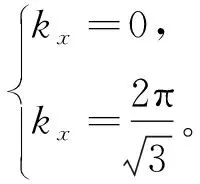
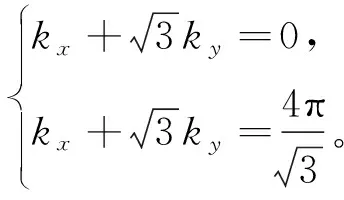
(37)

引入如下的Jacobi變換以及逆變換

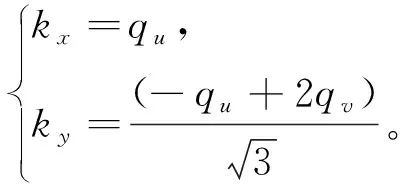
(38)

可得新變量qu,qv取值范圍為矩形,即

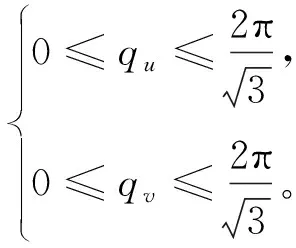
(39)

這個Jacobi變換相應的Jacobi行列式為

(40)

綜合式(37)～(40),在honeycomb晶格的布里淵區(qū)上的積分可以轉化為矩形區(qū)域的積分

I=?k∈BZf(kx,ky)dkxdky=

(41)

其中，有

(42)

將式(41)和式(42)代入式(6)可得

C=?k∈BZf(kx,ky)dkxdky=

(43)

其中，

Tr{P(k)[?kxP(k)·?kyP(k)-?kyP(k)·?kxP(k)]}。

(44)

為方便數(shù)值計算，需要將P(k)對kx和ky的一階導數(shù)轉化為對qu和qv的一階導數(shù)。引入Q(qu,qv)函數(shù)矩陣，

Q(qu,qv)。

(45)

計算P(k)對kx和ky的一階導數(shù)為

(46)

將式(46)代入式(44),得到

Tr{P(k)[?kxP(k)·

?kyP(k)-?kyP(k)·?kxP(k)]}=

(47)

將式(47)代入式(43)，即可得到陳數(shù)表達式為

?quQ]}。

(48)

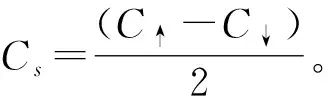
2.2 計算結果

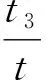
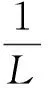
2)在每個對應的絕緣體相中,自旋陳數(shù)在熱力學極限下都是整數(shù)化(量子化)的;

3)在不同絕緣體之間的拓撲相變處,自旋陳數(shù)具有跳變,這個跳變是拓撲相變基本的特點之一。

由此可見,上述自旋陳數(shù)Cs有效和正確地描述了Kane-Mele模型的完整相圖。

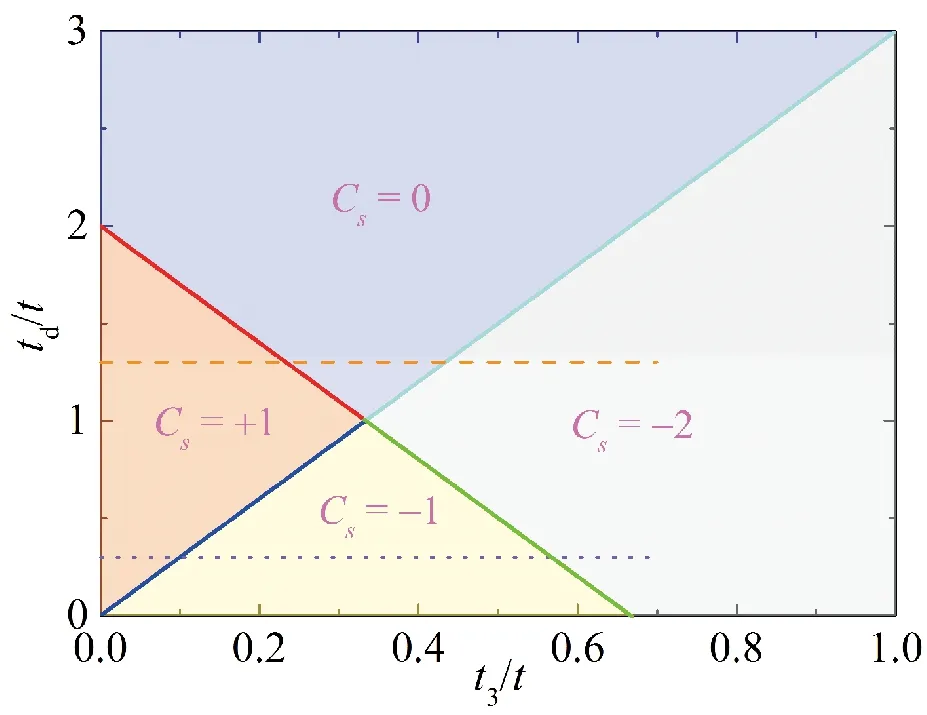
圖2 Kane-Mele模型t3-td相圖(λ=0.2t)Fig.2 The t3-td phase-diagram of Kane-Mele model with λ=0.2t

通過以上Kane-Mele模型中拓撲不變量的計算,檢驗了上述拓撲不變量的計算范式,展示了計算方法的正確性。

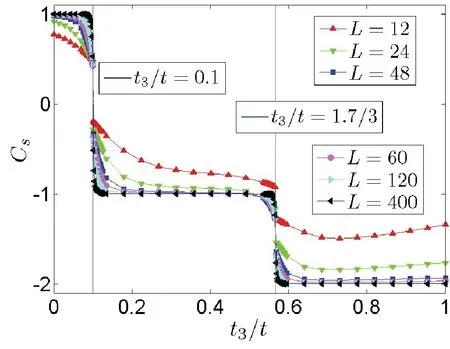
圖自旋陳數(shù)Cs的計算結果Fig.3 Results of calculated spin Chern number Cs for with λ=0.2t

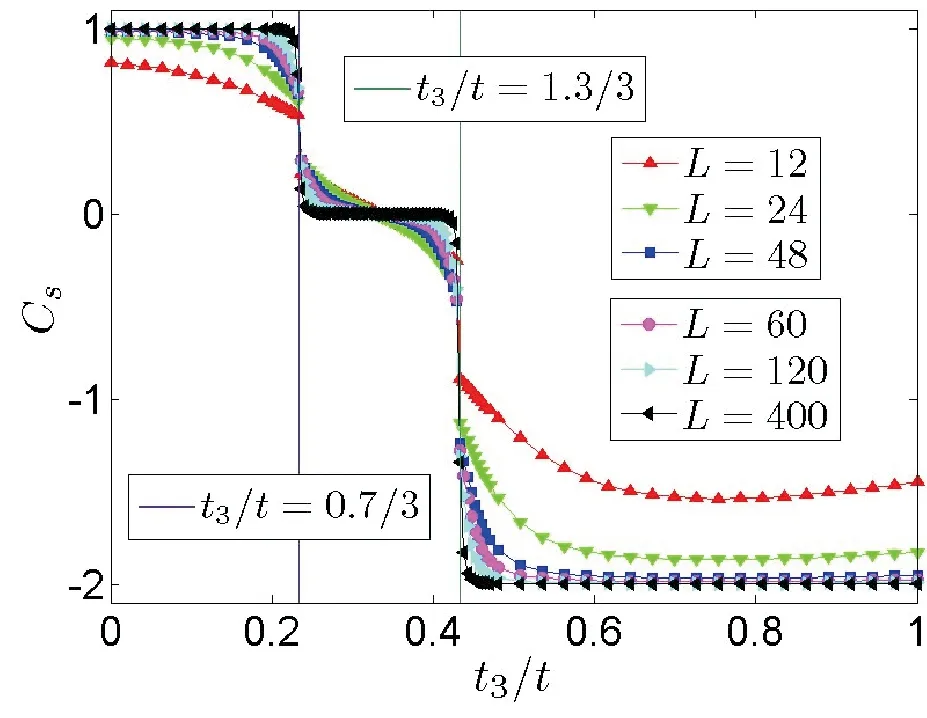
圖自旋陳數(shù)Cs的計算結果Fig.4 Results of calculated spin Chern number Cs for with λ=0.2t

3 結 語

首先，證明了在無相互作用系統(tǒng)中,常用到的3種拓撲不變量計算公式的等價性,并給出了詳細的證明推導過程;其次,我們給出了從零頻率單粒子格林函數(shù)出發(fā)推導的拓撲不變量公式的完整數(shù)值計算過程;最后，用拓撲不變量公式做了Kane-Mele模型中拓撲不變量的數(shù)值計算,根據(jù)拓撲不變量的值計算出了Kane-Mele模型的完整相圖,展示了本文中闡述的計算拓撲不變量方法的有效性和正確性。本文的工作對于無相互作用拓撲絕緣體系統(tǒng)的研究,特別是分類有比較重要的意義。此外,何院耀在文獻[19-20]中詳細研究了利用式(6)結合量子多體數(shù)值計算方法(如量子蒙特卡洛算法)計算有相互作用拓撲絕緣體系統(tǒng)的拓撲不變量，與本文的工作形成互補。這些工作連同本文工作一起,共同構成了計算拓撲絕緣體(無相互作用和有相互作用)系統(tǒng)中拓撲不變量的一套完整的方法,對于拓撲絕緣體的研究具有重要意義。