大型民用飛機氣動外形典型綜合設計方法

黃江濤，高正紅，余婧，鄭傳宇,*，周鑄

1.中國空氣動力研究與發展中心 計算空氣動力研究所，綿陽 621000 2.西北工業大學 航空學院，西安 710072

隨著高性能計算機與數值模擬技術的飛速發展，數值優化手段開始在飛行器氣動外形綜合設計中發揮重要作用。與傳統“Cut and Try”試湊不同，數值優化設計避免了數字化模型修型、網格劃分以及指標轉換迭代等繁瑣的重復性人工操作，極大程度上減少了設計結果驗證需要開展的風洞試驗次數，取而代之的是高效率的搜索算法、全自動化的網格重構以及智能決策體系等高效率模塊，很大程度上對氣動外形設計手段起到變革作用，促進了設計空氣動力學的發展，更進一步豐富了氣動優化設計的研究內容。

對于客機、運輸機、長航時無人機等大型飛機而言，先進的數值優化技術顯得尤為重要，尤其是大型民用飛機，氣動設計直接關系到飛機的巡航經濟性能，對民用飛機市場競爭力產生重要影響。與中小型飛機不同，大型飛機由于機體本身較大的參考面積，一個阻力單位(1 count=1.0×10-4)的減阻效果將帶來較為明顯的經濟效益，因此，大型民用飛機氣動設計更趨向于精細化，同時由于安全性等方面的要求，也更加注重于綜合性能設計。

精細化、多目標綜合設計是大型民用飛機設計的最明顯特征，這對傳統設計手段提出了挑戰，對于新一代遠程寬體飛機設計而言，巡航速度更高，在苛刻的設計要求條件下，由此帶來的設計難度更大。目前，應用于氣動外形綜合設計的優化手段主要包含兩類：基于非梯度信息類的氣動優化(如進化類算法、模式搜索算法等)[1-7]，以及基于梯度信息類的氣動優化[8-13]，每種方法均有各自的優缺點，在氣動設計領域均得到了一定程度的應用。尤其是基于伴隨方程的梯度類優化方法由于其極高的計算效率，倍受CFD工程師、氣動設計工程師以及氣動優化技術研發人員的關注，也是國內外空氣動力學研究機構一個重要的研究方向，且開展了基于伴隨方法的綜合優化設計，典型有代表性的研究工作有，密歇根大學Lyu等基于離散伴隨方法開展了CRM(Common Research Model)外形多點設計[14]，Kenway和Martins基于離散伴隨開展了包含抖振特性的多點設計研究[15]。如何有效利用各種方法的優點，實現飛行器氣動外形高效率綜合優化，對于工程應用來講，是一個值得探討的研究方向。

面向氣動外形多點綜合優化設計問題，本文基于課題組自主研發的飛行器氣動外形大規模并行化、分布式綜合設計軟件AMDEsign(Aircraft Multi-disciplinary DEsign)，結合主分量分析方法，研究了離散伴隨方法在典型寬體飛機模型氣動設計中應用研究，同時提出了基于“虛擬可行解”的權系數導向選擇方式，及其在離散伴隨多目標優化設計中應用的可行性，為氣動設計人員在優化策略選擇上提供一些有價值的參考。

1 AMDEsign飛行器多學科優化設計平臺簡介

本文的研究基于課題組面向航空航天飛行器自主研發的AMDEsign軟件平臺進行，該平臺是基于并行環境下研發的分布式大型優化設計代碼，可以應用于民用飛機、作戰飛機、進氣道、超聲速飛機聲爆抑制、旋翼/螺旋槳、高鐵減阻設計等航空航天、工業空氣動力設計工程領域。主要包含了基本功能、學科分析、伴隨體系、傳統體系等框架。幾個框架由優化決策模塊統一管理，其中：

1) 基本功能框架包含了網格重構、參數化建模等共用功能性模塊。

2) 學科分析框架主要包含了流場分析、氣動彈性、聲爆計算、結構分析等學科分析模塊。

3) 伴隨框架包含了流場伴隨、多學科耦合伴隨等模塊。

4) 傳統框架主要包含了試驗設計、代理模型等模塊。

本文基于平臺中的主分量分析、離散伴隨系統等模塊進行綜合設計方法研究。

2 高維目標空間優化問題

民用大飛機氣動設計需要綜合考慮巡航升阻比、阻力發散、力矩特性以及抖振邊界等問題，是典型的高維多目標優化問題。非支配解方法是處理多目標優化比較有效的手段。然而，在處理大于3個目標函數以上的優化問題時存在非支配解解集前沿推進速度慢、甚至不收斂，以及解集可視化水平不高等問題[16]。

針對該問題，課題組建立了基于主分量分析(Principal Component Analysis, PCA)的方法進行目標空間相關性分析、降維優化，在不失優化問題主特征的條件下，提取問題的主要特征，實現設計目標的有效降維，詳細計算原理，可參考文獻[16-17]，圖1給出了具體的分析流程，本文研究為提高優化設計效率，在大規模抽樣一次分析的基礎上，開展PCA相關性分析進行目標空間降維，進一步基于伴隨方法進行非冗余目標多目標優化分析。

3 基于“虛擬可行解”與伴隨方法的加權函數多目標優化設計

3.1 虛擬可行解方法

毫無疑問，基于離散伴隨方法的優化設計盡管在全局性優化問題上存在不足，但在高維設計變量精細化優化問題上具有傳統方法不具備的天然優勢，完全可以在飛行器氣動設計中扮演一種重要的角色。如何高效利用這種優勢開展多點優化是一個值得探討的研究方向。

對于基于梯度信息的多點數值優化設計來說，通常采用的是加權函數處理方式進行高效優化，構造空間目標函數：

F=ω1f1+ω2f2+ω3f3+……

(1)

式中：F為加權目標函數；ωi為各個目標函數的權重；fi為各個目標函數。容易看出，基于這種形式的優化設計結果嚴重依賴于權函數的選取，在面向具體設計指標開展優化時，權函數的選擇存在較大的盲目性。如何合理地、高效地選擇權函數是減小設計計算量、提高設計效率、有效滿足指標的關鍵因素，也是設計人員、優化決策系統最為關心的問題，尤其是基于靈敏度的優化設計，該問題顯現的更加突出，該項技術是最大程度上挖掘伴隨方法優化設計潛力的關鍵。

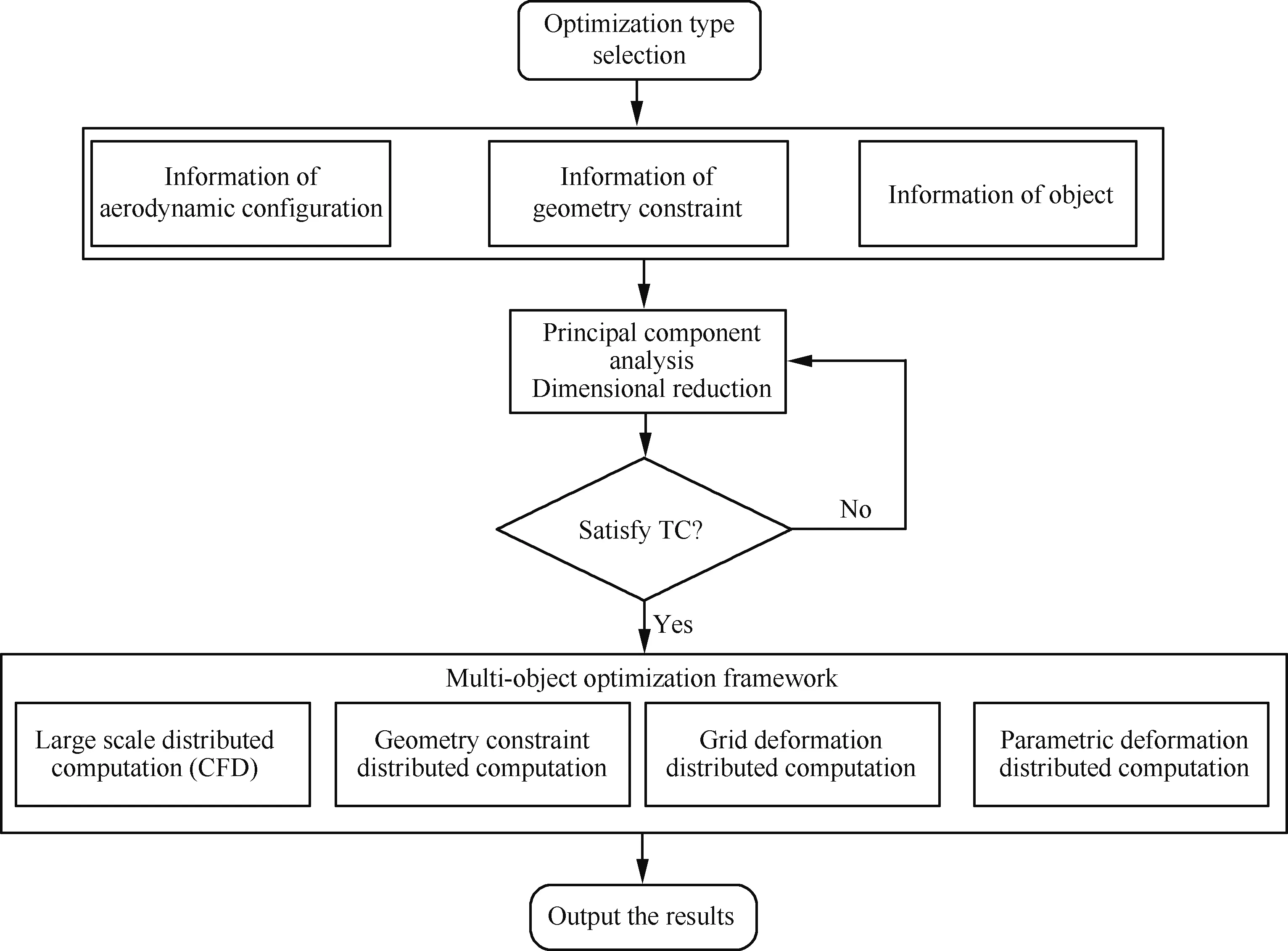
圖1 基于PCA方法的優化流程[17]Fig.1 Optimization process based on PCA method[17]

為此，本文提出了一種“虛擬可行解”導向性優化方法，其本質是對權函數進行抽樣，進行分布式加權優化設計，得到一組設計結果分布，利用神經網絡逼近構建虛擬的Pareto前沿，去尋找靠近設計指標要求的權函數組合。具體流程為

1) 對各個設計指標對應的權系數進行抽樣分析。與設計變量不同，由于目標函數個數遠小于設計變量，因此抽樣的個數并不需要太大。

2) 對不同權函數組合在并行環境下，進行獨立性優化，由于伴隨方法的高效性，此時的計算資源需求并不是很高。

3) 依據各個設計點的優化結果，利用合理數學模型逼近構造虛擬的可行解前沿。

4) 基于“虛擬可行解”前沿預測滿足設計指標的權重組合，開展多目標優化，并加入抽樣集合。

5) 根據優化結果，判斷是否滿足設計指標，如果滿足停止優化，否則，轉向步驟3)。

3.2 基于流場伴隨方程求解梯度

飛行器氣動優化設計中的最小化問題數學模型可以表達為

minI(W,X)

(2)

式中：目標函數I可以為升阻力、力矩、流量、壓比等參數；W、X分別為流場守恒變量、設計變量。顯然，在定常流場收斂解的條件下，殘差約束R(W,X)=0，進一步引入拉格朗日算子Λ重新構造目標函數：

L=I+ΛTR

(3)

利用鏈式求導對式(3)進行展開：

(4)

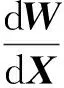
(5)

式(5)就是流場伴隨方程，通過隱式迭代方法求解拉格朗日算子Λ之后，可以通過式(6)進行目標函數梯度信息快速求解。

(6)

(7)

可以看出，伴隨方程求解完后，流場與伴隨變量均保持不變，基于有限差分的導數計算通過擾動設計變量實現，差分步長取1.0×10-4，流場不需要再迭代，此時計算量取決于變形網格計算效率與設計變量個數，由于文中采用了效率極高的并行化RBF-TFI (Radial Basis Functions，TransFinite Interpolation)網格變形技術，64進程并行環境下，處理千萬量級網格的時間小于5 s， 因此，此時的計算量可以忽略不計。

本文離散伴隨方程的結構采用二階精度的中心格式，人工黏性以及剪切應力輸運(SST)兩方程湍流模型，采用手工推導方式進行Navier-Stokes方程離散伴隨方程構造，并進一步引入虛擬時間項。對式(5)的迭代求解，采用LU-SGS方法隱式時間推進，離散伴隨方程各項的物理邊界條件采用矩陣形式，凍結湍流黏性系數，由于文中開展全湍流條件下的計算與優化，因此，盡管凍結湍流黏性系數帶來一定的誤差，但對于優化設計來講仍然能夠較為準確地給出下降方向進行有效設計。黏性項采用薄層近似，離散伴隨方程求解時并行機制依然采用與流場并行計算一致的單元數衡量的負載平衡、對等式計算以及MPI消息傳遞模式。其中，通過MPI進行傳遞的信息是伴隨變量。各個進程中分割面上的兩層虛網格上的伴隨變量信息以及對接邊界條件處理方式，詳細處理可以參考文獻[18]。

4 寬體飛機標準模型多目標優化與分析

基于寬體飛機CRM標準模型[19]為優化研究算例，進行本文方法的有效性驗證。不同的是，為方便進一步開展其他方面的研究，在CRM基礎上加入了立尾，且參考點位置與文獻[19]不同，但這并不影響本文綜合設計方法的有效性驗證。優化過程中主要部件同時包含機翼、機身、平尾以及立尾。網格劃分為290塊，半模網格規模為1 200萬量級，如圖2所示。流場求解采用自主研發的大規模并行CFD軟件PMB3D[20]，伴隨變量求解采用自主研發的大規模并行PADJ3D軟件[18]，進一步采用并行化RBF-TFI網格變形技術[21]進行梯度信息求解。計算過程采用中心格式，SST湍流模型，LU-SGS時間推進以及多重網格加速收斂技術，64核進行并行計算。關于CFD數值模擬以及伴隨梯度數值求解精度校核的具體細節詳見文獻[16,18]。

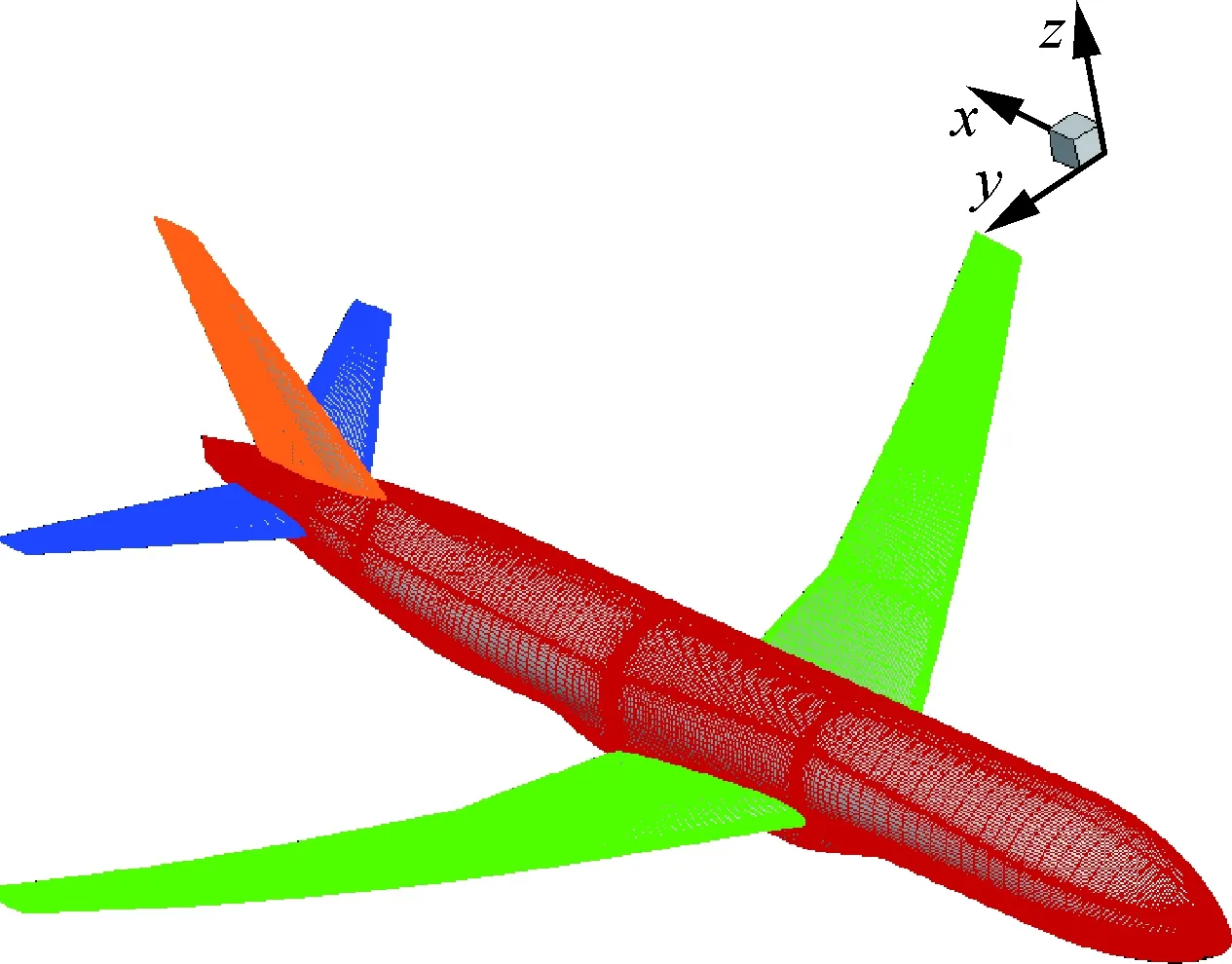
圖2 CFD表面網格分布Fig.2 CFD surface gird distribution

超臨界機翼采用了基于NURBS基函數的自由式變形(Free Form Deformation，FFD)進行參數化[21]，圖3給出了示意圖，共采用200個控制頂點實現機翼氣動外形參數化建模。該模型的設計要求是在滿足幾何約束的前提下，對巡航狀態升阻比、阻力發散特性、抖振邊界以及力矩特性進行綜合優化，設計狀態為Ma=0.85,Re=5.0×106，其初始優化數學模型為

CL,design=0.5

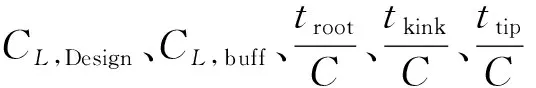
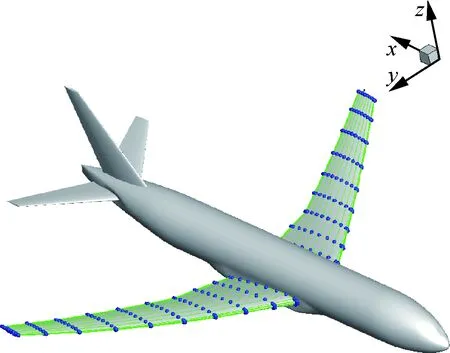
圖3 自由式變形參數化Fig.3 Parameterization of free form deformation

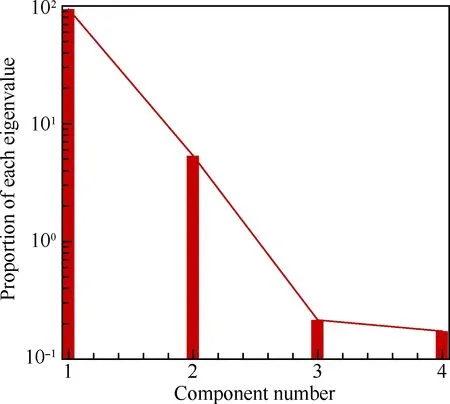
圖4 特征值分布Fig.4 Distribution of eigenvalue

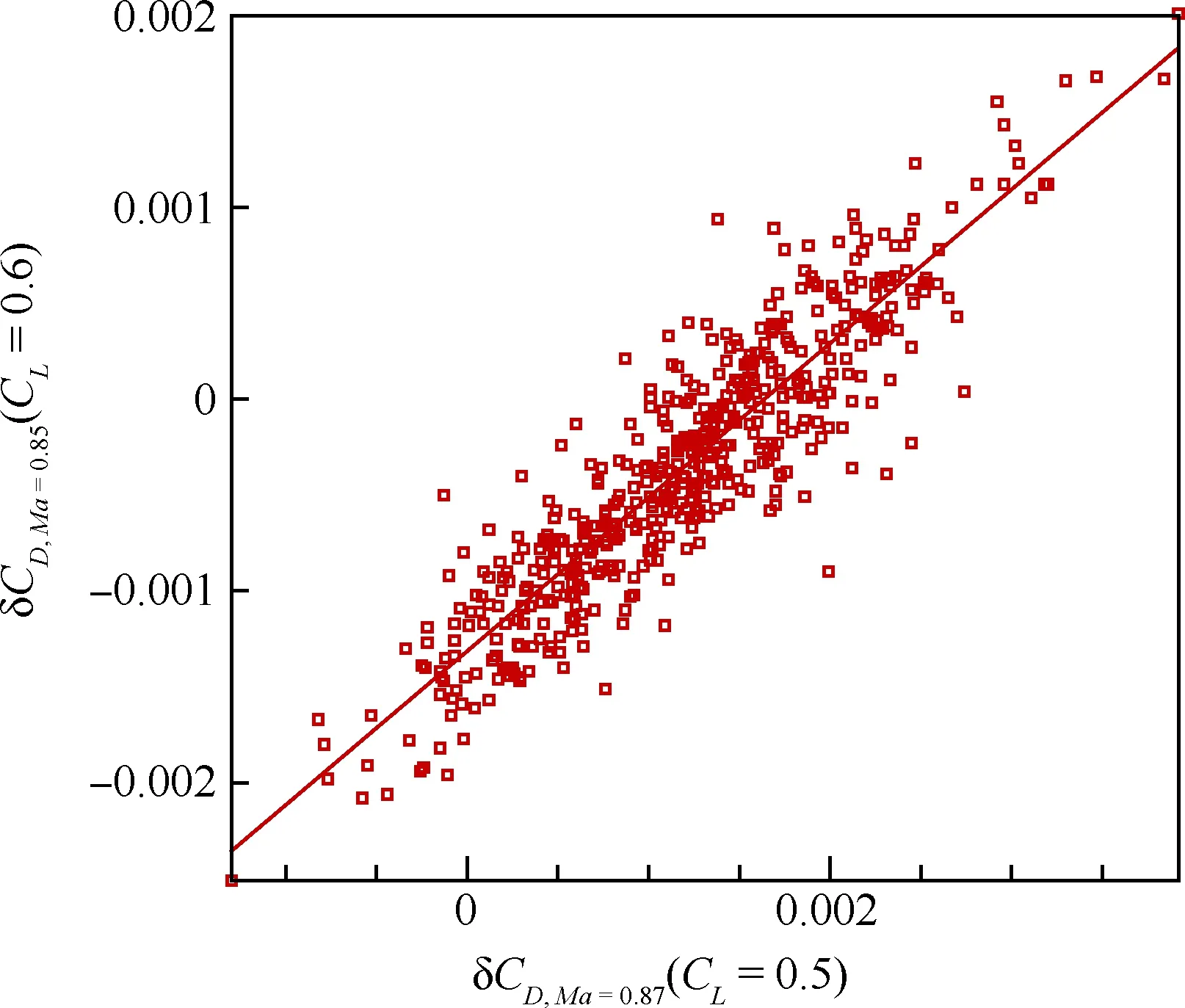
圖5 相關性分析Fig.5 Correlation analysis

0.87、CL=0.5狀態的阻力與Ma=0.85、CL=0.6狀態的阻力系數增量的相關性分析示意圖，這也是PCA的一個本質作用，即分析目標函數之間的相關性。

依據PCA相關性分析，最終選定f1、f2和f4兩個狀態為目標函數，其中力矩做約束處理，開展多點優化，并進一步對優化結果進行“冗余目標”驗證。

結合伴隨優化設計體系，建立加權形式的優化數學模型：

minF=ωf1+(1-ω)f2

式中：ω為權系數。

文中優化過程，為滿足升力系數的等式約束條件，采用了定升力系數計算，此時迎角隨設計變量變化而變化，是影響靈敏度計算的重要因素，且對靈敏度的計算具有變分貢獻，為避免對迎角求解靈敏度，需要消去該項的顯式表達[10]。對阻力系數變分：

(8)

進一步考慮升力約束δCL=0變分：

可以得到固定升力系數條件下，迎角變分表達式為

(9)

將式(9)代入式(8)可以得到定升力條件下的阻力系數靈敏度計算表達式：

(10)

基于序列二次規劃(SQP)算法，在中國空氣動力研究與發展中心1 590萬億次/秒的高性能集群上開展伴隨方法加權優化，不同權函數伴隨優化采用分布式計算，每個權函數的伴隨方法優化采用64核，共采用256核。在為虛擬Pareto 前沿構建提供不同權函數組合數據后，基于虛擬Pareto前沿選擇滿足0.85～0.87阻力增量不大于20 counts的權函數。

表1給出了設計前后不同外形在不同馬赫數的氣動特性對比，K表示升阻比，基于“虛擬前沿”導向性權重的多點優化設計在阻力發散特性方面有明顯改善，0.85～0.87阻力增量為19.1 counts，巡航升阻比也有明顯提高。圖6～圖7給出了單點優化以及多點優化與初始構型壓力系數云圖的對比。可以看出，單點優化完全消除表面激波，多點優化呈現弱激波形態。圖8給出了不同設計方法的優化歷程，紅線、綠線分別代表多點設計中Ma=0.85、Ma=0.87狀態阻力優化歷程曲線，藍線代表Ma=0.85單點優化歷程，各個方法均進行了20代 優化。圖9給出了展向絕對坐標Y=5、10、15、20 m站位壓力分布優化前后對比，相對于初始外形激波強度均大幅減弱，單點設計與多點設計壓力分布形態區別主要在kink外翼段。以Y=15 m站位壓力分布來分析，單點設計壓力分布呈無激波形態，阻力發散、抖振特性較好的多點設計氣動外形典型壓力分布形態壓力恢復位置較初始外形靠前，壓力恢復段呈現弱激波形態，緊跟一段較短的加速區(“鼓包狀壓力分布”)，如圖9(c)所示，該加速區再次恢復過程沒有出現第2道激波，實際上，該處加速區可以一定程度減緩馬赫數增大時激波強度的增加，對阻力發散較為有利。圖10給出了不同優化方法設計結果的阻力發散特性對比，圖11～圖13給出了不同外形的在CL=0.62下的表面極限流線，可以看出，初始外形已經大面積分離，單點優化與多點優化的流動均為小分離泡形式，一定程度上反映了抖振特性的改善，也驗證了文中綜合分析方法的可行性。

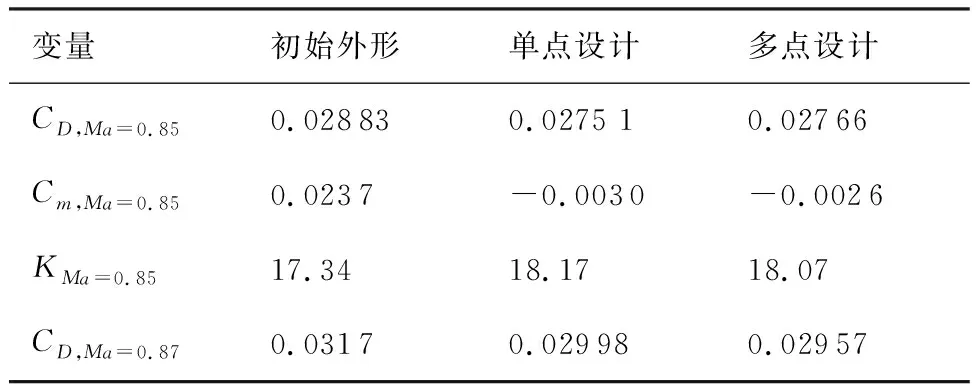
表1 不同設計結果氣動特性對比Table 1 Comparison of aerodynamic characteristics between different design results

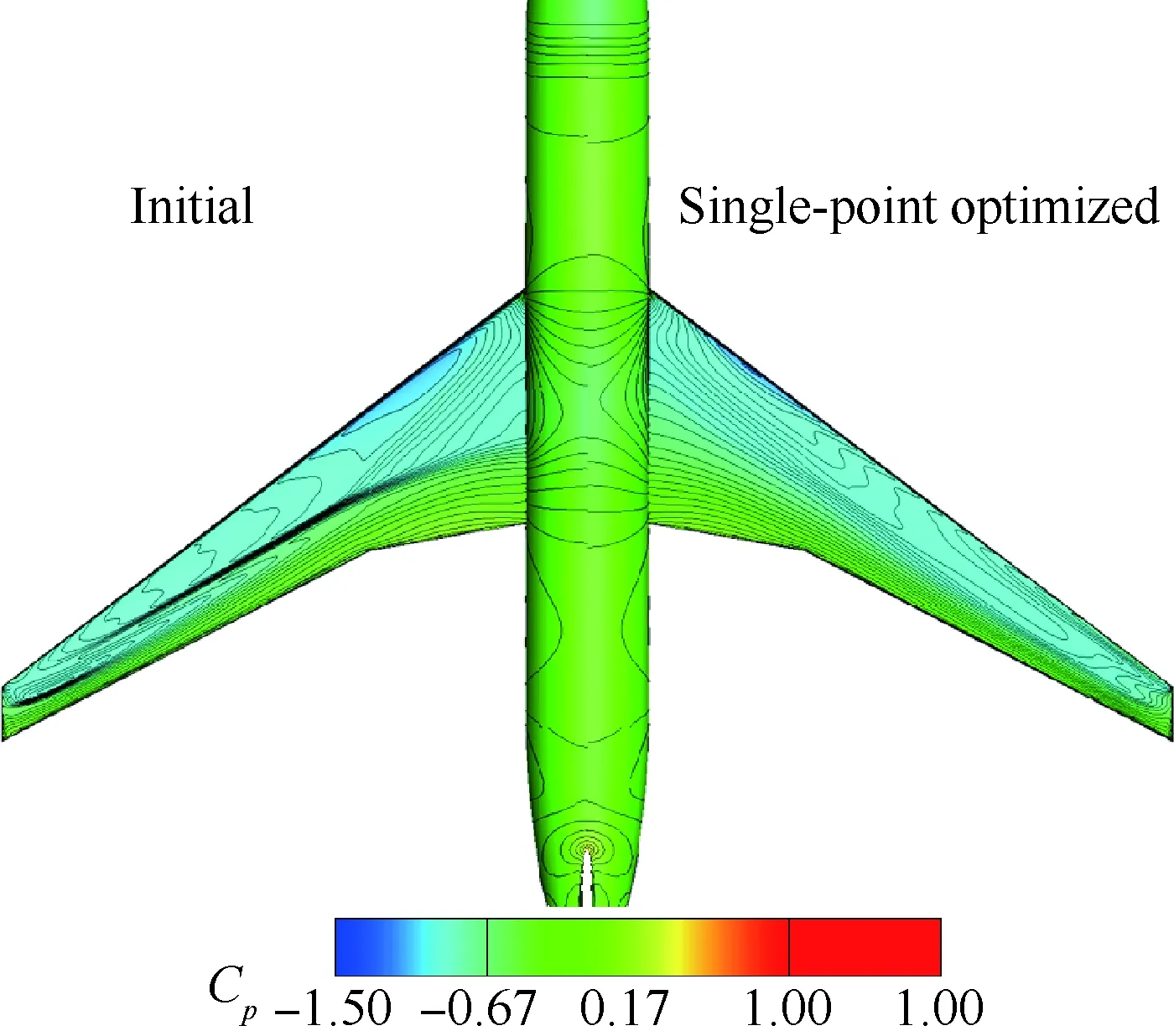
圖6 單點優化設計前后壓力云圖對比Fig.6 Comparison of pressure contour before and after single-point optimization configuration

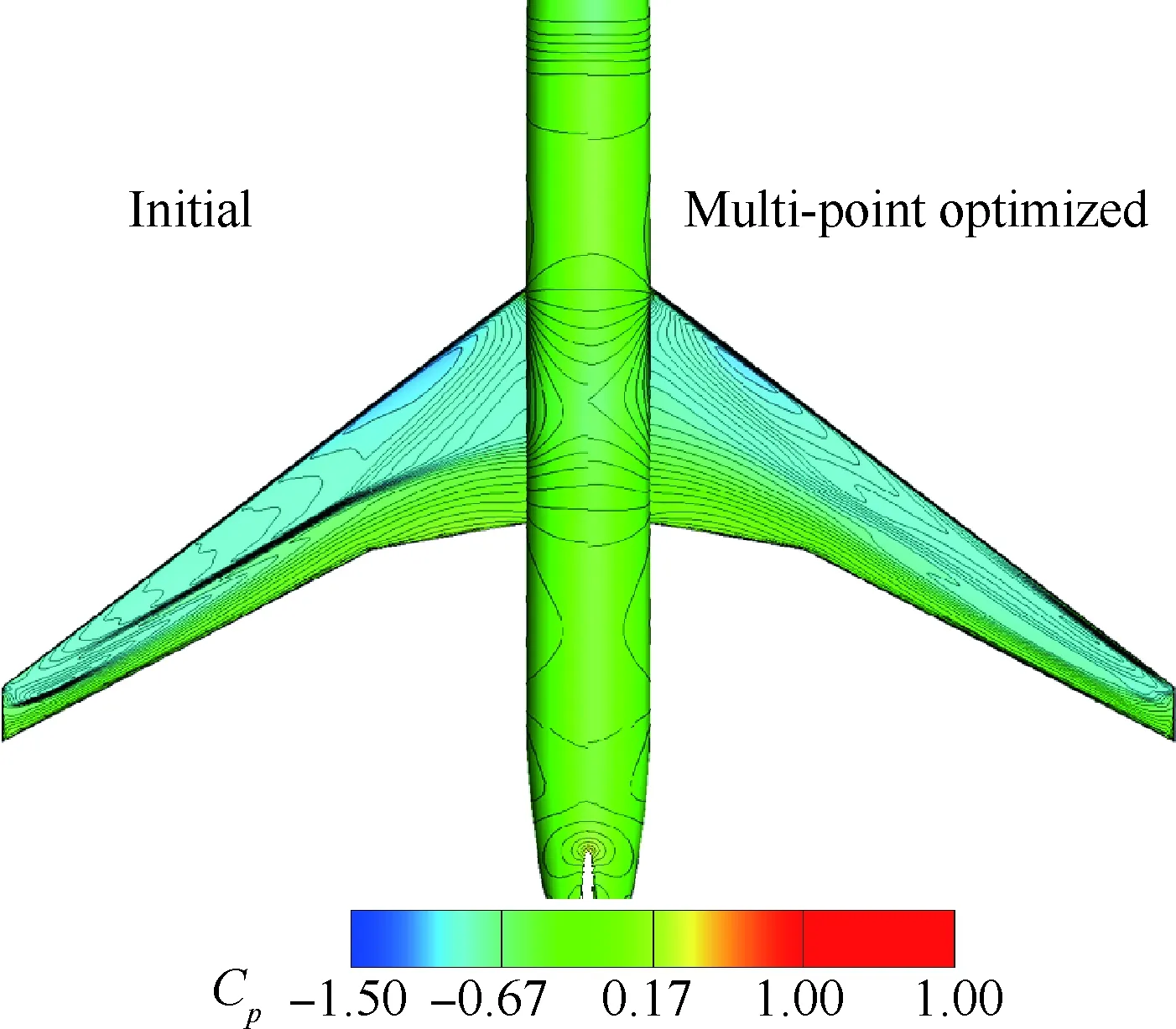
圖7 多點優化設計前后壓力云圖對比Fig.7 Comparison of pressure contour before and after multi-point optimization configuration

圖8 不同方法優化設計歷程Fig.8 Optimization design history of different methods

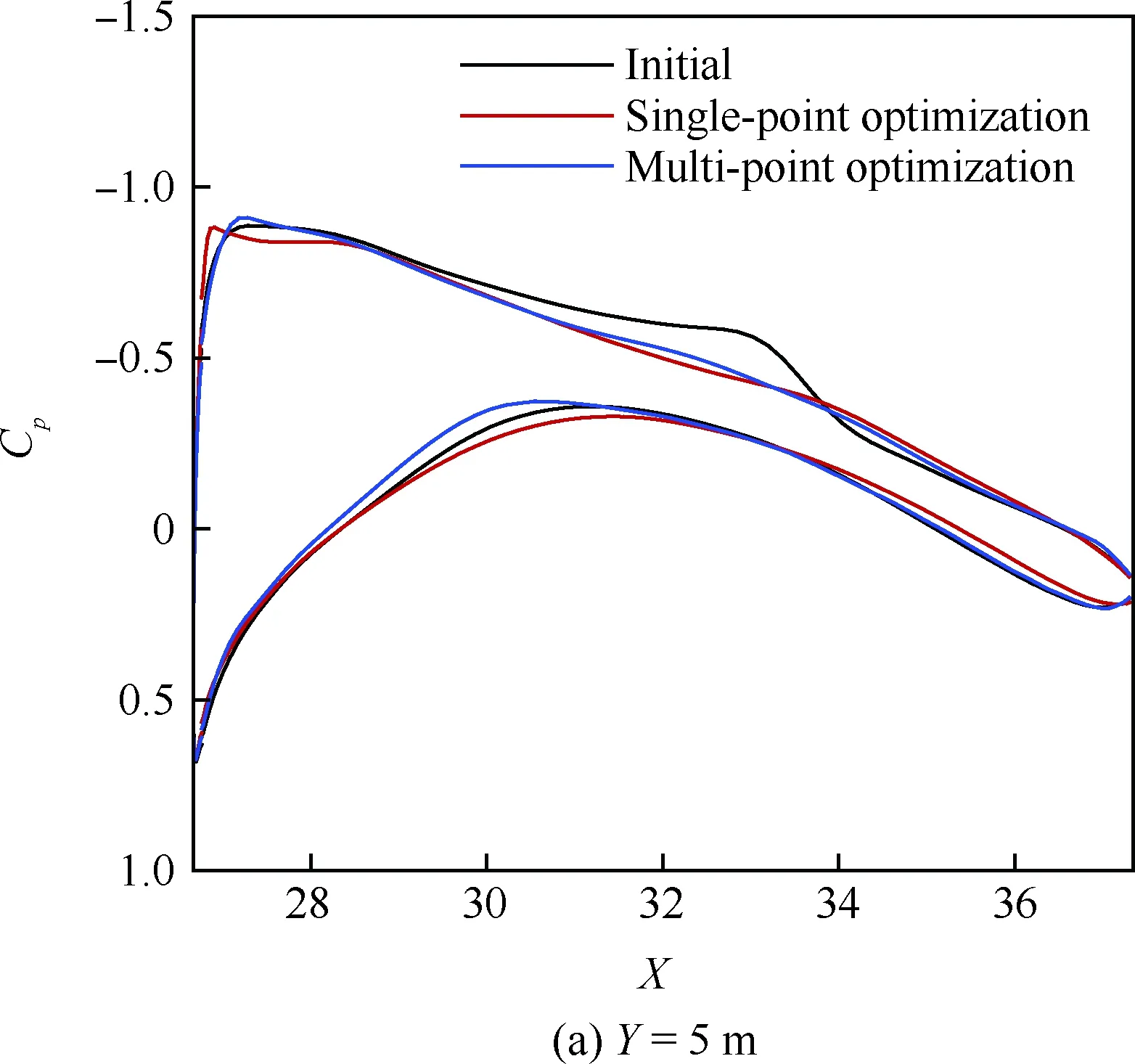
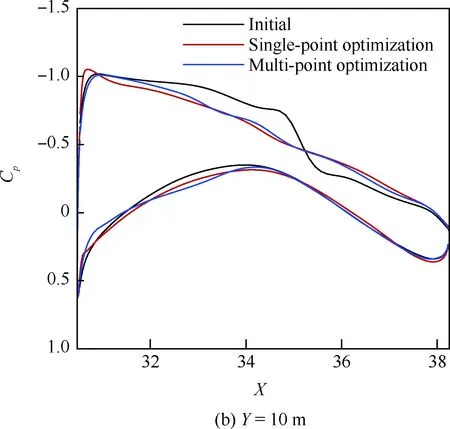
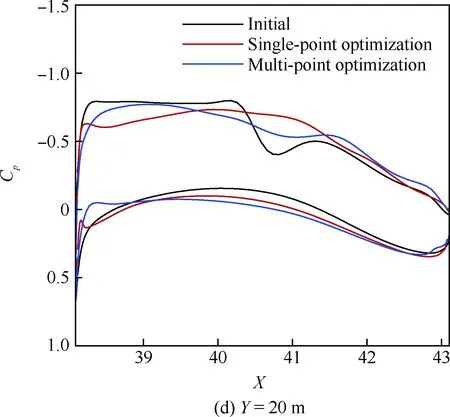
圖9 站位優化前后壓力分布對比Fig.9 Comparison of pressure distribution before and after station optimization

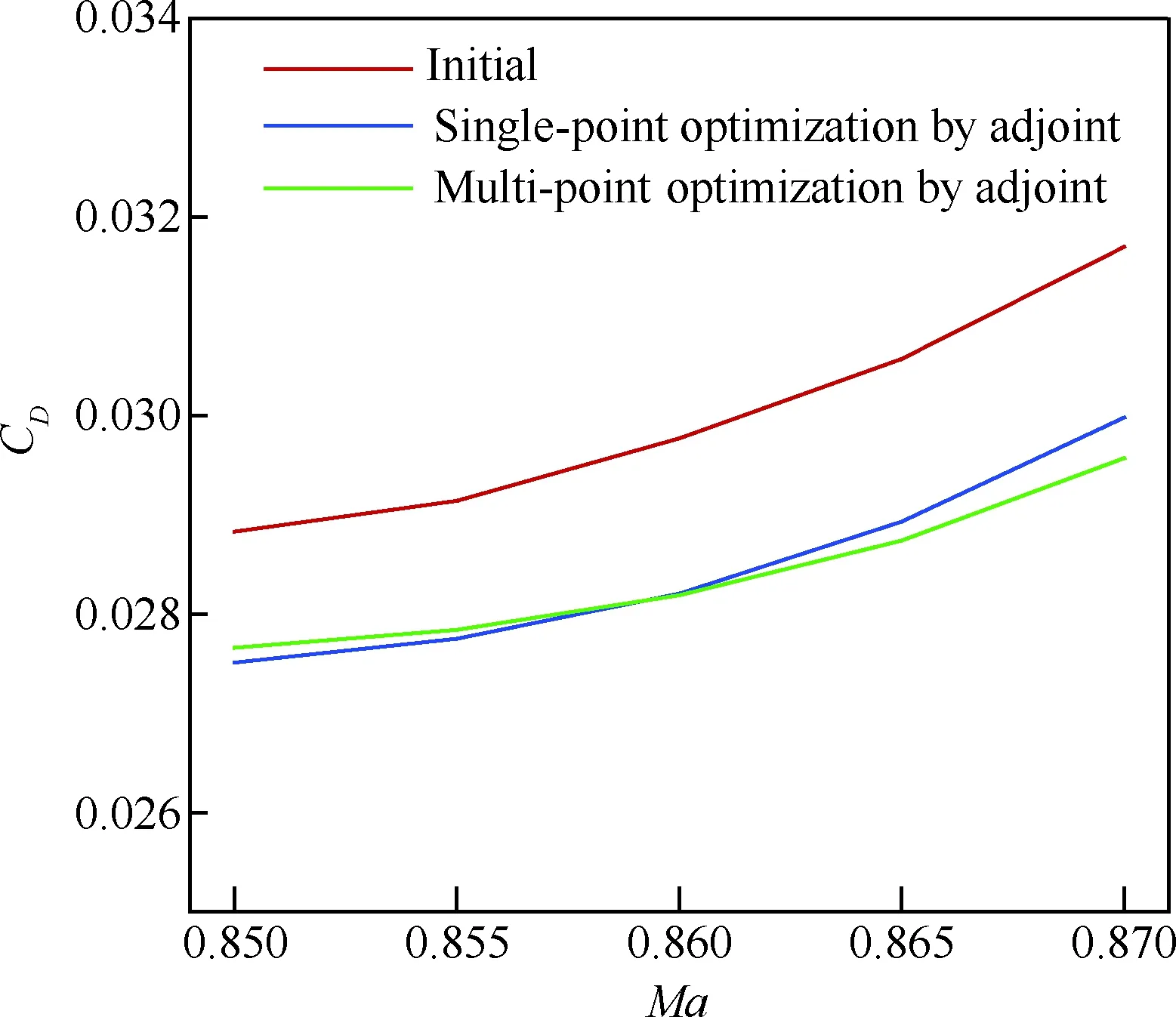
圖10 單點與多點設計阻力發散特性對比Fig.10 Comparison of drag divergence between single-point and multi-point designs

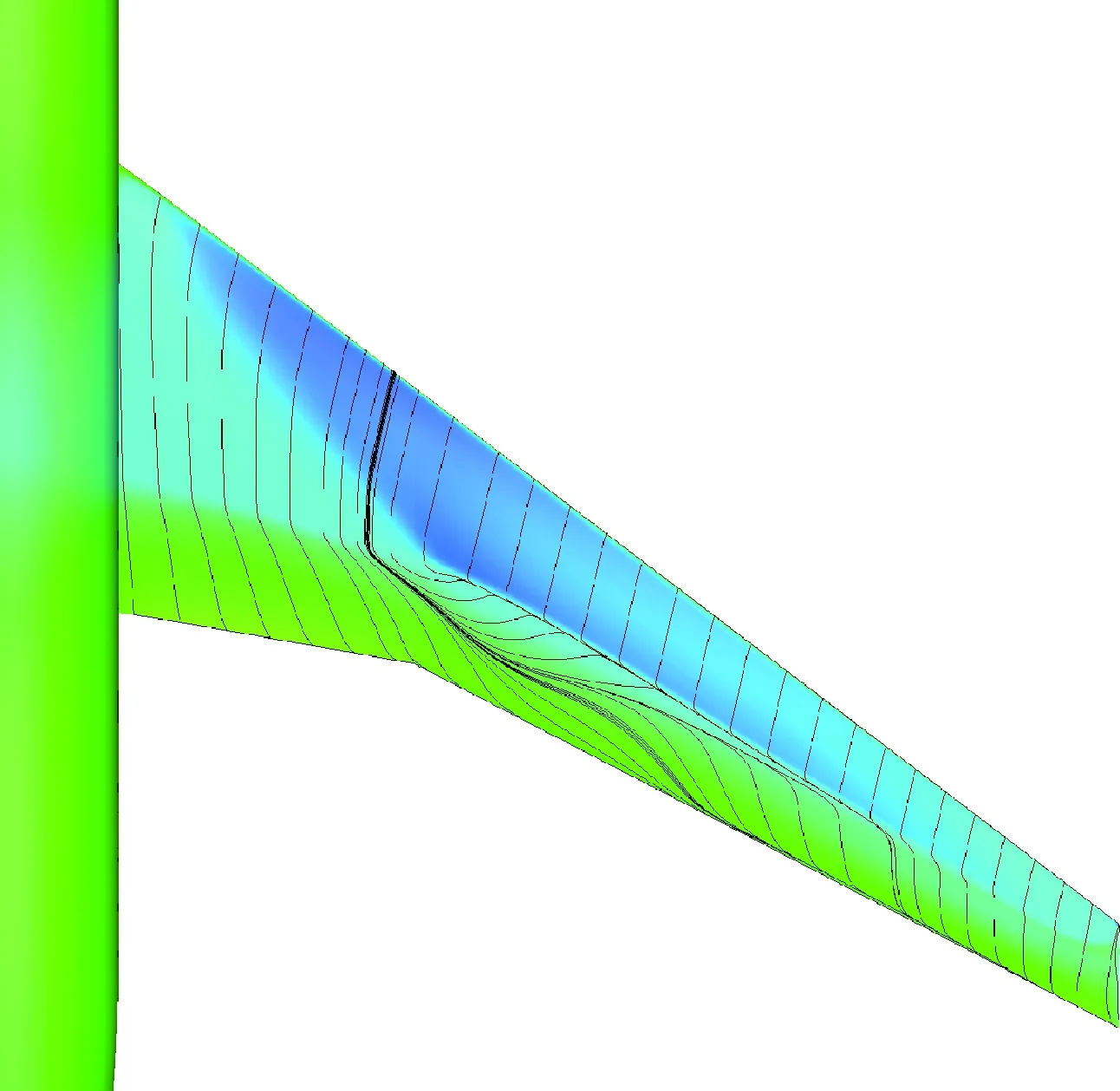
圖11 初始外形表面極限流線(CL=0.62)Fig.11 Limit streamlines of initial configuration surface (CL =0.62)

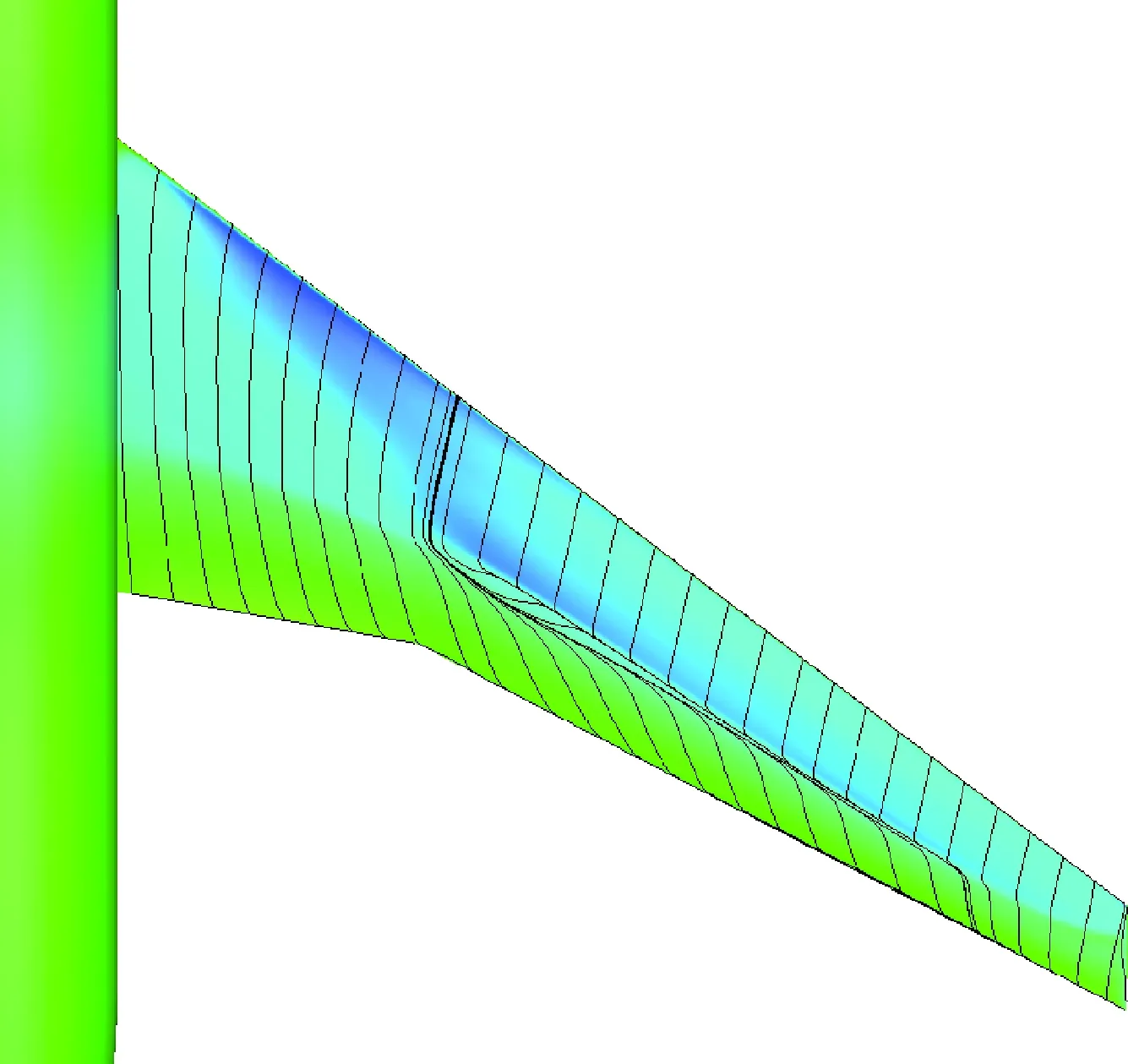
圖12 單點優化外形表面極限流線(CL =0.62)Fig.12 Limit streamlines of single-point optimized configuration surface (CL =0.62)

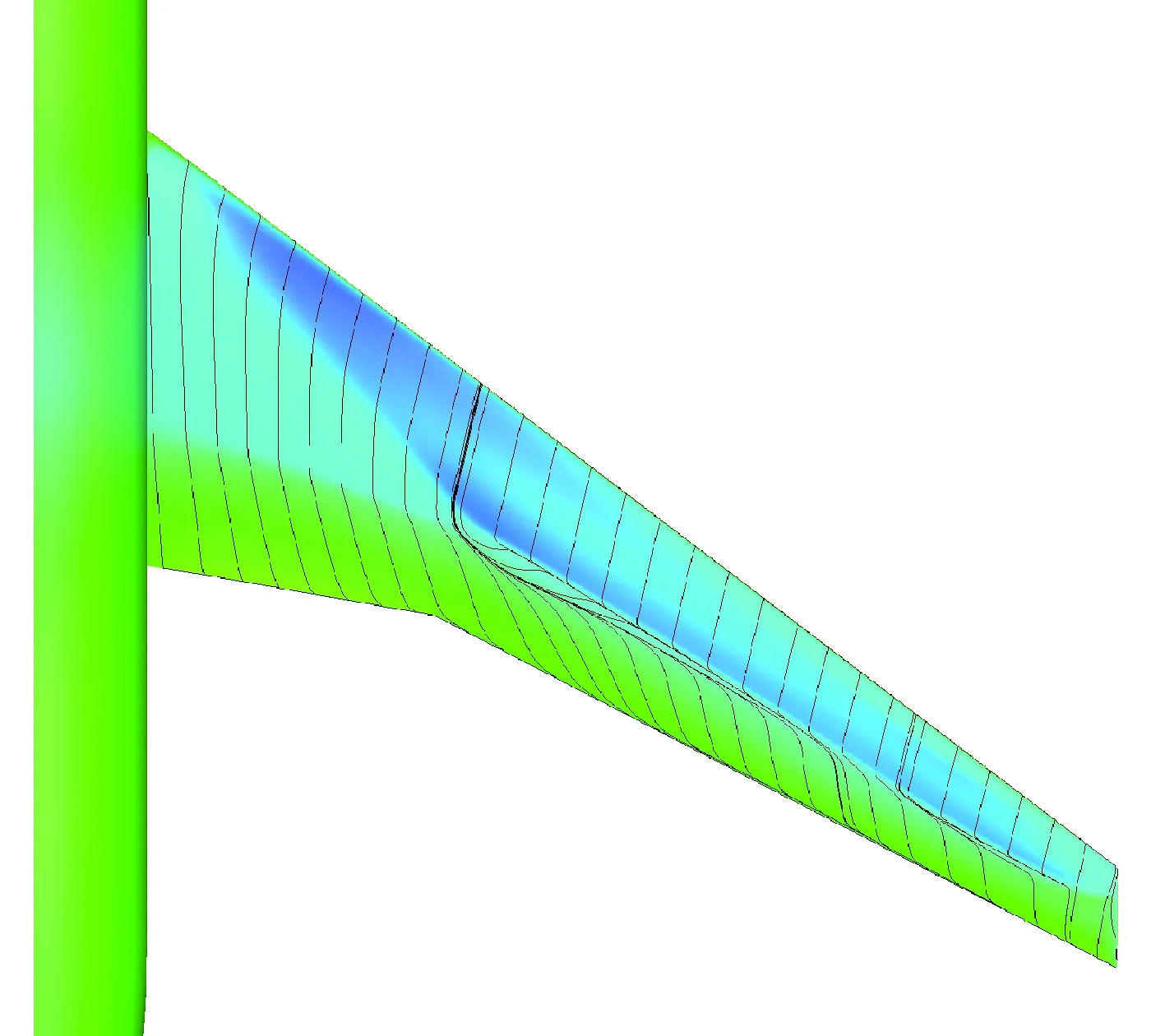
圖13 多點優化外形表面極限流線(CL=0.62)Fig.13 Limit streamlines of multi-point optimized configuration surface (CL =0.62)

5 “虛擬可行解”結合伴隨方法的進一步分析與討論

容易理解，對于各個目標函數均為單峰值的問題，加權疊加后，目標函數的峰值特性可能出現兩種情況，第一種，加權目標函數依然保持單峰值特性，另外一種，加權目標函數出現多峰值現象，這種依賴于具體問題，圖14和圖15給出了典型曲面函數疊加結果。

對于加權目標函數依然保持單峰值特性問題，盡管伴隨方法具有局部最優特性，仍然可以保持與進化算法優化結果的一致性；對于加權目標函數依然出現多峰值特性問題，優化伴隨方法的局部特性，“虛擬可行解”結合伴隨方法求解的虛擬Pareto前沿推進效果將劣于進化算法。

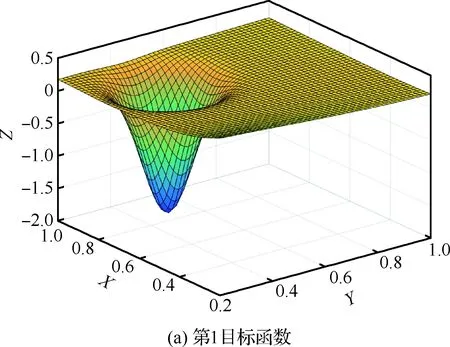
圖14 目標函數曲面Fig.14 Surface of object function

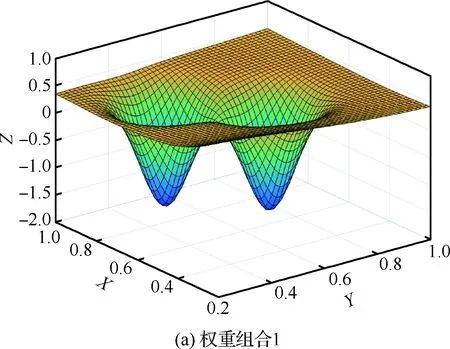
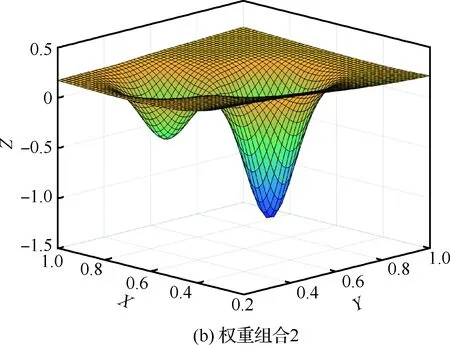
圖15 權重組合目標函數曲面Fig.15 Objective function surface of weight combination

該類情況同樣可以通過改變初始點的選擇從一定程度上消除疊加函數多峰值帶來的影響，而如何降低初始點選擇的盲目性，是基于伴隨理論與“虛擬可行解”方法在具體應用中值得關注的問題，這也是本文進一步的研究內容。在氣動設計中，目標函數加權組合均有可能出現單峰值或多峰值情況，且目標函數本身若是多峰值問題，加之高維設計空間因素，加權組合會出現更復雜的現象，設計結果依賴于初始點選擇，但對于工程型號設計問題來說，綜合分析策略不失為一種簡捷高效的優化設計方法，具有較強的工程應用價值。

6 結 論

1) 主分量分析可以有效分析出在一定的設計空間內不同目標函數的相關性，為目標空間有效降維提供參考。

2) 民用飛機構型單點、多點優化結果表明，相關性較強的目標函數特性均有所改善，驗證了主分量分析方法的有效性。

3) 多點設計外形的阻力發散特性、抖振特性得到了明顯改善，驗證了在主分量分析結果基礎上，“虛擬可行解方法”結合離散伴隨優化方法的有效性。

4) 阻力發散、抖振特性較好的氣動外形典型壓力分布形態呈現弱激波形態，壓力恢復位置較初始外形靠前，這與流動機理分析以及氣動設計經驗的認知較為一致。

5) 文中提出的綜合設計在不失主特征的前提下，提高多目標優化可視化水平。同時“虛擬可行解方法”結合離散伴隨優化方法能夠充分發揮兩種方法的優勢，實現高效多點設計。

盡管“虛擬可行解”結合伴隨方法優化的設計結果依賴于初始點的選擇(由于加權疊加目標函數存在多峰值特征的可能性)，但對于工程型號設計問題來說，不失為一種簡捷高效、具有工程應用價值的方法。如何進行初始點有效選擇，提高基于伴隨理論與“虛擬可行解”方法的優化設計品質、效率，是下一步的研究內容。