串聯型粘彈-粘塑性瀝青混合料本構模型的有限元分析

徐建平， 朱耀庭

(1. 重慶交通大學 土木工程學院，重慶 400074； 2. 江西省高速公路投資集團有限責任公司，江西 南昌 330025；3. 江西省交通科學研究院，江西 南昌 330038)

0 引 言

瀝青混合料的力學性能研究在道路工程中處于基礎性地位，對全面掌握瀝青路面結構行為具有重要作用。瀝青混合料是典型的粘、彈、塑性綜合體，其力學行為與加載速率、荷載時間以及溫度等因素密切相關[1]。

為能對瀝青路面結構進行更精確地應力應變分析，有必要對串聯型粘彈-粘塑性本構模型進行有限元實現。目前學界對瀝青混合料與時間的相關模型進行了研究與探討[2-7]，將與時間率相關模型植入有限元分析程序中，實現了瀝青路面結構有限元計算與分析。然而，對于瀝青混合料多階段串聯型粘彈-粘塑性本構模型的有限元實現還少見報道。

筆者針對目前瀝青混合料串聯型粘彈-粘塑性本構模型有限元實現方面的不足，在分析串聯型模型力學特性的基礎上，分別對粘彈、粘塑本構模型的增量離散化，采用數值穩定的徑向回退與向后歐拉積分方法[8-9]，并結合連續迭代R-M理論[10]，將編寫的材料本構模型子程序移植至有限元軟件ABAQUS中，從而實現了對瀝青混合料粘彈-粘塑性力學行為的數值模擬和分析。筆者通過建立隱式應力積分方程，并推導迭代所需的一致切線剛度矩陣，最后利用算例驗證了有限元實現的有效性。

1 粘彈性本構方程有限元

針對瀝青混合料的粘彈塑性力學特性，筆者在熱力學理論基礎上建立了串聯型粘彈-粘塑性本構模型，一維模型如圖1，本構方程如式(1)。利用室內試驗方法和數學計算對本構模型進行了參數獲取和敏感性評價[11]。

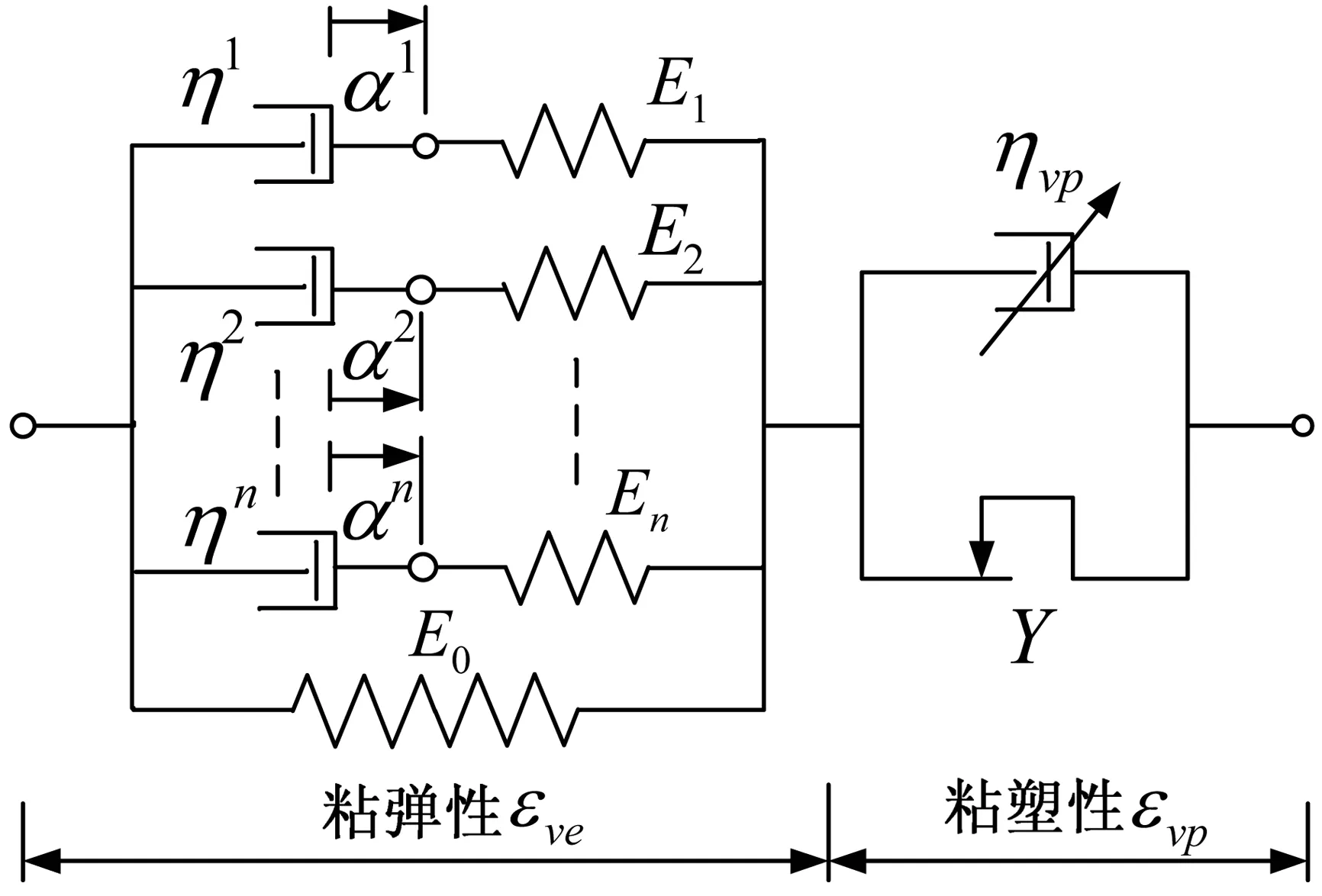
圖1 串聯型粘彈-粘塑性本構模型Fig. 1 Serial viscoelastic-viscoplastic constitutive model

(1)

式中：pr、lr、h、m、c、γ、q、b、β、s分別為粘彈-粘塑性材料常數。

根據Boltzmann線性疊加理論，可通過一個遺傳積分方程將各向同性粘彈性材料應力應變關系表示如式(2)[12]。

(2)

式中：σij(t)為應力張量；Sij(t)為偏應力張量；σkk(t)/3為應力張量第一不變量；Gijkl(t)為剪切松弛張量；Kijkl(t)為體積松弛張量；ekl為偏應變張量；εv為體積應變；上標符號表示為對時間的一次求導。

假定tr時刻應力狀態已知，將荷載作用時間劃為離散時間間隔為tr+1=tr+Δt，通過Prony級數性質表示廣義Maxwell模型力學特性，以此推導出遺傳積分應力增量在Prony級數條件下的表現形式如式(3)。

(3)

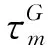
式(3)包含了彈性及粘性部分偏應力。對粘性部分積分進行單獨分析時，每個子模型粘性應變化可以通過式(4)來表示。

(4)

在時間增量為Δt條件下，式(4)變化可表示為式(5)：

(5)

由式(4)、(5)可得式(6)：

(6)

假定在時刻tr≤t≤tr+Δt內，粘彈性行為服從等應變率為Rε變化，如式(7)：

(7)

式(7)等號兩邊各減去tr時刻粘性應變，可得到粘性應變增量如式(8)：

(8)

則有式(9)：

(9)

同理可推導出體積應力增量，其表達式如式(10)：

(10)

上述遞推關系式可轉化為式(11)：

(11)

定義偏應力對偏應變的變化率為剪切切線模量GT，體積應力對體積應變的變化率為體積切線模量KT，法向應力增量可通過應力的體積增量和偏增量進行表示，得出GT和KT表達式如式(12)：

(12)

在有限元計算中，還需推導一致切線剛度矩陣，根據Jacobian矩陣的定義[13]可得出如式(13)：

(13)

2 粘塑性本構方程有限元

由于粘塑性本構模型方程是用時間導數微分方程表示，如何利用精確和有效的數學算法對模型方程進行積分運算，是有限元實現過程中遇到的最大困難。有限元計算采用等參單元，對本構模型方程積分過程是通過高斯點計算來實現，而更新的材料參數為應力和粘塑性兩個變量。所采用數值算法必須滿足以下4個基本條件[14]：① 被積分后的表達方程與粘塑性本構方程相一致；② 數值方法是穩定的；③ 粘塑性增量是一致的；④ 具備二階精確度。因此，隱式積分算法可保證應力結果準確性，能滿足上述基本條件，筆者將在向后歐拉積分算法基礎上，建立粘塑性本構方程的一致切線算子。

2.1 本構方程的離散化和返回映射

粘塑性本構模型采用一組微分方程和其初值條件進行表述，微分方程組由應變增量通過積分離散計算進行實現，由于向后歐拉方法具有數值有效性和絕對收斂性，因而被廣泛應用于(粘)塑性有限元數值計算中[15-16]。采用后退歐拉積分的方法將粘塑性本構方程離散，并對硬化方程進行表述，方程離散后表示如式(14)：

(14)

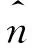
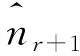
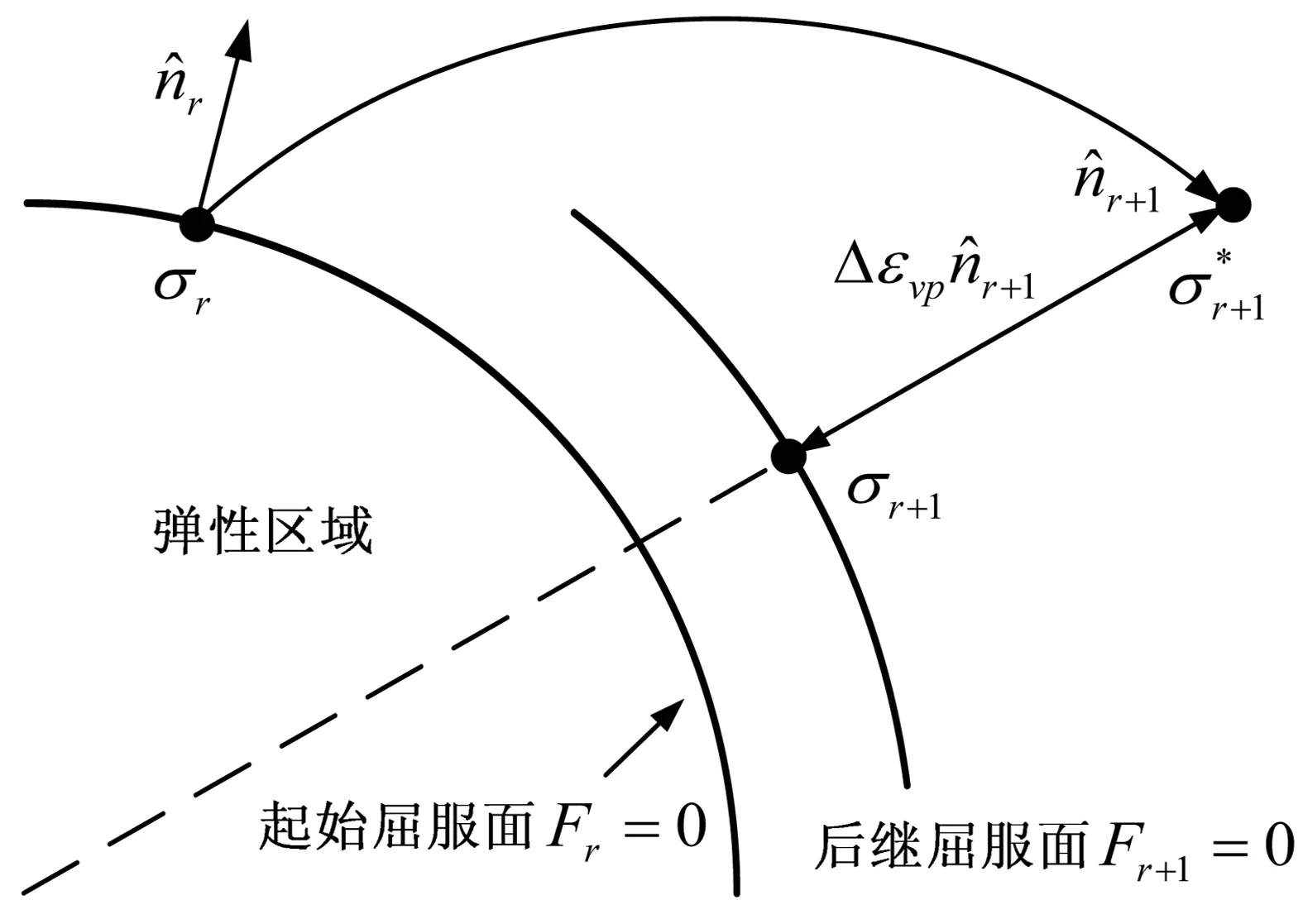
圖2 徑向回退法幾何闡述Fig. 2 Geometrical view of the radial regression method

若tr時刻σij(tr)、εij(tr)、εvpij(tr)、Xij(tr)等力學狀態變量均為已知，通過給定Δεij(tr+1)和Δt，則可采用彈性預估-塑性校正方法求出tr+1時刻的各個變量。假設給定的應變增量Δεij(tr+1)全部為彈性應變，則引入彈性嘗試應力如式(15)：

(15)

式中：Cijkl為彈性模量4階張量。

此時，屈服準則由彈性嘗試應力改為式(16)：

(16)

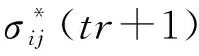
(17)

式中：CijklΔεvpkl(tr+1)稱為粘塑性校正項。

由此可見，只需求得εvpkl(tr+1)，則σij(tr+1)等變量將容易獲得。

假定粘塑性材料各向同性，且塑性不可壓縮，則粘塑性校正項偏量可通過材料剪切模型進行表示，如式(18)：

(18)

則由式(18)可得式(19)：

(19)

則得出有效應力第2不變量如式(20)：

R[ΔP(tr+1)]

(20)

式(20)可表示為累計粘塑性應變ΔP(tr+1)的方程，對有效應力第2不變量進行表示如式(21)：

(21)

式(20)和式(21)得到一個關于ΔP(tr+1)的非線性方程，如式(22)：

(22)

當ΔP(tr+1)求解得出后，則可求解出時間子步條件下各變量增量，從而得出各變量。值得指出的是，式(22)為一非線性方程組，可采用N-R迭代方法對未知變量進行求解，計算流程如圖3。

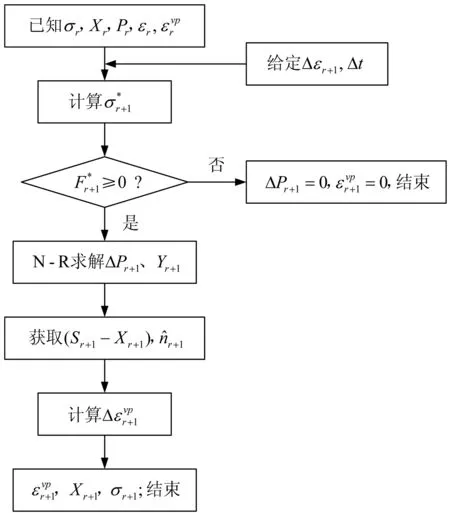
圖3 N-R迭代算法流程Fig. 3 N-R iterative algorithmic process

2.2 一致切線算子

有限元程序在計算積分過程中，在時間增量結束時，一致切線剛度矩陣d△σij/d△εij用于表示應變增量的無窮小變化情況下的應力分量變化。對式(14)進行微分推導，可得Jacobican行列式如式(23)：

(23)

3 串聯型粘彈-粘塑性模型有限元

串聯型粘彈-粘塑性本構模型有限元計算與彈塑性材料相類似，計算之初需要判斷材料是否已經進入屈服階段，在未進入屈服之前只表現為粘彈性行為，而進入屈服階段以后則表現為粘彈性和粘塑性的共同響應，應變則表現為粘彈性與粘塑性應變之和。因此，串聯型粘彈-粘塑性模型的有限元計算本質上和粘彈性或粘塑性分析本質上時相同的，需根據屈服法則對各個有限元單元做出屈服判斷，然后按不同應力應變狀態做出相應的判定和計算處理。對于已進入屈服的有限元單元采用粘塑性計算方法，對未進入屈服的有限元單元則采用粘彈性方法進行分析。其有限元計算流程如圖4。

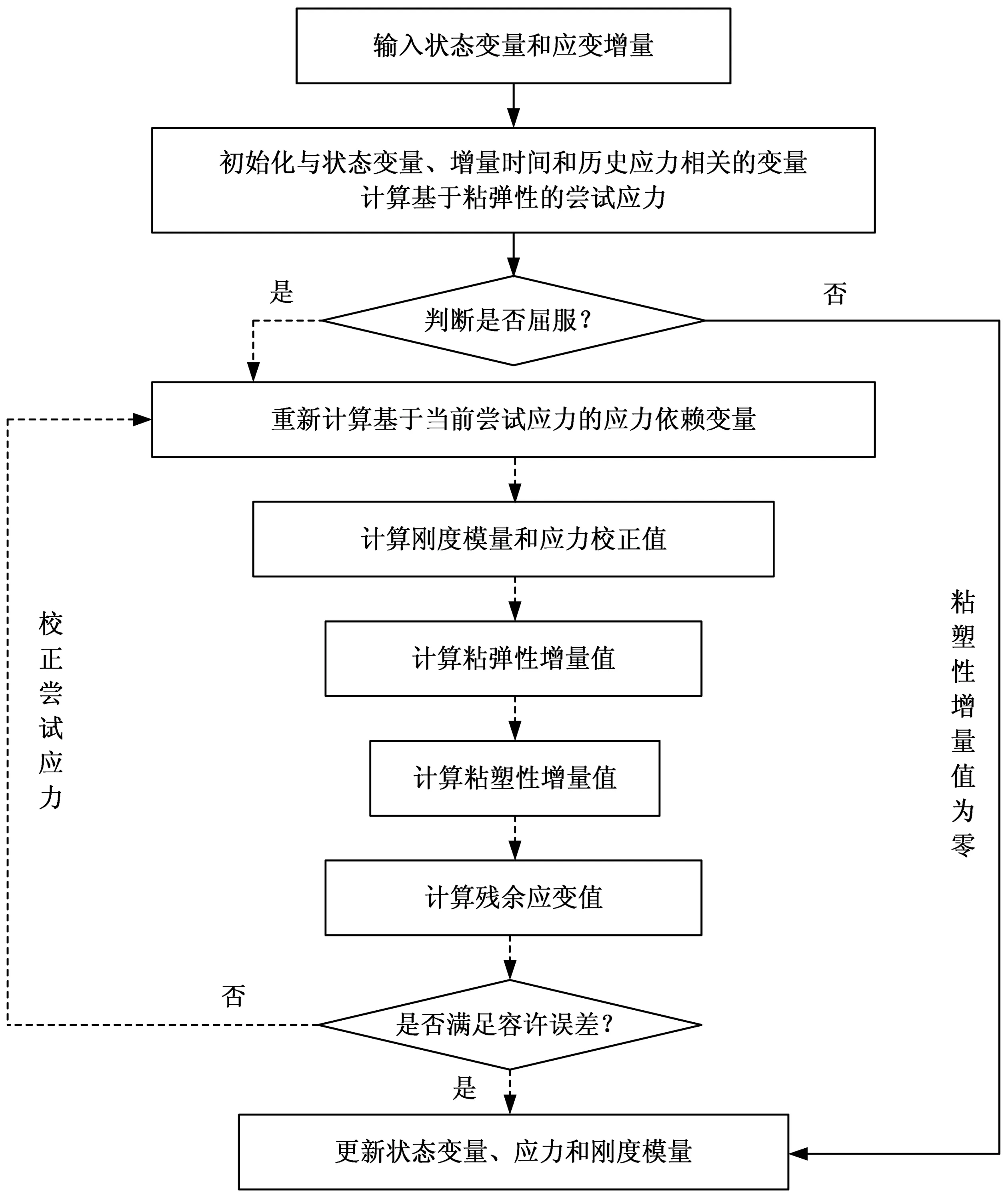
圖4 串聯型粘彈-粘塑性有限元計算流程Fig. 4 The calculation process of serial viscoelastic-viscoplastic finite element model

4 數值驗證

筆者利用ABAQUS有限元平臺進行有限元用戶材料(UMAT)子程序的二次開發和編程[18]。通過對室內實驗進行模擬，計算結果與實驗數據對比，以驗證數值實現的準確性。由于文中所涉及本構模型為串聯型，要準確獲取材料模型參數要將粘彈性和粘塑性進行解耦和分離，對材料行為時間相關性進行分配，基于此提出的策略為：通過小應力幅值動態試驗獲取粘彈性材料參數，利用靜態蠕變試驗對粘彈性和粘塑性解耦獲取粘塑性力學行為，結合本構模型特征編制數據擬合程序，得出粘塑性模型參數，具體模型參數和實驗數據請見文獻[2]。

瀝青混合料動態模量和靜態蠕變室內試驗采用的是圓柱形試件，試件高度為150 mm，直徑為100 mm。試件幾何尺寸、荷載和邊界條件均軸對稱，可采用軸對稱單元模型以簡化為二維模型進行計算，但筆者編制的UMAT子程序仍考慮到了三維狀態條件。

建模中，有限元模型尺寸和試件相同，剛體模擬加載壓頭和支撐底座。有限元模型網格劃分通過剖分和掃掠方法得到圓心向圓周發散的三維網格，單元類型為20結點減縮積分單元C3D20R。在實際的試驗過程中，對試件底面并沒有進行約束，同時由于實驗過程采用雙層乳膠膜以保障試件端面的自由變形，只進行了Z方向約束，即U3=0。試件頂面為在施加均布應力的加載方式。

4.1 粘彈性結果

粘彈性材料響應的表征可體現為蠕變和應力松弛，由于瀝青混合料材料的特殊性，一般室內對粘彈性采用蠕變實驗獲取蠕變應變或柔度，再通過蠕變和松弛之間的粘彈性關系，可計算出松弛應力或模量[19]。計算結果如圖5。

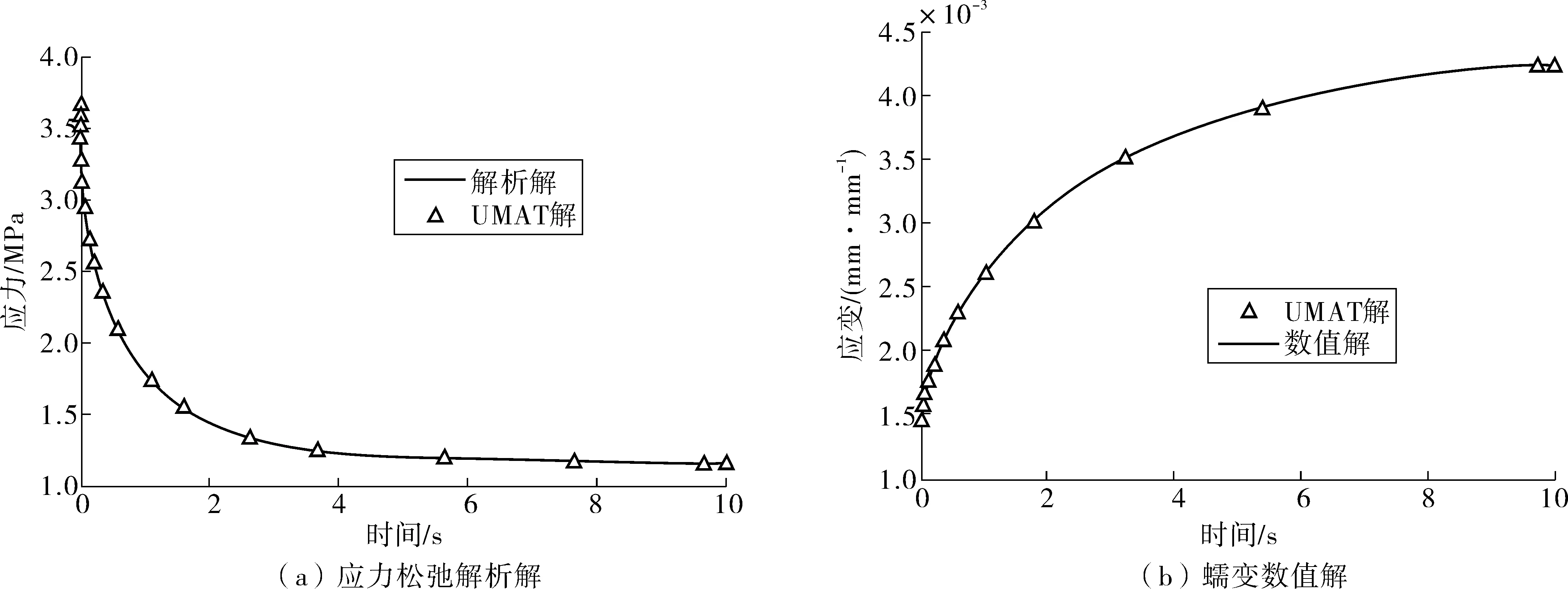
圖5 應力松弛解析解和蠕變數值解與UMAT計算對比Fig. 5 Comparison between analytical solution of stress relaxation and numerical solution of creep and UMAT calculation

由松弛和蠕變計算結果可看出：粘彈性UMAT應力松弛計算解和解析解基本上相同，結果幾乎無差別，而蠕變有限元解和數值解也基本上相同，表明有限元子程序有非常好的準確性。

4.2 粘塑性結果

粘塑性本構方程由一組隱形方程組構成，無法直接得出解析解，通過文獻[2]中改進的有限差分格式可獲取本構方程的數值曲線，本節采用蠕變模擬進行差分解和有限元解的對比分析。同時，由于粘塑性需要采用達到屈服條件才可驗證，模擬加載應力需大于材料的粘塑性屈服應力。不同條件蠕變計算結果如圖6。

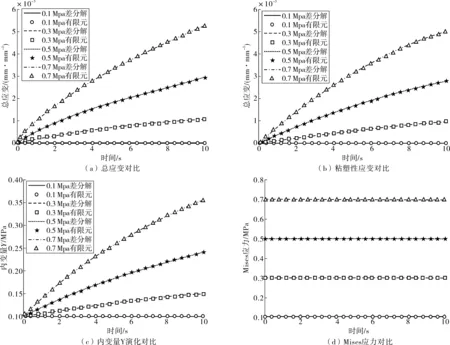
圖6 有限元計算和改進差分法計算結果對比Fig. 6 Comparison between the calculation results of finite element calculation and the improved difference method

由蠕變實驗模擬和計算結果對比可知，粘塑性子程序是準確和可靠的，能正確地反映出粘塑性材料的力學響應和內變量的發展趨勢。

4.3 串聯型粘彈-粘塑性結果

串聯型粘彈-粘塑性材料的有限元計算之初要判定材料是否已進入屈服階段，在未進入屈服以前只表現為粘彈性行為，進入屈服以后則表現為粘彈性及粘塑性共同響應。因此，串聯型粘彈-粘塑性計算結果驗證分為兩個階段，一個為材料未達到屈服狀態；另一個為材料進入屈服狀態而發生了粘塑性變形。未進入屈服和進入屈服狀態的模擬結果如圖7、8。

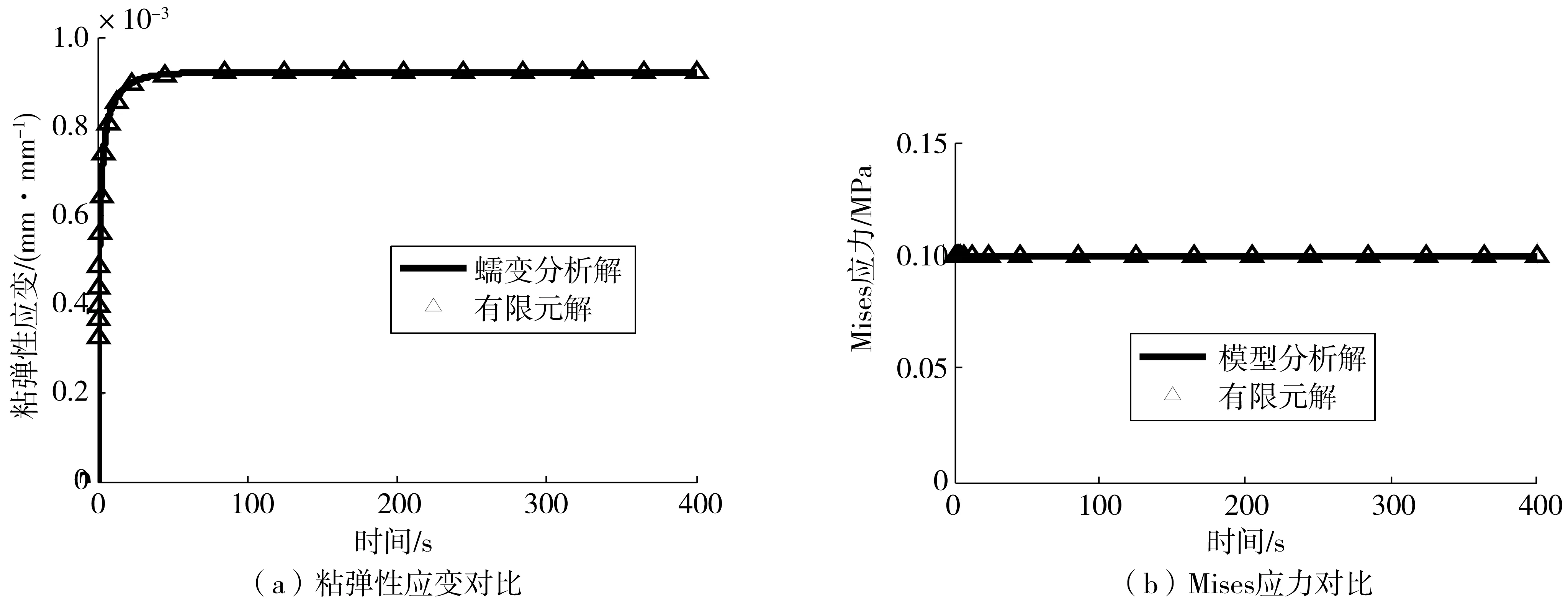
圖7 未達屈服條件下計算結果對比Fig. 7 Comparison of calculation results under non-yield conditions

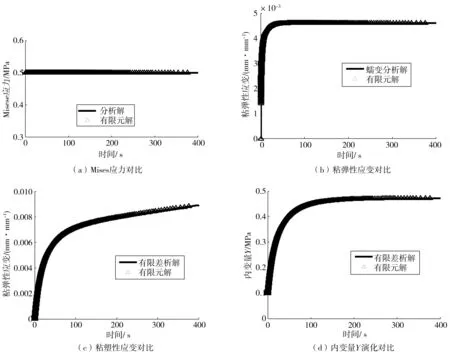
圖8 屈服條件下計算結果對比Fig. 8 Comparison of calculation results under yield condition

由圖7、8可見：無論屈服狀態還是未達屈服狀態，計算結果和理論分析都具有很好一致性，串聯型粘彈-粘塑性本構模型有限元實現是有效的，能準確反映出瀝青混合料與時間相關力學行為發展和演化規律。

5 結 論

筆者以瀝青混合料與時間相關本構模型為研究對象，通過編制用戶子程序，對串聯型粘彈-粘塑性模型進行了有限元分析，通過瀝青混合料試件在典型室內試驗條件力學行為進行了有限元模擬和室內試驗數據的對比，驗證了筆者提出方法的正確性和可靠性，并得出以下結論：

1)串聯型本構模型的有限元可依據模型特點表示為粘彈性和粘塑性兩部分的應力相同而應變相加；

2)通過遞推關系得出粘彈性、粘塑性本構模型的離散化方程，數值解和解析解進行對比，其結果基本一致，驗證了文中模型離散化法有效性；

3)粘塑性模型采用徑向回退與向后歐拉積分方法，并結合連續迭代R-M法可有效地解決模型離散化非線性方程組計算過程的穩定性和收斂問題；

4)當將串聯型模型用于瀝青路面結構計算中，只需將瀝青結構層材料定義為模型屬性即可快速實現路面結構永久變形計算和分析。