企業R&D投入與產學研協同創新績效分析

李 鵬，李美娟，陳維花

（福州大學 經濟與管理學院，福州 350116）

0 引言

“創新、協調、綠色、開放、共享”五大發展理念在黨的十八屆五中全會中被提出，其中，被擺在國家發展全局核心位置的發展理念是創新。由于企業的可持續發展離不開創新，創新問題一直是學者們研究的熱點。Wakelin[1]采用Cobb-Douglas生產函數研究企業的R&D支出與生產率增長的關系，發現R&D支出對生產率增長具有顯著的影響。嚴焰等[2]運用分組回歸方法，發現企業R&D投入對創新績效有正向促進作用。高楠[3]利用灰色關聯度方法，計算企業R&D投入與創新績效的灰色關聯度，結果和嚴焰等[2]一樣，兩者正相關。何慶豐等[4]通過主成分分析法等方法，實證分析R&D投入與創新績效間的定量關系，發現R&D投入對創新績效的貢獻為正。

國內外學者們根據自己的研究內容和目的，運用不同的方法分析了企業R&D投入與創新績效的關系，但很少使用面板數據模型來分析。本文利用2009—2015年全國30個省份的面板數據，運用多指標面板數據因子分析方法對企業R&D投入多指標進行縮減，然后進行單位根檢驗和協整檢驗，最后采取面板數據模型分析了企業R&D投入與產學研協同創新效果的關系。

1 模型的設定

作為產學研協同創新的核心利益相關者之一，企業對產學研協同創新發展起著不可或缺的作用，其中R&D投入對創新績效的作用往往具有決定性意義。企業需要不斷加強核心競爭力，提高對R&D投入，增強企業的活力，促進企業可持續健康發展。

根據相關文獻，企業R&D投入主要由企業R&D人員和企業R&D經費組成[5]。本文采用面板數據模型實證分析企業R&D投入對創新績效的影響作用。選取“規模以上工業企業R&D經費投入”“規模以上工業企業R&D人員投入”“規模以上工業企業R&D項目數”作為衡量企業R&D投入的指標。將產學研協同創新績效分為創新經濟績效和創新科技績效，分別選擇“新產品銷售收入”和“專利授權數”作為其替代變量。“新產品銷售收入”不僅從經濟效果方面反映了創新績效的情況，而且能夠代表創新成果的轉化能力，反映創新經濟績效；“專利授權數”代表的是產學研協同創新產出成果的實際結果，可以用來反映創新科技績效。這兩個指標的數值越高，說明企業創新成果轉化率越好。本文的相關初始數據均來自《中國統計年鑒》和《中國科技統計年鑒》的歷年數據。

模型具體設定如下：

其中，y1表示創新經濟績效，y2表示創新科技績效；下標i和t表示第i個省份第t期的相應指標；X4表示企業R&D投入，使用多指標面板數據因子分析方法計算得來，其系數β反映了企業R&D投入對創新經濟績效和創新科技績效的影響效果；υ是隨機擾動項，滿足E(υ)=0和var(υ)=σ2。

2 實證分析

2.1 多指標面板數據因子分析

為了方便、直觀地分析企業R&D投入對產學研協同創新績效的影響，本文將“規模以上工業企業R&D經費投入”“規模以上工業企業R&D人員投入”“規模以上工業企業R&D項目數”多個指標因子分析降維成一個變量。使用多指標面板數據因子分析方法，即將面板數據各個時間截面數據按時間順序平鋪展開形成一個大截面數據。使用軟件SPSS 18.0來輔助完成分析。

對初始數據進行標準化處理，減少因數據間的單位存在量綱差異而可能導致的不必要誤差，接著對處理好的數據進行因子分析適用性檢驗，如表1所示。

表1 適用性檢驗結果

為了確定所選指標是否適合進行因子分析，可通過表1的KMO值和Bartlett檢驗的概率值來分析。可以看到，KMO值為0.771，Bartlett檢驗的概率值為0.000，均說明本文選取的指標適合進行因子分析，可以進一步進行數據分析。

表2是運用主成分分析法提取因子并選取大于1的特征根的分析結果。可以看到，只需要1個特征根就可以解釋我國30個省份企業R&D投入情況的97.075%。說明選取的3個初始指標表達的信息可以縮減至1個綜合指標，并能很好地反映因子分析降維的思想。

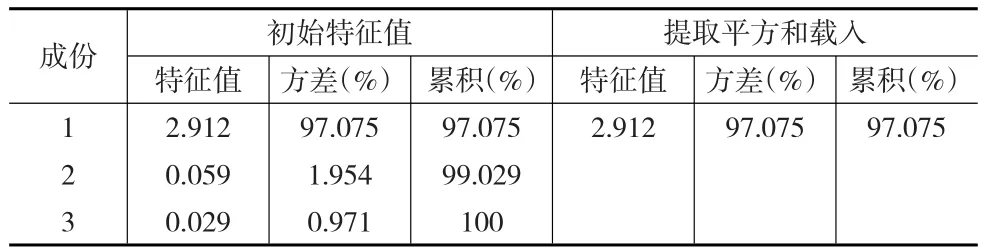
表2 解釋的總方差情況

一般情況下，需要確定各指標的權重。按照加權平均的方法，求出綜合得分。由于只提取了1個公因子，這個公因子上的得分就是所求的綜合得分，計算公式為：

其中，φi（i=1，2，3）為因子得分系數；X1、X2、X3使用原始數據，這與楊俊等[6]處理方法一樣。企業R&D投入成份得分系數矩陣如表3所示。

表3 企業R&D投入成份得分系數矩陣

2.2 單位根檢驗與協整檢驗

在對變量進行回歸數據分析之前，為了防止虛假回歸，保證變量平穩性，先對面板數據進行單位根檢驗。常用的方法主要包括假設樣本單位根一致和假設樣本單位根不一致兩種情況，前者主要方式有LLC、Hadri和Breitung，后者主要方式有IMP、IPS、Fisher-ADF和Fisher-PP。一般情況下，若面板數據是平穩的，需要拒絕存在單位根的原假設。

分別對面板數據lny1、lny2和lnX4進行單位根檢驗，采用Eviews8.0軟件，檢驗結果如表4所示。可以看出，lny1、lny2和lnX4均在1%的顯著水平下是平穩的，均存在單位根，即lny1、lny2和lnX4均為一階單整變量。

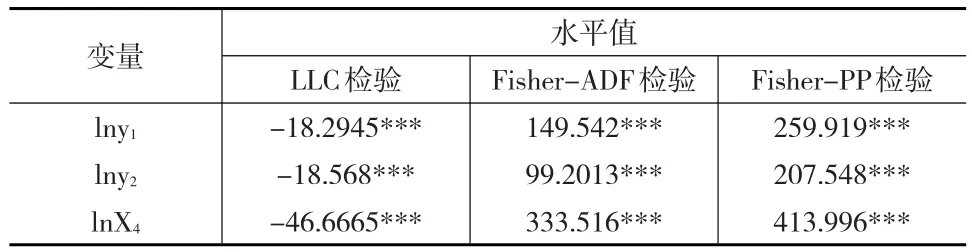
表4 面板單位根檢驗結果

同樣的，需對面板數據進行協整檢驗，常用的方法主要以Engle and Granger二步法檢驗為基礎和以Johansen協整檢驗為基礎。前者主要方式有Pedroni和Kao，Pedroni允許面板數據存在異質性，其構造了7個檢驗面板協整的統 計 量 ：Panel-v、Panel-rho、Panel-PP、Panel-ADF、Group-rho、Group-PP和Group-ADF。其中，前4個用聯合組內維度描述，后3個用組間維度描述的。本文采用Pedroni檢驗，lny1、lnX4和lny2、lnX4的面板協整檢驗結果如表5所示。

表5 Pedroni面板協整檢驗結果

根據Pedroni[7]的研究結論，本文參考Panel-PP、Panel-ADF、Group-PP和Group-ADF四個統計量的結果。從表5檢驗結果看，可以認為企業R&D投入與創新經濟績效和創新科技績效之間均存在長期的均衡關系。

2.3 回歸結果分析

在確定采用哪一種具體模型進行數據分析之前，能夠采用的方法有F檢驗和Hausman檢驗。本文采用Hausman檢驗，同樣運用Eviews 8.0軟件輔助，檢驗結果表明P值遠小于顯著性水平0.05，所以本文采用固定效應模型（排除隨機效應模型和混合效應模型）來分析企業R&D投入對產學研協同創新績效的影響。

下頁表6是對模型（1）和模型（2）參數進行回歸的結果果。可以看出，調整R2值分別為0.995、0.992，說明兩個模型的擬合優度很高；F的值均在1%水平下顯著，說明兩個模型總體線性關系顯著。

從表6可以得出：（1）除了吉林和黑龍江之外，全國其他地區企業R&D投入X4的系數均能通過t檢驗，表明企業R&D投入對產學研協同創新經濟績效的影響顯著；企業R&D投入的彈性系數平均水平為0.981，說明了企業R&D投入對創新經濟績效具有積極的促進作用。（2）企業R&D投入對產學研協同創新經濟績效影響最大的是江西，其彈性系數約為1.526，說明該省創新經濟績效受企業R&D投入的影響較大；除江西之外，企業R&D投入的彈性系數較大的省份有浙江、新疆、海南、河南、江蘇、湖南、寧夏、安徽、河北、湖北、廣東、甘肅，彈性系數都在0.981以上，說明這些省份的企業R&D行為對創新經濟績效有較好的促進作用。（3）青海的企業R&D投入對產學研協同創新經濟績效的影響最小，其彈性系數約為-2.234，相對于其他省份，青海省企業R&D行為的增加并未推動創新績效的提高。青海省2015年R&D人員全時當量僅為4008人年，是除西藏外全國30個省份中最少的，而R&D人員全時當量最高的是廣東，為501696人年，是青海的125多倍。科技人才的欠缺在很大程度上削弱了青海的技術創新能力與創新績效實力。除青海之外，陜西、黑龍江、吉林三省的企業R&D行為的彈性系數也比較小，都在0.5以下，說明這4個省份的企業R&D行為對產學研協同創新經濟績效的促進作用弱于全國其他地區。（4）北京、遼寧、天津、福建、山西、山東、貴州、廣西、云南、上海、重慶、四川和內蒙古這13個省份的企業R&D行為對產學研協同創新經濟績效的影響在全國位于中等水平，彈性系數都在0.5～0.981之間。

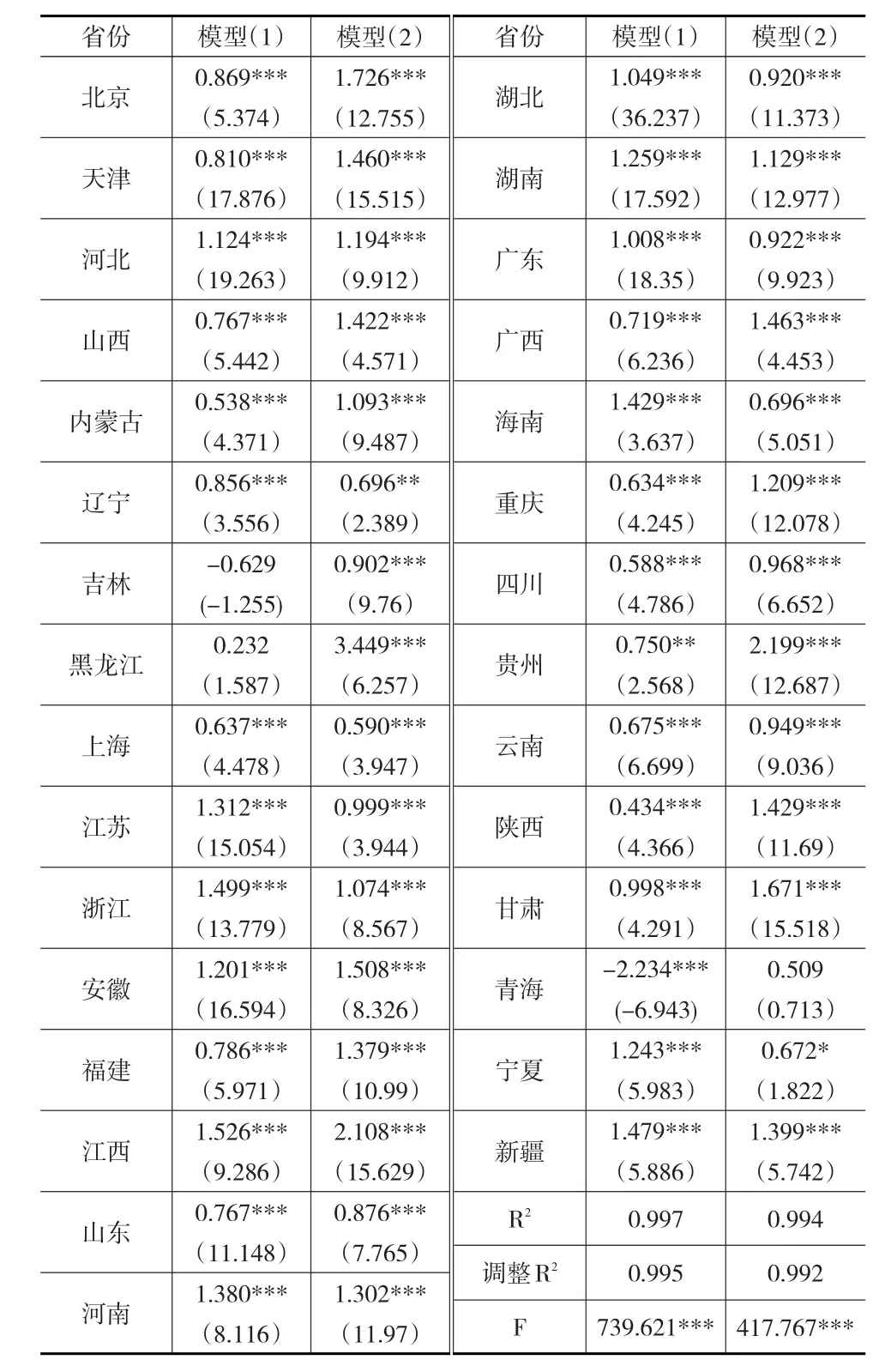
表6 企業R&D投入與產學研協同創新績效模型參數的估計結果

同樣的分析方法可以得到：企業R&D投入對創新科技績效具有積極的促進作用（彈性系數平均水平為1.264）。黑龍江、貴州、江西、北京、甘肅、安徽、廣西、天津、陜西、山西、新疆、福建和河南這13個省份的企業R&D投入對產學研協同創新科技績效的促進作用強于全國其他地區，彈性系數都在全國平均水平以上。企業R&D投入對產學研協同創新科技績效有較差的促進作用的省份有：海南、遼寧、寧夏、上海、青海，彈性系數都在0.8以下。其他省份的企業R&D投入對產學研協同創新科技績效的影響均在全國位于中等水平。

3 結束語

本文使用我國30個省份2009—2015年的有關面板數據分析企業R&D投入與產學研協同創新效果的關系，得到如下結論：（1）我國30個省份企業R&D投入對創新科技績效和創新經濟績效均具有積極顯著的促進作用。所以企業在進行相關創新活動時要積極分析R&D投入與創新績效的正面促進關系，在加強企業和高校、科研機構的協作的同時，也要大規模增加企業R&D人員投入和經費投入，實現R&D資源的優化配置，提高人力、經費的合理、有效使用。（2）企業R&D投入對創新科技績效的促進作用高于對創新經濟績效的促進作用。所以，企業在保證科技績效提升的情況下，要進一步提升經濟績效，提高科技創新成果的轉化率。避免創新目標不明確，創新成果與市場脫節的現象，使創新成果市場化、商業化。（3）對創新科技績效和創新經濟績效的影響都很高的省份有江西、新疆、河南、安徽，很低的省份僅有青海，其他省份則是表現出企業R&D投入彈性系數此高彼低的特點。因此，對創新績效影響低的省份可以采取激勵措施，引進與培養創新型、應用型人才；另外，政府可以加強對這些省份的科研經費投入。