基于邊際效用模型的最佳人力資源管理模型
孫文亮
(南開大學 經濟學院,天津 300071)
0 引言
人力資源在企業資源中占據重要地位,企業只有具備完善的激勵體制,才能儲備更多各行業的優秀人才,進而最大程度地提高員工的積極主動性和創造力,提高企業的經濟效益。目前我國各大小企業中均有相應的激勵機制,但效果并不明顯,這主要是因為缺乏對效用理論的應用。公司的激勵制度按照效用理論可分為物質激勵(邊際效用遞減規律)與精神激勵(邊際效用遞增規律)兩種。在一定時間內,邊際激勵效用會隨著激勵數量的增加而呈遞減趨勢,在原有條件不變的情況下,員工接受到的總效用會隨著激勵的增加而增加,但是效用卻會減少。同時,企業在運用邊際效用模型時,投資成本會一直增加,最終所得報酬增加也會在達到極限后降低。本文運用邊際效用模型構建企業人力資源的優化模型,利用企業經濟增長模型計算出邊際效用的變化,分析人力資源管理對企業生產總值的影響,并對其進行優化配置。
1 邊際效用模型的構建
1.1 邊際效用函數
假設m是人力資源管理質量的指標個數,yj則為第j個指標的資源投入總量,是指標效用。而在市場環境中,人力資源是作為特殊商品存在的,且同樣適用于邊際效用規律——yj與滿足這個規律,即:

顯而易見,與yj之間為上凸曲線,其原點為左端點。將指數分布的概率密度函數作為指標的邊際效用函數,將分布函數作為效用函數,即為:
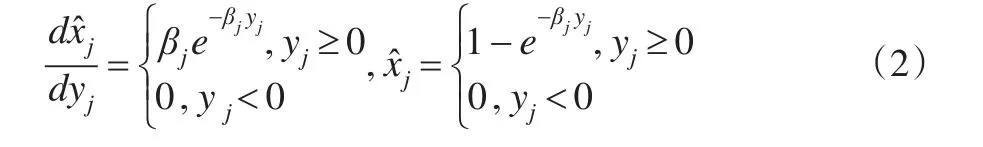
由于/dyj=βj(yj=0),所以,第j個指標所能做到的最大邊際效用為βj。
1.2 基于邊際效用的人力資源管理模型
設人力資源管理總效用為S,資源投入總量為yj,因此:

式(3)中,ωj代表各指標重要性的權重系數,指第j項指標的效用,yj指資源投入總量。接下來構建兩種優化模型。
模型Ⅰ:

模型Ⅱ:
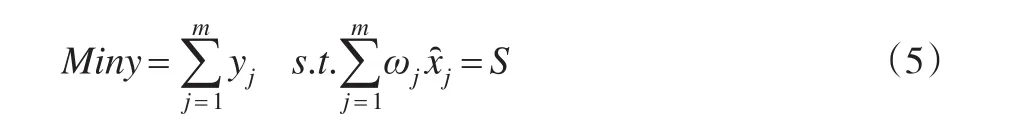
模型Ⅰ的前提條件是在資源投入總量有限的情況下,使其總效用運用最大化的最優化模型;模型Ⅱ是以目標明確為基礎,使投入量最小的最優化模型。
假設在研究過程中,已經精準評估了與yj,可將式(2)變為:

式(6)便是βj的求解式。
1.3 模型求解
(1)模型Ⅰ:
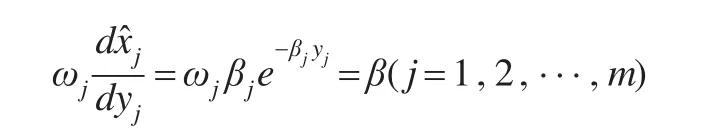
即為:
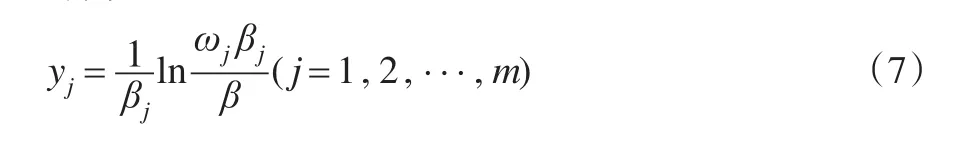
而事實證明,當yj>0時,ωjβj>β,因此只要對其范圍內的指標進行投資,設滿足該條件的指標為前J個指標,則有:
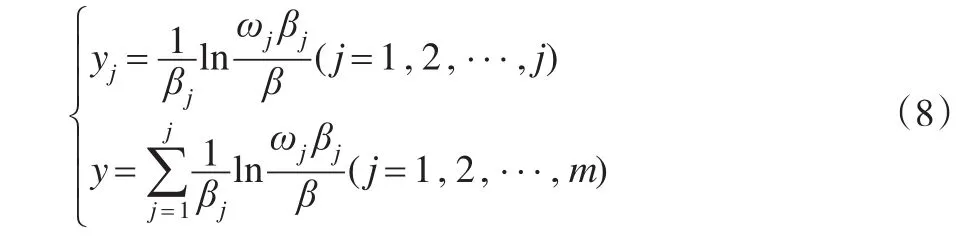

將式(9)中所得的 J值代入式(8),并記?j=可得:
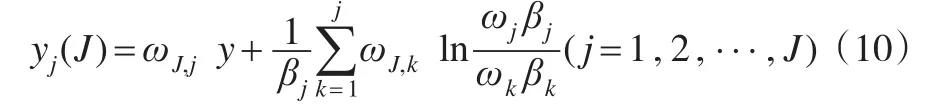
因此,式(10)為模型Ⅰ的最優解。
(2)模型Ⅱ
依據模型Ⅰ:
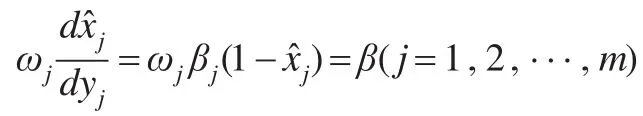
則有:

當>0時,有ωjβj>β,因此只要對其范圍內的指標進行投資,設滿足該條件的指標為前J個指標,則有:
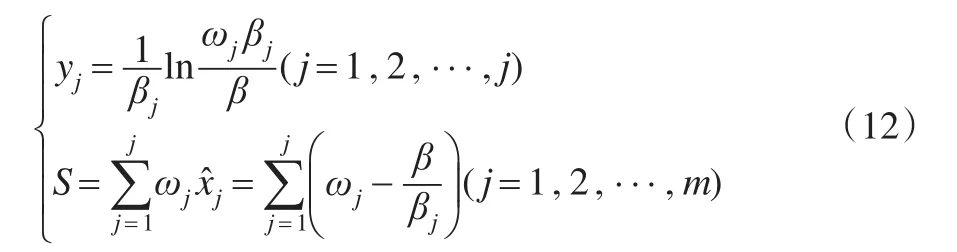
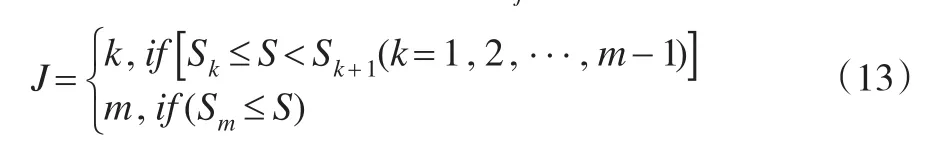
將式(13)的J值代入式(12),可得:
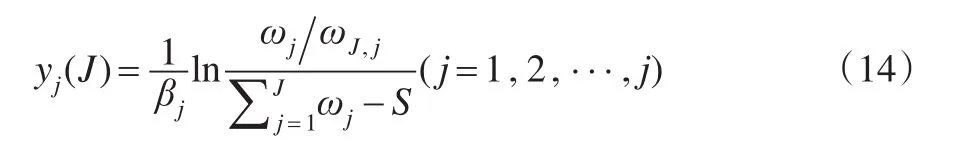
式(14)則為模型Ⅱ的最優解。
1.4 參數求解
現詳細說明并解答上述模型中所含有的參數。
(1)ωJ,j
同時求解式(10):
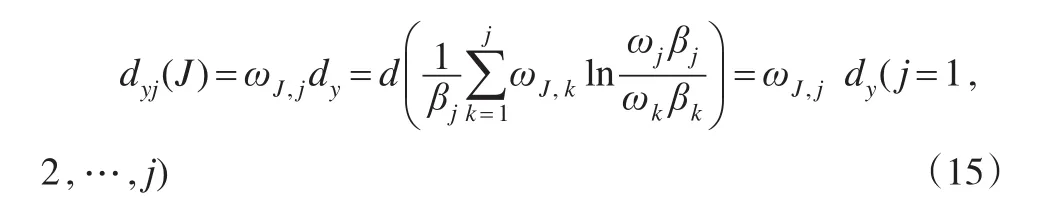
式(15)說明,在模型Ⅰ的最優解中,y每增加dy,各指標相應增加資源同理,求解式(14):
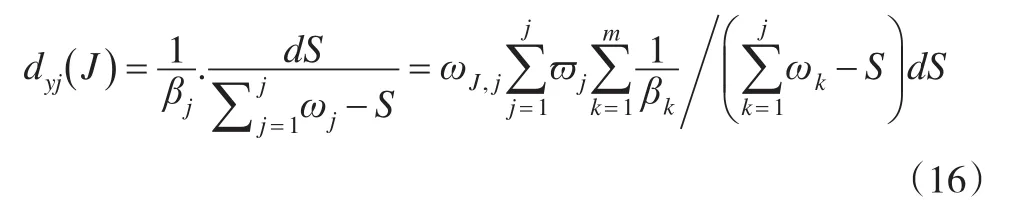
(2)?j
由ωJ,j和?j可知,當J=m時,ωm,j=?j,并可將?j作為指標的特征權重,因此,由式(14)及式(18),查看y→∞和S→1-的極限情況為:
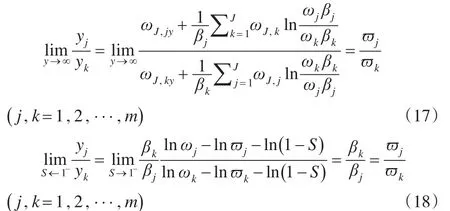
由式(17)和式(18)可知,?j是在y→∞或S→1-的情況下,滿足模型Ⅰ和模型Ⅱ的指標投資權重,?j即是各指標最佳投資權重所得的收斂值。
2 實證分析
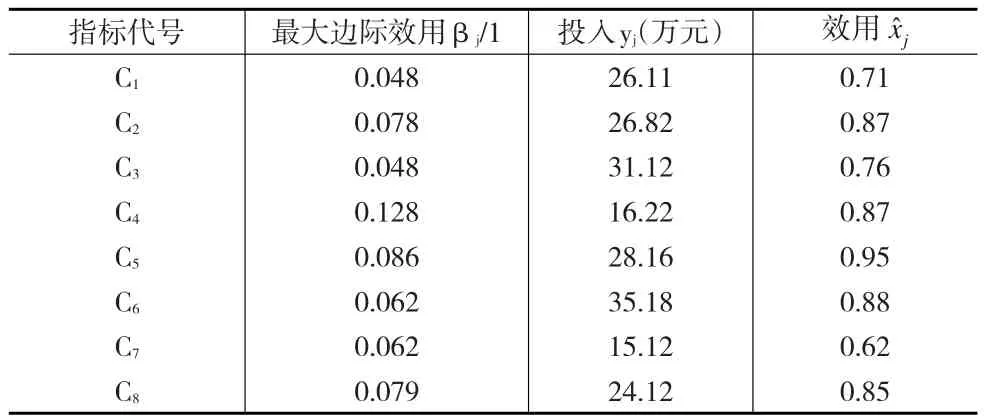
某企業對其專業技術人才管理情況進行績效考核預評價,職位分析與評價、素質模型、人才規劃、職務評任、培養提高等8個一級指標共同組成了評價指標集Cj,其中j的取值為1,2,…,8,ωj、、yj分別代表指標權重、在j指標上產生的效用、各指標資源投入成本(單位:萬元)。表1為某企業人力資源管理質量數據。
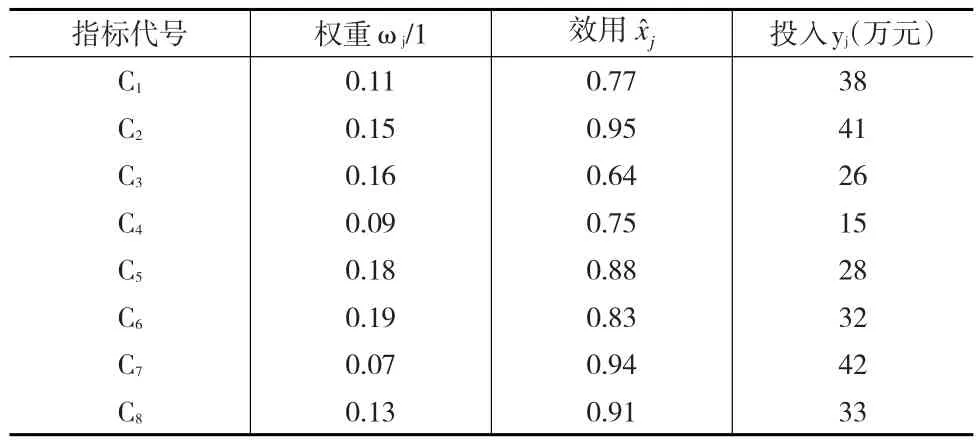
表1 某企業人力資源管理質量評價數據
2.1 基于模型Ⅰ的優化方案
采用模型Ⅰ的優化方案,此方案為管理總效用在固定的272萬元總資源投入下達到最大值。由上述推導結果可以從以下三個步驟求解模型Ⅰ的最優解。
第一步:對最大邊際效用進行計算,根據式(6)對βj進行計算,并按照從大到小的順序對最大邊際效用進行排序;
第二步:對投資范圍J的最佳解進行計算。根據式(9)就能將最佳投資范圍計算出來,y>Y8=103.6,J=12;
第三步:對投資額度的最優值進行求解。當投資范圍為10時,式(10)則為:
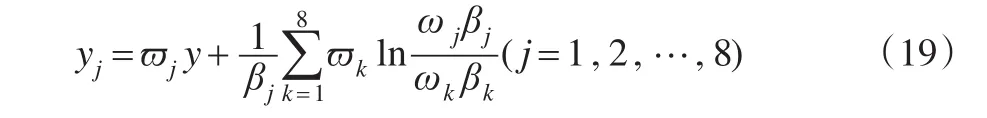
在式(19)中將最大邊際效用值與收斂值?j代入,各指標最佳投資額度yj就能計算出來[1]。
模型Ⅰ的優化方案求解結果如表2所示。

表2 模型Ⅰ的優化方案求解結果
優化方案中,當投入資源計劃總量保持在272萬元的情況下,人力資源管理總效用預期值為0.823,比原方案的總效用提升了4.04%。
2.2 基于模型Ⅱ的優化方案
采用模型Ⅰ的優化方案,此方案為資源投入總量在固定的0.791人力資源管理總效用下達到最小。由上述推導結果可以從以下三個步驟求解模型Ⅰ的最優解。
第一步:對最大邊際效用進行計算,根據式(6)對βj進行計算,并按照從大到小的順序對最大邊際效用進行排序;
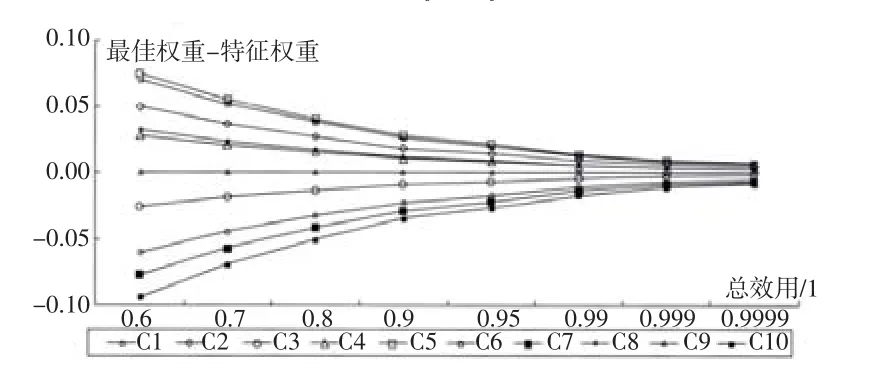
第二步:對投資范圍J的最佳解進行計算。根據式(13)就能將最佳投資范圍計算出來,S8=0.522 第三步:對投資額度的最優值進行求解。當投資范圍為10時,式(14)則為: 在式(20)中將最大邊際效用值與收斂值?j代入,各指標最佳投資額度yj就能計算出來[2]。 模型Ⅱ的優化方案求解結果如表3所示。 優化方案中,當人力資源管理總效用預期為0.791的情況下,計劃人力資源總量的計劃投入僅為251.3萬元,比原方案的資源投入降低了8.24%。 為進一步對指標最佳投資權重與特征權重之間的關系進行分析,本文利用上述算例數據,分析了指標最佳權重隨其他兩個指標的變化趨勢,具體結果如圖1與圖2所示。圖中指標最佳投資權重為[3]: 表3 模型Ⅱ的優化方案求解結果 圖1 指標最佳投資權重隨總效用變化趨勢 圖2 指標最佳投資權重隨資源投入總量變化趨勢 由圖1和圖2可知,模型Ⅰ與模型Ⅱ最佳解的指標權重與相應的特征權重之差隨著不斷增加的總效用與投入總量而逐漸收斂于“0”。因此,各指標最佳投資權重的最終收斂值為指標特征權重。此現象代表:雖然指標最大邊際效用、指標權重與總效用共同影響最佳指標投資權重,但是最佳指標投資權重隨著資源總投入或總效用的增加而受到指標權重與總效用的影響逐漸減小,對其影響逐漸增加為最大邊際效用,并最終向指標特征權重收斂。 本文根據實證結果得出的兩個結論:(1)資源分配結構能夠在其他條件一致的情況下影響組織績效,基于邊際效用的人力資源管理模型能夠通過優化配置管理資源,管理效益最大化得以實現。(2)各指標重要性與指標最大邊際效用共同對最佳資源分配結構產生影響,最大邊際效用的影響會隨著管理效用的增加而增加。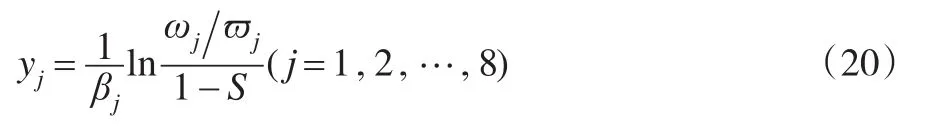
2.3 指標最佳投資權重與特征權重

3 結論

