一種管道卡箍位置自動優化方法

於為剛，趙正大，陳 果，寸文淵，陳雪梅，侯民利

（1.南京航空航天大學 民航學院，南京 210016；2.成都飛機工業（集團）有限責任公司，成都 610092）

管路系統作為現代飛機動力傳輸的主要通道，承擔著輸送燃油、滑油、空氣和液壓油等介質的重要任務，因此在飛機的運行過程中起到極其重要的作用[1]。然而，飛機液壓系統管路的振動問題一直困擾著工程技術人員。隨著現代軍用飛機對作戰性能的要求日益提高，飛機液壓系統逐漸向高壓力發展，工作壓力可以達到21 MPa，甚至28 MPa，管道振動問題也隨之愈加突出。對管道的振動抑制可以采取多種方式，包括管形優化、卡箍優化、以及施加管道減振器等[2]。

安裝卡箍是增加管道系統剛性、減小變形、避免低頻共振的一種主要方式。目前，飛機管道系統中卡箍的布置多是從原型機中對比和移植，再依靠設計者的經驗在實際放樣時做出一定的調整，這樣會造成實際卡箍布局具有較大的隨機性，嚴重影響了管道系統的可靠性，使飛機產生一定的安全隱患[3]。因此，研究復雜管道系統的卡箍位置優化方法具有極其重要的意義。

Wang分別以變形最小化和基頻最大化為目標，采用啟發式優化算法實現了對直梁結構和矩形板結構的支撐位置和優化設計[4-5]；Zhu等采用偽密度技術將離散問題轉化為連續體建立支撐布局的拓撲優化方法[6]；劉偉分別以基頻與外界激振頻率的差值最大化以及隨機振動均方差響應最小化為目標，利用罰函數法對復雜管路的關鍵卡箍位置進行了優化設計[7]。李鑫以激振源固有頻率點的特征阻抗加權和為目標函數，利用粒子群優化算法為飛機液壓管路的優化布局提供了一定的理論依據[8]。

然而，現有研究方法復雜度較高，計算效率很低，難于滿足工程實際的需求。有鑒于此，本文確定以提高管路系統基頻為目標，提出了一種新的基于模態位移的管道卡箍位置自動優化方法，并進行了方法驗證。

1 管道系統模態分析理論

在對管道進行模態分析時，不考慮阻尼和外載荷的影響，管道系統的自由振動方程方程是

其中：M和K分別為管道系統的質量矩陣和剛度矩陣。設自由振動響應為以下形式

代入無阻尼自由振動方程可得

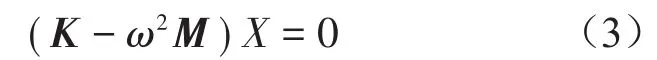
通過求解上述方程可以確定ω和X，其中特征值ω1,ω2,……,ωn代表系統的n個固有頻率，特征向量X1,X2,……,Xn代表對應每一階固有頻率ωi的n個固有振型。

2 卡箍位置的靈敏度分析

安裝卡箍是增加管道系統剛性、減小變形、避免低頻共振的一種主要方式，卡箍位置與剛度對系統振動特性有著重要的影響。為了研究卡箍位置和剛度對管道固有振動特性的影響，針對某一空間管道，獲得管道在施加不同位置和剛度卡箍下的基頻變化，并基于卡箍位置對提高管道基頻的靈敏度分析，得到卡箍位置與剛度對管道基頻的影響規律，進而確定卡箍優化的最佳位置。

建立的空間管道有限元模型如圖1（a）所示，由4根直管和3段彎管構成。導管具體尺寸為：Pipe1=530 mm，Pipe2=930 mm，Pipe3=520 mm，Pipe4=880 mm，外徑為21 mm，壁厚為2.4 mm。導管密度設為7 850 kg/m3，楊氏模量為2×1011N/m2，泊松比為0.3。該導管被離散為22個單元，共計23個節點。

（1）兩端為固定支撐的情形

設S1和S2為管道兩端的固定支撐點，分別布置在節點1和節點23。為了最大程度地提高管道基頻，需要研究卡箍位置對提高管道基頻的靈敏度，得到管道施加卡箍的最優位置。對該支承情形下的管道進行模態分析，管道基頻為12.21 Hz，第1階振型如圖1（b）所示。

圖1 管道模態分析

圖2為第1階振型中各個節點的無量綱振型位移。為了得到卡箍位置對管道基頻的影響規律，選擇在不同位置施加不同剛度的卡箍，表1和圖3都表示了在不同位置和剛度卡箍下的基頻變化情況。從計算結果可以看出：

1）在無量綱振型位移最大的節點施加卡箍能最大程度地提高基頻，是施加單個卡箍的最優位置；

2）當卡箍的剛度在達到某個值時（卡箍剛度在106N/m以上），再增加卡箍剛度對管道基頻無影響，即可以認為是固定支撐。

（2）三點固定支撐的情形

在兩端固定的情形下得到最優卡箍位置為第1階振型位移最大處，在該處（節點12）設置1個固定支撐S3，即設定已經優化好的卡箍，卡箍剛度為108N/m，如圖4（a）所示。對3點固定支撐下的管道進行模態分析，管道的基頻為30.26 Hz，第1階模態振型如圖4（b）所示。為了進一步提高管道基頻，需要繼續增加卡箍，現在需要解決如何以最少的卡箍最大程度地提高管道基頻的問題。

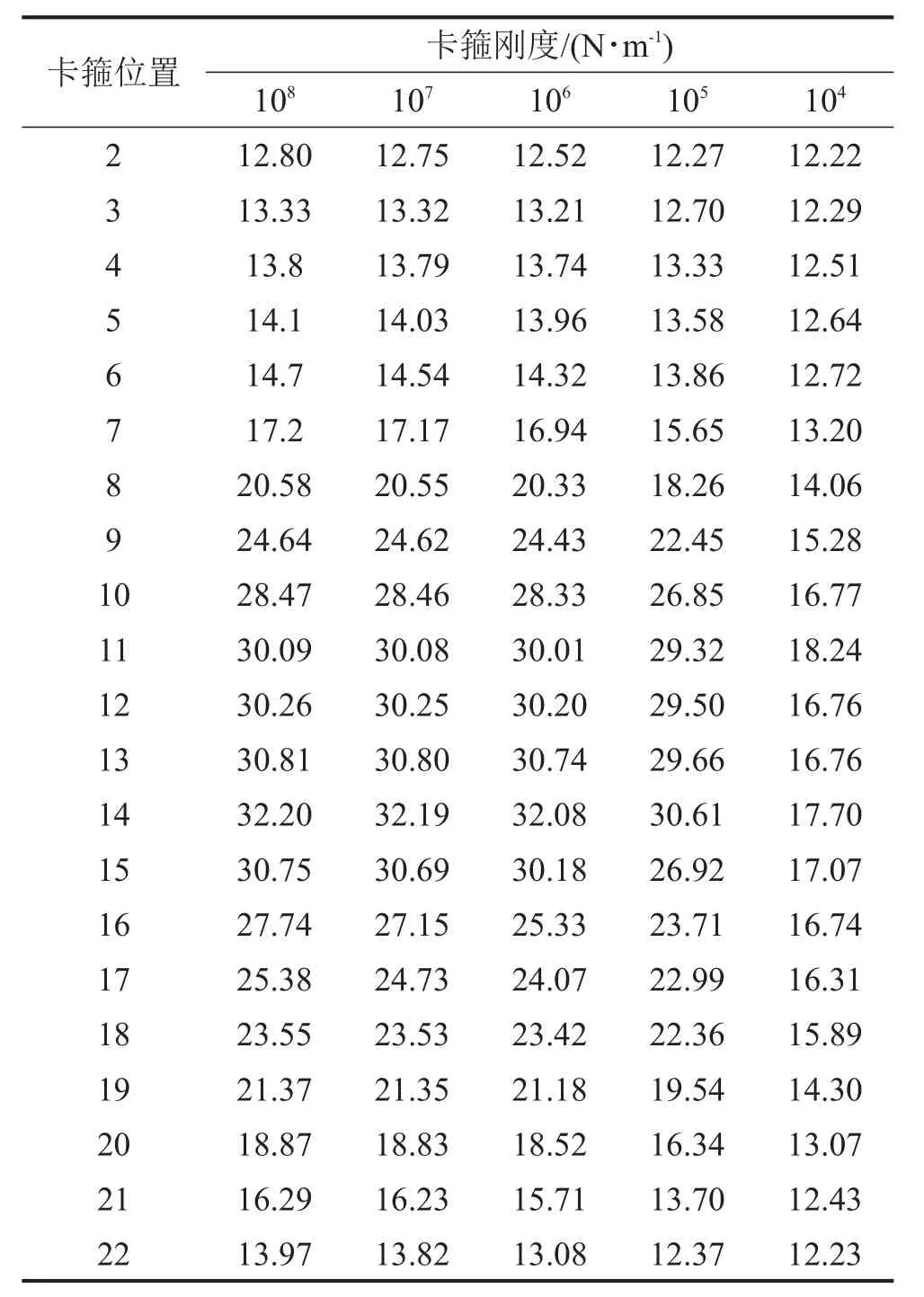
表1 卡箍不同位置和剛度下的管道基頻/Hz

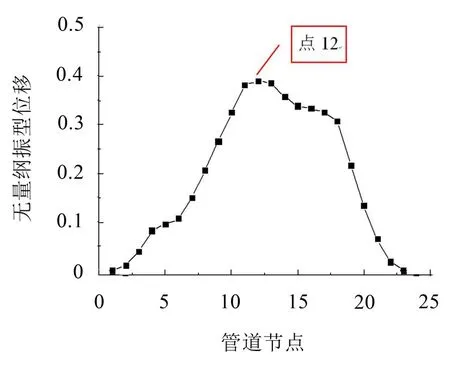
圖2 第1階振型位移

圖5為第1階振型中各個節點的無量綱振型位移，從振型圖中可以看出，在3個固定點間出現了2個極大值點。

根據2點固定下的管道分析結果，可以設想，要想進一步最大程度地提高管道基頻，可以在每2個卡箍固定點間的振型位移極大值點處施加1個卡箍，即在3個固定點下需要同時施加2個卡箍。

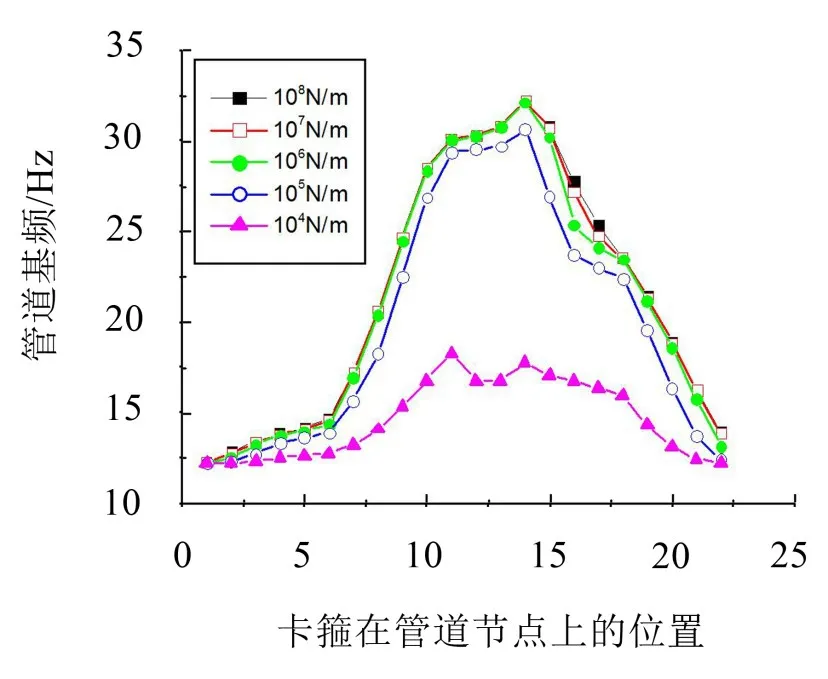
圖3 不同卡箍位置和剛度下的管道基頻

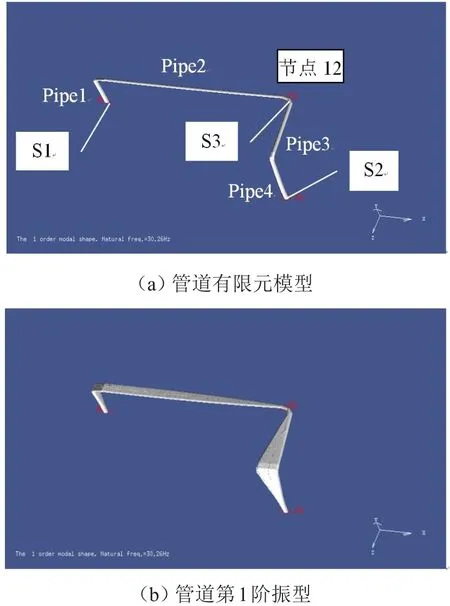
圖4 管道模態分析

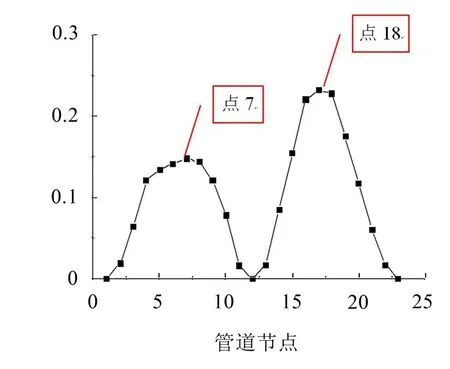
圖5 第1階振型中各個節點的無量綱振型位移

為了驗證這一想法，計算比較了在不同位置同時施加兩個卡箍的管道基頻，其中1個卡箍加到節點2到節點11之間，另一個加到節點13到節點22之間，卡箍剛度設定為108N/m。

表2為不同卡箍位置和剛度下的管道基頻。從計算結果可以看出：3點固定不加卡箍時，基頻為30.26 Hz；3點固定施加2個卡箍時，管道基頻最大提高到110.67 Hz，卡箍位置正好對應于第1階振型位移的2兩個極大值點，分別為節點7和節點18，這與設想中提出的卡箍最優位置完全一致。由此，可以得出結論： 22個固定間點的模態位移極大值點是進一步提高管道基頻的最優卡箍位置點。

3 基于模態分析的卡箍優化方法

根據上述卡箍位置對提高管道基頻的靈敏度分析，得到卡箍位置對管道基頻的影響規律：兩個固定間點的模態位移極大值點是進一步提高管道基頻的最優卡箍位置點。基于此規律提出了1種管道卡箍位置自動優化方法，其基本流程框圖如圖6所示。主要步驟為：

（1）導入給定初始固定支撐位置的初始管道模型；

（2）通過模態分析得到管道系統的基頻及對應的第1階振型；

（3）判斷基頻是否達到目標值，如果達到則輸出卡箍位置、數量及管道基頻；如果沒有達到，則在第1階振型的極大值點處施加卡箍，得到新的管道模型；

（4）轉入步驟2，計算新的管道模型，直至管道系統的基頻滿足要求。

4 卡箍優化方法驗證

為了驗證管道卡箍位置自動優化方法的正確性，選擇了《GJB 3054-1997飛機液壓管路系統設計、安裝要求》中針對特定管型給出卡箍施加的最優位置進行對比。該要求中提到：流速突變會在管路系統中產生沖擊壓力，換向閥快速切換會產生大的沖擊壓力，作動筒活塞快速止動時也會引起液壓沖擊。沖擊壓力在導管中以音速傳播，當壓力傳到導管轉彎處就產生1個側向力，使導管彎曲，并使導管承受彎曲應力，彎曲成U型和Z型的導管受影響較大。一些固定不良的管路系統，當產生液壓沖擊時會發生大的導管位移和振動。如圖7所示。

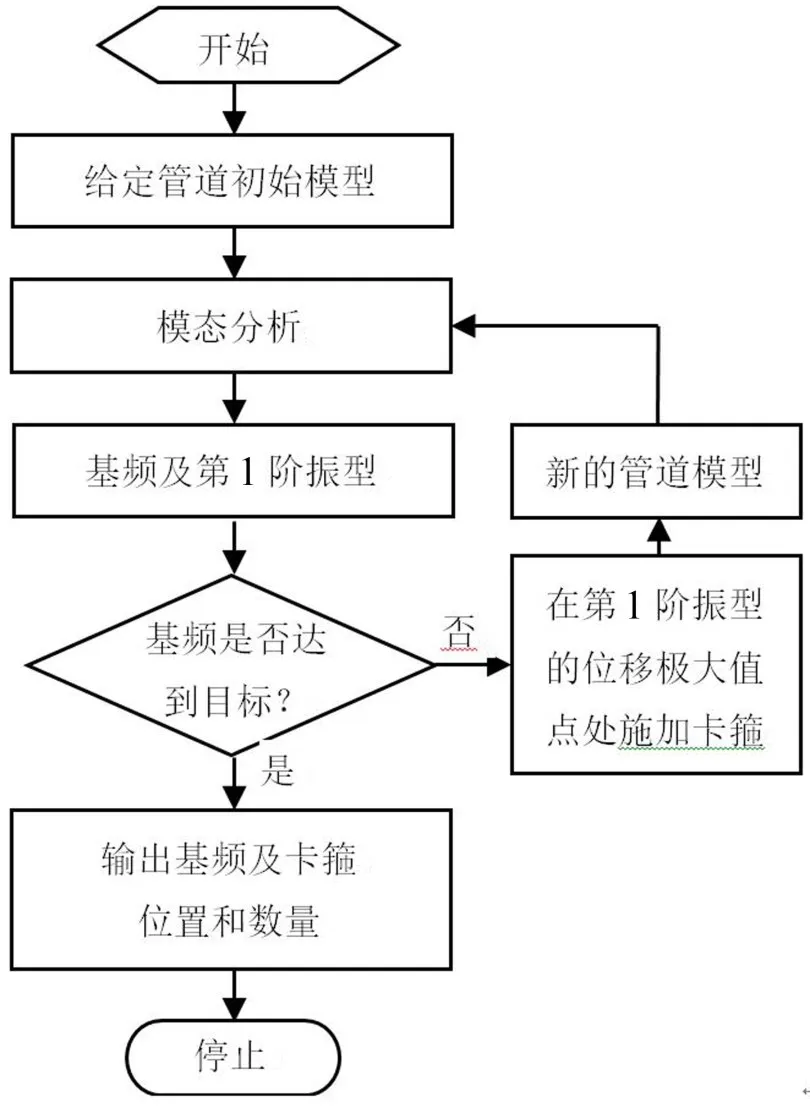
圖6 管道卡箍優化流程

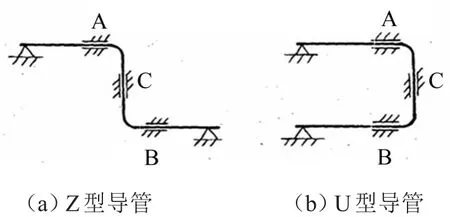
圖7 GJB 3054-1997飛機液壓管路系統設計、安裝要求

僅在C處設置管夾難以阻止導管運動，襯墊易磨損，導管也易受損，應繼續在A或B設置管夾。

4.1 Z型導管分析

根據圖7（a）建立一段Z型管道有限元模型，導管各段長度如圖8（a）所示，L1=0.5 m，L2=0.35 m，L3=0.5 m，導管外徑為20 mm，壁厚為1 mm。導管密度設為7 850 kg/m3，楊氏模量為2.07×1011N/m2，泊松比為0.3。導管兩端設置為固定支撐，將導管離散為42個單元、43個節點。

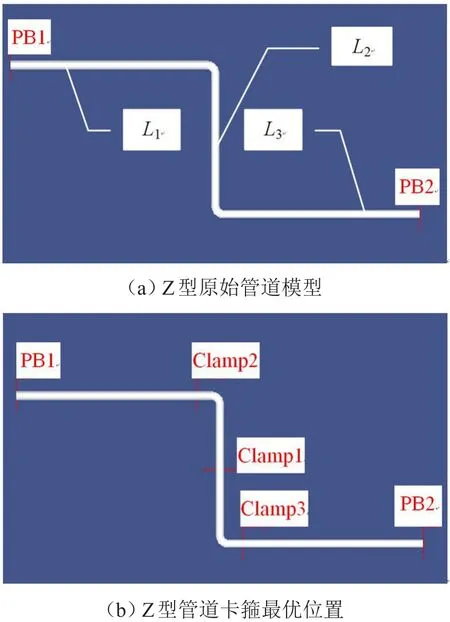
圖8 Z型管道分析與優化

圖8（b）和表3為優化結果，從表3可以看出，在不加卡箍時，管道基頻為47.79 Hz，第一次優化結果為在節點22處施加一個卡箍，基頻提高到149.78 Hz；第二次優化結果為在節點13和31再各增一個卡箍，基頻提高到354.11 Hz。與圖7（a）對比發現，卡箍優化結果與GJB 3054-1997中提到的Z型管道卡箍設置結論相同，驗證了卡箍優化方法的正確性與有效性。

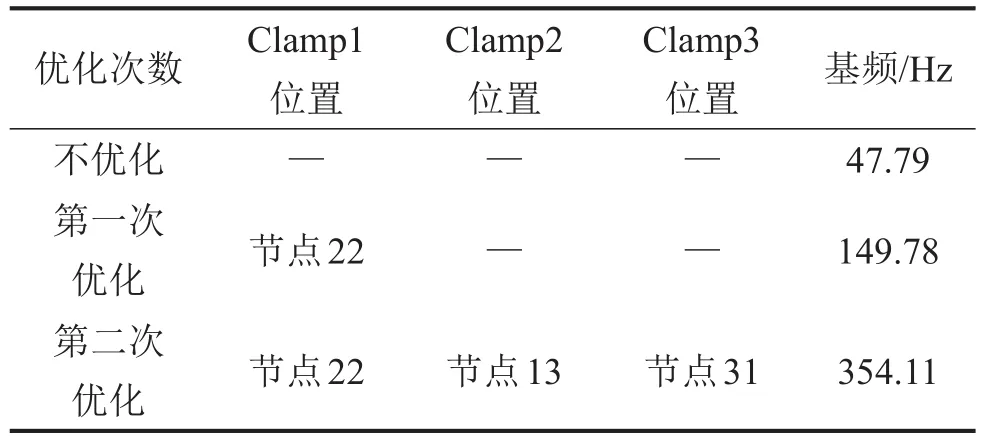
表3 Z字形管道卡箍優化結果

4.2 U型導管分析

根據圖7（b）建立一段U型管道有限元模型，導管各段長度如圖9(a)所示，L1=0.5 m，L2=0.35 m，L3=0.5 m，導管外徑為20 mm，壁厚為1 mm。導管密度設為7 850 kg/m3，楊氏模量為2.07×1011N/m2，泊松比為0.3。導管兩端設置為固定支撐，將管道離散為42個單元、43個節點。

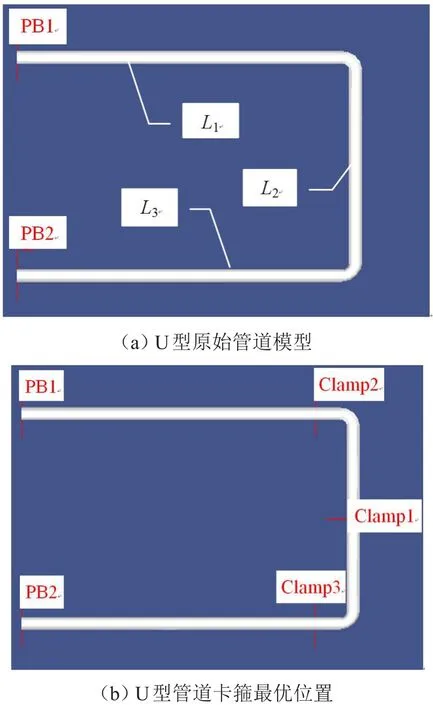
圖9 U型管道分析與優化

圖9（b）和表4為優化結果，從表4可以看出，在不加卡箍時，管道基頻為33.83 Hz，第一次優化結果為在節點22處施加1個卡箍，基頻提高到149.79 Hz；第二次優化結果為在節點13和31再各增一個卡箍，基頻提高到354.72 Hz。與圖7（b）對比發現，卡箍優化結果與GJB 3054-1997中對U字形管道的卡箍設置結論相同，驗證了卡箍優化結果的正確性與有效性。

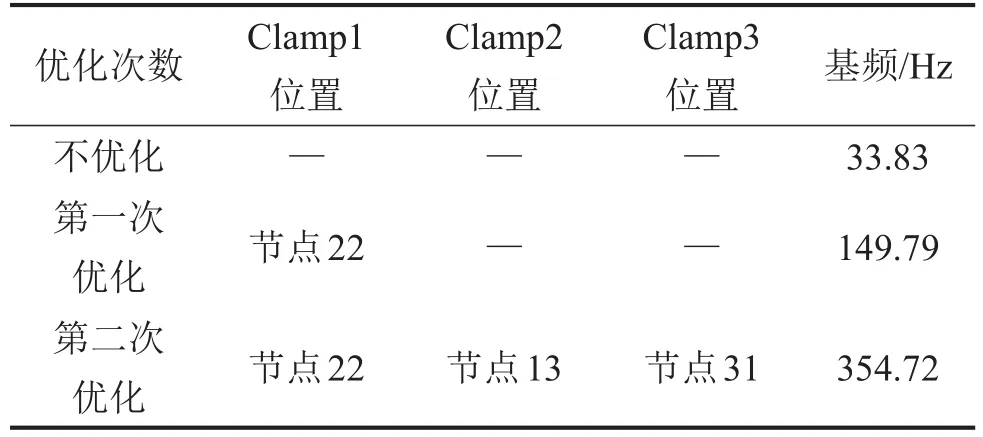
表4 U字形管道卡箍優化結果

5 結語

（1）基于卡箍位置對管道基頻的靈敏度分析研究了卡箍對基頻的影響規律，以提高管道基頻為目標，提出了一種基于管路系統模態位移的卡箍位置自動優化的方法。

（2）利用GJB相關規范中的Z形和U形管道進行了方法驗證，結果充分表明了新方法的簡便性和有效性。