高速鐵路扣件彈條性能分析及頻響特性研究

施何瑛，王安斌，高曉剛

(上海工程技術大學 城市軌道交通學院，上海 201620)

高速鐵路無砟軌道扣件系統是軌道結構重要組成的一部分，彈條作為扣件系統的關鍵部分，起固定鋼軌、保持軌距、吸收來自鋼軌的沖擊等作用，扣件系統的穩定性直接影響高速列車運行的安全性和舒適性[1]。彈條一旦發生失效，輪軌之間相互作用力會極具加劇，縮短扣件的使用壽命，嚴重時會引起列車脫軌。因此，開展彈條性能參數及頻響研究，分析各動靜參數之間的關聯影響，對扣件系統設計的具有一定理論指導意義。

對于扣件系統，大量國內外學者從不同角度對其進行研究與分析。文獻[1]采用FMECA分析法和故障樹分析法對W300型扣件系統進行結構分析，找出扣件易損部分，并結合現場故障對整個扣件系統可靠性進行評估。文獻[2]運用有限元軟件分析WJ-7型彈條在不同沖擊力作用下彈條最大應力發生的位置以及最大應力值，結果表明彈條在與鐵墊板接觸區產生最大應力，應力值為1 853 MPa。文獻[3]從時頻域角度研究分析e型彈條斷裂的根本原因，結合現場測試結果，揭示彈條斷裂的主要外因是彈條自然狀態下和服役狀態下的前兩階頻率與現場波磨通過頻率發生共振。文獻[4]從動力學角度，研究扣件在高速列車動荷載作用下的振動特性，以Vossloh彈條為研究對象，基于非線性接觸理論，得到彈條在安裝狀態下及列車動荷載作用下的振動特性，并于現場實測結果對比驗證。揭示了彈條在螺栓預緊力為33 kN時達到正常安裝狀態，此時彈條中環位移為20.3 mm，扣壓力為13.8 kN。文獻[5]建立扣件系統有限元模型，研究扣件系統軌下膠墊的位移以及應力。文獻[6]基于非線性動力學理論，分析扣件系統橡膠隔振器的振動特性。

綜上可見，國內外學者對扣件系統的研究很多，但是很多研究只是基于獨立的彈條或者扣件系統的其他部分而非針對彈條研究，并且缺少理論研究之后的實測驗證。基于此，本文以某型高鐵扣件SKL-15型彈條為例，采用ABAQUS有限元軟件建立詳細的扣件結構，基于模態理論和現場彈條頻響分析，得到彈條在安裝過程中的性能參數關系及振動頻響特性。

1 扣件彈條建模

彈條由于線形復雜、參數多且相互關聯，成為扣件系統設計的難點。為了能準確模擬扣件在安裝狀態下的性能，本文扣件系統各個零件均按照標準尺寸建模。其中彈條模型通過“中心線掃描法”建立模型，中心線主要通過Solidworks中的二次“投影曲線”和二次“組合曲線”操作完成，在建模時要注意彈條每個視圖所對應的曲線，并且找準點與點、線與線之間的幾何關系。彈條模型如下圖1。

圖1 某型扣件SKL15彈條模型

2 彈條模態理論和頻響理論

2.1 模態分析理論

結構的振動特性決定自身以及與其關聯系統的動態響應特性，模態分析[7]的主要作用就是確定結構和機械零部件的振動特性。根據彈性力學理論知識，建立扣件系統無阻尼運動方程為

把由機械系統的n個主陣型（即主模態）按階次排序成一個n階方陣（或振型矩陣）。

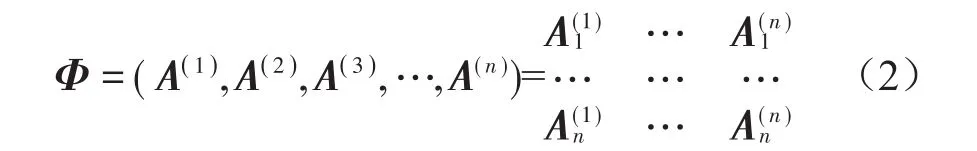
以模態矩陣對該方程作線性變換

變換后得到模態方程為

式中：M為模態質量矩陣，K為模態剛度矩陣。

對應的特征方程為

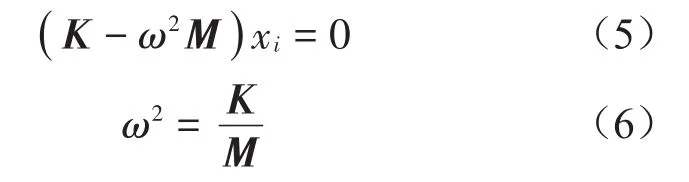
式中：ω2為彈條系統第i階的模態固有頻率，且i=1，2，3，…，n坐標變換矩陣Φ對應的每一列即模態振型。

2.2 頻響理論

頻率響應法是利用控制系統的正弦輸入信號與相應輸出信號之間的關系來分析系統性能的方法。頻響函數是響應和力經過傅里葉變換之后的比值。且頻響函數對結構的動力特性測試具有特殊重要的意義。假設在一個線性系統中，激勵為X(t)，響應為Y(t)，對激勵和響應這兩個時域信號進行傅里葉變換得到它們的頻譜X(ω)，Y(ω)，則可得到頻響函數

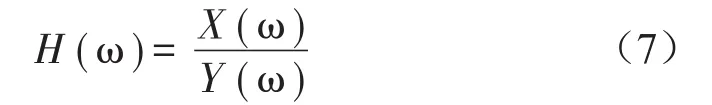
式中：X(ω)為激勵頻譜；Y(ω)為響應頻譜。

3 某型扣件SKL15彈條仿真分析

3.1 有限元模型約束設置

為了使得模擬結果更接近真實情況，模型采用非線性接觸[9-10]理論來處理扣件系統的邊界條件。模型中將鋼軌考慮為解析剛體，其他彈條接觸區均根據真實幾何尺寸裝配，定義彼此間合適的接觸關系。其中，法向接觸采用ABAQUS軟件中的“Hard”，即兩物體間不允許相互貫穿或者侵入，接觸面減的法向接觸只能是壓力[11]；切向接觸采用庫倫摩擦模型，并且引入一個允許“彈性滑動“的罰摩擦公式來處理粘結和滑移兩種狀態間的不連續性可能導致不收斂問題[12]。

3.2 材料參數

軌下剛度為26 kN/mm，接觸面間的摩擦系數為0.3。

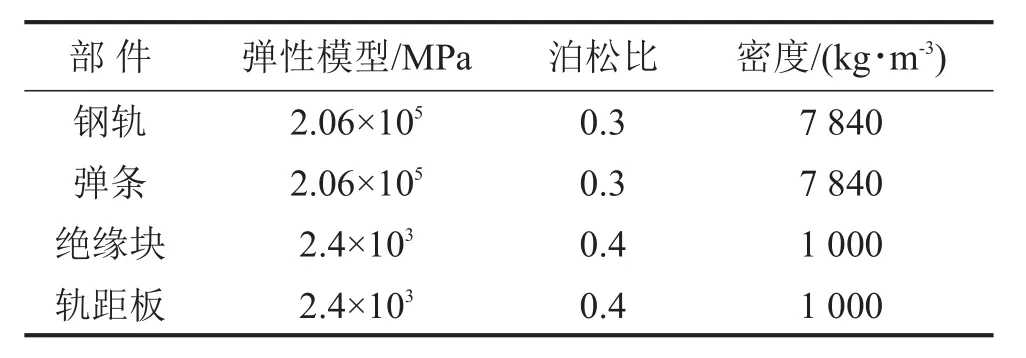
表1 材料參數

3.3 自由狀態模態分析

為了解彈條自由狀態下的固有振型，模型中未對彈條設置任何接觸或者約束，考慮彈條在2 000 Hz以內的固有頻率[13]，其前4階振型圖如圖2(a)－圖2(d)所示。

圖中實線部分代表原始狀態，陰影部分為變化振型，從振型圖中可看出在頻率為440 Hz時，彈條側肢出現翻轉振型，且最大應變出現在彈條跟部，這與現場彈條出現問題的位置一致，由此推測彈條在該頻率下長期運動會導致彈條疲勞失效。詳細振型描述如下表2。

圖2 前4階振型圖

3.4 組裝狀態下模態分析

為研究彈條在服役狀態下的頻率以及振型特點，對彈條進行組裝模態分析，考慮到高鐵現場輪軌激勵關注頻段，組裝模態同樣考慮2 000 Hz以內的頻率，有限元模型如圖3所示，詳細振型描述如表3所示。

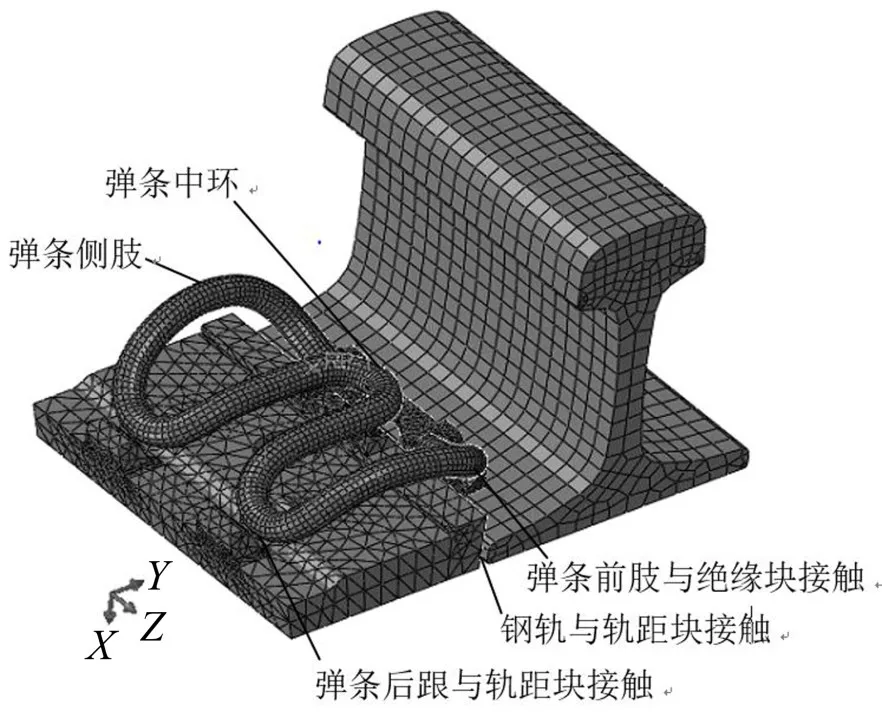
圖3 組裝扣件有限元模型

表2 彈條自由狀態下固有頻率及振型

表3 彈條服役態下固有頻率以及振型

3.5 不同扭矩下彈條性能參數分析

為了分析不同安裝扭矩下組裝彈條參數的性能。按照標準要求安裝扣件系統，通過調節不同的螺栓扭矩，得到彈條在正常組裝狀態下的中環位移、螺栓預緊力以及扣壓力，結果如表4及圖4。按照供貨條件，此型扣件扭矩一般為250 N?m，當扣壓力達到9 kN時，彈程為13.4 mm。

4 軌道結構頻響分析

為進一步了解彈條頻響特性，分析彈條在正常安裝狀態下的敏感頻率，在某高鐵試驗段進行了軌道結構頻響測試，如圖5。

由圖6可知，彈條彈跟和彈拱的峰值頻率184 Hz為扣件支承剛度主導的彈條垂向固有頻率；彈條峰值頻率620 Hz與組裝模態所得632 Hz基本吻合，可能為組裝扣件系統彈條共振頻率，最后導致扣件疲勞失效。

表4 組裝狀態下扣件性能參數表

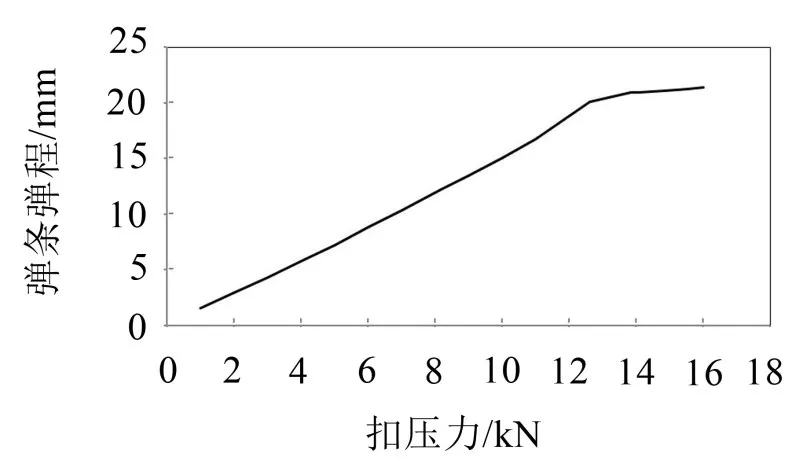
圖4 扣壓力結果圖

圖5 軌道結構頻響測試圖

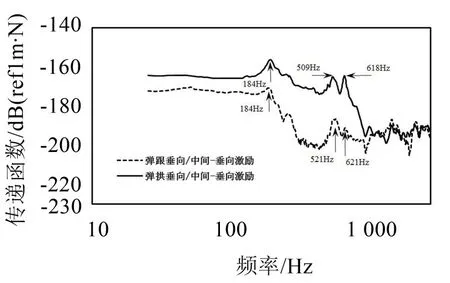
圖6 頻響分析圖

5 結語

(1)綜合考慮彈條在自由狀態以及正常組裝狀態下的振動特性，得到彈條同振型的模態頻率，分別是297 Hz、440 Hz、758 Hz、1 292 Hz和363 Hz、632 Hz、1 233 Hz、1 645 Hz。

(2)通過室內扭矩試驗，得到彈條在正常組裝條件下不同扭矩與扣壓力和彈程的關系，按照此型扣件供貨條件，當扭矩為250 N?m時，扣壓力為9 kN，此時彈程為13.4 mm。

(3)根據某高鐵試驗段的軌道結構頻響測試，得到彈條頻響分析結果，彈條峰值頻率約620 Hz與模態頻率632 Hz基本吻合，可能引起扣件系統共振，導致彈條疲勞失效。