斜交45°現澆箱梁設計計算研究
萬夢
招商局重慶交通科研設計院有限公司 重慶 400067
1 引言
由于項目路線跨越河道或者結構物,為減小對結構物的干擾或讓橋梁順適河道水流的流向,減小橋墩對河道的干擾同時能滿足通航需求等原因,在選取橋梁方案時采用斜交布跨的方式較多。特別在高速公路、一級公路等建設條件下,在采用斜交的情況下不僅能減小對結構物和河道等因素的干擾,讓路線平面更加的舒適,還可以減小橋梁長度、節省造價,所以斜交橋梁在上訴工程中應用廣泛。在采用斜交梁橋時其受力特性和正交梁橋在受力上有著較大的差異,由于支座是斜向布置導致了其扭剪效應特別的突出。同時多跨的斜交連續梁結構受力比簡支結構更為復雜,在計算時對應力,扭矩等控制更為的嚴謹。
坳頭大橋為了適應路線變寬故采用四跨預應力連續斜橋箱梁。坳頭大橋為整體式橋梁,橋跨布置為8×30m,共2聯,本橋平、立面均處在曲線上,且橋跨處在變寬段,為了順應瀏源河的水流方向和滿足行洪要求,橋跨斜45°布置。本橋上構采用預應力砼現澆箱梁橋,下構橋墩為樁柱式橋墩,橋臺為重力式U型橋臺和擴大基礎。
2 斜橋受力特點
斜橋的主要受力特點:
(1)在橋梁的鈍角位置的支座反力要大于其銳角位置的支座反力,同時銳角位置可能會出現支座脫空現象;斜交的角度越大,鈍角處的支座反力和銳角處的支座反力相差越大。
(2)斜交時支座采用的是斜向布置,支座位置有很大的扭矩。
(3)斜交橋梁在彎扭耦合作用下,跨中彎矩要比正交橋梁要小,斜角角度進一步加大,其跨中彎矩折減越大;不過在彎扭作用下其跨中扭矩越越來越大。
(4)在活載、制動力、溫度梯度、預應力效應等作用下,由于平面各個方向的位移不一致,使得平面出現彎矩,該作用讓橋梁出現鈍角方向朝銳角方向轉動的趨勢;如果出現了使橋梁伸縮出現限制的因素出現,如梁端伸縮縫縫隙被堵住和預留空間不足等這類的情況出現,箱梁轉動的形勢更大。
對于梁格法的橫向剛度,Midas幫助文件中有如下描述:“對斜交橋梁多用梁格法進行建模。 可用斜交梁格或正交梁格來建模。對于斜交角度小于20時,使用斜交梁格是非常方便的。但是對于大角度的斜交橋,根據它的荷載傳遞特性,建議選用正交梁格,而且配筋時盡量沿正交方向配筋。”
坳頭大橋的構件形式采用現澆預應力混凝土連續箱梁橋,跨徑為2x(4x30)m,斜交角度45度,汽車荷載采用公路Ⅰ級,箱梁選用C50混凝土,箱梁頂板厚度為25~50cm,底板厚度為22~37cm,腹板厚度為50~80cm,腹板變化段長度為5m,橋面寬度為21.13~30.17m,箱室為三室變四室。橋梁橫截面布置圖如圖1。

圖一 箱梁跨中橫截面布置圖
3 結構建模分析
本橋采用Midas Civil建模分析,由于考慮到斜橋效應本文建立兩種模型進行對比,分別為正交梁格模型和單梁模型,Midas模型如圖二至圖四所示

圖二Midas梁格模型
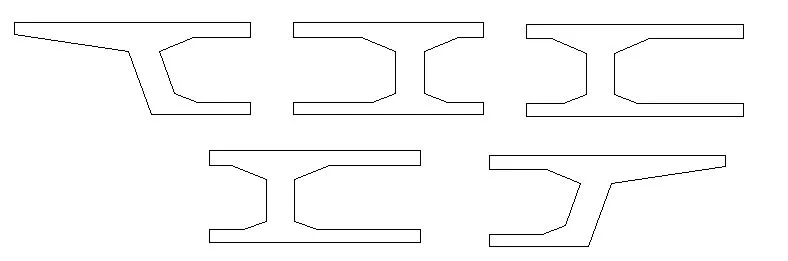
圖三 劃分的梁格斷面
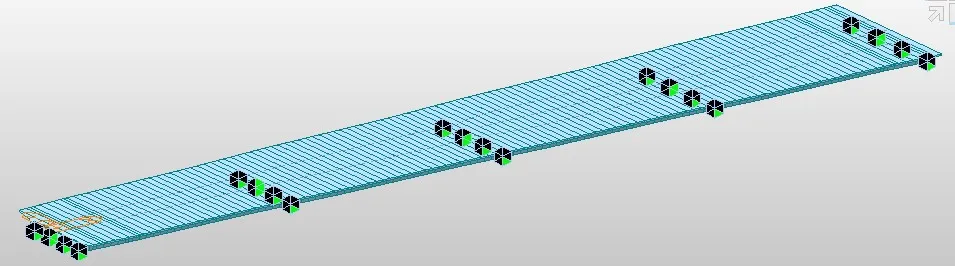
圖四 Midas單梁模型
Midas梁格模型中把箱梁劃分為五個縱梁,在實際的橫隔板處用橫梁模擬,橫向連接梁間用虛擬橫梁模擬,定義梁截面時選擇梁上緣對齊方式,支座點的建立,可由梁上緣對應節點向下復制支座節點,并用剛性進行梁與支座的連接,支座沿橋軸線法向方向斜45度布置。Midas單梁模型中支座點的建立采用正交布置。
4 梁格模型與單梁模型計算分析
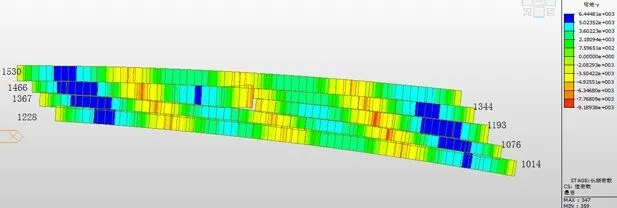
圖五 梁格模型彎矩M-y圖
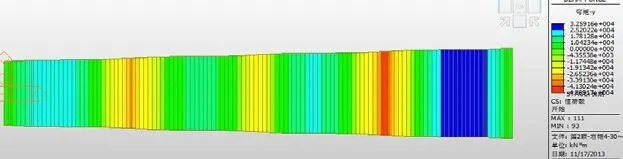
圖六 單梁模型彎矩M-y圖
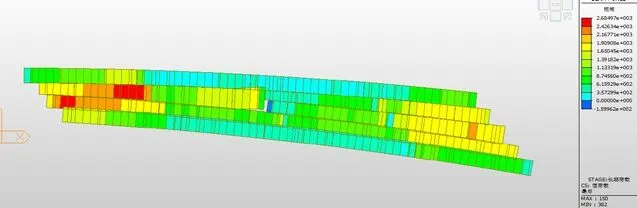
圖七 梁格模型扭矩圖
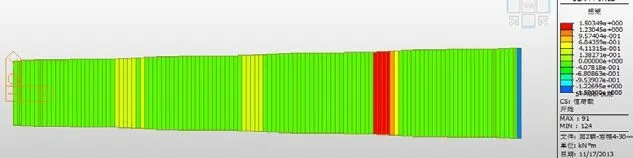
圖八 單梁模型扭矩圖
經計算梁格模型彎矩M-y在第一跨支點為-2628.8KN*m,第一跨跨中為6352.5KN*m;第二跨支點為-8288.5KN*m,第二跨跨中為5057.3 KN*m;第三跨支點為-6318.2 KN*m,第三跨跨中為4244.6KN*m;第四跨支點為-9189.4KN*m,第四跨跨中為6444.8KN*m。單梁模型彎矩M-y在第一跨支點為-4205.5KN*m,第一跨跨中為23108.9KN*m;第二跨支點為-37033.7KN*m,第二跨跨中為13137.4KN*m;第三跨支點為-21781.3KN*m,第三跨跨中為18442.1KN*m;第四跨支點為-48691.7KN*m,第四跨跨中為31949.2KN*m。
經計算梁格模型扭矩在第一跨支點為1563.4KN*m,第一跨跨中為2684.3KN*m;第二跨支點為951.0KN*m,第二跨跨中為1262.0KN*m;第三跨支點為1320.0KN*m,第三跨跨中為923.0KN*m;第四跨支點為1054.7KN*m,第四跨跨中為2168.3KN*m。單梁模型扭矩計算結果幾乎為0。
由上述可以看出,用單梁模型的跨中和支點的彎矩M-y遠大于梁格模型的彎矩M-y,但是單梁模型中扭矩幾乎處處為零,這樣子不符合斜橋的彎扭耦合作用計算依據。所以在計算斜橋時應采用正交梁格模型。
根據梁格模型結算結果0號支點左側墩頂反力為634.6kN,右側墩頂反力為1367.3 kN;1號支點左側墩頂反力為1249.7 kN,右側墩頂反力為2855.3 kN;2號支點左側墩頂反力為1445.8kN,右側墩頂反力為1682.0kN;3號支點左側墩頂反力為1079.2 kN,右側墩頂反力為2855.3kN;4號支點左側墩頂反力為2739.5 kN,右側墩頂反力為1374.1kN。
斜交箱梁在自重作用下的支座反力不相同,銳角處出現較小反力,當斜交角度越大時,銳角處有可能出現支座脫空現象,斜交箱梁最大彎矩向鈍角方向靠攏,同時在自重作用下,斜交箱梁存在較大的扭矩,具有明顯的空間受力特性,這些效應的大小與斜交角度大小也有很大的關系,斜交角度越大,上述效應就越大,一般來說斜交角度小于20時,對于斜交橋的上述影響可以忽略,如果斜交角度超過20度,就必須考慮上述效應的影響。
5 預應力效應
預應力效應見圖九。
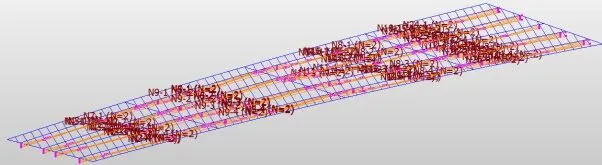
圖九 梁格法預應力束形
計預應力與不計預應力時墩的反力取用該橋兩端的支座反力,其具體數據如下所示。
計預應力時左側墩頂的反力總和為6214.2KN,右側墩頂的反力總和為8296.6KN;不計預應力時左側墩頂的反力總和為6270.1KN,右側墩頂的反力總和為8307.6KN。計預應力時1號支點左側墩頂反力為949.7KN, 右側為2855.3KN;不計預應力時1號支點左側墩頂反力為538.5KN, 右側為4292.7KN。
由此可以得出:(1)由預應力效應引起的反力在合計的情況下幾乎與未計預應力效應下一樣,但是在各個支座上的有著區別。(2)預應力效應使得各個支座的反力更加的均勻。(3)預應力效應對于斜交在各個支座上橋梁鈍角大和銳角處小的現象沒有影響。
6 結論
梁格法是橋梁結構空間分析的一種有效方法,由于其具有基本概念清晰,易于理解和使用的特點,在進行斜橋分析時往往采用該方法。斜交梁橋在彎扭耦合作用下其扭矩,剪力等要比正交梁橋大,空間受力特性更加明顯,故對于斜角角度大于15度的梁橋不宜采用單梁法來建模計算,而應該采用更為合理的梁格法來進行分析。
根據前幾節的結論,斜交梁橋其自身的受力特性,在耐久性和經濟性等因素上有所欠缺。不過在設計上可以通過采用梁格法進行計算后對于跨徑較大的橋梁增加跨中橫隔板,在橫梁處加大橫向鋼筋的配置,增設鈍角和銳角角域鋼筋等措施來緩解上述因素。

