地形起伏地區平面坐標轉換方法及精度分析
馬海英,胡月明,姚朝龍,范亞南,,胡碧霞,張 偉
(1. 德令哈市國土資源局,青海 德令哈 817000; 2. 華南農業大學資源環境學院,廣東 廣州 510642;3. 國土資源部建設用地再開發重點實驗室,廣東 廣州 510642; 4. 廣東省土地利用與整治重點實驗室,廣東 廣州 510642; 5. 廣東省土地信息工程技術研究中心,廣東 廣州 510642; 6. 青海大學農牧學院,青海 西寧 810016; 7. 廣州市華南自然資源科學技術研究院,廣東 廣州 510642; 8. 青海友元空間信息技術有限公司,青海 西寧 810008)
隨著測繪理論和技術的發展,我國在不同時期建立了不同的坐標系,包括1954北京坐標系、1980西安坐標系、2000國家大地坐標系。為了統一使用不同坐標系下的成果,通常需要進行坐標轉換。坐標轉換方法包括直接進行三維坐標轉換[1],以及通過平面坐標轉換[2]和高程擬合[3]來達到三維坐標的轉換。平面坐標轉換的主要方法有四參數模型[4-5]、多項式轉換模型[6]、格網插值[7]等,模型參數解算方法有最小二乘法[8]、總體最小二乘法[8-10]等。
坐標轉換的精度不僅受轉換模型的影響,還與公共點個數和分布、地形情況等因素有關。對于小范圍平坦地區,各模型的轉換精度都較高,而且差異不大[11]。即使在地形起伏較大的小范圍地區,各模型的轉換精度也能達到厘米級,能夠滿足普通工程應用的要求[12-13]。而對于地形起伏較大的大范圍區域,坐標轉換的精度受不同因素的影響較大。本文將探討四參數模型和二次曲面模型在地形起伏較大地區的適用性,以及公共點選取對模型轉換精度的影響。
1 坐標轉換模型
1.1 四參數模型
四參數模型[5,14]是一種相似變換,其計算公式為
(1)
式中,Δx、Δy、θ、m分別為平面上的平移、旋轉、尺度參數。當有兩個以上轉換公共點時,將此模型轉換為線性模型用最小二乘求解,即
(2)
1.2 二次曲面模型
二次多項式擬合[6,15]是多項式變換中的一種,其計算公式為
(3)
式中,a0、a1、a2、a3、a4、a5、b0、b1、b2、b3、b4、b5為轉換參數,當轉換點個數大于6時,可以通過最小二乘法結合線性回歸原理求解轉換參數。
1.3 精度評定
轉換殘差計算公式為:vx=x′-x,vy=y′-y。其中x′、y′為轉換后坐標值,x、y為同名點原坐標值。
坐標分量X、Y轉換中誤差為
計算內符合精度時,n為轉換點個數;計算外符合精度時,n為檢驗點個數。
點位中誤差為
2 試驗區和數據
青海高原地形起伏大,礦山分布較為零散,本文采用的礦業權核查坐標數據范圍大,面積約為4000 km2,共有9個公共點,其中A02和A04的距離最遠,約為108 km。圖1為公共點分布和地形起伏情況。地勢西低東高,海拔最低為3113 m(A08),最高為4261 m(A02),公共點最大高差達1148 m,而且受礦山分布的影響,公共點分布也不均。
3 試驗結果與討論
3.1 兩種模型比較
雖然四參數模型只需要2個公共點即可求解轉換參數,但由于二次曲面模型參數的求解至少需要6個公共點,因此,本文采用3種公共點組合方案對比四參數模型和二次曲面模型的適用性(見表1),其他公共點作為檢驗點,檢驗坐標轉換的外符合精度。
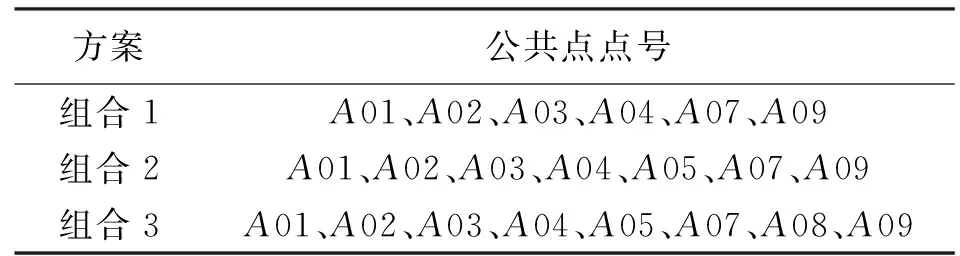
表1 3種公共點組合方案
在組合1的方案中,公共點主要選取的是測區的邊界點(圖2中圓圈點),表2顯示四參數的X、Y分量的內外符合精度在分米至米級(點位中誤差分別為1.362 m和1.262 m),最小絕對偏差為0.136 m(A07),最大絕對誤差達到了1.697 m(A04)。這樣的轉換精度顯然無法滿足高精度工程應用的需要。而二次曲面模型的外符合轉換精度則要高很多,精度為厘米級(點位中誤差為6.8 cm),外符合最大絕對偏差為7.6 cm(A05)。由于6個公共點剛好求解二次曲面模型的轉換參數,沒有多余觀測值,因此其內符合轉換誤差為0。
組合2的方案將區域內部的A05號點納入轉換點中,四參數模型坐標轉換的最小絕對偏差減少至9.1 cm(A07),但是最大絕對偏差卻增加至1.759 m(A04),內外符合的點位中誤差分別為1.291 m和1.476 m。二次曲面模型的外符合精度中最大最小絕對偏差幾乎沒有變化,但坐標轉換的整體精度有所提高,外符合點位中誤差減小至5.5 cm。
組合3的方案將測區內最低點A08(3113 m)納入到轉換點中,四參數模型坐標轉換的外符合精度反而明顯降低,點位中誤差達2.024 m。這說明對于大范圍區域,四參數模型進行坐標轉換的精度不僅受公共點數量和分布的影響,而且地形因素對其也有著明顯的影響。但二次曲面模型的坐標轉換精度,無論是最大絕對偏差還是整體的點位中誤差都有較為明顯的減小。因為用于求解坐標轉換參數的公共點越多,二次曲面模型越能反映測區坐標的差異特征。
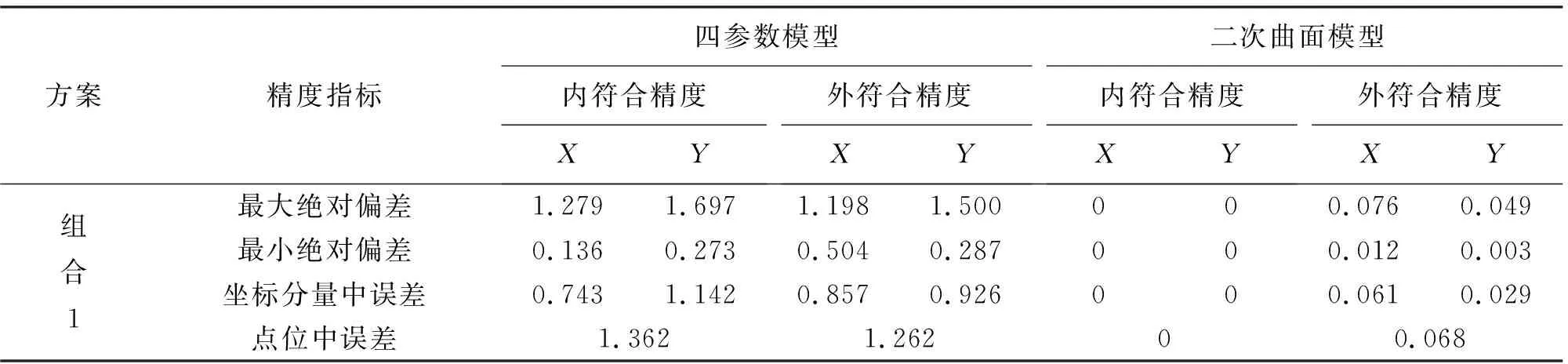
表2 不同組合方案兩種模型的坐標轉換精度統計 m

續表2 m
3.2 二次曲面模型分析
由以上分析可知,二次曲面模型在地形起伏較大的地區適用性更強。為了進一步分析該模型的外推能力,選取不同的公共點進行試驗。圖3(a)和(b)中選取西南角6個公共點點作為轉換點,東北角的A01、A02和A05作為檢驗點進行坐標轉換。從圖中可以看出,檢驗點的轉換精度很差,X分量的誤差超過10 m。由此可見,對于地形起伏大的大范圍區域,二次曲面模型的外推能力很弱。圖3(c)和(d)進一步將最遠、最高的A02納入轉換點中,檢驗點坐標轉換精度有了明顯的提高,處于區域內部的A05號點的轉換精度有了明顯提高,最大偏差為-0.700 m,而處于區域外部的A01號點的最大誤差達到-3.083 m,仍無法用于高精度的工程應用中。這說明將區域邊界的點納入轉換點可以明顯改善區域內部坐標轉換的精度,但區域外部的轉換精度仍較差。圖3(e)和(f)進一步將區域邊界的A01號點納入轉換點中,坐標轉換的內外符合精度均達到了厘米級的精度,最大偏差為7.8 cm。
4 結 論
本文研究了地形起伏大的大范圍區域兩種平面坐標轉換模型的適用性。研究結果表明:
(1) 四參數模型的坐標轉換精度在分米至米級,無法滿足高精度的工程應用需求。受地形因素的影響,納入更多公共點作為轉換點時反而可能會降低坐標轉換的精度。
(2) 當合理選擇轉換點時,二次曲面模型的坐標轉換精度為厘米級,而且增加轉換點的數量可以增加坐標轉換的精度。然而,由于地形起伏較大,該模型的外推能力也很差,因此,通常要選取測區邊界的公共點作為轉換點才能得到較高的坐標轉換精度。

