離散元法用于絞刀齒切削珊瑚礁巖過程的三維模擬

林挺 ，馮沛洪 ，馬源 ，郭濤 *

（1．上海交通大學船舶海洋與建筑工程學院，上海 200030；2．中交疏浚技術裝備國家工程研究中心有限公司，上海 201208）

絞吸挖泥船是一種典型的疏浚工程船，作業時絞刀通過橋架下放到水底，絞刀旋轉并松散、破碎水底的密實砂土或巖體，再由管路、泥泵等輸送系統抽吸、排送砂土、碎巖與水的混合漿體，實現疏浚或吹填的目的。近年來，國內疏浚行業發展迅速且不斷承接國際的港口或海洋工程，沿海疏浚或島礁吹填項目中不乏挖掘珊瑚礁石的工程。未來，水下挖巖的工程量可能進一步增加，設計專用挖掘礁巖、風化巖等巖土的絞刀、刀齒很有必要。

當前，挖巖絞刀的功率預估、結構設計、強度校核主要依靠同類施工經驗，這很可能造成過量設計與匹配浪費，也對新型挖巖絞刀的優化與設計造成了困擾。但是絞刀齒與巖石接觸并破碎巖石的具體受力難以通過絞刀軸上宏觀表現來考察，即使通過物理實驗也難以直接測量，而且物理實驗具有耗時長、費用大等缺陷。

離散元方法（Discrete element method，DEM）源起上世紀70年代，可將物質處理為由不連續的顆粒組成的集合，通過求解各顆粒的運動方程實現模擬物質的運動與變形，是巖土力學領域中的典型數值研究方法[1]，已在海底巖體破碎等研究中得到良好應用[2]。本文將采用DEM三維求解絞刀挖掘珊瑚礁巖時刀齒上的受力情況，為挖巖絞刀的設計提供參考。

1DEM物理模型

處理彈性顆粒球形面的變形時，DEM廣泛采用考慮切向庫倫摩擦力[3]以及回復阻尼系數[4]的Hertz-mindlin模型。該模型中，相互接觸的球面1、球面2因彈性變形而產生的相互作用力為：

式中：Fn、Ft分別為法向力和切向力；E*、G*分別為等效楊氏模量、等效剪切模量；R*為等效半徑；δn、δt分別為兩球面的法向重疊距離與切向重疊距離，即兩球面的球心距離相較于初接觸時刻（此時兩球面點接觸，球面無變形，亦無彈性接觸力）的徑向變化量以及兩球接觸面中點相對于初接觸時的切向變化量；μs為顆粒間的靜摩擦系數。并有：

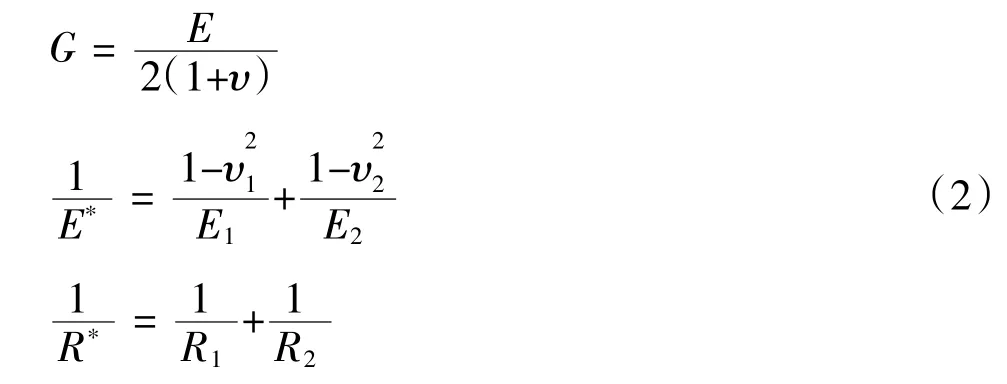
式中：υ為泊松比；其他各字母含義同上，下標1、2分別代表不同球面。可見，兩球面間剪切力的

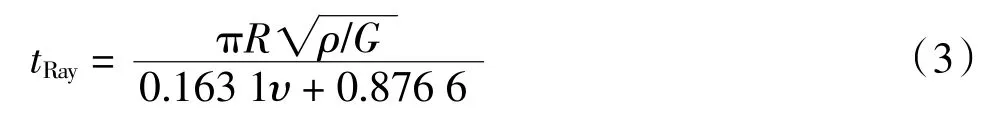
式中：ρ為顆粒密度。實際上對于高配位數的準靜態顆粒堆積（比如三維球形顆粒），通常時間步小于 0．2tRay是合適的。

Hertz-Mindlin模型沒考慮顆粒間的黏聚力，并不適于表征具有黏聚力的巖石類物質。Potyondy與Cundall在此基礎上提出了一種用于巖石的顆粒粘合模型[6]，該模型類似于在相近顆粒之間填充了“固體粘合劑”，可以較大程度上模仿巖石類物質。本文使用該模型來表征珊瑚礁巖中各顆粒間的相互作用。該模型假定在初始時刻，若相鄰離散顆粒的球面中心距離小于接觸半徑Rc，則球面之間將存在一種粘合作用（bonding），本文稱為鍵。鍵的兩端分別為兩球面中心，顆粒發生相對運動時，作用鍵使得球面間存在類似線性彈簧（包括力與轉矩）的相互影響，直到鍵被破壞。鍵對顆粒的作用力變化關系滿足式（4）：

式中：v為顆粒間相對速度；S為單位面積鍵剛度，其量綱為N·m-3；A為鍵的橫截面積；t為時間間隔；下標n、t分別代表法向、切向分量。作用鍵在特定條件下會被破壞而導致“粘合效應”失效，這種破壞不可逆。作用鍵的失效準則包括：鍵上承受了極限法向應力（CNS）、極限切應力（CTS）或者鍵達到極限長度。當存在作用鍵時，時間步長需要考慮鍵力的傳播。

2 珊瑚礁巖的力學性能及DEM模擬參數

珊瑚礁是由珊瑚蟲鈣質遺骸及其他造礁生物的石灰質長期累積而成的巖土體，主體為礁灰巖，在中國南部沿海地區分布廣泛。由于珊瑚蟲種類繁多，珊瑚礁石形成過程中環境不斷變化，礁灰巖的巖體結構復雜，其力學性能也差異明顯。中科院王新志等人[7]曾對永暑礁及渚碧礁的礁灰巖進行了采樣及力學研究，得到礁灰巖力學特性如表1所示[7]。研究中還發現礁灰石內部孔隙率較高，極限不能超過最大靜摩擦力，否則球面間將發生相對滑動或轉動。

為保證計算的準確性，需要確保時間步明顯小于瑞利時間步——剪切波穿過一個顆粒的時間。瑞利時間步 tRay由式（3）[5]確定：干燥礁巖的天然密度約為（1．25～1．35）× 103kg/m3，孔隙率約為45%～55%；礁石壓裂后會存在殘余強度，隨著壓裂破壞的增加強度進一步降低，這與脆性灰巖不同。

表1 采樣礁灰巖力學特性Table 1 The mechanical property of the sampled coral reef rocks

為使DEM模型能夠準確模擬水下飽和珊瑚礁灰巖的力學性能，按DL/T 5368—2007《水電水利工程巖石實驗規程》中的實驗規程，對礁石的巴西劈裂法測抗拉強度實驗以及單軸抗壓強度實驗進行相同的DEM數值實驗，并根據實驗結果調整計算參數。計算中，基本離散粒子選為球形；為保證顆粒直徑總是小于試件直徑的1/10，球形粒徑設為4 mm；接觸半徑為3 mm；為克服球形顆粒易滾動的缺陷，限制顆粒的旋轉自由度；基于Mohr-Coulomb強度理論，假定破碎的主要原因是巖體抗剪切強度不足。

經過多次“選擇參數-計算-修改參數”的循環后，選用表2所示的參數，得到與表1中實驗結果均值相近的礁巖模型。

表2 模擬礁灰巖顆粒參數Table 2 Particle parameters of the simulated coral reef rocks

巴西劈裂法測抗拉強度的實驗中，圓柱形試件的周面上、下兩側各有寬約4 mm的墊條緩慢向內擠壓，圖1給出了實驗前后的鍵變化。圖2給出了實驗中試件承受拉力隨墊條位移的變化過程。圖中可見，礁巖在不足1 mm的變形量下即發生突然的張性斷裂，斷裂面基本經過上下的墊條，其抗拉強度約為1．2 MPa。

圖1 巴西劈裂實驗前、后鍵狀態Fig.1 Statues of the bonds before and after Brazilian splitting test

圖2 巴西劈裂數值實驗計算結果Fig.2 Numerical results of the Brazilian splitting test

圖3給出了礁石單軸抗壓強度實驗前、后的鍵變化。圖4給出了單軸抗壓強度的數值計算結果。從圖中可見，數值模擬的礁巖圓柱在軸向形變約1 mm時達到最大單軸抗壓強度，約為6 MPa。此后壓力隨著軸向形變增大而迅速減少，這點與實驗中壓力階梯式減小的真實情況不符，這可能是數值模擬中忽略了真實礁巖材料內不均勻分布的孔隙所造成的。盡管數值結果在應力衰減上存在偏差，但在極限應力、極限形變上與實驗情況非常相近，仍認為當前計算參數能夠表征珊瑚礁巖的主要力學性能。

圖3 單軸壓裂實驗前、后鍵狀態對比Fig.3 Statues of the bonds before and after uniaxial compression test

圖4 單軸壓裂數值實驗計算結果Fig.4 Numerical results of the uniaxial compression test

3 絞刀齒切珊瑚礁巖的三維計算與分析

絞吸船工作時，橋架上的絞刀探入水下并繞軸旋轉，帶動刀齒、刀臂切削巖土。船體一邊由橫移鋼纜牽動繞工作鋼樁轉動，一邊由臺車推動改變船體與工作鋼樁的距離，同時橋架受巖土的反作用力變化，導致其下探角度略微波動。因考察局部刀齒挖掘過程，絞刀的變半徑、變深度的弧形運動可以近似簡化為繞軸旋轉以及水平橫移的疊加，如圖5所示。

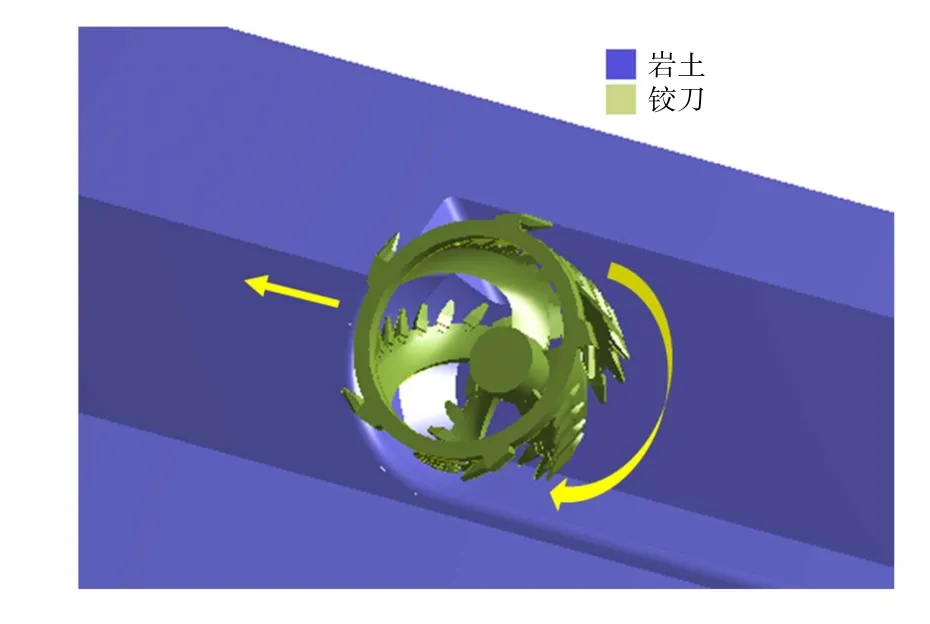
圖5 簡化后絞刀運動示意圖Fig.5 Schematic diagram for the simplified cutter movement

DEM的計算量隨粒子數增加而指數級上升。受限于計算資源，本文僅計算了某大型六臂絞刀的第4排相鄰刀齒以大挖巖橫移速度挖掘礁巖時的受力情況。該絞刀額定功率2 000 kW，最大旋轉半徑約1．74 m。由于安裝半徑、安裝角度不同，不同刀齒的挖掘面積也不同。以本絞刀第4排刀齒為例，其相鄰刀齒錯開排列，齒尖半徑分別為1．232 m與1．309 m，尖端半徑較小的齒（后稱齒A）在軸向上較鄰齒（后稱齒B）前突約0．1 m，相鄰齒尖的周向夾角分別為67°及53°。絞刀旋轉速度22 r/min、橫移速度15 m/min，圖6給出向上挖掘礁巖時相鄰的齒A、齒B受力的計算模型。圖中模型的顆粒數約為85 000個，虛線為齒尖的運動軌跡。由圖可見，受刀齒錯開排列的影響，齒A在橫移面上的挖掘面明顯小于齒B，但齒A在軸向上突前，軸向挖掘深度明顯大于齒B。

圖6 計算刀齒切削過程模型Fig.6 The model for simulating the cutting processes

計算時，先由齒A破環礁巖表面并留下挖掘痕跡，考察后續相鄰的齒B、齒A繼續切削礁巖的受力情況。珊瑚礁巖按圖6中的樣式構建以減少離散粒子數量，礁巖軸向厚度0．28 m，絞刀軸位于礁巖上沿0．7 m。

為了提高計算效率，根據式（1）、（3）、（4）以及相似準則，調整計算參數如表3所示。其他計算設置與前文一致，計算結果與選用表2參數的結果相似，相似比例為1∶1 000，計算耗時為后者的1/30。計算的時間步長為2×10-6s，總時長為1．2 s，使用Intel I7-4790處理器滿負荷計算共耗時約30 h。圖7給出了計算后礁巖的破壞情況。

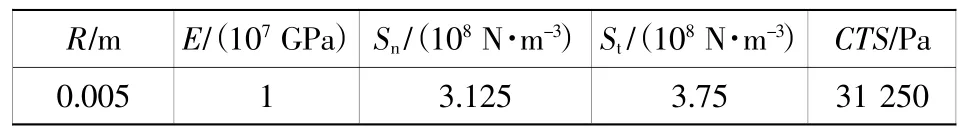
表3 等效計算時選擇的參數設置Table 3 Parameters used in the equivalent calculations

圖7 刀齒切削后礁巖模型Fig.7 The reef model after cutting with cutter teeth

圖7中，礁巖上刀齒所過處礁巖破裂，部分碎裂成粒子，部分仍保持團塊狀，刀齒未經過處的內部也存在著明顯裂痕。在頂部，齒A在軸向上基本挖穿了礁巖；在底部，齒B的挖掘深度約為齒A的一半。

設定齒B在挖掘起點處為絞刀的0°相位角，相位角將隨著絞刀旋轉而增加。圖8給出了計算得到的齒A與其相鄰的齒B在挖掘過程中所承受的礁巖作用力隨絞刀旋轉的變化。

從圖中可見，齒A與齒B上承受的峰值力分別約為5×104N與9×104N。齒B上承受了較高的作用力，這是由于齒B旋轉半徑較大，齒A切削范圍內的部分礁巖顆粒已被齒B破壞了內部鍵。

圖8 刀齒上切削合力隨相位角變化Fig.8 Cutting forces on the teeth vary with rotating anlges

假設絞刀第4排的3對A、B齒在挖掘過程的受力情況相同，根據刀齒受力矢量和相對位置可以折算出該排刀齒整體所受的挖掘力矩，該值以120°為周期往復性變化。圖9給出了2個周期內的估算力矩及擬合曲線。可見，絞刀第4排刀齒承受的力矩大致在（1～9）×104N·m的范圍內，在齒B開始切削后又旋轉了約42°時達到最大值，在齒A完成切削時達到最小值。

圖9 第4排刀齒挖掘力矩隨相位角變化Fig.9 The cutting torque of the fourth row teeth vary with rotating anlges

圖8中，刀齒B在相位角約為40°～50°時受力最大，計算此時間段內的刀齒表面承受壓力的時均值，采用插值映射的方法將該值作為刀齒載荷施加在有限元軟件上，考察作用力可能引起的刀齒應力分布及變形。刀齒材料選擇為某低合金耐磨鋼，計算結果如圖10、圖11所示。圖中，礁巖對刀齒的壓力主要集中在齒尖上，在齒B承受最大受力時，齒尖壓力峰值高達1．14×108Pa。此時，齒尖處將發生最大約0．54 mm的變形，齒背上加強筋處的von-Mises等效應力最大，約1．68×108Pa，同理此處的安全系數最小，約為7．1。

圖10 刀齒最大受力時的變形Fig.10 The deformation of the cutter teeth under maximum force

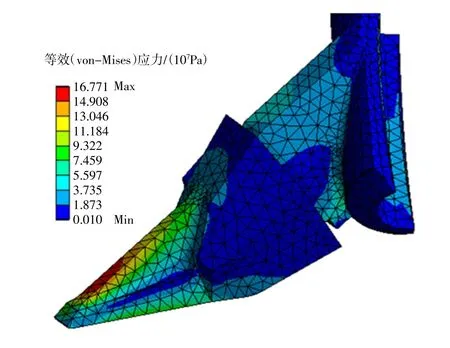
圖11 刀齒承受的最大等效應力Fig.11 The maximum equivalent stress on the cutter teeth

4 總結與討論

使用DEM三維模擬了絞刀第4排刀齒挖掘珊瑚礁巖的過程，量化求解了挖巖機具的受力情況，并對計算結果進行了有限元分析，為挖巖絞刀或類似機械的設計、校核與優化提供了一種數值解決方案，得到以下結論：

1）Hertz-Mindlin接觸模型與顆粒粘合模型，可以更有效地模擬珊瑚礁巖等巖體的內聚力效應，模擬結果更接近真實情況。

2）本文確定的DEM參數可以較準確地表征珊瑚礁巖的力學性能，并能較高效地處理絞刀挖掘礁巖的受力、破碎問題。

3）計算的刀齒挖掘礁巖時的最大受力約為9×104N，最大等效應力約為 1．68×108Pa，佐證了該刀齒的結構設計與安裝角度滿足挖掘礁巖的強度要求。

受限于資源耗費與計算效率，本文在顆粒形狀、粒子尺度、粒子參數、模型范圍等方面尚有不足，例如未使用不同形狀、非均勻粒徑的粒子以及非均勻的鍵值等方式來模擬礁巖內的裂隙現象，進一步研究工作可在這方面做出改善，實現更高精度的計算，并推廣到整個絞刀挖巖過程的模擬。