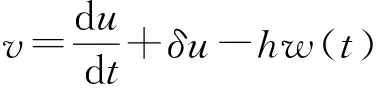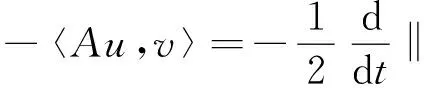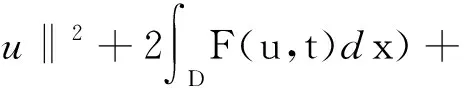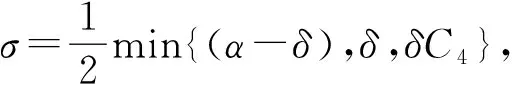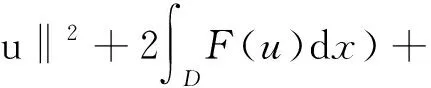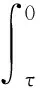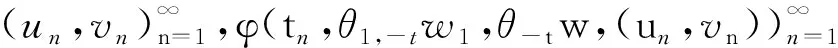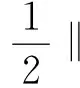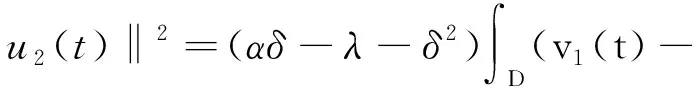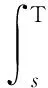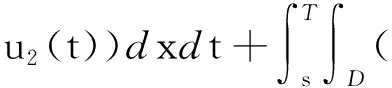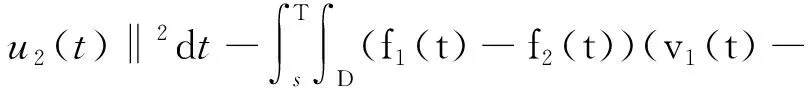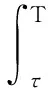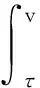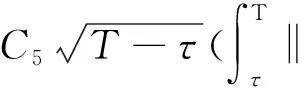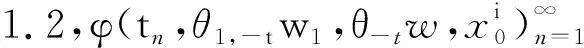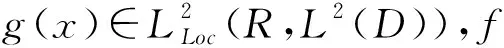一類非自治隨機波動方程的隨機吸引子

文慧霞, 舒 級, 李林芳

(四川師范大學 數(shù)學與軟件科學學院, 四川 成都 610066)

1 引言及預備知識

設D?R3為具有光滑邊界的有界區(qū)域，本文在D上考慮如下具加性噪聲的非自治隨機波動方程的長時間漸近行為

utt+αut-Δu+λu+f(u,t)=g(x,t)+

(1)

初邊值條件為

u(x,τ)=u0(x),

ut(x,τ)=u1(x), x∈D,

(2)

u(x,t)=0, x∈?D,t≥τ,

(3)

其中,α、λ是正常數(shù)，τ表示初始時刻，Δ是Laplace算子,w是一維雙邊標準Wiener過程，g(x,t)是時間依賴的外力項，非線性項f為R上光滑的具有立方增長率的函數(shù).

波動方程是一類非常重要的偏微分方程,在物理學、流體力學、聲學、電動力學等眾多領域應用廣泛.文獻[1-4]對自治的隨機波動方程證明了隨機吸引子的存在性,文獻[5-6]提出了壓縮函數(shù)方法用于證明非自治系統(tǒng)的漸近緊性,文獻[7-8]考慮了具可乘白噪音的非自治波動方程的漸近行為,文獻[9]對有界區(qū)域上的非自治隨機波動方程證明了隨機吸引子的存在性.

隨機吸引子是研究隨機動力系統(tǒng)長時間漸近行為的有效工具，其實質(zhì)是緊的不變集，該不變集依概率并隨著時間變化.隨機吸引子是對確定性動力系統(tǒng)中吸引子的推廣[10].文獻[11-12]給出了隨機動力系統(tǒng)中隨機吸引子的概念，并在文獻[13-14]中作了詳細闡述;文獻[15]給出了對非自治無窮維動力系統(tǒng)和隨機動力系統(tǒng)漸近行為的具體研究;文獻[16-18]討論了自治與非自治的反應擴散方程隨機吸引子的相關問題;文獻[19-20]則關注了格上的隨機動力系統(tǒng)的漸近性質(zhì);文獻[21-23]討論了隨機廣義Ginzburg-Landau方程的漸近行為;文獻[24-25]給出了一些KdV型方程隨機吸引子的存在性證明.

本文的目的是證明(1)～(3)式在D上存在拉回吸引子.應用類似于文獻[1-6]中的方法來解決這個問題.

下面給出非自治隨機動力系統(tǒng)和隨機吸引子的有關知識，具體參見文獻[8,11,13].首先引進一些記號，用‖·‖和(·,·)表示Hilbert空間L2(D)的范數(shù)和內(nèi)積.假設(X,‖·‖)是一個可分度量空間,B(X)為X的Borelσ-代數(shù).

定義1.1設Ω是一個非空集合.如果一個映射θ:R×Ω→Ω滿足:

(i)θ(0,·)為在Ω上的恒等映射IΩ;

(ii)θ(t+s,ω)=θ(t,θ(s,ω)),?s,t∈R,ω∈Ω;

稱θ為Ω上的一個動力系統(tǒng).

定義1.2設θ1,θ2,,θr分別為集合Ω1,Ω2,,Ωr上的動力系統(tǒng)，X為一個拓撲空間.如果一個映射φ:R+×Ω1×Ω2××Ωr×X→X滿足：

(i)φ(0,ω1,ω2,,ωr,x)=x,?(ω1,ω2,,ωr)∈Ω1,Ω2,,Ωr;

(ii) 對?s,t∈R,(ω1,ω2,,ωr)∈Ω1,Ω2,,Ωr,x∈X有

φ(t+s,ω1,ω2,,ωr,x)=φ(t,θ1(s,ω1),,

θr(s,ωr),φ(ω1,ω2,,ωr,x));

(iii) 對?s,t∈R,(ω1,ω2,,ωr)∈Ω1,Ω2,,Ωr,x∈X,φ(t+s,ω1,ω2,,ωr,·)在X中連續(xù),

則稱φ為在X上的具有r個參數(shù)(ω1,ω2,,ωr)的關于參數(shù)動力系統(tǒng)θ1,θ2,,θr的動力系統(tǒng).把Ωi(i=1,2,,r)叫做參數(shù)空間,(Ωi,θi)(i=1,2,,r)叫做參數(shù)動力系統(tǒng).

對一個參數(shù)為隨機參數(shù)的具有2個參數(shù)的動力系統(tǒng)，設(Ω2,F,P)是一個概率空間，保測映射φ2:R×Ω2→Ω2是一個關于σ-代數(shù)B(R×F;F)可測動力系統(tǒng)，即?t∈R,P·θ2,t=P.動力系統(tǒng)(Ω2,θ2)叫做隨機參數(shù)動力系統(tǒng).設(Ω1,θ1)為任意一個隨機參數(shù)動力系統(tǒng).一個動力系統(tǒng)φ:R+×Ω1×Ω2×X→X,如果對?ω1∈Ω1,φ(·,ω,·,·)關于(B(R+)×F×B(X);B(X))是可測映射，則稱φ為隨機動力系統(tǒng).

定義1.3如果X的一個集族K=K(ω1,ω2):Ω1×Ω2→2X,(ω1,ω2)aK(ω1,ω2),對?ω1∈Ω1,x∈X,映射ω2→(x,K(ω1,ω2))關于σ-代數(shù)(F;B(R+))是可測的，則稱K為隨機集族.

定義1.4稱一個非空集族A=A(ω1,ω2)為隨機動力系統(tǒng)φ的拉回吸收集.如果對任意有界集B?X,ω1∈Ω1,以及P-a.s.ω2∈Ω2,存在T=T(ω1,ω2;B)≥T時有

φ(t,θ1,-t(ω1),θ2,-t(ω2),B)?A(ω1,ω2),

其中,dist(·,·)表示X中的Hausdoff半度量.

定義1.5稱一個非空集族A=A(ω1,ω2)關于φ的拉回吸引有界集B?X,如果對?ω1∈Ω1,以及P-a.s.ω2∈Ω2有

A(ω1,ω2))=0.

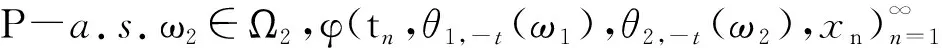
定義1.7如果一個隨機緊集A=A(ω1,ω2)，對?ω1∈ω1,以及P-a.s.ω2∈ω2滿足:

(i)A關于φ拉回吸引X的任意有界閉集；

(ii)A關于φ隨機不變集,也就是說，對?t≥0,

φ(t,ω1,ω2,A(ω1,ω2))=

A(θ1,t(ω1),θ2,t(ω2)),

則稱A為隨機動力系統(tǒng)φ的一個隨機吸引子.

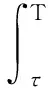
定理1.1[26]定義于度量空間X上的連續(xù)隨機動力系統(tǒng)φ，如果存在一個拉回吸收集B(ω1,ω2)，且φ在X中是漸近緊，那么φ擁有唯一的拉回吸引子A=A(ω1,ω2)為

A(ω1,ω2)=

定理1.2[5] 設定義于度量空間X上的連續(xù)隨機動力系統(tǒng)φ存在一個拉回吸收集B(ω1,ω2)，對?ε>0,ω1∈Ω1，以及P-a.s.ω2∈Ω2,存在T=T(ω1,ω2,ε)>0和壓縮函數(shù)ψT，對?(x,y)∈B(θ1,-t(ω1),θ2,-t(ω2))，當T

‖φ(T,θ1,-t(ω1),θ2,-t(ω2),x)-

φ(T,θ1,-t(ω1),θ2,-t(ω2),y)‖≤ε+ψT(x,y),

2 帶加性噪聲的非自治隨機波動方程

由于w為完備概率空間(Ω2,F,P)中的一個獨立雙邊實值Wiener過程，其軌道w(·)屬于C(R,R)，且w(0)=0，在(Ω2,F,P)中的保測度轉(zhuǎn)移算子定義為

θtw(·)=w(·,+t)-w(t),

w∈Ω2, t,s∈R,

那么(Ω2,F,P,(θt)t∈R)為一個度量動力系統(tǒng).

對一較小的正數(shù)δ，引進新的變量z=ut+δu和v(t)=z(t)-hw(t),于是方程(1)～(3)變?yōu)橹缓S機參數(shù)的隨機方程

(4)

其中，A=-Δ，v0=z0-hw(t)，z0=u1+δu0，x∈D.

為了得到方程弱解的存在性和拉回吸引子的存在性，需要對非線性項f施加條件：f∈C1(R×R,R)，并假設存在正常數(shù)C1,C2,C3,C4>0,對?u∈R,t∈R滿足:

|f(u,t)|≤C1(1+|u|3),

(5)

|f′(u,t)|≤C2(1+|u|2),

互聯(lián)網(wǎng)時代，資源共享已經(jīng)成為人們的共識，在此背景下，教師可以很輕松地通過網(wǎng)絡搜索優(yōu)秀的教案、課件和教學日志來完成備課，甚至還可以通過網(wǎng)絡視頻觀看和學習其他優(yōu)秀教師的教學方法。這就是“互聯(lián)網(wǎng)+”時代資源共享給我們帶來的好處。然而，有的教師卻只會盲目照搬照抄這些網(wǎng)絡教學資源，有的教師在教學過程中，離開信息技術無法上課，到了依賴的地步，把大量的時間和精力花費在對網(wǎng)絡教育資源的收集和模仿上，從而喪失了自身獨立思考和研究的能力，以至于成為信息技術的傳話筒。這種忽視學生實際情況和教學環(huán)境的方式，不僅不能發(fā)揮出網(wǎng)絡教育資源應有的作用，甚至還有可能起到反效果。

(6)

F(u,t)≥C3(|u|4-1),

(7)

uf(u,t)≥C4(F(u,t)-1),

(8)

θ1,t(f(·),g(·))=(f(t+·),g(t+·)),

t∈R,w1=(f,g)∈Ω1.

類似參考文獻[10]中第IV章中定理5.1的證明，可得到如下定理.

注意，當選取δ滿足λ+δ2-αδ≥0時，這一范數(shù)與如下范數(shù)是等價的

‖(u,v)‖X=(‖▽u‖2+

(9)

那么，在X上定義隨機動力過程為φ(t,θ1,τw1,θτw,x0)=(u(t),v)∈X,u(t)是方程(4)中初始時間為τ的在τ+t時刻的解,其中w1(f(t),g(t))∈Ω1,w∈Ω2,x0=(u0,v0)∈X,那么由定理2.1可知，φ在X中關于參數(shù)動力系統(tǒng)θ1和θ構成隨機動力系統(tǒng).

3 隨機吸引子的存在性

為了證明隨機吸引子的存在性，首先給出解的先驗估計，得到X中的隨機吸收集.

引理3.1在定理2.1的假設條件下，隨機動力過程φ在相空間X上存在隨機吸收集.

證明這里需要估計

‖φ(t,θ1,τw1,θτw,x0)‖X

的值.為此，取w1=(f(u,t+τ),g(x,t+τ)).將方程(4)兩邊與v做內(nèi)積得到

(δ-α)〈v,v〉+〈g(x,t),v〉-〈f(u,t),v〉+

(δ-α)〈h,v〉w(t).

(10)

δ‖u‖2-〈h,u〉w(t),

(11)

δ‖▽u‖2+〈▽h,▽u〉w(t),

(12)

δ〈f(u,t),u〉+〈f(u,t),h〉w(t),

(13)

則方程(10)變?yōu)?/p>

2(α-δ)‖v‖2+2δ(λ+δ2-αδ)‖u‖2+

2δ‖▽u‖2+2δ〈f(u,t),u〉=

2(λ+δ2-αδ)〈h,u〉w(t)+2〈▽u,▽h〉w(t)+

2〈f(u,t),h〉w(t)+2〈g,v〉+

2(δ-α)〈h,v〉w(t).

(14)

由(8)式可得

2δ〈f(u,t),u〉≥

(15)

由(5)與(7)式可得

2C1‖h‖|w(t)|+

2C1‖h‖|w(t)|+

(16)

利用Young和Holder不等式處理余下幾項可得

2(λ+δ2-αδ)〈h,u〉w(t)≤

(λ+δ2-αδ)‖u‖2+

C‖h‖2|w(t)|2,

(17)

2〈▽u,▽h〉w(t)≤δ‖▽u‖2+

C‖▽h‖2|w(t)|2,

(18)

2|〈g,v〉|+2|(δ-α)〈h,v〉w(t)|≤

(α-δ)‖v‖2+C‖h‖2|w(t)|2+

C‖g‖2.

(19)

C3(2σ-δC4)|D|.

(20)

由(8)式得

▽u‖2+

σ(‖v‖2+(λ+δ2-αδ)‖u‖2)≤

C(1+|w(t)|2+|w(t)|4).

(21)

由Gronwall不等式可得

‖v(0,τ,w)‖2+(λ+δ2-αδ)‖u(0,τ,w)‖2+

(λ+δ2-αδ)‖u‖2+‖▽u‖2)ds≤

eστ(‖v0‖2+(λ+δ2-αδ)‖u0‖2+

|w(s)|4)ds.

(22)

由范數(shù)‖·‖X的等價定義(9)式,綜合(7)式得

‖φ(t,θ1,τw1,θτw,x0)‖X≤eστ(‖v0‖2+

(λ+δ2-αδ)‖u0‖2+‖▽u0‖2+

|w(s)|4)ds+C|D|.

(23)

于是當-t→0即τ→-∞時，上式右端第一項趨近于0.又因為w(t)至多多項式增長，所以上式右端第二項有界.令

|w(s)|4)ds+C|D|,

那么從(23)式可知，隨機集

B(w1,w)={x∈X,‖x‖X≤R(w1,w)}

是φ的一個拉回吸收集.進一步，有下面的漸近緊性.

u2(t))+(Δu1(t)-δu2(t))+(δ-α)(v1(t)-

v2(t))-(f1(t)-f2(t)).

(24)

定義能量函數(shù)為

用v1(t)-v2(t)對上式兩端做內(nèi)積，由

可得

▽u1(t)-

v2(t))(u1(t)-u2(t))dx-δ‖▽u1(t)-

▽u2(t)‖2+〈▽u1(t)-▽u2(t),▽h〉w(t)+

(δ-α)〈v1(t)-v2(t),v1(t)-v2(t)〉-

〈f1(t)-f2(t),v1(t)-v2(t)〉.

(25)

對(25)式t在[s,T]上積分

又因為E0(T)≥0，所以

v2(t))dxdt+Ew(s).

(27)

用u1(t)-u2(t)乘(24)式兩端，并在[τ,T]×D上積分得

(δ-α)(v1(t)-v2(t))(u1(t)-u2(t))-

(f1(t)-f2(t))(u1(t)-u2(t)))dxdt.

(28)

對(26)式關于s在[τ,T]上積分可得

(T-τ)E0(T)=

(v1(t)-v2(t))(u1(t)-u2(t))+

(▽u1(t)-▽u2(t))▽hw(t)]dx+

(δ-α)‖v1(t)-v2(t)‖2-

δ‖▽u1(t)-▽u2(t)‖2-

(29)

結合(27)～(29)式可得

(v1(t)-v2(t))(u1(t)-u2(t))+

(▽u1(t)-▽u2(t))▽hw(t)]dx+

(δ-α)‖v1(t)-v2(t)‖2-

δ‖▽u1(t)-▽u2(t)‖2-

(v1(t)-v2(t))(u1(t)-u2(t))dxdt+

(v1(t)-v2(t))(u1(t)-u2(t))+

‖▽u1(t)-▽u2(t)‖‖▽hw(t)‖]dx+

(δ-α)‖v1(t)-v2(t)‖2)dtds+

(v1(t)-v2(t))(u1(t)-u2(t))dxdt+

上式右端除了最后2行其余部分定義為壓縮函數(shù)ψT，則有

于是，對任意的ε>0，存在充分大的T-τ，使得

‖(un(t),vn(t))‖X<+∞,

?t∈[τ,∞), n∈N.

由弱拓撲的緊性，得到

un?u在L∞([τ,∞);H01(D))中弱*收斂，

vn?v在L∞([τ,∞);L2(D))中弱*收斂，

un→u在L2([τ,∞);L2(D))中強收斂，

un(τ)→u0,un(T)→u(T)在L4中強收斂. (30)

因此，unt=vn-δun+hw(t)在L∞([τ,∞);L2(D))中弱收斂于ut=v-δu+hw(t)，從(30)式中可知

(u1(T)-u2(T))dx=0,

(unt(t)-umt(t))dx=0,

(un(t)-um(t))dx=0.

利用非線性條件(6)和(7)式得

(unt(t)-umt(t))dxdt=

其中

由(7)和(30)式可得

所以可得

(un(t)-um(t))dxdt=0.

又利用柯西不等式，存在一個常數(shù)C5,

▽u1(t)-▽u2(t)‖×

‖▽hw(t)‖dtds≤

從而得

▽u1(t)-

▽u2(t)‖‖▽hw(t)‖dtds=0.

同樣也可找到一個合適的常數(shù)C6,

所以有

‖v1(t)-v2(t)‖2dtds=0.

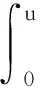
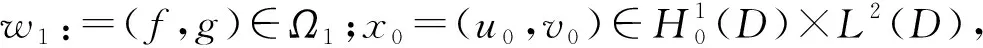
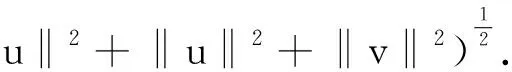
最后，結合定理1.1、引理3.1和引理3.2，可得隨機吸引子的存在性.