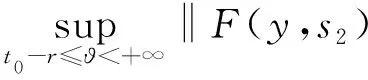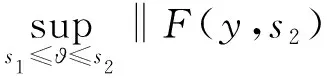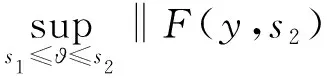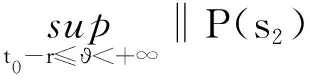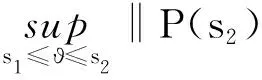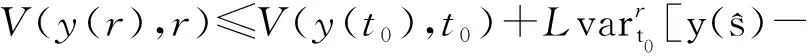滯后型測度泛函微分方程的變差穩定性

李寶麟, 劉靜芳

(西北師范大學 數學與統計學院, 甘肅 蘭州 730070)

當常微分方程

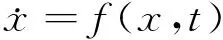
所描述的系統受到擾動時,對受擾動系統導出的常微分方程的形式為

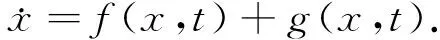
如果擾動項是連續可積的,那么擾動后的系統仍然為常微分方程系統,它的解為連續的.若擾動為脈沖型的,則擾動后系統的狀態就不隨時間連續變化,而是呈現一種瞬時性態.對這種數學模型的研究導出另一類方程即測度微分方程,其一般形式為

Dx=f(x,t)+g(x,t)Du.

(1)

Dy=f(yt,t)Dg

(2)

和它所描述的系統受到擾動后的滯后型測度泛函微分方程

Dy=f(yt,t)Dg+p(t)Du,

(3)

并定義了滯后型測度泛函微分方程的積分穩定性與廣義常微分方程的正則穩定性,證明了滯后型測度泛函微分方程的積分穩定性等價于廣義常微分方程的正則穩定性.在(2)和(3)式中,Dy、Dg、Du分別是y、g、u的分布導數,f:S×[t0,+∞)→Rn,g,u:[t0,+∞)→R,y:[t0-r,+∞)→Rn,yt(θ)=y(t+θ),θ∈[-r,0],r>0,p:[t0,+∞)→Rn,且

S={yt:y∈O,t∈[t0,+∞)}?G*([-r,0],Rn),

O?G*([t0-r,+∞),Rn), r>0.

上述的O為開集,G*([t0-r,+∞),Rn)表示[t0-r,+∞)到Rn所有的有界正則函數全體.由文獻[9]知,方程(2)等價于積分方程

t∈[t0,+∞);

(4)

方程(3)等價于積分方程

(5)

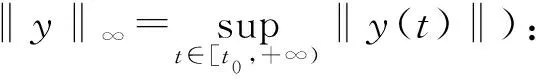
(H2) 對任意的y∈O,s1,s2∈[t0,+∞),存在常數M>0,使得

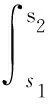
(H3) 對任意的y,z∈O,s1,s2∈[t0,+∞),存在常數N>0,使得

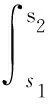
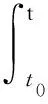
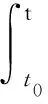
(H5) 對任意的t∈[t0,+∞),s1,s2∈[t0,+∞),存在常數K>0,使得

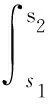
受到以上工作的啟示,本文利用廣義常微分方程的穩定性理論研究滯后型測度泛函微分方程(2)和(3)的變差穩定性和變差漸近穩定性.

1 預備知識

下面主要介紹廣義常微分方程與滯后型測度泛函微分方程的相關概念及其引理.

定義1.1[3]給定一個函數δ(t):[a,b]→(0,+∞),對區間[a,b]上的一個分劃

D:a=α0<α1<<αk=b,

如果有

[αi-1,αi]?[τ-α(τi),τ+α(τi)], i=1,2,,k,

稱分劃D為[a,b]上的δ-精細分劃.

定義1.2[3]設函數U:[a,b]×[a,b]→Rn,如果存在I∈Rn,使得對任意的ε>0,存在正值函數δ:[a,b]→(0,+∞),且對[a,b]上的任何的δ-精細分劃

D={(τj,[αi-1,αi]),j=1,2,,k},

其中

τj∈[αi-1,αi]?[τj-δ(τj),τj+δ(τj)],

有

稱函數U:[a,b]×[a,b]→Rn在[a,b]上為Henstock-Kurzweil可積的.此時記作

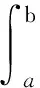
設G:Ω→Rn,Ω=O×[t0,+∞).

定義1.3[3]設函數G:Ω→Rn,如果對所有的t∈[α,β],(x(t),t)∈Ω,任意的s1,s2∈[α,β],有等式

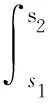
成立,則稱x:[α,β]→Rn是廣義常微分方程

在區間[α,β]?[t0,+∞)上的解.

定義1.4[9]設不減函數h:[t0,+∞)→R,如果函數G:Ω→Rn滿足:對任意的(x,s1),(x,s2)∈Ω,有

‖G(x,s2)-G(x,s1)‖∞≤|h(s2)-h(s1)|;

對任意的(x,s1),(x,s2),(y,s1),(y,s2)∈Ω,有

‖G(x,s2)-G(x,s1)-G(y,s2)+G(y,s1)‖∞≤

‖y-z‖∞|h(s2)-h(s1)|,

則函數G屬于函數族F(Ω,h).

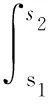
引理1.1[9]設f:S×[t0,+∞)→Rn滿足(H1)～(H3),函數g:[t0,+∞)→R為不減的,對于y∈O,t∈[t0,+∞),定義如下函數

F(y,t)(?)=

(6)

則F∈F(Ω,h),其中

F:O×[t0,+∞)→G*([t0-r,+∞),Rn).

引理1.2[9]考慮廣義常微分方程

(7)

其中F由(6)式給定,函數h:[t0,+∞)→R定義如下

h(t)=(M+N)[g(t)-g(t0)],

t∈[t0,+∞),

(8)

則由h定義可知h為[t0,+∞)上不減的左連續函數.

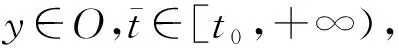
引理1.3[9]設O是G*([t0-r,+∞),Rn)的開子集,且t∈[t0,+∞)時,具有延拓性質,S={yt:y∈O,t∈[t0,+∞)},φ∈S,g:[t0,+∞)→R是不減函數,f:S×[t0,+∞)→Rn滿足條件(H1)～(H3).

(i) 假設對于任意的y∈O,t∈[t0,+∞).如果y:[t0-r,+∞)→O是滯后型測度泛函微分方程

的解.

對任意的t∈[t0-r,+∞),有

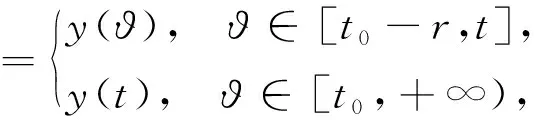
則函數x:[t0,+∞)→O是廣義常微分方程

在初值條件

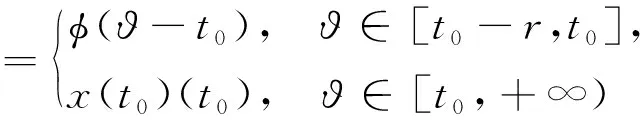
下的解,其中F由(6)式給定.

(ii) 相反地,F由(6)式給定,如果x:[t0,+∞)→O是廣義常微分方程

的解,且滿足初值條件

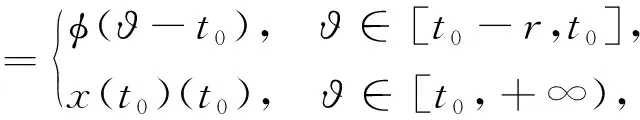
則函數y:[t0-r,+∞)→O是滯后型測度泛函微分方程

在初值條件

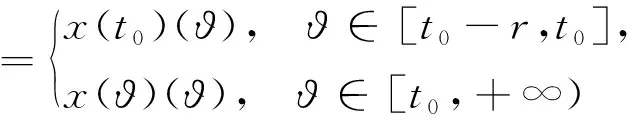
下的解.

引理1.4[9]設f:S×[t0,+∞)→Rn滿足(H1)～(H3),且p:[t0,+∞)→Rn滿足(H4)和(H5),函數g,u:[t0,+∞)→R為不減的,對于y∈O,t∈[t0,+∞),定義如下函數

F(y,t)(?)=

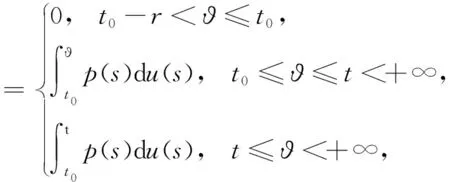
則有

G(y,t)=F(y,t)+P(t),

(9)

且G∈F(Ω,h),其中

G:O×[t0,+∞)→G*([t0-r,+∞),Rn).

引理1.5[9]考慮廣義常微分方程

(10)

其中G由(9)式給定,函數h1,h2:[t0,+∞)→R,有如下定義

h1(t)=(M+N)[g(t)-g(t0)],

h2(t)=K[u(t)-u(t0)],

t∈[t0,+∞).

(11)

定義h:[t0,+∞)→R如下

h(t)=h1(t)+h2(t),t∈[t0,+∞),

則由定義可知h1、h2、h為[t0,+∞)上不減的左連續函數.

引理1.6[9]設O是G*([t0-r,+∞),Rn)的開子集,且t≥t0時,具有延拓性質,S={yt:y∈O,t∈[t0,+∞)},φ∈S,u,g:[t0,+∞)→R是不減函數,f:S×[t0,+∞)→Rn滿足條件(H1)～(H3),且p:[t0,+∞)→Rn滿足(H4)和(H5).

(i) 假設對于任意的y∈O,t∈[t0,+∞),如果y:[t0-r,+∞)→O是滯后型測度泛函微分方程

的解.

對任意的t∈[t0-r,+∞)有

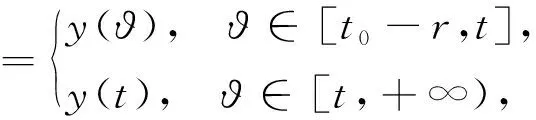
則函數x:[t0,+∞)→O是廣義常微分方程

在初值條件

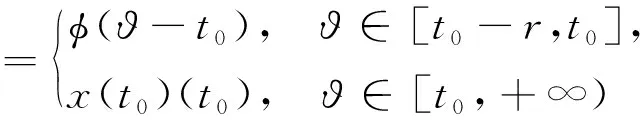
下的解,G由(9)式給定.

(ii)相反地,G由(9)式給定,如果x:[t0,+∞)→O是廣義常微分方程

的解,且滿足初值條件

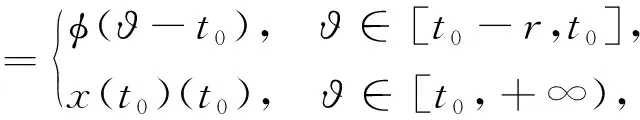
則函數y:[t0-r,+∞)→O是滯后型測度泛函微分方程

在初值條件

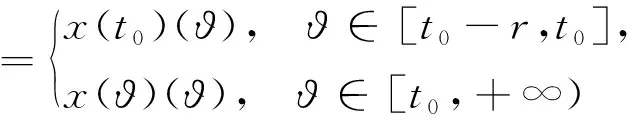
下的解.

引理1.7[3]設V:Rn×[0,+∞)→R,對于任意的y∈Rn,函數V(y,·):[0,+∞)→R在區間(0,+∞)上是左連續的,假設以下條件成立:

(i) 對于任意的(x,t),(y,t)∈Rn×[0,+∞),常數L>0,有

|V(x,t)-V(y,t)|≤L‖x-y‖∞;

(ii) 存在一個實函數Φ:Rn→R,使得對于滯后型測度泛函微分方程(2)在區間[t0,+∞)?[0,+∞)上的每一個解y:[t0,+∞)→Rn,對t∈[t0,+∞)有

Φ(y(t));

(12)

如果

y:[t0,t1]→Rn, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,則不等式

V(y(t1),t1)≤V(y(t0),t0)+

(13)

成立,其中

F由(6)式給定.

引理1.8[3]設V:Rn×[0,+∞)→R,對于任意的y∈Rn,函數V(y,·):[0,+∞)→R在區間(0,+∞)上是左連續的,假設以下條件成立：

(i) 對于任意的(x,t),(y,t)∈Rn×[0,+∞),常數L>0,有

|V(x,t)-V(y,t)|≤L‖x-y‖∞;

(ii) 存在一個實函數Φ:Rn→R,使得對于滯后型測度泛函微分方程(3)在區間[t0,+∞)?[0,+∞)上的每一個解y:(t0,+∞)→Rn,對t∈(t0,+∞)有

Φ(y(t));

(14)

如果

y:[t0,t1]→Rn, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,則不等式

V(y(t1),t1)≤V(y(t0),t0)+

(15)

成立,其中

G由(9)式給定.

2 主要結果

下面主要討論滯后型測度泛函微分方程(2)與受到擾動后的滯后型測度泛函微分方程(3)的變差穩定性與變差漸近穩定性,利用廣義常微分方程的穩定性理論給出滯后型測度泛函微分方程的變差穩定性定理及其證明.

定義2.1如果對于任意的ε>0,存在δ=δ(ε)>0,使得若

y:[t0,t1]→O, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,當‖y(t0)‖∞<δ和

(16)

其中F由(6)式給定.對于任意的t∈[t0,t1],有‖y(t)‖∞<ε,則稱滯后型測度泛函微分方程(2)的解y≡0是變差穩定的.

定義2.2如果存在δ0>0,對于任意的ε>0,有T=T(ε)≥0和γ=γ(ε)>0,使得若

y:[t0,t1]→O, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,當‖y(t0)‖∞<δ0和

(17)

其中F由(6)式給定.對于任意的t∈[t0,t1]∩[t0+T(ε),+∞),且t0≥0時,有‖y(t)‖∞<ε,則稱滯后型測度泛函微分方程(2)的解y≡0是變差吸引的.

定義2.3如果滯后型測度泛函微分方程(2)的解既是變差穩定的,又是變差吸引的,則稱滯后型測度泛函微分方程(2)的解是y≡0是變差漸近穩定的.

定義2.4如果對于任意的ε>0,存在δ=δ(ε)>0,使得若

y:[t0,t1]→O, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,當‖y(t0)‖∞<δ和

(18)

其中G由(9)式給定.對于任意的t∈[t0,t1],有‖y(t)‖∞<ε,則稱滯后型測度泛函微分方程(3)的解y≡0是變差穩定的.

定義2.5如果存在δ0>0,對于任意的ε>0,有T=T(ε)≥0和γ=γ(ε)>0,使得若

y:[t0,t1]→O, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,當‖y(t0)‖∞<δ0和

(19)

其中G由(9)式給定.對于任意的t∈[t0,t1]∩[t0+T(ε),+∞),且t0≥0時,有‖y(t)‖∞<ε,則稱滯后型測度泛函微分方程(3)的解y≡0是變差吸引的.

定義2.6如果滯后型測度泛函微分方程(3)的解既是變差穩定的,又是變差吸引的,則稱滯后型測度泛函微分方程(3)的解是y≡0是變差漸近穩定的.

定理2.1設V:O×[0,+∞)→R,使得對于任意的y∈O?G*([t0-r,+∞),Rn),r>0,函數V(y,·):[0,+∞)→R在區間(0,+∞)上是左連續的.假設V(y,·)是正定的,即存在一個連續遞增實函數b:[0,+∞)→R,使得b(ρ)=0當且僅當ρ=0,對所有的(y,t)∈O×[0,+∞),任意的x∈O,常數L>0,有:

V(y,t)≥b(‖y‖∞),

(20)

V(0,t)=0,

(21)

和

|V(x,t)-V(y,t)|≤L‖x-y‖∞.

(22)

如果函數V(y(t),t)對滯后型測度泛函微分方程(2)的任何一個解y(t)是不增函數,則方程(2)的平凡解y≡0是變差穩定的.

證明由引理1.1,驗證F∈F(Ω,h),Ω=O×[t0,+∞).由假設存在常數M、N,對于任意的y,z∈O,條件(H1)暗示了在F的定義下積分存在,給定y∈O,且0≤t0

F(y,s2)(?)-F(y,s1)(?)=

則由條件(H2)有

‖F(y,s2)(?)-F(y,s1)(?)‖∞=

M[g(s2)-g(s1)]≤h(s2)-h(s1),

由條件(H3)有

‖F(y,s2)(?)-F(y,s1)(?)-

F(z,s2)(?)+F(z,s1)(?)‖∞=

‖y-z‖∞[h(s2)-h(s1)].

由引理1.3知,滯后型測度泛函微分方程(2)與廣義常微分方程(7)在一定條件下等價,故它們的解均為有界變差函數且可以相互表示.以下證明滯后型測度泛函微分方程(2)的平凡解y≡0為變差穩定的.由假設V(y(t),t)對方程(2)的任何一解y:[t0,+∞)→Rn是不增函數,對任意的t∈[t0,+∞)有

以下證明在這種假設下滿足定義2.1的條件.

給定ε>0,令

y:[t0,t1]→Rn, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續.由于V滿足引理1.7的(12)式,其中Φ≡0.由(13)、(21)和(22)式,對于任意的r∈[t0,t1]可得

因為

|V(y(t0),t0)-V(0,t0)|≤L‖y(t0)‖∞,

且Φ≡0,所以

‖y(t0)‖∞<δ(ε).

由(16)式得

由(23)式有

V(y(r),r)≤L‖y(t0)‖∞+Lδ(ε)≤

Lδ(ε)+Lδ(ε),

所以當r∈[t0,t1]時,有以下不等式成立

V(y(r),r)≤2Lδ(ε).

(24)

如果存在ξ∈[t0,t1],使得‖y(ξ)‖∞≥ε,根據(20)式有

這與(24)式矛盾,故對于所有的t∈[t0,t1]有‖y(t)‖∞<ε,滿足定義2.1,即滯后型測度泛函微分方程(2)的平凡解y≡0是變差穩定的.

定理2.2設V:O×[0,+∞)→R滿足定理2.1中的條件,如果對于滯后型測度泛函微分方程(2)的任何一個解y:[t0,t1]→O,當t∈[t0,t1]時有

-Φ(y(t))

(25)

成立,其中Φ:Rn→R為連續函數且Φ(0)=0.當y≠0時,Φ(y)>0,則滯后型測度泛函微分方程(2)的平凡解y≡0為變差漸近穩定的.

證明由(25)式知,V(y(t),t)對滯后型測度泛函微分方程(2)的任何一個解y:[t0,t1]→Rn是不增函數.由定理2.1可知,滯后型測度泛函微分方程(2)的平凡解y≡0是變差穩定的,由定義2.3可知以下只需證明滯后型測度泛函微分方程(2)的平凡解y≡0是變差吸引的.

由定理2.1,滯后型測度泛函微分方程(2)的平凡解是變差穩定的,存在一個δ0>0,對任意的

y:[t0,t1]→Rn, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,使得‖y(t0)‖∞<δ0,且有

則對任意的t∈[t0,t1],有‖y(t)‖∞<δ0.對任意的ε>0,由滯后型測度泛函微分方程(2)的平凡解y≡0是變差穩定的可知,存在δ(ε)>0,使得對于每一個

y:[t2,t3]→Rn, 0≤t2

是區間[t2,t3]上的有界變差函數,并且在(t2,t3]上左連續,使得

‖y(t0)‖∞<δ(ε)

(26)

和

則對于t∈[t2,t3]有

‖y(t)‖∞<ε.

(28)

定義

γ(ε)=min(δ0,δ(ε)),δ0>0,

其中

A=sup{-Φ(y);γ(ε)≤‖y‖∞<ε}=

-inf{Φ(y);γ(ε)≤‖y‖∞<ε}<0,

且假設

y:[t0,t1]→Rn, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,使得‖y(t0)‖∞<δ0,且有

假設T(ε)

下面證明存在一個t*∈[t0,t0+T(ε)],使得有‖y(t*)‖∞<γ(ε).

運用反證法.假設上述結論不成立,即對于任意的s∈[t0,t0+T(ε)]有

‖y(s)‖∞≥γ(ε).

由引理1.7得

因此

V(y(t0+T(ε)),t0+T(ε))≤

V(y(t0),t0)-Lδ0≤

L‖y(t0)‖∞-Lδ0

這與不等式

V(y(t0+T(ε),t0+T(ε))≥

b(‖y(t0+T(ε))‖∞)≥b(γ(ε))>0

矛盾,所以必然存在一個t*∈[t0,t0+T(ε)],使得

‖y(t*)‖∞<γ(ε).

對于t1=t*,t3=t1這種情況,考慮到γ(ε)的選取,由于(26)、(27)式成立,因而(28)式也滿足.因此對于t>t0+T(ε),有‖y(t)‖∞<ε.由于t*∈[t0,t0+T(ε)],則滯后型測度泛函微分方程(2)的平凡解y≡0是變差吸引的.由定義2.3知滯后型測度泛函微分方程(2)的平凡解y≡0是變差漸近穩定的.

接下來討論受到擾動后的滯后型測度泛函微分方程(3)的變差穩定性與變差漸近穩定性.

定理2.3設V:O×[0,+∞)→R,使得對于任意的y∈O?G*([t0-r,+∞),Rn),r>0,函數V(y,·):[0,+∞)→R在區間(0,+∞)上是左連續的,假設V(y,·)是正定的,即存在一個連續遞增實函數b:[0,+∞)→R,使得b(ρ)=0當且僅當ρ=0,對所有的(y,t)∈O×[0,+∞),任意的x∈O,常數L>0有:

V(y,t)≥b(‖y‖∞),

(29)

V(0,t)=0,

(30)

和

|V(x,t)-V(y,t)|≤L‖x-y‖∞.

(31)

如果函數V(y(t),t)對滯后型測度泛函微分方程(3)的任何一個解y(t)是不增函數,則方程(3)的平凡解y≡0是變差穩定的.

證明由引理1.4,驗證G∈F(Ω,h),Ω=O×[t0,+∞).根據假設存在常數M、N、K,對于任意的y,z∈O.條件(H1)和(H4)暗示了在G的定義下積分存在,給定y∈O,若0≤t0

F(y,s2)(?)-F(y,s1)(?)=

P(s2)(?)-P(s1)(?)=

則由條件(H2)和(H5)有

‖F(y,s2)(?)-F(y,s1)(?)‖∞=

h1(s2)-h1(s1),

‖P(s2)(?)-P(s1)(?)‖∞=

h2(s2)-h2(s1),

即

‖G(y,s2)(?)-G(y,s1)(?)‖∞≤h1(s2)-

h1(s1)+h2(s2)-h2(s1)≤h(s2)-h(s1).

由條件(H3)有

‖G(y,s2)(?)-G(y,s1)(?)-

G(z,s2)(?)+G(z,s1)(?)‖∞=

‖y-z‖∞[h(s2)-h(s1)].

存在.因此,G∈F(Ω,h),其中h:[t0,+∞)→R為左連續不減函數,h1(t)、h2(t)由(11)式給出且

h(t)=h1(t)+h2(t).

由引理1.6知,滯后型測度泛函微分方程(3)與廣義常微分方程(10)在一定條件下等價,故它們的解均為有界變差函數且可以相互表示,以下證明滯后型測度泛函微分方程(3)的平凡解y≡0為變差穩定的.由假設V(y(t),t)對方程(3)的任何一解y:[t0,+∞)→Rn是不增函數,對任意的t∈[t0,+∞)有

以下證明在這種假設下滿足定義2.4的條件.

給定ε>0,令

y:[t0,t1]→Rn, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續.由于V滿足引理1.8的(14)式,其中Φ≡0.由(15)、(30)和(31)式,對于任意的r∈[t0,t1],可得

(32)

因為

|V(y(t0),t0)-V(0,t0)|≤L‖y(t0)‖∞,

且Φ≡0,所以

‖y(t0)‖∞<δ(ε).

由(18)式得

由(32)式有

V(y(r),r)≤L‖y(t0)‖∞+

Lδ(ε)≤Lδ(ε)+Lδ(ε),

所以當r∈[t0,t1]時,有以下不等式成立

V(y(r),r)≤2Lδ(ε).

(33)

如果存在ξ∈[t0,t1],使得

‖y(ξ)‖∞≥ε,

根據(29)式有

V(y(ξ),ξ)≥b(‖y(ξ)‖∞)≥

這與(33)式矛盾,故對于所有的t∈[t0,t1]有

‖y(t)‖∞<ε

滿足定義2.4,即滯后型測度泛函微分方程(3)的平凡解y≡0是變差穩定的.

定理2.4設V:O×[0,+∞)→R滿足定理2.3中的條件,如果對于滯后型測度泛函微分方程(3)的任何一個解y:[t0,t1]→Rn,當t∈[t0,t1]時有

-Φ(y(t))

(34)

成立,其中Φ:Rn→R為連續函數且Φ(0)=0.當y≠0時,Φ(y)>0,則滯后型測度泛函微分方程(3)的平凡解y≡0為變差漸近穩定的.

證明由(34)式知,V(y(t),t)對滯后型測度泛函微分方程(3)的任何一個解y:[t0,t1]→Rn是不增函數.由定理2.3可知,滯后型測度泛函微分方程(3)的平凡解y≡0是變差穩定的,由定義2.6可知以下只需證明滯后型測度泛函微分方程(3)的平凡解y≡0是變差吸引的.

由定理2.3,滯后型測度泛函微分方程(3)的平凡解是變差穩定的,存在一個δ0>0,對任意的

y:[t0,t1]→Rn, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,使得‖y(t0)‖∞<δ0,且有

則對任意的t∈[t0,t1],有‖y(t)‖∞<δ0.對任意的ε>0,由滯后型測度泛函微分方程(3)的平凡解y≡0是變差穩定的可知,存在δ(ε)>0,使得對于每一個

y:[t2,t3]→Rn, 0≤t2

是區間[t2,t3]上的有界變差函數,并且在(t2,t3]上左連續,使得

‖y(t0)‖∞<δ(ε)

(35)

和

(36)

則對于t∈[t2,t3]有

‖y(t)‖∞<ε.

(37)

令

γ(ε)=min(δ0,δ(ε)),

其中

A=sup{-Φ(y);γ(ε)≤‖y‖∞<ε}=

-inf{Φ(y);γ(ε)≤‖y‖∞<ε}<0,

且假設

y:[t0,t1]→Rn, 0≤t0

是區間[t0,t1]上的有界變差函數,并且在(t0,t1]上左連續,使得‖y(t0)‖∞<δ0,且有

(38)

假設T(ε)

以下證明存在一個t*∈[t0,t0+T(ε)],使得‖y(t*)‖∞<γ(ε).

運用反證法.假設上述結論不成立,即對于任意的s∈[t0,t0+T(ε)],有‖y(s)‖∞≥γ(ε).由引理1.7得

因此

V(y(t0+T(ε)),t0+T(ε))≤

V(y(t0),t0)-Lδ0≤

L‖y(t0)‖∞-Lδ0

這與不等式

V(y(t0+T(ε),t0+T(ε))≥

b(‖y(t0+T(ε))‖∞)≥b(γ(ε))>0

矛盾,所以必然存在一個t*∈[t0,t0+T(ε)],使得

‖y(t*)‖∞<γ(ε).

對于t1=t*,t3=t1這種情況,考慮到γ(ε)的選取,由于(35)和(36)式成立,因而(37)式也滿足.對于t>t0+T(ε),有‖y(t)‖∞<ε.由于t*∈[t0,t0+T(ε)],則滯后型測度泛函微分方程(3)的平凡解y≡0是變差吸引的.由定義2.6知滯后型測度泛函微分方程(3)的平凡解y≡0是變差漸近穩定的.