福州市中心城區交通擁堵程度識別研究

■趙銀柱 謝幸林 涂錦程 李承洲 王 鋒

(福州大學土木工程學院，福州 350116)

1 緒論

近年來，城市化水平快速提高、機動車保有量爆炸式增長，道路基礎設施無法滿足出行需求，城市交通擁堵越發嚴重。而城市的中心城區作為城市的政治文化中心和重要經濟功能集中體現的地區[1]，是交通流最為密集復雜的區域，它所面臨的交通擁堵問題也更為嚴峻棘手。通過大量新建道路基礎設施以及擴大原有道路車道數等手段，將會加劇機動車的增長，使交通流量持續上升，惡化交通出現擁堵。因此準確識別中心城區擁堵程度，對交通管理、交通疏導、提高道路通行能力具有重要的意義。

Hawas等[2]以模糊性數學理論為基礎，通過計算聚類隸屬函數來監測城市道路交通事件，可行性高且緩堵作用顯著。Bauza等[3]基于對車輛聯網、車輛感知范圍等研究，借助模糊分離器分析描述路段交通擁堵程度。Kong等[4]基于卡爾曼濾波理論，對道路檢測器與車輛GPS檢測器的原始數據進行預處理，通過GIS系統匹配速度與流量以識別交通狀態。黎符忠[5]建立了城市道路交通擁堵評價體系，包含交叉口、路段、區域指標，結合信息熵權值法與灰色理論，構造灰色關聯度評價模型，方案實施效果良好。劉志剛、金升[6]運用博棄論理論分析城市擁堵問題的產生原因，指出擁堵根源是“囚徒困境”，以及總結了四種城市擁堵解決對策。龍建成[7]構建動態的路網交通流傳播模型，研究交叉口的緊急交通流的傳播，構建了交叉口交通模型以及動態隨機路徑選擇模型。

本文在數據調查分析的基礎上，以模糊數學為基礎、隸屬函數為工具，建立模糊綜合評判模型，對中心城區擁堵狀態進行識別，為交通擁堵管理提供依據。

2 中心城區的相關問題

2.1 中心城區的界定

中心城區是所在行政區域城鎮體系中處于主導地位的城市建成區范圍，是具有城市政治、經濟、文化、社會引導功能的集中承載地區[1]。2017年11月3日通過的《福州中心城區空間發展規劃》，福州中心城區總面積約2881km2，范圍為：福州市轄五區，長樂全域，閩侯縣9個鄉鎮街道，以及連江縣琯頭鎮[8]，論文研究范圍為主城中心區。

2.2 中心城區道路系統

中心城區道路系統是城市道路系統的重要組成部分，可以依照《城市道路交通規劃設計規范》，將其劃分為：快速路，主干路，次干路，支路。

以上四個等級城市道路的可達性與機動性關系見圖2。

交叉口是道路與道路的相交節點，將各條道路相聯結形成路網。交叉口是道路通行能力的瓶頸，制約道路甚至路網的服務水平。結合本文的研究內容，將研究對象定位為中心城區的主干路。

3 中心城區交通擁堵的模糊綜合評判模型

3.1 評價指標集的確定

結合評價指標選取原則，確定該模型評價指標集為：U={u1，u2，u3，u4}={D，S，Z，T}={路段擁堵延時指數，路段飽和度，交叉口飽和度，交叉口延誤時間}，中心城區交通擁堵度的評價指標體系如圖3所示。

圖1 福州中心城區空間結構示意圖

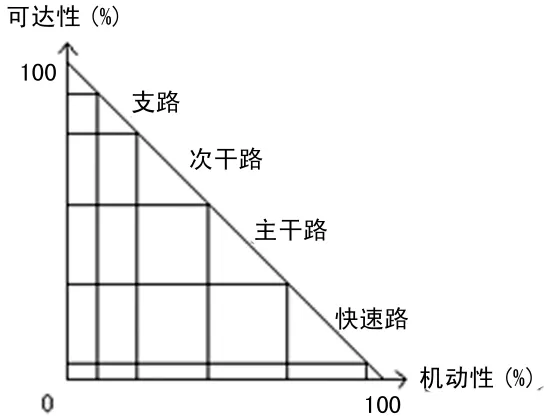
圖2 不同等級道路的機動性與可達性

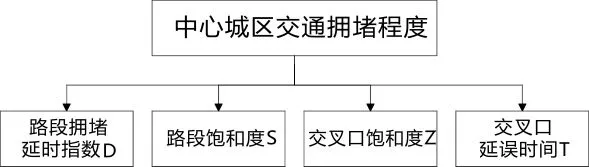
圖3 中心城區交通擁堵評價指標體系

3.2 評判標準的建立

根據交通擁堵等級評判的標準，將中心城區交通擁堵程度劃分為暢通、緩行、擁堵、堵塞，即確定該模型的評判標準集為：V={v1，v2，v3，v4}={暢通，緩行，擁堵，堵塞}。

3.3 隸屬函數的構造

隸屬函數是基于模糊集合而發展的，模糊集合運用隸屬函數rA(x)來描述元素對模糊集合的隸屬程度，隸屬程度的取值是[0，1]。隸屬函數可以表示屬于的概念，即rA(x)=1；也可以表示不屬于的概念，即rA(x)=0；還可以表示模糊臨界的概念，即rA(x)∈(0，1)[9]。隸屬函數的數學表達公式如下：

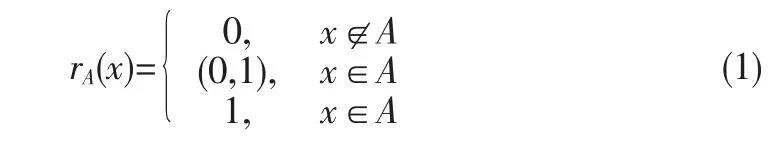
在模糊性數學理論中，常用的隸屬函數有梯形函數、三角形函數、S型函數和正態函數等。由于梯形隸屬函數具有容易理解、計算簡單、分辨率高、性質穩定等優點，故選取梯形隸屬函數。

3.3.1 梯形隸屬函數的構造方法

隸屬函數的精確度取決于模糊分級，即精確劃分屬于區間、模糊臨界、不屬于區間。如圖4的梯形隸屬函數，Fk的屬于區間為，模糊臨界為與，不屬于區間為與

3.3.2 中心城區交通擁堵程度的模糊分級

借鑒目前正在使用的交通擁堵量化標準，運用模糊分級的方法，對中心城區交通擁堵程度做出如下的量化分級，如表1所示。

圖4 梯形隸屬函數的一般形式

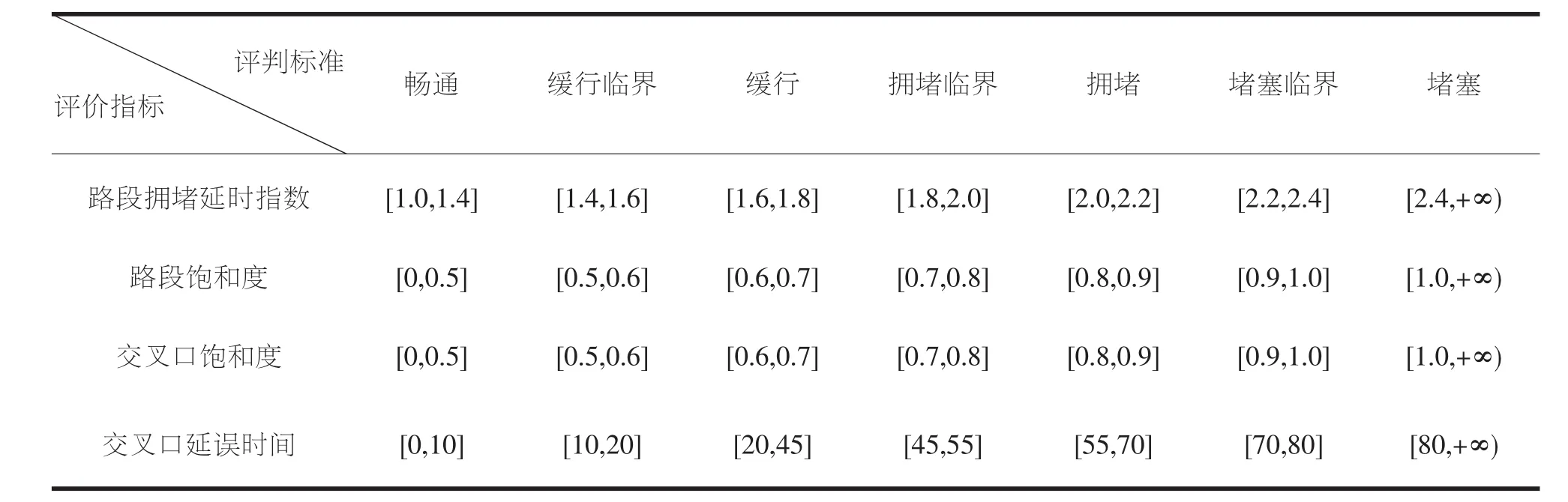
表1 中心城區交通擁堵程度的模糊分級

3.3.3 路段擁堵延時指數的隸屬函數

由表1可知，路段擁堵延時指數為D∈[1.0，1.4]時呈現暢通狀態，D∈[1.6，1.8]時呈現緩行狀態，D∈[2.0，2.2]時呈現擁堵狀態，D∈[2.4，+∞]時呈現堵塞狀態。其余區間為相鄰交通狀態的模糊臨界，呈現“亦此亦彼”的交通狀態。路段擁堵延時指數的隸屬函數如公式(2)如所：

因此路段擁堵延時指數D的模糊關系向量R1=(r11，r12，r13，r14)，其中每個r1j分別代表路段擁堵延時指數 D對暢通、緩行、擁堵、堵塞的隸屬程度。

3.3.4 路段飽和度的隸屬函數

路段飽和度的隸屬函數如公式(3)所示，r21、r22、r23、r24用以計算路段飽和度S對暢通、緩行、擁堵、堵塞等狀態的隸屬程度。

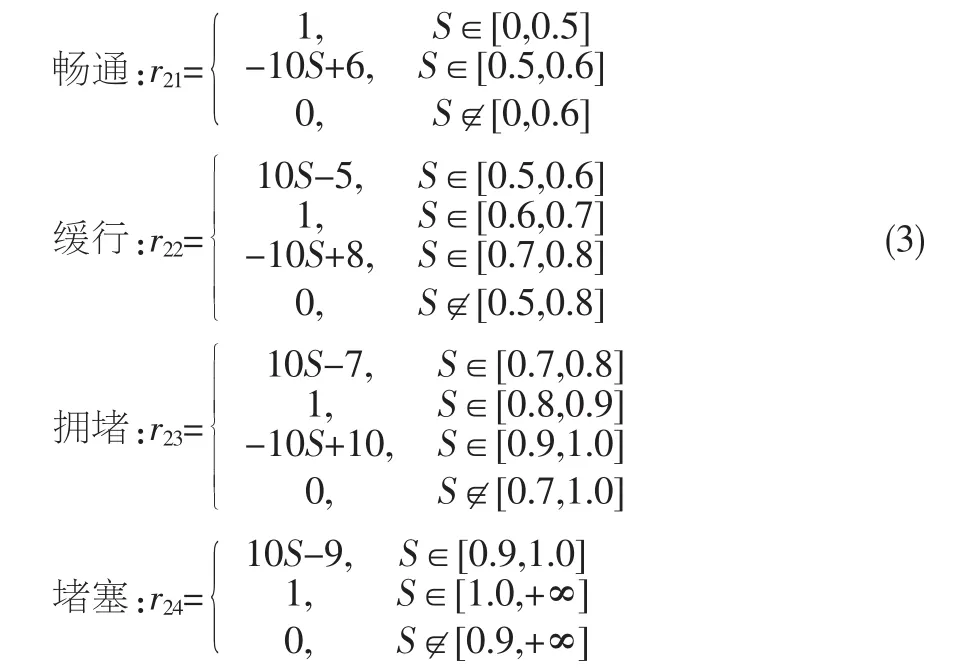
3.3.5 交叉口飽和度的隸屬函數

由表1可知，交叉口飽和度Z與路段飽和度S的量化分級取相同數值，所以除了自變量的定義與取值不同之外，交叉口飽和度Z的隸屬函數圖象、公式與路段飽和度S基本一致，交叉口飽和度的隸屬公式如式(4)所示。

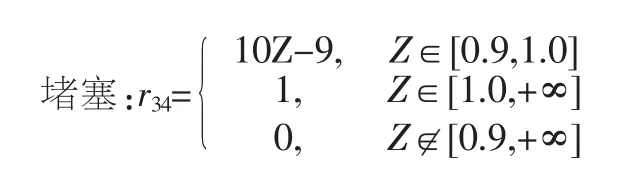
故，交叉口飽和度Z的模糊關系向量R3=(r31，r32，r33，r34)，其中每個r3j依次代表交叉口飽和度Z對暢通、緩行、擁堵、堵塞的隸屬程度。

3.3.6 交叉口延誤時間的隸屬函數

交叉口延誤時間如公式(5)所示。

故交叉口延誤時間T的模糊關系向量R4=(r41，r42，r43，r44)，其中每個r4j依次代表交叉口延誤時間T對暢通、緩行、擁堵、堵塞的隸屬程度。

3.4 指標權重的確定

在考慮用于評價中心城區交通擁堵程度的指標時，交叉口飽和度最為重要(34%)，繼而依次為交叉口延誤時間(32%)、路段飽和度(18%)、路段擁堵延時指數(16%)。 通過判斷矩陣一致性檢驗，可以確定評價中心城區交通擁堵程度的指標權重集為：W={w1，w2，w3，w4}={w路段擁堵延時指數，w路段飽和度，w交叉口飽和度，w交叉口延誤時間}={0.16，0.18，0.34，0.32}。

3.5 模糊合成值的計算方法

模糊合成值的計算模型為 ，式中δ稱為廣義模糊算子。在數學理論中存在無窮多種廣義模糊算子，實際運用中常見有以下4種。

表2 廣義模糊算子

故，選擇M(●，⊕)進行模糊合成值的計算，它綜合考慮主次因素且得到的模糊合成值B具有歸一性。

3.6 模糊綜合評判結果的確定方法

兩種確定模糊綜合評判結果的方法見表3，本文選最大隸屬度法。

表3 模糊綜合評判結果的確定方法

4 模型的運用

4.1 數據調查

本文選取福州鼓樓區位于勞動大廈附近的一條城市主干路——古田路作為研究對象，路段(含交叉口)長度為0.784km。調查時段取工作日晚高峰，每15min統計一次交通數據。在調查路段的起終點各安排調查人員，讀取車輛經過路段的時間以及記錄車牌的后三位。數據整理階段將觀測數據按照相同車牌號進行匹配，車輛通過路段首尾時間得到行駛時間相減，結合路段長度，多組數據取平均值得到行程車速。以停車線為觀測斷面分車種分流向進行交叉口交通量調查。通過記錄在停車線后面的車輛數及經過停車線的停駛數和不停駛數進行交叉口延誤時間調查。統計結果如表4所示：

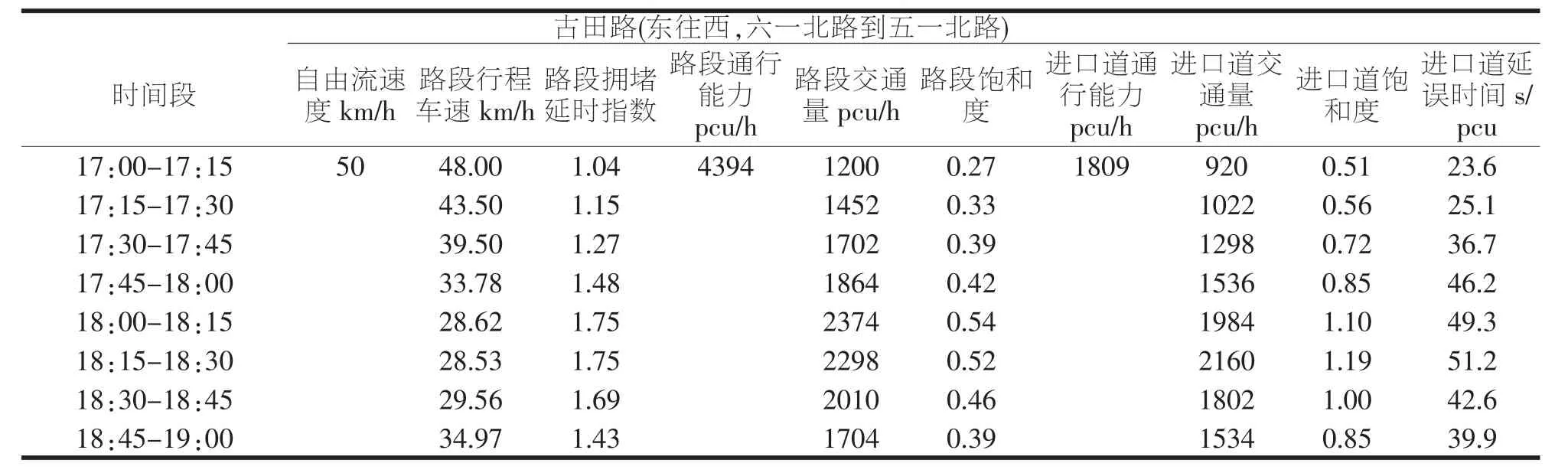
表4 交通數據匯總表

4.2 模型分析

將統計數據帶入模糊綜合評判模型中計算，計算過程如下：

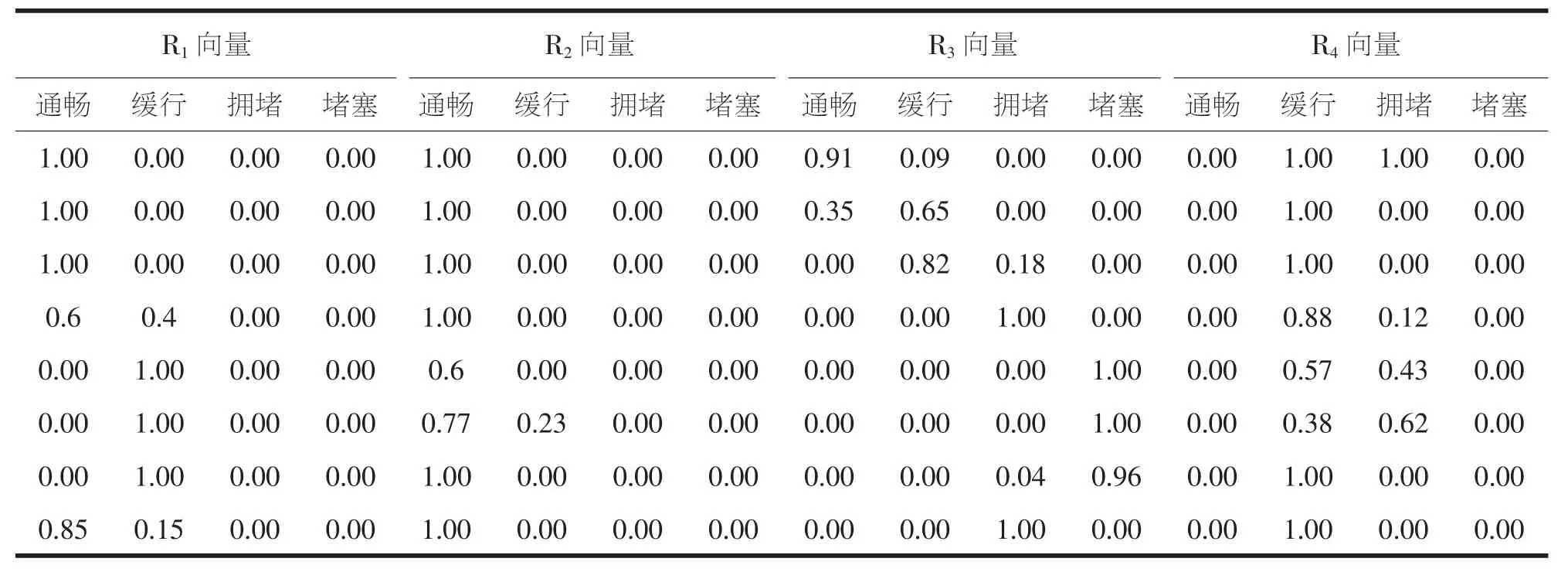
表5 計算模糊合成值

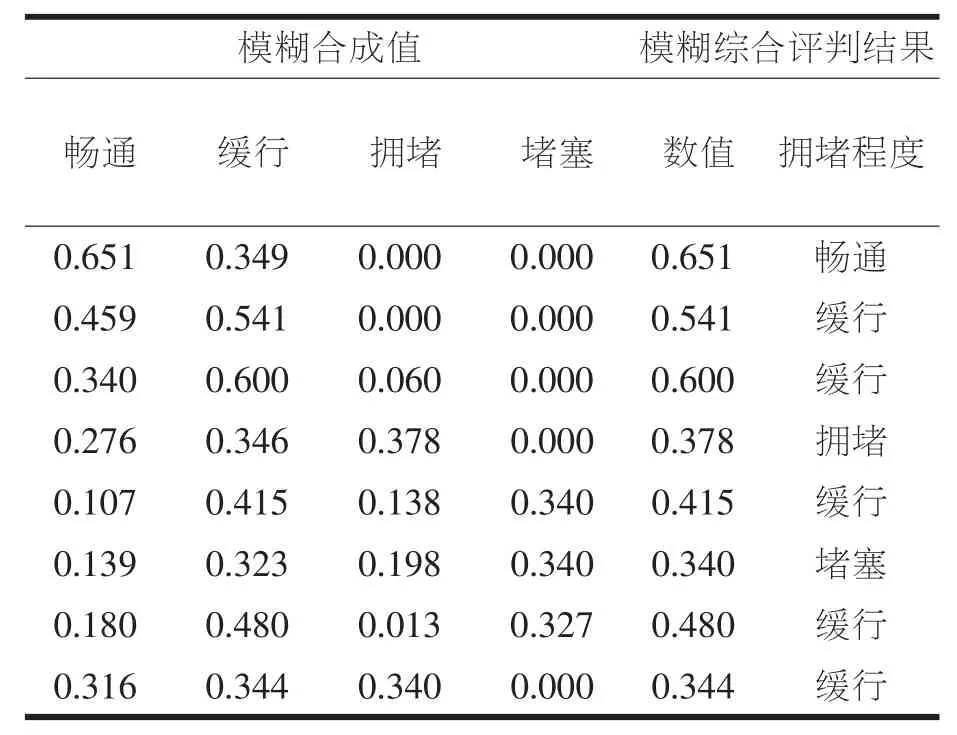
表6 模糊綜合評判結果

4.3 結果對比

最終用模糊綜合評判模型統計分析的交通擁堵情況下，將其與福州交警app公布的實時路段及交叉口交通狀態進行對比，評判結果基本一致，故該模型具有一定可行性．

表7 模型計算結果

4.4 模型運用

用該模型計算鼓樓區其他路段的擁堵程度，見下表8：

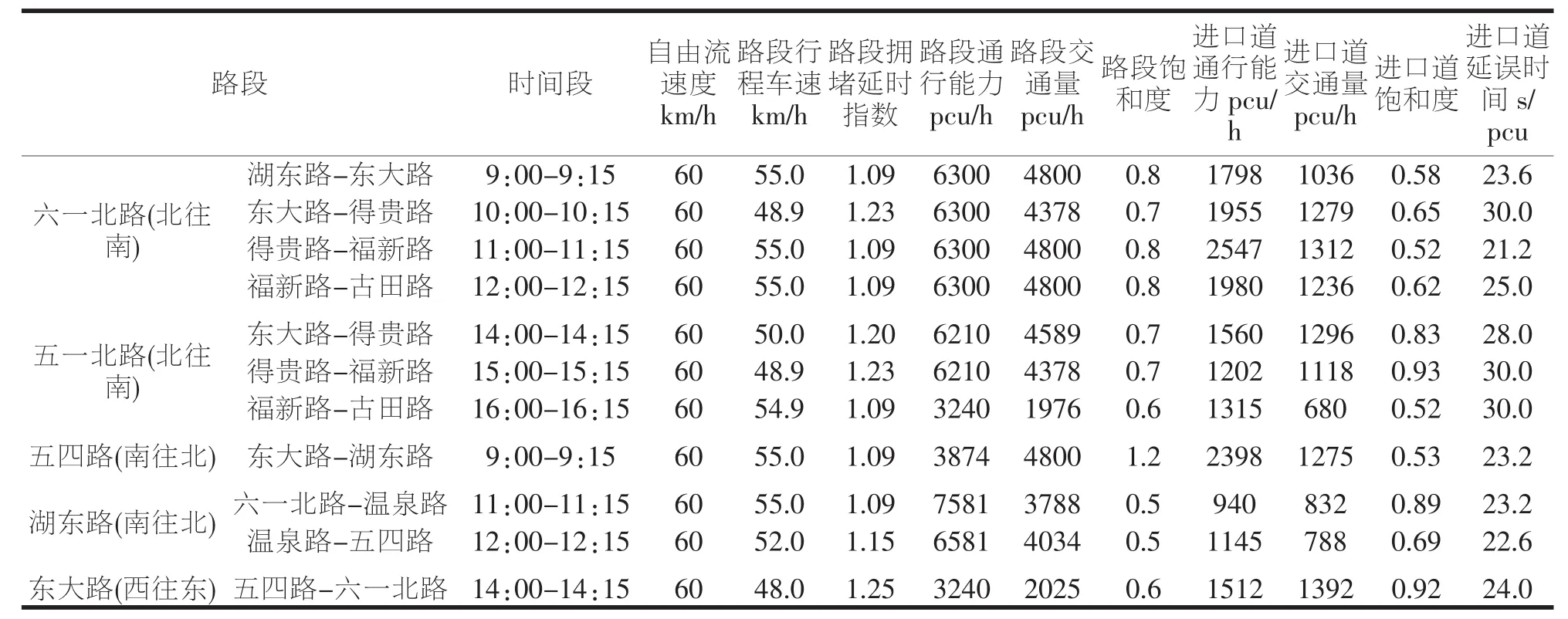
表8 計算模糊合成值

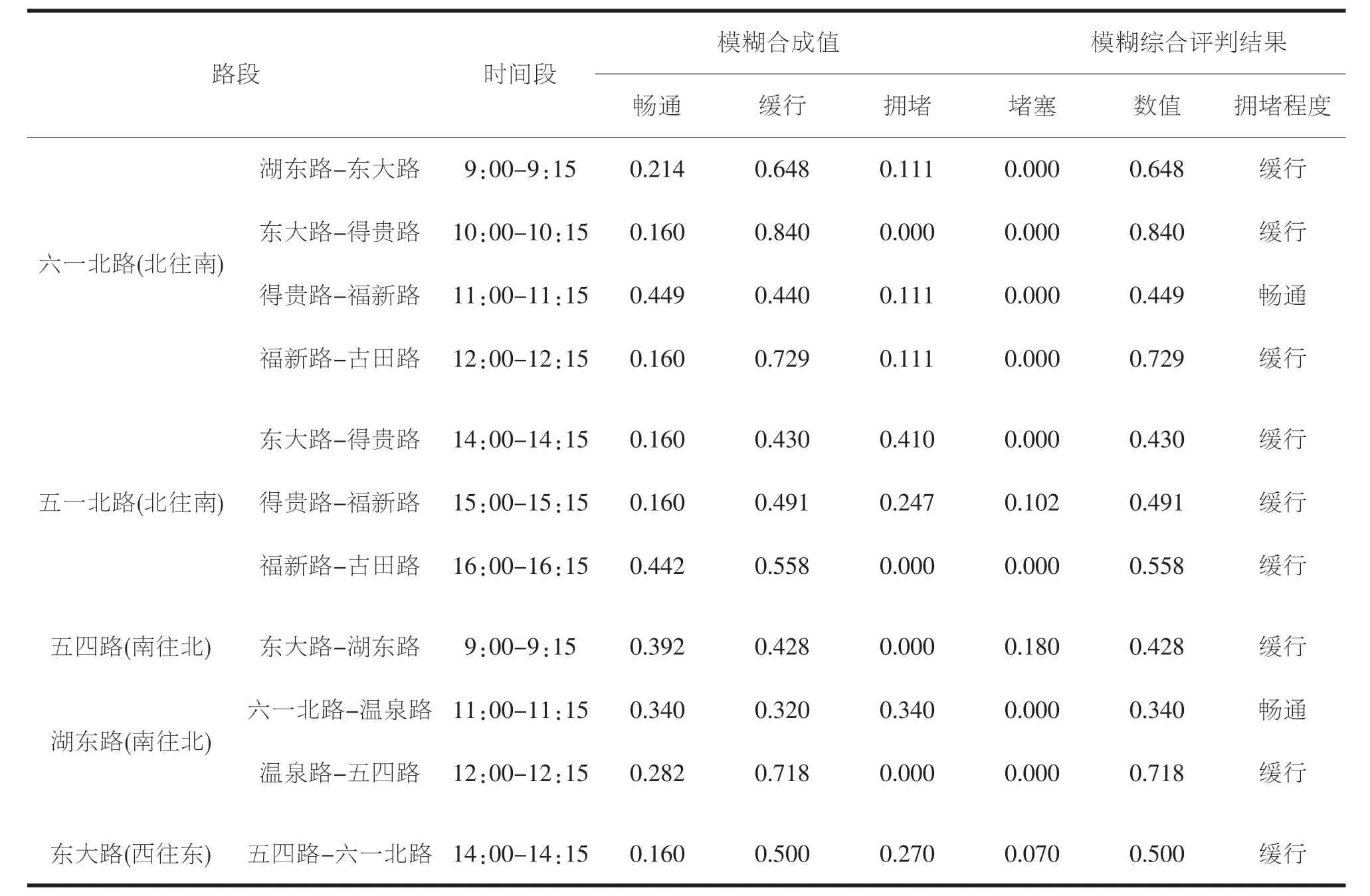
表9 模糊綜合評判結果

5 結語

中心城區交通暢通的作用和重要性日益凸顯，其擁堵程度識別的研究存在很大的價值，通過模糊綜合評判法的模糊綜合評判模型對主城中心區交通擁堵等級進行評價，主城中心區幾條主干道在工作日晚高峰基本處于緩行和擁堵的狀態。