變化環境下考慮線型不確定性的水文設計值估計
張 潔,梁忠民,胡義明,王 軍,李彬權
(河海大學水文水資源學院,南京 210098)
洪水資料的一致性是現行水文頻率分析計算的基本前提[1]。近年來,人類活動和氣候變化使得洪水形成的下墊面和氣候條件發生了重大改變,水文極值系列不再具有一致性,那么一致性條件下的水文頻率分析方法在變化環境下也就不再適用[2-7]。因此,變化環境下非一致性水文頻率分析方法的研究成為廣大學者的研究重點,其中,基于變參數概率分布模型途徑的非一致性水文頻率分析是目前研究最為廣泛的方法之一[8-10]。其通過分析不同變參數概率分布模型的擬合效果,選取擬合最優的模型作為最終使用模型。在此基礎上,采用期望等待時間法、期望發生次數法、設計壽命水平法[9]或等可靠度法[10]推求變化環境下特定重現期對應的非一致性水文設計值。水文設計值推求的可靠性受諸多因素影響,如模型類型、參數估計等。胡義明等研究了變參數概率分布函數模型中參數估計不確定性、模型輸入不確定性以及2者耦合對水文設計值估計的影響[9]。變化環境下非平穩的水文極值系列理論上的變參數概率分布模型無法得知,這使得依據擬合最優原則獲得的最優模型也未必能精準地代表非平穩極值系列的概率分布特征,導致依據單一最優擬合模型計算的結果不可避免地存在不確定性。
為此,本文選取赤池信息準則(AIC)評估了多個變參數概率分布模型的擬合效果,提出將擬合效果較好的若干種變參數概率分布函數模型進行綜合,以減小模型選擇對水文設計值產生的不確定性影響,增強水文頻率分析計算得到的水文設計值的可靠性。
1 方法原理
1.1 “等可靠度”法基本原理
下面介紹“等可靠度”法。假定工程設計壽命期為L,且n年的歷史洪峰資料x1,x2,…,xn存在減少趨勢;采用“等可靠度”法推求重現期為T的設計洪水的基本流程可表述如下[9]。
首先采用分布參數隨時間等協變量的變化而變化的變參數PE3概率分布函數描述該洪峰系列。假定尺度參數β和形狀參數γ為不隨時間變化的常數,而位置參數μ隨時間線性變化,即:
μ(t)=μ0+μ1t
(1)
β=β0
(2)
γ=γ0
(3)
此時,變參數的PE3概率密度函數可表示為:
(4)
變參數PE3概率分布函數為Ft[μ(t),β,γ],t=1,2,…,n,其中的參數μ0、μ1、β和γ可由n年的歷史洪峰數據x1,x2,…,xn估計得到,進而推求工程壽命期內(n+1~n+L)逐年的變參數PE3概率分布函數Ft[μ(t),β,γ],t=n+1,n+2,…,n+L。則變化環境下水文設計值XT,NS的水文可靠度為:
(5)
(6)
(7)
根據“等可靠度”法,變化環境的非一致性條件下不再具有重現期的概念,但非一致性條件下計算的水文設計值所具有的可靠度至少應該達到一致性條件下計算的設計值的可靠度。令:
RNS=RS
(8)
求解式(8),即可得到變化環境下非一致性條件的水文設計值XT,NS。
1.2 考慮模型選擇不確定性的設計值計算
采用變參數概率分布模型進行變化環境下非一致性水文頻率分析時,由于人類活動和氣候變化對水文極值系列分布規律產生了很大影響,因此將分布函數中的參數設定為隨時間等協變量而改變的變量,而不再采用常數。然而,概率分布中參數隨協變量變化的準確關系是未知的,現階段擬合效果最好的模型并不能保證在未來也始終優于其他模型,隨著時間的外延,水文設計值估計的可靠性越來越低,而不確定性隨之增大。為降低模型選擇導致的不確定性,增強水文頻率分析計算結果的可靠性,可綜合考慮多個擬合效果較好的變參數概率分布模型,其中,各模型的權重可由其擬合程度確定。下面闡述推求設計重現期為T,工程設計壽命為L的水文設計值的具體過程。
(1)以不同的概率分布函數(如PE3概率分布函數、廣義極值分布函數等)為基礎,構建不同的變參數概率分布函數模型來擬合變化環境下非平穩的水文極值系列。假定概率分布函數中位置參數、尺度參數、形狀參數等參數隨時間這一協變量的變化而變化,采用AIC指標評估各模型擬合效果,并根據擬合效果選出擬合效果最優的前m個模型,記為Mi,i=1,2,…,m。
(2)基于“等可靠度”法計算步驟(1)中第i個模型Mi對應的水文設計值X(Mi),i=1,2,…,m:
(9)
(3)采用AIC指標對擬合效果進行評估。AIC值越小的模型擬合效果越好,其所占權重也應該越大。根據評估結果,計算模型Mi的權重wi,i=1,2,…,m;
(10)
式中:AICi為第i個模型Mi的AIC值。
(4)將m個模型計算的水文設計值X(Mi)加權平均,獲得綜合水文設計值X,進而降低模型選擇的不確定性影響。即:
(11)
值得注意的是,公式(10)僅適用于經AIC評估后2個或2個以上模型的AIC值接近且明顯小于其他模型的情況。權重的計算僅限于擬合效果較好的模型,而不能應用于建立的全部模型。當某個模型的AIC值明顯小于其他模型時,可直接采用此最優模型進行水文頻率分析計算。AIC值作為評估模型擬合效果的指標,具有對各模型篩選比較的功能,AIC值明顯較高的模型擬合效果差,應該及時去除,否則不能發揮AIC指標的功能,將大大增加水文設計值的誤差。公式(10)的作用是在AIC指標排除較差模型的基礎上,將篩選得到的優秀模型進行綜合,以進一步增強水文頻率分析計算的可靠性。
2 實例研究
本文研究對象為黃龍灘站1956-2014年共59 a的7 d洪量歷史觀測資料,黃龍灘站所在流域的位置、水系和水庫分布等情況[4]見圖1。圖2為7 d洪量系列的時間序列圖。由圖2可知,7 d洪量系列明顯地隨時間而減小。
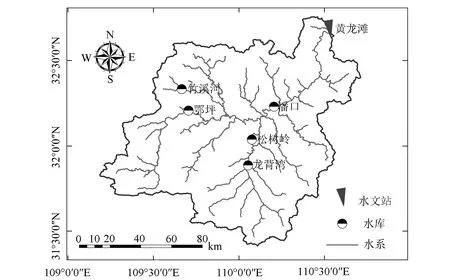
圖1 黃龍灘所在流域基本情況Fig.1 Basic information map of Huanglongtan river basin
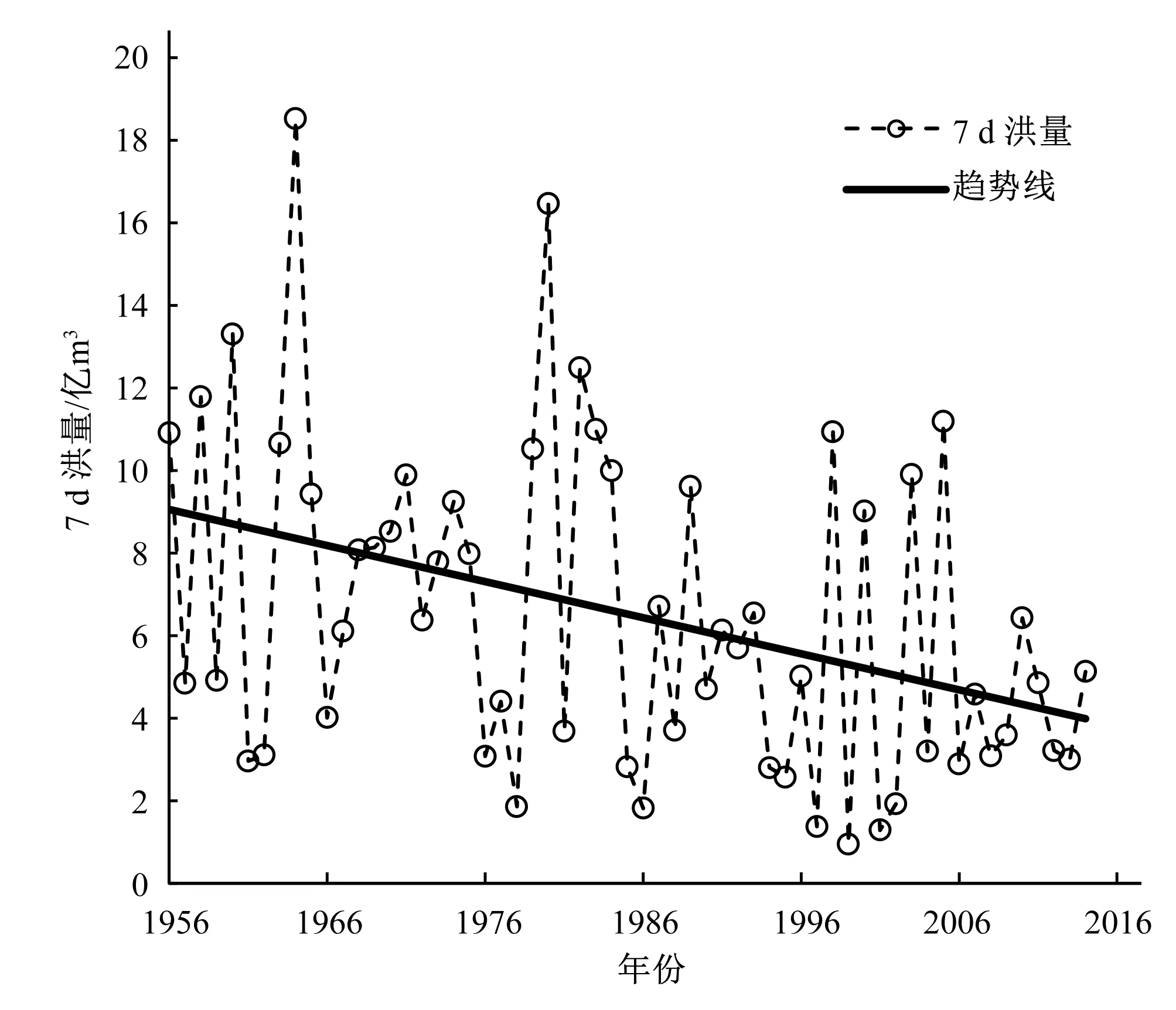
圖2 7 d洪量時間序列Fig.2 Time series of 7 day flood volume
選定時間作為協變量,通過假設PE3和GEV分布函數的位置參數或尺度參數并非常數而是隨協變量變化的變量,建立下面4個不同的變參數概率分布模型。每個模型中參數與協變量的關系如下。
(1)模型1:PE3分布函數中的尺度參數β和形狀參數γ為不隨時間變化的常數,而位置參數μ是隨時間線性變化的變量,記為PE3-Loc,即:
μ(t)=μ0+μ1t,β(t)=β0,γ(t)=γ0
(12)
(2)模型2:PE3分布函數中的形狀參數γ為不隨時間變化的常數,而位置參數μ和尺度參數β是隨時間線性變化的變量,記為PE3-Loc-Scl,即:
μ(t)=μ0+μ1t,β(t)=exp(β0+β1t),γ(t)=γ0
(13)
(3)模型3:GEV分布函數中的尺度參數α和形狀參數γ為不隨時間變化的常數,而位置參數ξ是隨時間線性變化的變量,記為GEV-Loc,即:
ξ(t)=ξ0+ξ1t,α(t)=α0,γ(t)=γ0
(14)
(4)模型4:GEV分布函數中的形狀參數γ為不隨時間變化的常數,而位置參數ξ和尺度參數α是隨時間線性變化的變量,記為GEV-Loc-Scl,即:
ξ(t)=ξ0+ξ1t,α(t)=exp(α0+α1t),γ(t)=γ0
(15)
采用貝葉斯方法對模型參數進行估計,模型的估計參數為最大后驗概率值對應的參數。平行運行5條鏈,在經過1 000次采樣后,各個模型的采樣樣本已收斂。每條鏈上除去用于預熱的前面900個樣本后余下100個參數,總共余下500個參數組,而參數的最大后驗估計就是得到最大參數后驗密度值的參數。計算各個模型的AIC值,以此作為指標評估各模型的擬合效果,見表1。

表1 不同模型擬合的AIC指標值Tab.1 AIC for assessing the model performance
由表1可知,AIC指標值最小的模型是模型2即PE3-Loc-Scl模型,由此得到此模型具有最好的擬合效果。模型4即GEV-Loc-Scl次之,且2模型的AIC值較為接近。直接采用PE3-Loc-Scl模型進行7 d洪量設計值計算可能存在誤差,故綜合考慮PE3-Loc-Scl和GEV-Loc-Scl 2種模型,以降低模型選擇對水文設計值產生的不確定性影響,增強水文頻率分析計算結果的可靠性。
分別將PE3-Loc-Scl和GEV-Loc-Scl的 AIC指標值的倒數占2種模型AIC指標值倒數之和的比重作為其權重,見表2。

表2 PE3-Loc-Scl和GEV-Loc-Scl的權重計算Tab.2 The weights of PE3-Loc-Scl and GEV-Loc-Scl
計算重現期為100 a時,PE3-Loc-Scl模型、GEV-Loc-Scl模型和綜合模型計算的7 d洪量設計值隨時間的變化趨勢,見圖3。

圖3 PE3-Loc-Scl模型、GEV-Loc-Scl模型和綜合模型100 d一遇7 d洪量設計值的時間變化規律Fig.3 The change with time of design values of one-hundred-year 7 day flood volume for the PE3-Loc-Scl model、the GEV-Loc-Scl model and the comprehensive model
根據圖3,PE3-Loc-Scl模型、GEV-Loc-Scl模型和綜合模型計算的重現期為100 a時的7 d洪量設計值均隨時間呈減少趨勢,與7 d洪量實測資料的趨勢相一致。PE3-Loc-Scl模型和GEV-Loc-Scl模型的100 a一遇7 d洪量設計值存在差異,2者加權平均后的綜合模型得到的綜合設計值可能具有更高的可靠度。在1956-2014年總共59 a的7 d洪量實測資料中,有0次超過綜合模型100 a一遇7 d洪量設計值,表明綜合模型的擬合效果較好。
基于PE3-Loc-Scl模型、GEV-Loc-Scl模型和綜合模型,采用“等可靠度”法計算設計標準為100 a一遇和20 a一遇時,40、60、80、100 a的工程設計壽命對應的7 d洪量設計值,結果見圖4。盡管PE3-Loc-Scl模型和GEV-Loc-Scl模型的擬合效果接近,但根據2者計算的7 d洪量設計值卻存在較大差異。由于無法知曉其理論分布,因此,2個模型都未必能精準地代表該洪量系列的概率分布特征,故對2個模型的計算結果進行加權綜合獲得綜合設計值,以盡可能地降低模型選取對設計值的影響。
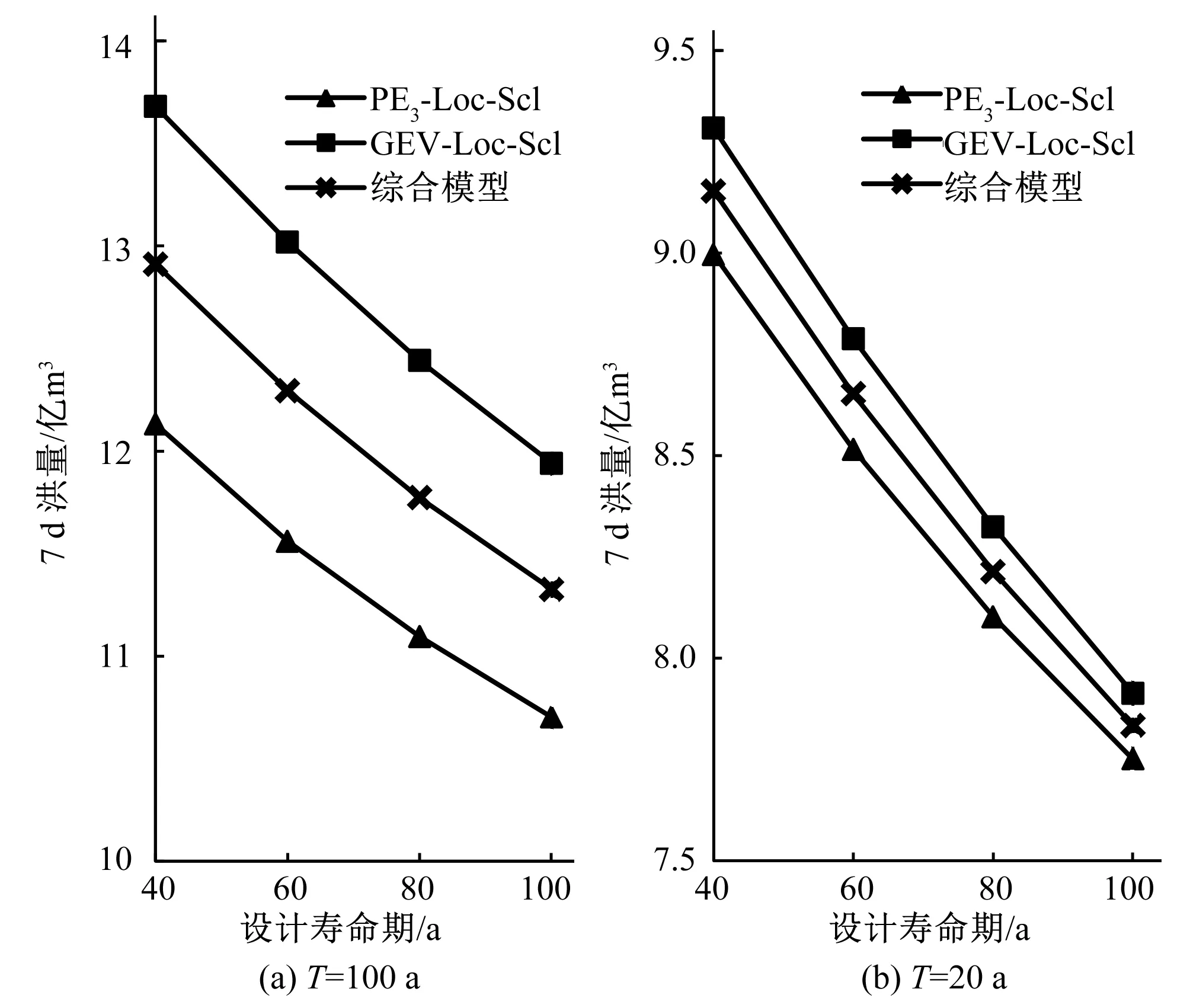
圖4 不同工程設計壽命期及重現期下3種模型推求的7 d洪量期望估計Fig.4 Design value for 7 day flood volume of three models with different return periods under the conditions of different design engineering life
3 結 論
(1)采用AIC指標評估多個模型對7 d洪量系列的擬合效果,并根據AIC評估結果計算較優模型的權重,綜合不同變參數概率分布模型的計算結果。
(2)較優模型具有相近的擬合效果,但推求的設計值卻表現出較大差異性。通過綜合多個較優模型的計算結果,一定程度上增強了計算結果的可靠性。
(3)當采用其他方法(如期望等待時間法等)推求非一致性條件下水文設計值時,同樣可以采用類似方法計算綜合水文設計值以減小模型選擇的不確定性。

