考慮基巖蠕變特性的重力壩深層抗滑穩定性分析

趙夢瑤，李同春,2，林潮寧

(1.河海大學水利水電學院，南京 210098；2. 河海大學水資源高效利用與工程安全國家工程研究中心，南京 210098)

0 引 言

當下我國水利工程事業面臨的一大緊迫問題就是地質條件優良的壩址開發殆盡，這導致越來越多的大壩將會被建在力學性質較差的基巖上。重力壩依靠自重保持穩定并抵擋水壓力，當重力壩壩基存在緩傾角軟弱夾層時，壩體將存在沿軟弱結構面滑動的可能，因而驗算重力壩的深層抗滑穩定性是非常必要的。目前強度折減法以其可以反映巖土體非線性本構關系、得到應力分布且不需要提前假定滑動面的位置和形狀的突出優點，得到了廣泛的應用。已經有許多學者證明了強度折減法在重力壩抗滑穩定性分析方面的可行性[1,2]，但是常規的彈塑性強度折減法在計算過程中僅考慮巖體材料的彈塑性力學性質，而忽略了巖石的長期變形特性。巖石均具有蠕變特性[3]，尤其是以泥巖、頁巖為代表的軟巖，在恒定的應力條件下，會產生較大的蠕變變形。以往重力壩選址均在較為堅固的巖質地基，巖石的蠕變特性并不明顯，因而可以將基巖視作彈塑性材料處理。但當重力壩壩基巖性軟弱時，巖體的蠕變特性無法忽視，即使荷載不變，壩基變形和應力也是不斷發生變化的，這將導致實際工程中重力壩的穩定性成為隨時間變化的量。鑒于此，本文以FLAC3D為平臺，利用考慮蠕變的強度折減法以及常規的彈塑性強度折減法計算重力壩的深層抗滑穩定性，比較分析軟弱基巖的蠕變特性給重力壩的深層抗滑穩定性帶來的影響，為建在軟弱基巖上的重力壩工程提供設計和監測參考。

1 考慮蠕變特性的重力壩深層抗滑穩定分析方法

強度折減法最早是1975年由Zienkiewicz在邊坡的穩定分析中首次提出的。該方法的計算思路是：在巖土體彈塑性有限元計算中分析，將抗剪強度參數c和tanφ除以一個系數f使之折減，再將得到的新參數c′和tanφ′代入數值模型進行計算，得到巖土體的位移變化及應力分布狀態。不斷增大折減系數f，直至巖土體發生失效破壞，此時對應的折減系數f即為該工程巖土體的抗滑穩定安全系數K。

目前已經有學者[4,5]采用考慮流變的強度折減法進行了邊坡穩定計算，證明了巖土體的流變特性對邊坡穩定有不利影響。本文提出考慮蠕變特性的重力壩深層抗滑穩定分析方法，即在強度折減法中對重力壩壩基巖體引入黏彈塑性蠕變本構模型，使得數值計算中的地基巖土體能夠體現其蠕變性質，而深層抗滑穩定安全系數仍采用折減其彈塑性抗剪強度參數的方式得到。

1.1 蠕變本構模型選取及參數確定

Burgers模型已被眾多學者用于擬合泥巖、砂巖、砂質泥巖等巖土體的蠕變試驗數據，結果表明，Burgers模型可以較好地反映巖體的初始蠕變和穩定蠕變階段[6-8]。本文選用FLAC3D中的Cvisc模型來模擬軟弱基巖的黏彈塑性，該模型由Burgers模型和Mohr-Coulomb模型串聯而成(見圖1)。圖1中σ為巖土體的應力；EM和EK為彈性模量和黏彈性模量；ηM和ηK分別為Maxwell黏性系數和Kelvin黏性系數；σt為巖土體材料的屈服強度；εM、εK和εP分別為Maxwell體的應變、Kelvin體的應變和塑性應變。

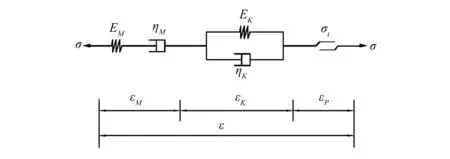
圖1 Cvisc蠕變模型示意Fig.1 Schematic diagram of Cvisc creep model

確定蠕變模型之后，根據巖石的蠕變試驗數據，利用巖體的瞬時變形可以確定彈性和彈塑性參數，然后利用穩定蠕變產生的變形確定黏彈性參數，最后用非穩定蠕變階段的變形求出黏塑性參數。考慮到如果巖體產生穩定蠕變或加速蠕變，則巖體在抗剪強度不折減的情況下也會產生隨時間不斷增長的變形，因此把麥克斯韋爾黏性系數ηM取為無窮大值，此時巖體將僅產生衰減蠕變，隨著時間推移，巖體的變形最終趨于穩定。

Cvisc從蠕變與應力偏量的關系分析， Cvisc蠕變模型在三維狀態下的表達式為：

(1)

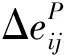
(2)

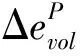
(3)

1.2 數值計算中重力壩失穩判據的選擇

在邊坡穩定分析中，對于強度折減法計算的失穩判據一般為：①數值計算不收斂；②形成從坡頂到坡腳全部貫通的塑性區；③在滑動帶上選取的關鍵點的位移值發生突變。由于當數值計算中考慮材料的蠕變變形時，在每個時間步內無法令節點不平衡力迭代減小為零，因而不能通過數值計算的不收斂來判斷壩體產生失穩。有學者提出[4]，利用FLAC3D中的Cvisc蠕變模型進行滑坡穩定性計算時，如果邊坡滑動帶上選取的關鍵點的位移無法在一段時間后達到穩定，則認為邊坡失穩。由于重力壩壩基兩側存在約束，當軟弱夾層傾角較緩且在壩址上下游附近均不出露時，地基破壞體現為整個區域的屈服，而不會像邊坡失穩一樣產生一條狹窄的貫通帶，地基剪切破壞帶上監測點的位移變化并不明顯。綜合考慮上述原因，本文用考慮蠕變的強度折減法計算重力壩穩定性時采用的失穩判據為：①壩頂特征點的位移在較長時間之后無法趨于穩定值；②壩基大面積屈服且貫通上下游。其中以前者為主要判斷依據，結合后者來綜合判斷壩體的穩定性。

2 算例分析

為分析基巖的蠕變特性對重力壩深層抗滑穩定安全性產生的影響，本文以圖2所示的重力壩計算模型為例，采用FLAC3D軟件先后進行常規的彈塑性強度折減法以及考慮蠕變的強度折減法計算。模型中基巖整體巖性較為軟弱，且帶有緩傾角軟弱夾層，取壩高為100 m，壩基影響范圍為400 m×200 m，縱向取10 m厚度。軟弱夾層傾角為3°，厚度0.3 m。

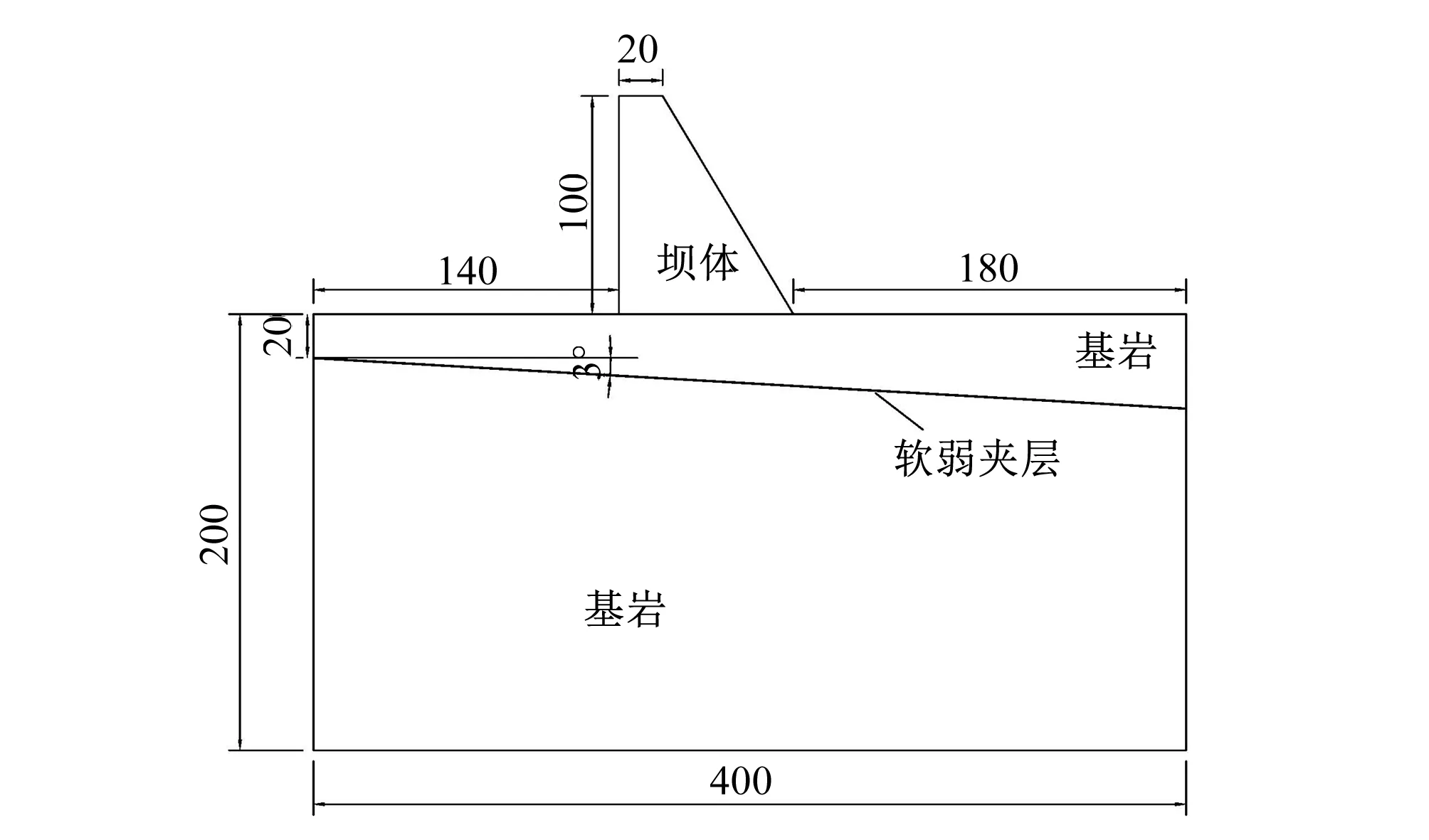
圖2 重力壩模型(單位：m)Fig.2 Gravity dam model

2.1 邊界條件及模型參數

結合實際的受力情況將地基底部完全固定，并對其上下游兩側施加法向約束。為簡化計算，算例僅考慮自重及水荷載，假定蓄水達到壩頂不計淤沙壓力及浪壓力等對重力壩深層滑動的影響。選取重力壩上游頂點作為監測位移的特征點，荷載施加及材料分布等見圖3。

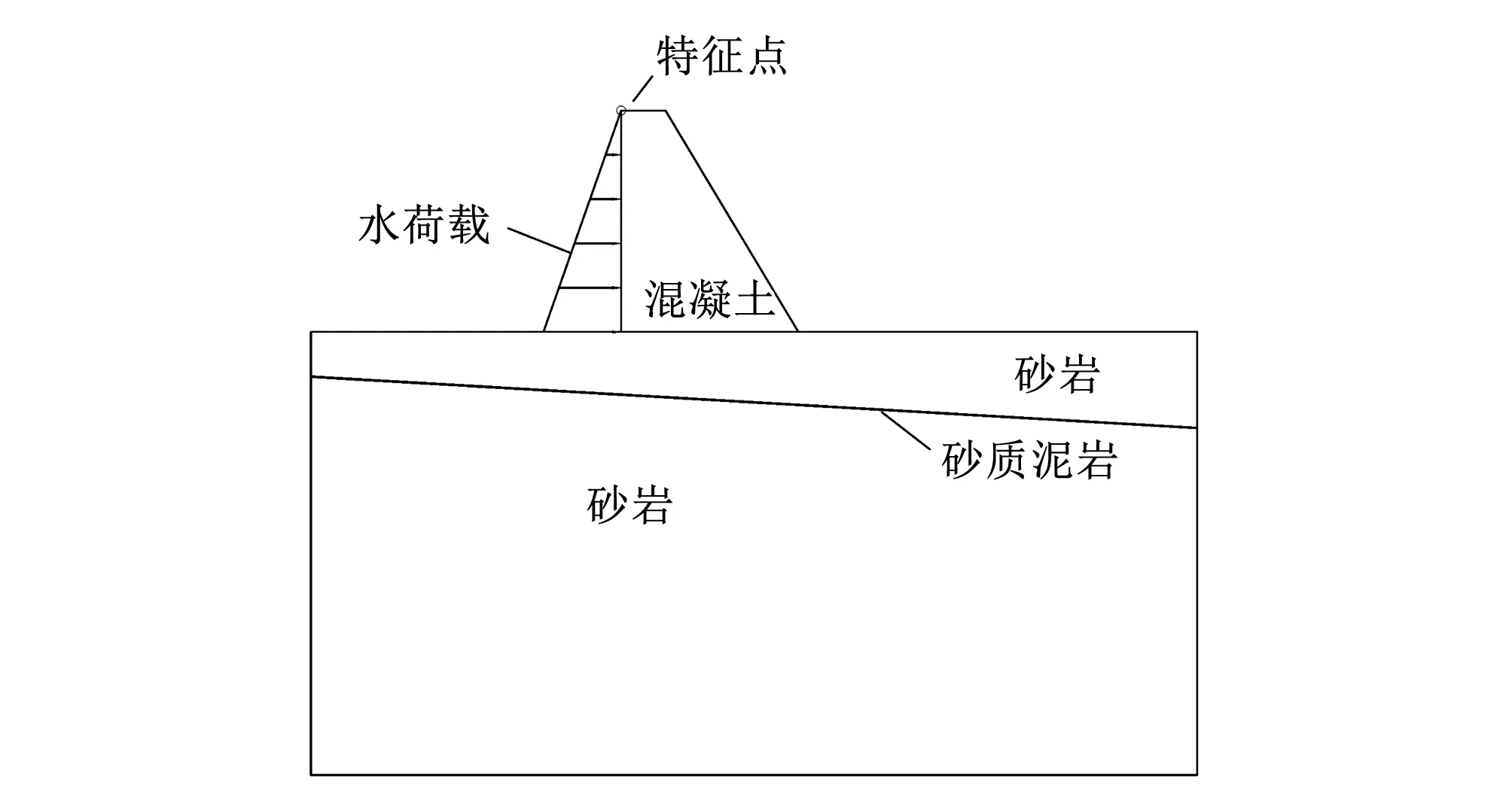
圖3 荷載施加及材料分布示意Fig.3 Schematic diagram of load exertion and material distribution

壩身混凝土始終采用線彈性材料參數，用常規的彈塑性強度折減法進行計算深層抗滑穩定性時，地基巖體均選用Mohr-Coulomb模型；用考慮蠕變的強度折減法進行計算時，對軟弱夾層的砂質泥巖及其以上部分砂巖選用Cvisc蠕變模型，下部巖體仍選用Mohr-Coulomb模型，取剪脹角ψ=φ，即采用產生最大的剪脹現象的相關聯流動法則。計算中采用的基巖材料參數見表1、表2。用FLAC3D 的Cvisc模型進行數值計算時，蠕變時間和時間步長具有真實的時間意義。算例中將最小、最大蠕變時步分別設為min dt=1×10-5、 max dt=1×10-2，計算過程中由系統根據給定的范圍自動選取蠕變步長。蠕變總時長為365 d。

表1 Mohr-Coulomb模型參數Tab.1 Parameters of the Mohr-Coulomb model

表2 Cvisc蠕變模型參數Tab.2 Parameters of the Cvisc model

2.2 數值計算及結果分析

在用常規的彈塑性強度折減法進行深層抗滑穩定計算的過程中，將命令流導入FLAC3D中，計算收斂所需的迭代步數和順河向的特征點位移隨著折減系數f的增大而增加(見圖4)，在折減系數f=4.4時迭代步數巨幅增加但仍可收斂。對不同折減系數下的特征點位移值的分析(見圖5)表明，在f=4.33時位移就已經出現拐點，并在f=4.37時明顯增大。f=4.37時的壩基塑性區分布見圖6，地基從壩體上游至下游已經發生大區域的塑性屈服。由此可見，用常規的彈塑性強度折減法計算時根據計算不收斂得到的深層抗滑穩定安全系數偏大，偏于危險，故本文由特征點位移突變和塑性區貫通的判據確定壩體的深層抗滑穩定安全系K=4.37。

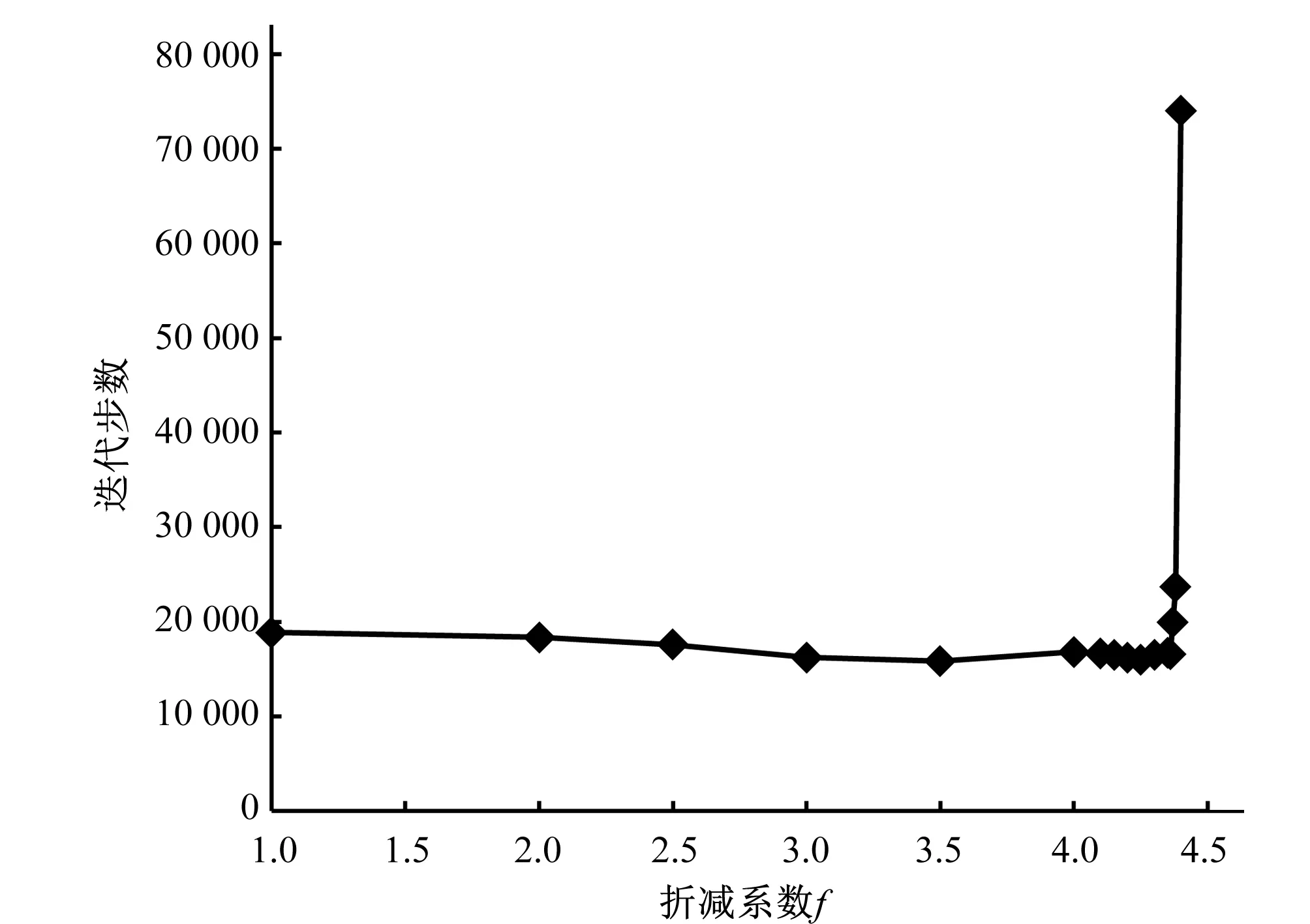
圖4 迭代步數～折減系數曲線(不考慮蠕變)Fig.4 Iteration step-reduction factor curve (creep not considered)

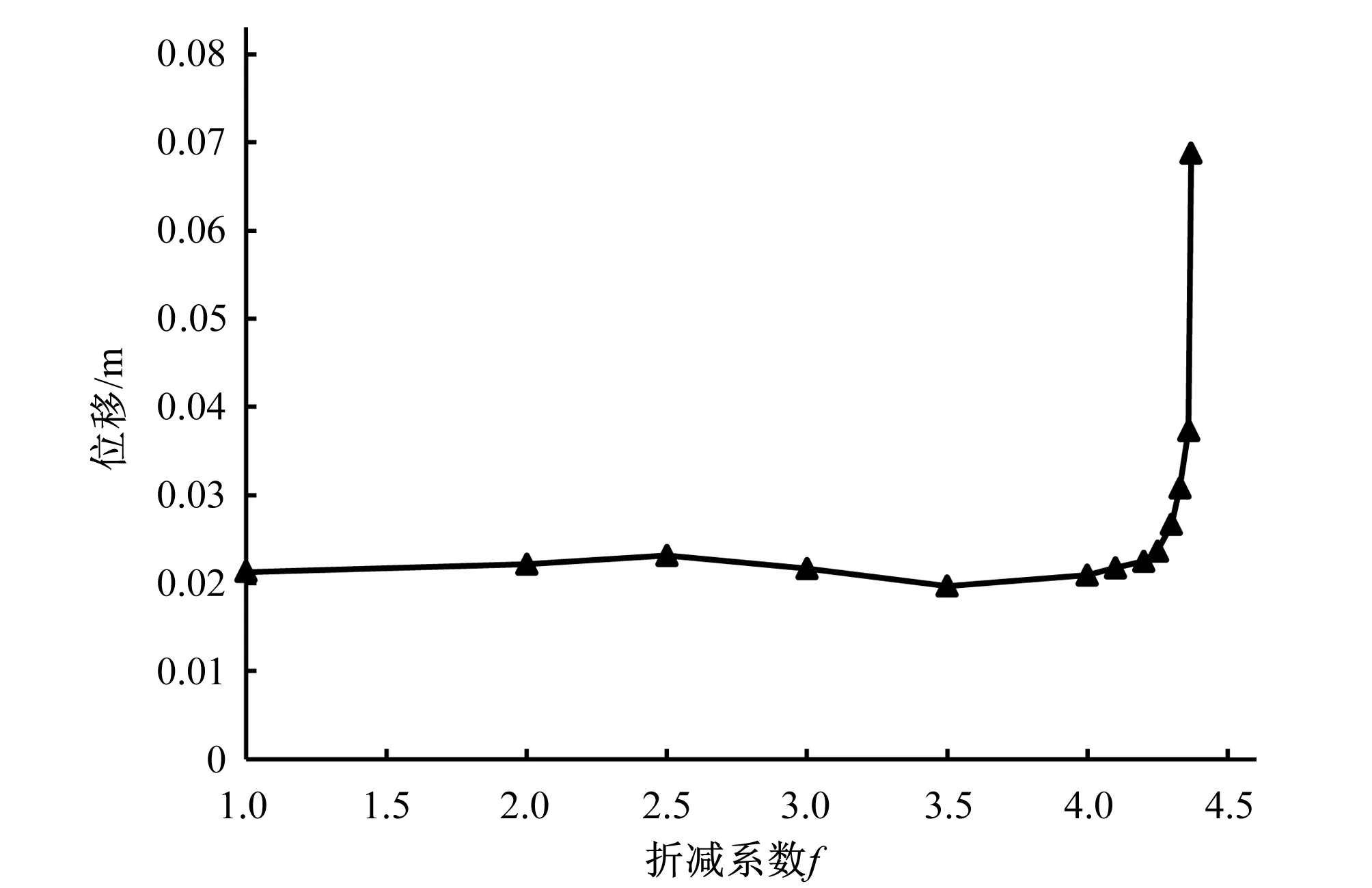
圖5 特征點位移～折減系數曲線(不考慮蠕變)Fig.5 displacement of the Characteristic point -reduction factor curve (creep not considered)

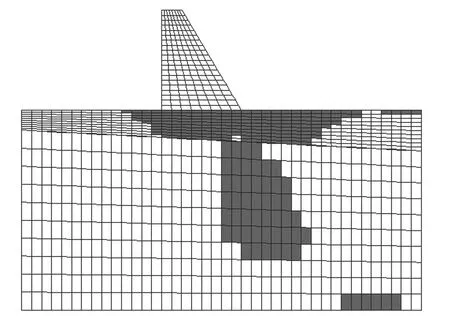
圖6 f=4.37時的模型塑性屈服狀態(不考慮蠕變)Fig.6 Plastic yielding state of the model when f=4.37 (creep not considered)

在用考慮蠕變的強度折減法計算的過程中，僅增大系數f以使抗剪參數折減，而不改變巖體的流變參數，在f增大到4.13的過程中(見圖7)，特征點的順河向位移總能在一段時間之后趨于穩定，只是位移達到穩定的時間越來越長。當f達到4.14 時，特征點位移呈現明顯增長趨勢，無法隨時間穩定。f=4.14時的壩基塑性區分布見圖8，從中可以看出，壩基已經形成了自上游至下游貫通的大面積塑性屈服區，由此可以判斷，考慮基巖蠕變的強度折減法計算得到的重力壩深層抗滑穩定系數K=4.14。

綜合以上分析可以看出，考慮蠕變后使得壩體深層抗滑穩定安全系數由用常規的彈塑性強度折減法計算得到的4.37降低為4.14，降低了5.3%，這說明基巖的蠕變特性對重力壩的深層抗滑穩定性有不利影響。考慮到深層抗滑穩定安全系數的降低幅度仍與工程允許的5%較為接近，可以認為蠕變特性的不利影響是較為有限的，但當基巖的蠕變特性明顯時，這種不利影響則必須被充分考慮。

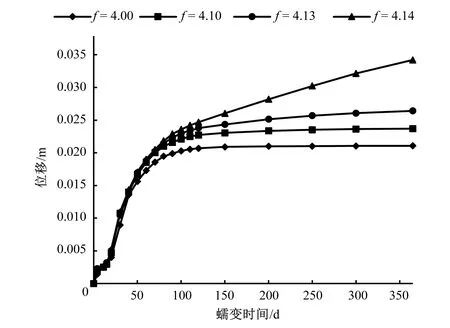
圖7 折減系數f取不同值時特征點順河向位移隨蠕變時間變化曲線(考慮蠕變)Fig,7 Displacement of the characteristic point-creep time curve when f takes different values (creep considered)

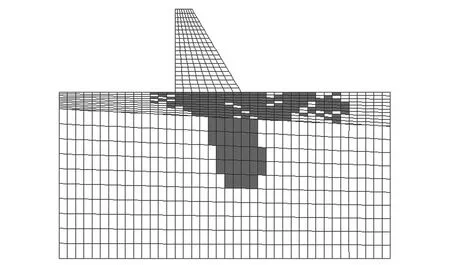
圖8 f=4.14時壩基塑性區分布(考慮蠕變)Fig.8 Plastic yielding state of the model when f=4.14(creep considered)

統計各個折減系數對應的經歷壩基365 d蠕變之后的特征點順河向位移(見圖9)，可以看出，特征點最終位移隨著折減系數先是緩慢增大，以折減系數f=4.0為拐點，隨后迅速增大，當折減系數f=4.14時位移總量為3.42 cm，而對應此折減系數下，用常規的彈塑性強度折減法計算得到的位移值為2.21 cm，即考慮蠕變后，特征點位移增大了5.4%，因此利用壩體特征點位移來預測大壩抗滑穩定性時，采取的預警指標宜比不考慮蠕變時的稍大。

圖9 特征點位移隨折減系數變化曲線(考慮蠕變)Fig.9 Displacement of characteristic point-reduction factor curve (creep considered)

3 結 論

本文以地基整體巖性較弱且帶有緩傾角軟弱夾層的重力壩為研究對象，采用考慮蠕變的強度折減法計算重力壩的深層抗滑穩定性，并與常規的彈塑性強度折減法的計算結果進行比較分析，得到如下結論。

(1)使用蠕變本構模型計算時，無法通過計算不收斂來判斷重力壩失穩，本文中將大壩特征點的位移無法隨時間穩定作為主要失穩判據，并且結合壩基塑性屈服區的發展，進行抗滑穩定安全系數的綜合確定。

(2)在同樣的折減系數下，考慮基巖的蠕變特性比僅考慮其彈塑性最終得到的壩體位移值大5.4%，因而對于對軟基上重力壩的位移監測，其預警指標宜比不考慮蠕變時的稍大。

(3)未考慮蠕變時，采用彈塑性強度折減法得到的深層抗滑穩定安全系數為4.37。考慮蠕變后，重力壩在折減系數為4.14時失穩，深層抗滑穩定安全系數降低了5.3%，說明基巖的蠕變特性會使重力壩的深層抗滑穩定性降低。當重力壩基巖的蠕變特性明顯時，工程的穩定性研究中應對巖體的蠕變特性予以充分考慮。