基于奈奎斯特定理與曲線擬合的溫度計算方法

董亞楠，黃正旺，許欽濤

（豫新汽車熱管理科技有限公司，河南 新鄉 453049）

隨著社會的進步，人們對于空調溫度控制精度的要求越來越高，而原來空調控制器中采用查表的方式進行溫度計算的溫度算法，已經不能夠適應現在空調溫度控制器系統的需求。這就要求提供一種新的算法來提高溫度計算，使其能夠適應新的溫度控制的要求。

基于奈奎斯特定理“過采樣和抽取”的方法，可以在不改變原有控制器硬件電路的基礎上，采用軟件計算的方式將MCU的AD轉換的精度在原有的基礎上提高1～2倍。這樣不僅可以提高空調溫度控制的精度，而且可以提高對空調冷暖風門、模式風門、新風門運行角度的精度，提高鼓風機反饋電壓的計算精度，有利于整個空調控制系統控制精度的提高。并且不增加產品成本和不改變空調控制器原有的硬件設計，從而能夠提高產品的市場競爭力。

1 基于奈奎斯特定理的“過采樣和抽取”

1.1 奈奎斯特定理的原理

奈奎斯特定理“過采樣和抽取”的原理：設有一個頻率帶限信號x(t)，其頻帶限制在(0，fn)內，如果以不小于fs=2fn的采樣速率對信號x(t)進行等間隔采樣，得到時間離散的采樣信號x(t)=x(nTs)(其中Ts=1/fs稱為采樣間隔)，則原有信號x(t)將被所得到的采樣值x(n)完全確定。上述的奈奎斯特采樣定理告訴我們，如果以不低于信號最高頻率2倍的采樣速率對帶限信號進行采樣，那么所得到的離散采樣就能準確地確定原信號。下面從數學的角度來進一步證明奈奎斯特采樣定理［1］。

其中x［k］=x(t)|t=Kt，Ω=ωT，連續信號x(t)的頻譜為x(jω)，離散序列x［k］頻譜為x(ejΩ)，其計算公式見公式 (1)、公式(2)、公式 (3)，如圖1所示。

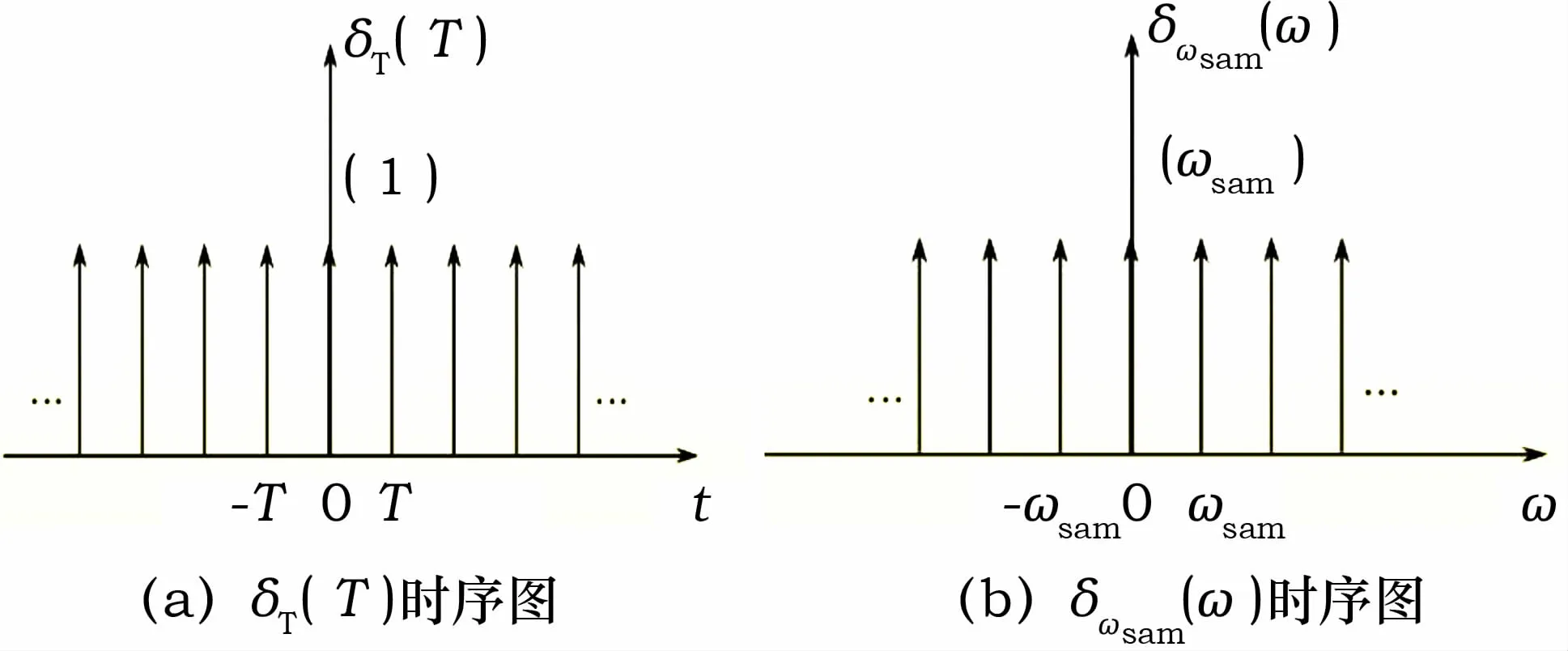
圖1 δT（T）和δωsam（ω）時序圖

若連續信號X(t)的頻譜為X(jΩ)，離散序列X［k］頻譜為X(ejΩ)，且存在x［k］=x(t)|t=Kt，則有：

信號時域的離散化導致其頻域的周期變化。其中，T為抽樣間隔，ωsam=2π／T為抽樣角頻率。X(jω)時序圖如圖2所示。當ωsam＞2ωm時，如圖3所示；當ωsam=2ωm時，如圖4所示；當ωsam＜2ωm時，如圖5所示。

圖2 X（jω）時序圖

圖3 ωsam＞2ωm時序圖

圖4 ωsam=2ωm時序圖

圖5 ωsam＜2ωm時序圖

通過公式 (1)～(7)和圖2～圖5的計算和圖示，可以得出：如果以不低于信號最高頻率2倍的采樣速率對帶限信號進行采樣，那么所得到的離散采樣就能準確確定原信號。

1.2 過采樣和抽取

現在常用的MCU產品中的ADC轉換器，轉換的ADC數據相當于一種低通濾波器，而奈奎斯特采樣定理適用于該控制器系統中。根據奈奎斯特采樣定理，如果以不低于信號最高頻率2倍的采樣速率對帶限信號進行采樣，那么所得到的離散采樣就能準確確定原信號。在進行ADC采樣時，按照公式 (8)的形式進行。其中，fsignal是輸入信號的最高頻率，fnyquist是采樣奈奎斯特頻率的“過采樣”。

根據ATMEGA644PA中數據手冊中的說明，在使用其內部10位精度的ADC轉換器時，其ADC的時鐘頻率應該在50～200 kHz，之間，本文中使用的系統時鐘為8 MHz的晶振，因此在進行ADC時鐘設定時采用64分頻，將ADC的時鐘信號圈定在125 kHz，保證其10位ADC轉換值的精確。亦在ADC轉換的硬件電路上的AVCC的ADC采樣的基準電壓輸入端采用LC濾波電路，對其進行濾波處理，并在ADC轉換期間，使用MCU的ADC轉換休眠模式 (即：定時器T0、看門狗工作，關閉其他中斷和I/O的操作，降低轉換期間的系統噪聲)［2］。

按照奈奎斯特采樣定理本文需要按照公式 (9)的形式進行，ADC轉換值的過采樣。

根據公式 (9)中的采樣頻次，如果要提高1位精度的ADC轉換值需要采集4n倍的數據來進行“過采集”。即：如果將ADC從10位提高至11位其需要過采集的數據是10位精度的4倍，將ADC從10位提高至12位其需要過采集的數據是10位精度的42=16倍。具體的計算方法是：如果將ADC10提高至ADC11，需要將4個ADC10相加，這樣就可以得到12位的ADC數值，其最后一位沒有實際意義；需再將其右移一位或者除以2，這樣就可以得到ADC11的數據。而將ADC10提高至ADC12，需要將16個ADC10相加，這樣就可以得到14位的ADC數值；其最后兩位沒有實際意義，需再將其右移兩位或者除以4，這樣就可以得到ADC12的數據，這樣每一位的電壓分辨率可以達到1.22 mV。

這樣可以得到公式 (10)用于通過計算增加ADC的分辨率［3］。

2 曲線擬合的溫度計算

2.1 基于曲線擬合的溫度計算

現在空調控制器系統中一般使用的非線性的NTC型負溫度系數的溫度傳感器，其在某溫度下的阻值計算公式如公式 (11)所示。

式中：RT1——熱敏電阻在T1溫度下的阻值；RT2——熱敏電阻在T2常溫下的標稱阻值；B——熱敏電阻的熱敏指數；T1、T2——開爾文溫度。

由于NTC型負溫度系數的溫度傳感器的熱敏指數在不同的溫度區間其數值也會隨著溫度區間地上升而加大，溫度區間地下降而減少的變化，因此NTC型負溫度系數的溫度傳感器的R-T曲線為曲值不定的一條曲線段 (如圖6所示，為本文用NTC型熱敏電阻的R-T曲線)，而使用公式 (11)計算溫度，就需要對各個溫度區間的熱敏系數進行計算，而只使用廠家提供的B值就會出現其溫度曲線在一定溫度下偏差過大的現象 (如圖6所示，其中紅色曲線為正確的R-T曲線，綠色曲線為使用公式 (11)計算的到的曲線，可以看出在系統溫度低于10℃時，2條曲線的偏差將逐漸變大)，無法滿足溫度控制精確的需要。

因此，本文為解決以上問題，首先采用的是利用傳感器廠家提供的R-T溫度表格，建立一個對應的ADC數值表，通過和表格內的數值對應，找到ADC值處于那2個整度溫度之間，然后將相鄰溫度的曲線段看做是一條直線，使用直線段的計算公式來計算溫度。但是通過這樣的方法進行計算時，分段模擬出的直線段不能與溫度傳感器的曲線完全貼合在一起，就會造成溫度計算的偏差，而且在曲線曲度越大的溫度區間內的偏差將會越大，很難達到精確控制溫度的系統要求［4］。因此，在本文中采用曲線擬合的方法來進行溫度計算。將圖6所示的紅色NTC溫度傳感器的R-T溫度曲線分成數段，然后使用其他的曲線，并取其他曲線中與目標曲線中相符合的部分，利用數條曲線來模擬出與圖6所示的紅色NTC溫度傳感器相符合的曲線段。

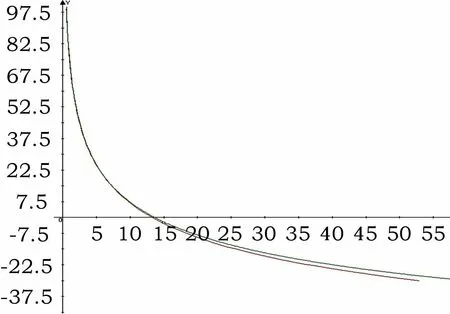
圖6 NTC型熱敏電阻與公式（11）R-T曲線圖

曲線擬合的擬合曲線的公式如公式 (12)所示，其中T為換算出的溫度值，An、An-1、An-2、…、A2、A1、B為根據不同傳感器阻值的換算常數，R為NTC傳感器的阻值。

采用公式 (12)的數列，可以分段將數列的曲線的部分與目標曲線的部分擬合在一起。本文中采用的NTC型負溫度系數的熱敏電阻的傳感器，參數為B25/50=3274、R25=5 kΩ。

通過計算和模擬，在本文中將目標曲線分為三段，分別是：T1為-40～0℃、T2為-5～60℃、T3為55～90℃。然后根據目標曲線的各個R-T溫度表的數值，計算的曲線公式如公式(13)～公式 (15)所示。其與目標曲線的擬合如圖7所示。

圖7中黃色曲線為公式 (15)的曲線，紅色曲線為公式(14)的曲線，綠色曲線為公式 (13)，圖中的藍色曲線為目標曲線。各個曲線通過與目標曲線的R-T溫度阻值表進行計算其得到的數值與目標曲線相差0.1℃。

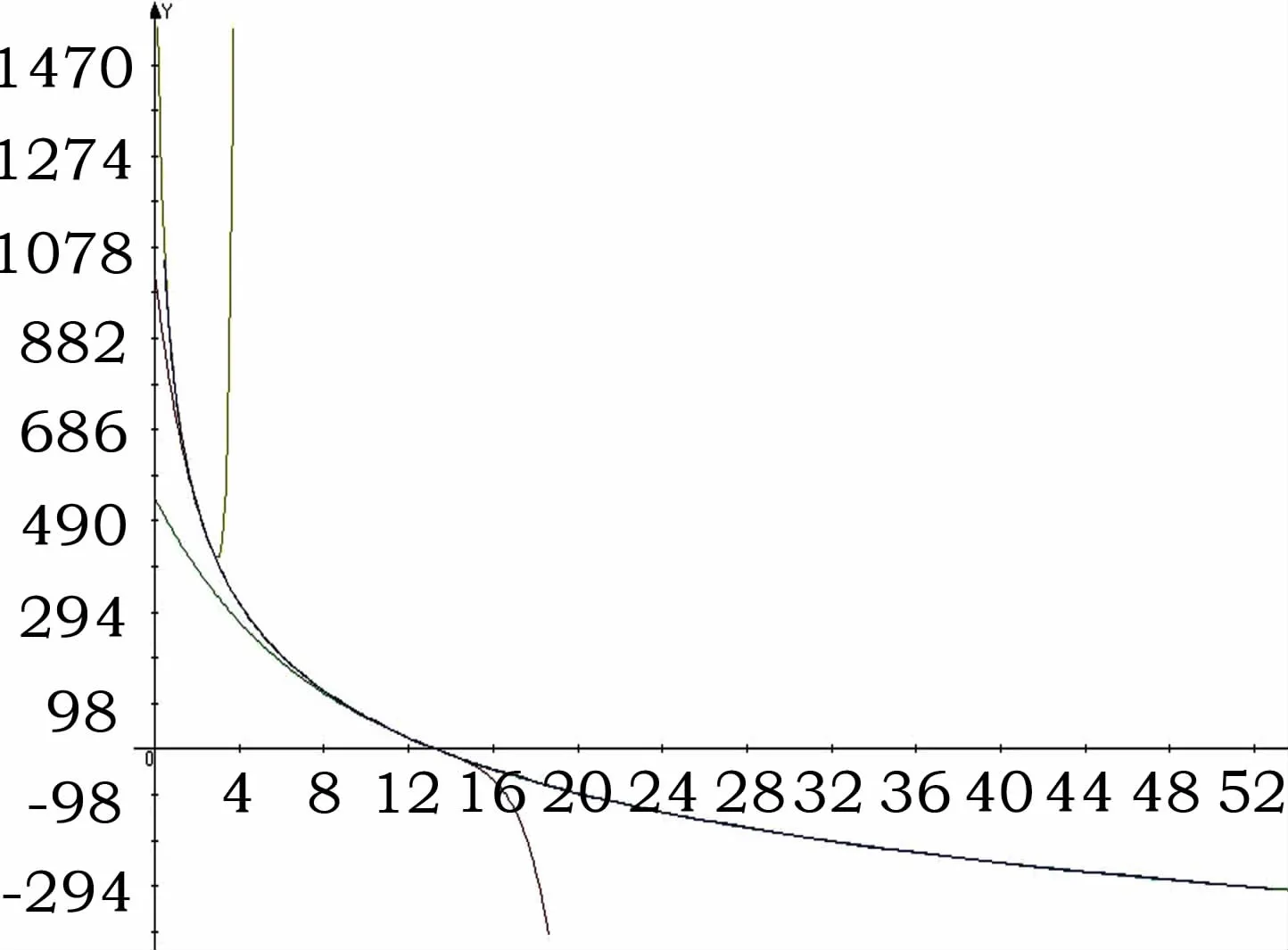
圖7 溫度傳感器R-T曲線與公式（13）～公式（15）擬合曲線圖

3 計算原理試驗驗證

本文介紹了基于奈奎斯特定理“過采樣和抽取”原理與采用“曲線擬合”方式的溫度計算方法，在不改變原有控制器系統硬件電路和系統整體成本的基礎上，通過軟件計算的方法提高了控制器對于溫度控制的精度，并且該方法還可以應用在提高空調系統。對于冷暖風門、模式風門、新風風門的角度控制精度、蒸發風機的風量調整方面的精度等，有著巨大的應用潛力。

本文使用冷藏機組用控制器來測試該溫度方法的準確性，如圖8所示，通過酒精恒溫槽如圖9對控制器的溫度顯示進行測試。

圖8 檢測控制器圖

圖9 低溫恒溫槽圖

通過測試其測試數據，如表1所示，其溫度偏差為0.1℃，達到設計要求。

表1 恒溫槽測試對比 單位：℃

4 結語

本文基于奈奎斯特定理“過采樣和抽取”原理與采用“曲線擬合”計算方式，可以精確、有效地提高MCU中ADC的轉換精度，并使得控制器的溫度計算精度達到控制器設計需求±0.1℃的精度。其提高ADC轉換精度的方法可以應用在其他高精度的控制領域中，具有極大的應用前景，而“曲線擬合”的計算可以擴展至其他非線性控制領域中，提高整體的控制精度。