軸頸表面粗糙度對橡膠材料干摩擦特性的影響*

(1.西安科技大學(xué)工程訓(xùn)練中心 陜西西安 710054；2.西安科技大學(xué)理學(xué)院 陜西西安 710054)

船舶艉軸與橡膠軸承摩擦副在運行時，軸承啟閉時出現(xiàn)的過載、重載及螺旋槳的重力引起的艉軸彎曲，均會引起軸與橡膠軸承的局部接觸，使得軸與軸承處于干摩擦狀態(tài)下，導(dǎo)致潤滑不足，磨損加劇，引起系統(tǒng)的振動及噪聲，造成系統(tǒng)的損傷事故。

國內(nèi)外學(xué)者對金屬軸頸-橡膠軸承摩擦副在潤滑條件下的摩擦磨損性能進行了大量的研究，取得了一些成果，如國外學(xué)者BRODSKII和CHARRIER等[1-2]發(fā)現(xiàn)了高分子材料磨損橡膠的特殊現(xiàn)象。近年來，國內(nèi)外學(xué)者應(yīng)用試驗和數(shù)值模擬的手段分析了表面形貌對彈流潤滑區(qū)域、混合潤滑區(qū)域和接觸區(qū)域的潤滑特性及摩擦磨損特性的影響。何仁洋、柳瓊俊等[3-4]通過實驗方法探討了干摩擦和邊界潤滑條件下橡膠對金屬的摩擦磨損機制；REN、KRUPKA等[5-6]討論了表面粗糙對潤滑膜形成的影響，認為通過合理設(shè)計粗糙度的表面紋理可提高表面潤滑性能；WANG等[7]通過反復(fù)試驗點接觸下表面粗糙度對滑動摩擦的影響，發(fā)現(xiàn)橫向紋理比縱向紋理的摩擦因數(shù)小；LITWIN等[8-10]采用試驗方法研究了不同表面形貌和不同材料下的水潤滑軸承流體動力學(xué)潤滑特性；CHOO等[11]開發(fā)了一種新的試驗方法來研究表面粗糙度對潤滑膜分布的影響；ZHANG等[12]分析了表面粗糙度對彈塑性接觸力學(xué)性能的影響；范曉夢等[13]分析了瞬變載荷作用下水潤滑軸承彈流潤滑性能分析；張闊[14]利用數(shù)值模擬方法研究了材料的表面形貌對混合潤滑下摩擦性能的影響。最近，楊勇等人[15]基于快速傅立葉變換的數(shù)值仿真方法生成了給定參數(shù)分布的非高斯曲面，求得了不同表面粗糙度特征下的齒輪接觸區(qū)域潤滑特性；劉明勇等[16]探討了二維規(guī)則下表面粗糙度的波長、幅值及工況變化下的潤滑特性；GHERCA、WANG等[17-18]通過數(shù)值模擬和實驗相結(jié)合的方法，通過優(yōu)化推力軸承的表面紋理提高了軸承的流體動力學(xué)及摩擦潤滑特性；ZHU和HUANG[19]基于軸承曲率的形貌參數(shù)對摩擦磨損性能做了探討。

上述研究主要集中在金屬軸頸表面粗糙度對軸承潤滑膜的形成及潤滑性能的影響，但研究金屬軸頸表面粗糙度對橡膠軸承-軸頸摩擦副干摩擦特性影響的文章較少。為研究軸頸表面粗糙度對水潤滑橡膠軸承在干摩擦狀態(tài)下摩擦特性的影響，本文作者采用試驗與理論計算相結(jié)合的方法，探討金屬軸頸-橡膠材料摩擦副干摩擦狀態(tài)下摩擦因數(shù)的計算方法，為水潤滑橡膠軸承摩擦性能的研究提供依據(jù)。

1 數(shù)學(xué)模型

1.1 粗糙剛性表面與橡膠材料的接觸模型

船舶艉軸與橡膠軸承在相對運動時，當(dāng)軸承供水系統(tǒng)出現(xiàn)故障或軸承過載時，軸頸與橡膠軸承之間會發(fā)生局部接觸。從微觀來看，任何真實的工程表面都不是絕對光滑的，而是存在一定的粗糙度[20]，這個粗糙度使得兩物體之間的接觸變成微凸體之間的接觸。

圖1所示為粗糙剛性表面與橡膠材料的接觸模型，橡膠在一個粗糙表面上滑動，在此情況下，摩擦力主要取決于金屬表面的粗糙度，橡膠表面粗糙度所起作用很小，因此問題可以簡化為光滑橡膠與粗糙金屬之間的摩擦。由于在局部接觸時橡膠軸承和軸頸之間存在納米尺度的薄膜[21-22]，可假設(shè)橡膠材料和軸頸之間無黏著力，此時滯后摩擦起主要作用，即滑動橡膠材料在周期變形過程中產(chǎn)生的能量損耗，此時問題就轉(zhuǎn)化為計算橡膠材料的變形和能量損耗[20]。

圖1 粗糙剛性表面與橡膠材料的接觸模型

1.2 表面粗糙度的參數(shù)表征

表面形貌通常以表面粗糙度的分布形式表征，因此金屬的表面粗糙度分布是研究的重點。

圖2 微凸體的表面分布模型

(1)

一個微凸體的特征直徑[20]：

(2)

微凸體接觸的單位體積能量損耗[20]：

(3)

1.3 摩擦因數(shù)

摩擦因數(shù)[20]：

μ=ζ

(4)

μ≈z

(5)

2 試驗方法

2.1 試驗材料

以某水潤滑橡膠軸承主軸為測量對象，利用TIME3230表面粗糙度測量儀對金屬軸徑表面的微凸體位置分布參數(shù)進行測量。軸頸的材料為40Cr，表面粗糙度為Ra0.8 μm，調(diào)質(zhì)處理，表面磨削。

2.2 測量方法

采用圖3所示TIME3230表面粗糙度測量儀對沿加工紋理方向、垂直于加工紋理方向及與加工紋理方向呈45°夾角方向的金屬軸頸表面的微凸體高度分布進行測量。

圖3 TIME3230表面粗糙度測量儀

微凸體位置分布參數(shù)的測量原理如圖4所示，粗糙度形狀測量儀采用大量程的差動電感傳感器拾取被測信號，測量軸表面時，將傳感器放在軸表面上，由驅(qū)動器帶動傳感器沿軸表面做等速滑行，驅(qū)動器中的導(dǎo)軌保證軌跡的精度。傳感器通過銳利的金剛石觸針感受被測表面的輪廓信號，此時軸表面輪廓起伏引起觸針產(chǎn)生垂直位移，并輸出運行軌跡垂直位移的坐標。

測量方法：軸頸低速運動，在恒定載荷下，采用表面粗糙度形狀測量儀沿軸頸的加工紋理方向、垂直加工紋理方向及與加工紋理呈45°夾角方向共3個方向進行數(shù)據(jù)采集。每個方向采集4組數(shù)據(jù)，每隔0.001 μm設(shè)置一個數(shù)據(jù)采集點采集數(shù)據(jù)一次，取樣長度為0.8 mm，評定長度取5倍的取樣長度。最終得到12組金屬軸徑表面微凸體位置分布數(shù)據(jù)。

3 結(jié)果與討論

3.1 表面粗糙度原始數(shù)據(jù)的去噪處理

取沿軸頸加工紋理方向的原始測量數(shù)據(jù)2組，如圖5所示。它包含一定的隨機噪聲，同時，機械加工零件表面存在較大的各向異性，這些都使得測量的表面數(shù)據(jù)應(yīng)用較為困難。因此，采用Savitzky-Golay算法進行平滑去噪，有效去除測量信號中的脈沖噪聲和白噪聲，去噪后的結(jié)果如圖6所示，它是一系列隨機的表面波，且可以看出去噪后的數(shù)據(jù)保有效保留了原始數(shù)據(jù)的特征。

圖5 沿加工紋理方向的粗糙度原始數(shù)據(jù)分布曲線

圖6 去噪后的沿加工紋理方向的粗糙度數(shù)據(jù)分布曲線

3.2 計算模型的建立

任何連續(xù)的時序或信號，都可以表示為不同頻率的正弦波信號的無限疊加，因此傅立葉變換可以將表面粗糙度儀測得的隨機表面波分解為有一定規(guī)律的正弦波分量的組合。利用Matlab軟件中的傅立葉擬合函數(shù)將去噪后的原始數(shù)據(jù)進行擬合變換，經(jīng)過傅立葉擬合變換后重新構(gòu)造的軸頸表面粗糙度分布表達式f(x)為

(6)

式中：A為波幅；k為特征波波長，令λ=1/k為波長系數(shù)。

3.3 計算模型的驗證

采用7階傅立葉變換，將去噪后的數(shù)據(jù)進行變換處理，得到粗糙度分布結(jié)果如圖7所示。

圖7 采用傅立葉變換后的沿加工紋理方向的粗糙度數(shù)據(jù)分布曲線

觀察采用傅立葉變換后的曲線分布可發(fā)現(xiàn)，新擬合的曲線與去噪后的原始數(shù)據(jù)非常接近，可以真實地反映粗糙軸表面的粗糙度輪廓特點。因此軸頸的表面粗糙度分布可以看作是7個正弦函數(shù)和7個余弦函數(shù)的疊加，因此它們對摩擦因數(shù)的貢獻相加等于[20]：

(7)

不同潤滑狀態(tài)下的摩擦因數(shù)如表1[24]所示。將采用傅立葉變換后的各項系數(shù)代入摩擦因數(shù)計算表達式(7)，得μ=0.167 2。由表1可以判斷此時的潤滑狀態(tài)處于干摩擦狀態(tài)，這與實際情況吻合。

表1 不同潤滑狀態(tài)下的摩擦因數(shù)

3.4 粗糙度幅值和特征波波長系數(shù)對摩擦因數(shù)的影響

在軸頸轉(zhuǎn)速一定的情況下，利用式(7)計算了在不同粗糙度幅值0.5A、A、1.5A、2A、2.5A和不同特征波波長系數(shù)0.5λ、λ、1.5λ、2.0λ、2.5λ下的摩擦因數(shù)，結(jié)果如圖8所示。

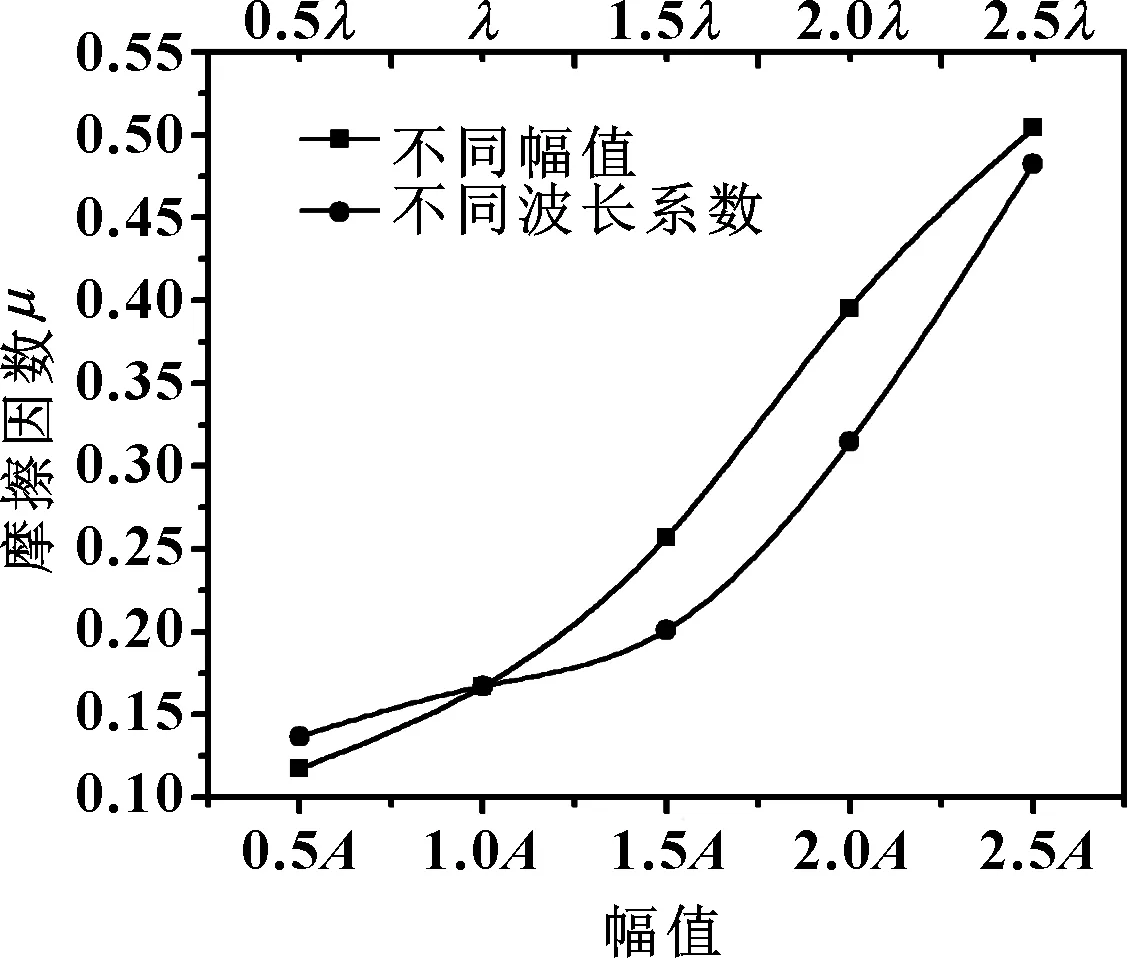
圖8 不同幅值和特征波波長系數(shù)下的摩擦因數(shù)

由圖8可以看出：隨粗糙度函數(shù)幅值從0.5A逐漸增加到2.5A，摩擦因數(shù)從0.130 9增加到0.543 4，這是由于隨著微凸體粗糙度函數(shù)幅值的增大，加工表面越粗糙，微凸體特征高度的正負高差越大，微凸體表面均方根l變大，使得表面輪廓梯度的平方根z也增大，摩擦因數(shù)增大；隨粗糙度波長系數(shù)從0.5λ逐漸增加到2.5λ，摩擦因數(shù)從0.157 2增加到0.496 8，這是由于隨著特征波波長系數(shù)的增大，表面微凸體的密度變大，表面間的接觸面積增大，表面輪廓梯度的平方根z也增大，使得摩擦因數(shù)增大。

3.5 加工紋理對摩擦因數(shù)的影響

在實際工程中，表面紋理方向多與潤滑流動方向呈一定夾角。采用表面儀測量了與加工紋理方向呈45°夾角和垂直加工紋理方向的粗糙度，并進行傅立葉變換構(gòu)造處理，利用公式(7)計算出這2個不同方向下的摩擦因數(shù)，并與順加工紋理方向的摩擦因數(shù)進行比較，如表2所示。

表2 不同紋理下的摩擦因數(shù)

由表2可以看出：潤滑流動方向順著加工紋理方向時摩擦因數(shù)最小，垂直加工紋理方向時摩擦因數(shù)最大。這是由于潤滑流動方向順加工紋理方向時，微凸體特征高度正負高差較小，同時微凸體密度也較小，波動的幅值和特征波長均較小，使得z變小，摩擦因數(shù)變小；而垂直加工紋理時，微凸體特征高度正負高差較大，同時微凸體密度也較大，波動的幅值和特征波長均較大，使得z變大，摩擦因數(shù)變大；當(dāng)與加工紋理方向呈45°時，微凸體特征高度和密度均居于二者之間，因此其摩擦因數(shù)大于順加工紋理方向的摩擦因數(shù)，小于垂直于加工紋理方向的摩擦因數(shù)。

因此，選擇合理的軸承表面粗糙度函數(shù)的幅值和波長可以提高金屬軸頸-橡膠軸承摩擦副的摩擦潤滑性能；同時，沿加工紋理加工、裝配金屬軸頸-橡膠軸承摩擦副，可降低摩擦因數(shù)，從而有效避免軸承的打滑擦傷失效。

4 結(jié)論

(1)在干摩擦狀態(tài)下，水潤滑橡膠軸承-軸頸副的摩擦因數(shù)隨表面粗糙度函數(shù)幅值的增大而增大，且隨著粗糙度函數(shù)特征波長系數(shù)的增大非線性增加。潤滑流動方向順著加工紋理方向時摩擦因數(shù)最小，潤滑流動方向與加工紋理方向呈45°時摩擦因數(shù)次之，潤滑流動方向垂直加工紋理方向時摩擦因數(shù)最大。

(2)利用傅立葉變換重新構(gòu)造表面粗糙度分布模型，并依據(jù)理論計算橡膠材料-軸頸副的摩擦因數(shù)，計算結(jié)果與實際情況吻合，驗證了模型的正確性。

(3)研究表明：選擇合理的軸承表面粗糙度函數(shù)的幅值和波長可以提高金屬軸頸-橡膠軸承摩擦副的摩擦潤滑性能；同時，沿加工紋理加工、裝配金屬軸頸-橡膠軸承摩擦副，可降低摩擦因數(shù)，從而有效避免軸承的打滑擦傷失效。上述試驗研究可為后續(xù)研究分析水潤滑橡膠軸承的動力學(xué)特性提供理論依據(jù)。