雙樹復小波域馬爾科夫的遙感圖像分割方法

汪匯兵，范奎奎，歐陽斯達，戚凱麗，楊朦朦

(1.自然資源部國土衛星遙感應用中心，北京 100048；2.中國礦業大學，江蘇 徐州 221000；3.山東科技大學，山東 青島 266510)

0 引言

遙感圖像分割作為信息提取、地物分類與特征識別的重要環節，是遙感圖像處理技術研究的熱點和難點之一[1-3]。隨著遙感圖像空間分辨率的不斷提高，紋理細節信息越來越豐富，地表覆蓋愈加復雜多樣，像素空間相關性愈發復雜，影像灰度、噪聲等不確定性增加，一方面對遙感圖像分割在區域細節信息上的精度要求越來越高，另一方面灰度不均、噪聲、地物邊緣混疊等現象對分割的影響越來越大。

聚類方法作為常用的基于像元的圖像分割算法，是根據圖像像元灰度的不同將圖像內的各像素劃分到預先設定的幾種不同類別中，然后將屬于同一類別且相互連通的像素合并為同一個區域[4-6]，具有算法實現簡單，迭代收斂速度快的特點。常用的聚類方法包括有K均值(K-means)[7-9]，模糊C均值(fuzzy C-means，FCM)[10-12]，期望最大化法(expectation-maximization，EM)[13]等，但此類方法都只是在單一尺度上進行，且沒有考慮像素與鄰域之間的關系，對于具有復雜信息的高分辨率遙感圖像的分割，易受噪聲、地物邊界混疊和灰度不均勻的影響，且易丟失目標的細節信息，引起誤分割問題，分割細節精度和魯棒性欠佳。

由于馬爾科夫隨機場(Markov random field，MRF)模型具有能夠很好刻畫圖像信息的空間相關性并能有效建立上下文的先驗模型的特性，基于MRF模型的分割算法已經廣泛應用于圖像分割中[14-15]，以解決傳統聚類方法存在的問題。文獻[16]結合分數階微分理論提出了一種MRF紋理圖像分割模型，并通過對比試驗驗證了基于MRF的分割方法能夠較好彌補FCM法僅利用灰度信息，對像素空間信息描述不完善的缺陷。文獻[17]提出了一種基于模糊馬爾可夫隨機場的無監督遙感圖像分割算法，結合FCM的模糊性和MRF的空間相關性，并考慮圖像的灰度特征和紋理特征，使分割結果更加準確，但是這類方法任只在單一尺度上進行，對于圖像的邊緣、細節及突變信息表達較弱，而且難以較好地克服影像噪聲的影響。

而小波分解具有多尺度分析特性，基于小波分解的多尺度分割算法[18]，可以提升分割的邊緣精度與細節表達。文獻[19]提出了一種基于小波變換的多分辨率圖像分割方法，將小波的多尺度分析與形態學方法相結合較好地減少圖像過分割現象。文獻[20]提出了一種帶有邊界的小波域Markov模型圖像分割算法，并通過對醫學圖像的試驗，證實了它不僅能有效地區分不同區域，而且可以很好地保留邊界信息。文獻[21]將雙樹復小波變換(dual-tree complex wavelet transform，DT-CWT)與MRF模型相結合對紋理圖像和遙感圖像進行分割，由于DT-CWT具有逼近的移不變性、更多的方向選擇性和完全重構的性質，進一步提高了基于離散小波與MRF分割算法的分割精度，但這類方法忽略了高分辨率遙感圖像的不確定性，對于圖像的模糊問題，如地物邊界混疊，灰度不均勻等分割效果不佳，且未考慮圖像噪聲對分割的影響。文獻[22]提出了一種基于DT-CWT的模糊聚類分割方法，在DT-CWT域內利用改進的FCM分割算法對紋理圖像及航片進行分割，利用DT-CWT較好地提高了FCM分割算法的邊緣準確性、區域一致性和分割精度，同時利用FCM的模糊性在分割中較好地處理了地物邊緣的混疊，明顯減少了斑點噪聲，但是這類方法都是在假設像素獨立的前提下進行的，并未考慮像素間的相關性，邊緣分割粗糙，誤分像素較多。

為了提高分割方法的細節精度和魯棒性，綜合考慮圖像分割的多尺度性、模糊性及像素的空間相關性，本文結合雙樹復小波變換DT-CWT的多尺度和多分辨率特性、模糊馬爾科夫隨機場(fuzzy Markov random field，FMRF)模型中FCM的模糊性以及MRF的像素空間相關性，提出了一種非監督遙感圖像分割方法，簡稱為DTCWT-FMRF。該方法首先采用DT-CWT對圖像進行多尺度分解，準確表達高分辨率遙感圖像的細節信息，并利用貝葉斯(Bayesian)閾值對高頻分量進行濾波處理，進一步去噪和突顯細節信息，提高方法的抗噪性。然后為了避免由于不同層分量的尺寸不同引起分割邊緣的模糊，重構處理后的相應層高、低頻分量，并充分考慮圖像分割的模糊性和像素鄰域間的相關性，在FCM初始分割下建立MRF模型，再根據最大后驗概率準則(maximum a posterior，MAP)實現各層的最優分割。最后根據相似度融合規則融合各層分割結果，進一步提高分割細節精度，得到最終的分割結果。并通過與多種常用的聚類方法分割結果進行定量比較，分析算法的優缺點。

2 DT-CWT和FMRF分割模型

2.1 DT-CWT分解

DT-CWT是將復小波實部和虛部的生成分開來實現，是通過兩組并行的實數濾波器組來分別獲取復小波的實部變換系數和虛部變換系數。DT-CWT不僅繼承了傳統離散小波變換(discrete wavelet transform，DWT)良好的時頻分析能力，最主要的是具有近似的平移不變性和更多的方向選擇性，以及彌補了復小波不能完全重構的缺陷[23]。為了克服奇/偶(odd/even)濾波器因嚴格線性相位引起的采樣結構差異的缺點，本文采用Kingsbury提出的基于正交變換的(quarter sample shift，Q-Shift)濾波器組[24]對圖像進行DT-CWT分解，每層分解可得到1個低頻子帶和6個方向(±15°，±45°，±75°)的高頻子帶。如圖1所示為三層DT-CWT分解示意圖，其中X為原始圖像，X(n)(n=1，2，3)為第n層分解的高、低頻子帶。圖中陰影部分為低頻子帶，空白部分為高頻子帶。

圖1 三層DT-CWT分解樹狀圖

2.2 FMRF圖像分割模型

(1)

(2)

argmaxP(W=w|F=f)∝
argmin(U(w)+U(w，f))

(3)

式中：U(w)為標記場能量，U(w，f)為特征場能量。從公式(3)可以看出，最終的能量大小由標記場能量和特征場能量共同決定的。由于 ICM易收斂到局部能量最優解，分割效果依賴初始標記場狀態[27]，本文采用FCM聚類算法對ICM的初始標記場進行模糊化。

3 結合DT-CWT和FMRF的圖像分割算法

3.1 算法流程

綜合考慮高分辨率遙感圖像的尺度層次、算法復雜度，本文選擇進行3層DT-CWT分解和FMRF結合進行試驗，算法流程圖見圖2所示。

圖2 基于DT-CWT和FMRF的圖像分割流程圖

假設X是待分割的遙感圖像對應的灰度矩陣，具體算法實現步驟如下：

步驟1對X進行三層DT-CWT分解，每層分解可分別得到1個低頻子帶記為{L1，L2，L3}帶和6個方向的高頻子帶記為Hk，l，(k=1，2，3；l=±15°，±45°，±75°)；

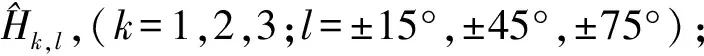
步驟4分別對C1、C2、C3進行基于自適應Bayesian閾值的 FCM初始分割，得到初始分割狀態，為W1、W2、W3；

步驟5基于MRF與GRF的等價性，利用ICM迭代模型不斷迭代更新分割狀態，達到最終的最優分割Z1、Z2、Z3；

步驟6根據定義的相似度融合規則，對Z1、Z2、Z3進行融合，即得到最終分割結果Z。

算法中，FCM循環終止條件選擇為相鄰兩次循環聚類中心差值均小于0.000 1，最大迭代次數為15次，ICM最大迭代次數設置為30次。

3.2 高頻分量處理

經過三層尺度分解后，遙感圖像分解的各層低頻分量承載著圖像的亮度或灰度變化緩慢的區域信息，描述了圖像的主要能量；而各層高頻分量承載圖像的突變信息，如圖像邊緣、輪廓信息及大部分噪聲信息。為了平衡高分辨率遙感圖像分割中噪聲的去除和高頻細節信息較好地保留，在3.1節步驟2中，

首先對高頻復小波系數的實部和虛部分別進行Bayesian閾值濾波處理，然后將各層處理后的實部和虛部對應相加組合成復小波系數來實現。具體算法實現示意圖如圖3所示。

圖3 高頻分量處理過程示意圖

以印度尼西亞英德地區Landsat-8衛星影像為例，圖4為經過DT-CWT分解得到的第一層復高頻子帶圖像，從左到右分別表示-75°、-45°、-15°、15°、45°、75°方向的高頻信息；圖5為經過Bayesian閾值濾波處理后的第一層復高頻子帶圖像。可以看出經過Bayesian閾值濾波處理后的高頻分量，雜點更少，能量更加集中。

圖4 第一層復高頻子帶圖像

圖5 經Bayesian閾值濾波處理后的第一層復高頻子帶圖像

3.3 FMRF分割模型

由文獻[27]可知MRF分割中的ICM迭代易收斂到局部能量最優解，分割效果非常依賴初始分割條件，通常選擇K-means分割算法作為圖像的初始分割方法。但經過歸一化后進行DT-CWT分解得到的各高、低頻子帶系數都很小，由灰度直方圖來確定K-means初始聚類中心不僅困難，且效果不佳。故本文采用FMRF分割模型，即用FCM聚類算法對圖像進行初始分割，并由Bayesian閾值確定初始聚類中心，不僅解決了高分辨遙感圖像的聚類中心確定困難問題，而且可以避免K-means的硬分割問題。

假設待分割圖像灰度矩陣為X(i，j)，設定聚類數為3且只考慮二階鄰域系統，FMRF的ICM迭代算法具體步驟如下：

步驟1對X(i，j)求取Bayesian閾值level1將X(i，j)分為兩類，并對方差較大的類再次求Bayesian閾值level2，然后根據v1=(min(D(i，j))+min(level1，level2))/2，v2=(level1+level2)/2，v3=(max(D(i，j))+max(level1+level2))/2求取初始聚類中心V=[v1，v2，v3]；

步驟2計算FCM的隸屬度矩陣U，并根據U更新標記場Wm和聚類中心Vm，其中m為迭代次數；

步驟3設定迭代總次數，重復步驟2不斷對標記場Wm進行迭代更新；

步驟6判斷循環終止條件(迭代終止條件設置為30次)，重復步驟4、5不斷對標記場進行迭代更新，達到最終的MAP最優分割。

如圖6為經過上述基于FMRF模型得到的3個分割結果，對應3.1節步驟5中的Z1、Z2、Z3。

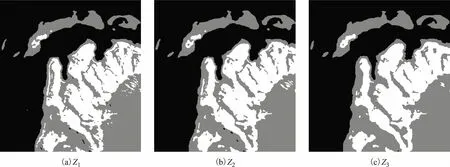
圖6 基于FMRF模型分割的三層結果

3.4 相似度融合規則

為了彌補因取交集引起的細節類別漏分現象，本文根據自定義的相似度融合規則進行融合。

首先，定義u為相似度，為了最大程度保留高分辨遙感圖像的細節信息，統計二階鄰域內與目標像素值相同的數目，記s個相同像素值，則相似度u=s，其中(0≤s≤8)且為整數。

相似度融合規則即是，統計3.1步驟5中Z1、Z2與Z3中二階鄰域內對應位置的像素的相似度u1、u2和u3，并根據u1、u2和u3的大小來確定最終劃分的類別，具體規則如下：比較分割結果Z1、Z2與Z3中對應位置的像素值，若Z1(i，j)=Z2(i，j)=Z3(i，j)，則使Z(i，j)=Z1(i，j)；否則若u1=max(u1，u2，u3)，使Z(i，j)=Z1(i，j)；若u2=max(u1，u2，u3)，則使Z(i，j)=Z2(i，j)；若u3=max(u1，u2，u3)，使Z(i，j)=Z3(i，j)，具體相似度融合規則實現流程圖如圖7所示。

圖7 融合規則示意圖

4 試驗與分析

為了檢驗所提算法的分割細節精度和魯棒性，分別選用傳統的K-means法[7]、FCM法[11]、MRF法[15]與文中所提方法DTCWT-FMRF法進行試驗和對比分析，所有算法運行環境均為Intel(R)Core(TM)i7，2.67 GHz主頻，8 GB內存，Matlab2012a。試驗圖像如圖8(a)為2014年9月30日遼寧省金州區的ZY-3衛星影像，裁剪尺寸均為384×384，圖9(a)為2013年8月3日印度尼西亞英德地區Landsat-8影像，裁剪尺寸均為382×352，圖8(b)和圖9(b)分別為其對應的參考分割圖像，是通過直接觀察原始圖像灰度差異和結合人工閾值分割結果手動提取出來的。如圖10和圖11分別為對應影像各種方法的分割結果。

圖8 遼寧省金州區ZY-3衛星影像

圖9 印度尼西亞英德地區Landsat-8影像

圖10 遼寧省金州區影像的各種算法分割結果

圖11 印度尼西亞英德地區的各種算法分割結果

由圖10和圖11可以明顯看出K-means法和FCM法分割比較分散，雜點較多，而且明顯存在過分割現象；MRF法方法分割雜點較少，但是邊緣分割參差不齊，較為粗糙；相比之下可以看出本文所提方法分割呈塊狀，雜點最少，邊緣分割較為平滑，表現出區域一致性，視覺效果較好，這是由于在本文算法中進行了雙樹復小波變換，較好地克服了傳感器噪聲和配準誤差的影響，并通過FMRF進行分割，充分考慮了高分辨率遙感影像分割的模糊性和像素間的相關性，使得分割結果表現出較好的區域一致性。

由于通常情況下，高分辨率遙感圖像噪聲表現為孤立的離散點，沒有空間關聯性，故可視為服從高斯分布[28-29]，為了更直觀驗證本文所提方法對高分辨遙感圖像分割的魯棒性，對帶有高斯噪聲的仿真圖像進行試驗，如圖12是根據高分辨率遙感圖像特性并加入方差為0.005的高斯噪聲的仿真圖像，大小為192×192，圖13為仿真圖像分割結果。可以明顯看出，對于含有噪聲的仿真圖像，本文所提方法分割較為充分，且不含雜點，去噪效果明顯。

圖12 帶有高斯噪聲的仿真圖像

圖13 4種方法仿真圖像分割結果

為了進行客觀評價，表1給出了真實影像和仿真圖像的各種方法分割結果的評價指標值，包括：總誤分像素數(overall error，OE)、正確率(overall right，OR)，以及運行時間T。設標準分割為R(i，j)，算法分割結果為Z(i，j)，圖像總像素數為n，各評價指標的計算式為：

OE=sum(R(i，j)≠Z(i，j))

(5)

(6)

式中：T為各算法變化檢測實際運行時間。

表1 4種算法分割結果性能比較

從表1可以看出，3組圖像分割試驗中聚類方法K-means 和FCM的OE相當且明顯高于基于MRF分割的方法，說明將MRF的空間像素相關性引入到高分辨率遙感圖像分割中可以大大降低像素誤分現象；另外可以看出DTCWT-FMRF法的OE最小，OR最大，說明將DT-CWT的多尺度表達特性與FCM模糊性、MRF的像素空間相關性相結合可以明顯提高影像分割精度；但從算法耗時上看，所提方法耗時最長，這是由于算法中存在DTCWT域高頻信息處理和FMRF分割模型中的多次循環迭代過程的緣故。因此以犧牲算法耗時為代價前提下，本文所提方法較傳統的K-means法、FCM法及MRF法在性能指標總誤分像素數、正確率上表現最優。

綜合主、客觀可以看出，在不考慮算法耗時情況下，本文所提方法邊緣分割更加平滑細膩，區域一致性更好，具有較好的視覺效果，同時能夠很好地抑制噪聲，具有較高的分割精度和較強的魯棒性。

5 結束語

本文提出了一種基于DT-CWT與FMRF模型相結合的非監督高分辨率遙感圖像分割算法，首先利用DT-CWT的多方向表達性、各向異性和多尺度特性對原始圖像進行多尺度分解，有助于高分辨遙感圖像細節信息的表達與分析，提高了分割精度；然后通過Bayesian閾值法對各高頻子帶進行去噪并重構相應層的高、低頻分量，較好地平衡了噪聲的去除和高頻信息的保留；最后利用基于FCM分割的ICM迭代算法對重構的各層信息進行分割，并根據所提出的相似度規則融合各層分割結果得到最終的分割結果，充分考慮了像素分割的模糊性和像素鄰域間的相關性，不僅大大降低了誤分率，而且能夠很好地去除雜點和噪聲的影響。對比試驗結果表明：基于DT-CWT與FMRF相結合的分割方法較其他3種常用聚類分割方法雜點分割較少，邊緣分割更加平滑細膩，且總錯誤數最小，正確率最高，具有較高的分割細節精度和較強的魯棒性，更適合高分辨率遙感圖像分割。由于算法中存在多次迭代過程，耗時較長分割效率較低，對于更高分辨率的圖像分割處理能力有待提升，對于如何提高算法分割效率和算法復雜度分析需要進一步的研究。