航空發動機轉子系統主動抑振控制方法研究

金福藝，李 超

（長沙航空職業技術學院，湖南 長沙 410124）

旋轉機械被廣泛應用于包括航空發動機、燃氣輪機、工業壓縮機及各種電動機等機械裝置中，在這些領域中，轉子系統的振動問題一直是關注的焦點，振動過大不僅容易引發轉子系統故障，同時也往往成為旋轉機械其他系統振動的重要激勵源[1]。因此，轉子系統的振動問題不僅關系到轉子系統自身的性能和安全，也關系到旋轉機械整機的振動響應水平和工作性能。特別對于不斷追求高可靠性、高性能的航空發動機來說，往往因為設計經驗不足或者對系統結構的力學性能認識不夠深刻，以及加工裝配工藝水平的限制，使得僅通過優化力學特征參數以減少振動帶來對結構損傷和對結構效率[2,3]減弱達不到期望的效果。

多電技術[4]在提高航空發動機性能、減少燃料消耗和改善維護性能等方面具有巨大優勢，主動控制技術[5]是其核心技術中必不可少的一部分。通過主動控制，可以實現性能的多目標優化。多電、全電發動機技術正在起步，美國和歐盟等國家預計，多電航空發動機將在2020年左右投入使用。多電發動機是未來先進航空發動機的發展趨勢，而探索轉子系統的振動主動控制策略是其設計的重要內容。

對于航空發動機轉子系統主動振動控制的研究是近代轉子動力學新興的領域，主要包括3個方面的內容：控制的性能函數，施加主動控制力的方法以及控制器的設計等。Glasgow等[6]對轉子系統的模態控制做了較為詳細的分析，但是由于陀螺力矩的作用，模態隨轉速變化，對于高轉速的航空發動機轉子來講，很難達到快速跟蹤、快速控制的目標。魯棒控制又稱為穩健性控制，可以有效的降低系統某些參數的敏感度，自1981年被Zames[7]提出后，獲得迅速發展[8,9]，并在轉子動力學中得到了較好的應用[10,11]。劉雍等[12]首次將魯棒控制應用于航空發動機轉子系統的減振設計，所設計的H∞控制器不僅提高了系統對剛度參數變化的抗干擾能力，而且可以主動控制其周期擾動，但是由于控制目標和控制器的設計較為單一，對初始結構效率比較惡劣的轉子結構系統，改善其綜合性能依然較為困難。賀爾銘等[13]應用最優控制和極點配置方法，通過調節臨界轉速、阻尼比和不平衡量，實現了航空發動機轉子的綜合控制。上述不同的控制策略，均可實現對轉子振動的主控控制，但是控制策略均比較單一。為了達到更好的抑振效果，本文綜合前述研究經驗，考慮航空發動機轉子系統在初始結構設計較難滿足結構效率要求的前提下，通過主動控制器的綜合設計，實現多目標變量的有效控制，從而提高航空發動機整體力學性能，縮短研制周期，減少費用支出。

航空發動機轉子系統主動振動控制的目的[14]主要有3個：首先，轉子系統在工作轉速鄰域內應具有一定的裕度（工程上一般為20%），即需要合理的配置臨界轉速，減小轉子的振動幅值，從而減小其變形所帶來的氣動效率損失。其次，轉子系統對不平衡量的低敏感性。例如轉子結構的平衡配重是在有限個轉速下進行的，因此在飛行包線內仍存在一定的不平衡響應，這時應保證轉子具有足夠的抗變形能力。最后，轉子系統在結構參數變化范圍內應具有一定的穩健性。由于航空發動機轉子系統大量存在止口、螺栓、端齒和套齒等連接結構，這會導致轉子結構的非連續性，并且由于材料、加工、裝配的差異，以及多變的工作狀態，導致外部載荷的非確定性，這些因素均會使轉子結構的質量/剛度在一定范圍內發生變化。這時應在保證系統穩定的前提下，使受擾后的轉子結構振動響應幅值盡快衰減。

綜上，主動控制力u應包括三項，即u=u_1+u_2+u_3。其中，u_1用于臨界轉速的配置，保證工作轉速下具有足夠的裕度，采用狀態反饋極點配置法；u_2用于控制系統的對不平衡響應的敏感性，采用最優控制方法；u_3用于在小擾動下，快速衰減瞬態響應，采用魯棒控制方法。最終實現轉子系統的控制綜合，以期實現最優或次優控制。航空發動機轉子系統施加主動控制力方法可以通過可控擠壓油膜[15,16]、電磁軸承[17,18]、智能材料[19]等實現，相關文獻有著較為詳細的敘述，在此不做過多說明，僅做相關理論研究。

1 轉子系統動力特性的狀態空間表達

一般具有一定偏心質量的轉子系統渦動微分方程具有如下形式：

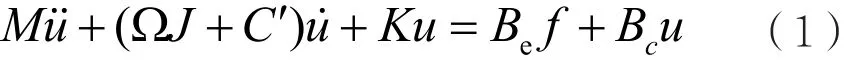
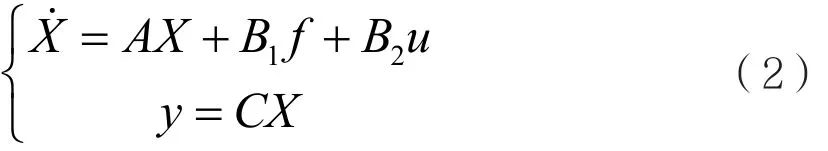
若以調控轉子系統的臨界分布為目標，應使用u1控制。假設零初始狀態，對式（2）左右進行拉氏變換，得到輸出的拉氏變換y( s)為：

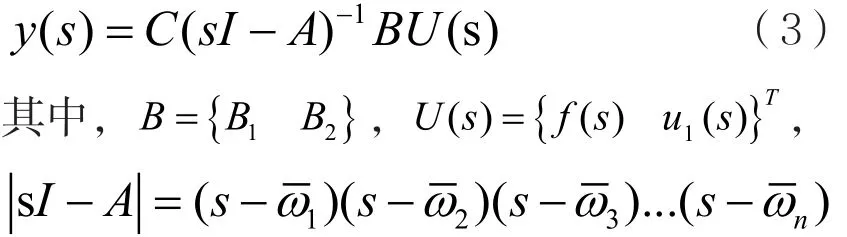
若以降低轉子對不平衡響應的敏感度為目標，應使用u2控制。假設系統在不平衡力的作用下的響應為u0，擾動為ξ，則受擾后系統的響應為： u=u0+ξ，將其代入方程（1），可得擾動的運動狀態微分方程：

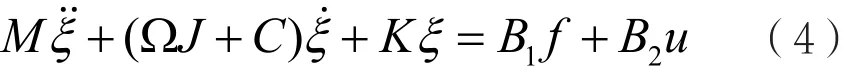
此處u2的作用常常是使系統引入最佳阻尼，進而改變系統的阻尼陣，用于衰減不確定因素引起的瞬態振動。此時，系統的擾動由未受控時變為受控時的（這里ξ為初始擾動，0p為未受控時的特征值，pc為受控時的特征值）。由此可見，u2的引入主要是使受控系統得到所需的模態阻尼。

若以快速衰減瞬態響應為目標，可以使用u3控制。如圖1所示，P( s)和C( s)為別為轉子系統和控制器的傳遞函數，u3、e、d和y分別為外部輸入、誤差信號、外部擾動輸入和控制對象輸出（位移）的測量值。當d=0時，由外部輸入u3到控制對象輸出y的閉環傳遞函數為：

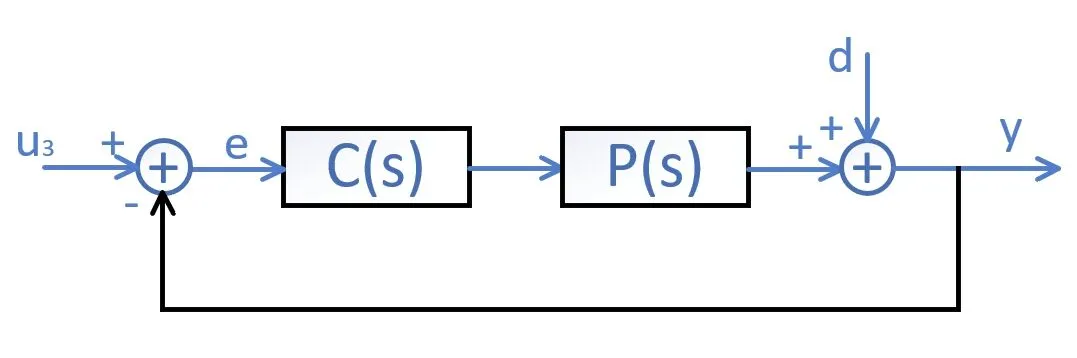
圖1 閉環系統U3控制器示意

TS，現在把P( s)當做變化參數，計算T( s)對P( s)的變化靈敏度，當P( s)變化為 P( s) +ΔP( s)時，T( s)的變化ΔT( s)為：

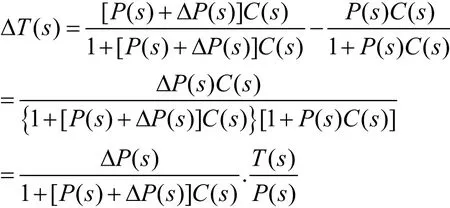
進一步可得：

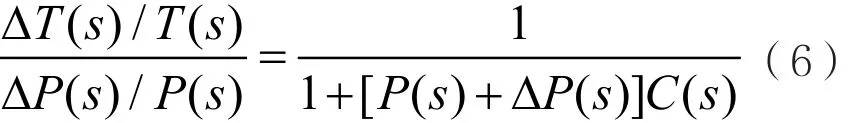
當式（6）中的 Δ P( s) → 0的極限，可求出T( s)對P( s)的變化的靈敏度函數S為

可以看出，式（6）在d=0時是閉環控制系統中由u3到e的傳遞函數，在u3=0時是由d到y的傳遞函數。也就是說，由式（7）描述的靈敏度函數S即描繪了u3對誤差信號e的影響，又反映了外部干擾d對控制對象輸出測量值y的影響。所謂降低系統對外部干擾的敏感性，即是將靈敏度函數的范數降到一個較低的值。

2 控制器設計

本文采用狀態反饋極點配置、最優控制和魯棒控制等現代控制綜合的方法，分別實現對轉子系統的臨界裕度、不平衡量敏感性和瞬態衰減的主動控制。

2.1 u1控制器設計

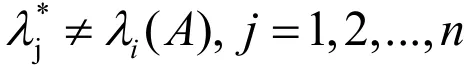
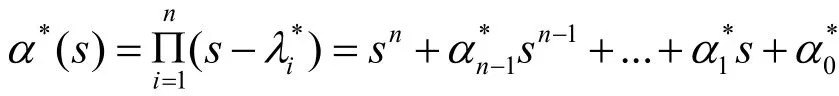
基于此，引入任意n× n非奇異時常陣H，可將矩陣F取為：

步驟4：判斷T的非奇異性。若T非奇異，進入下一步。若T奇異，返回步驟2，即重新選取，重復以上計算過程。

步驟5：計算 T-1，計算所求的狀態反饋矩陣，計算完成。

2.2 u2控制器設計

線性系統的二次型最優控制器設計是現代控制理論最重要的成果之一，在工程上得到了廣泛應用，其最重要的問題是需要選定合適的性能指標函數。性能指標函數一般具有如下形式：

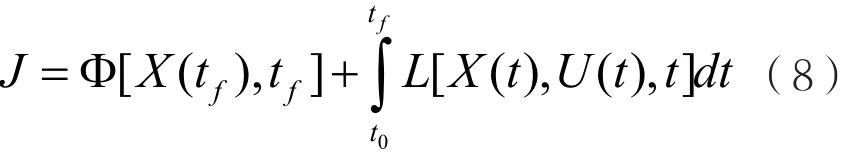
式（8）包括終端指標和積分指標兩部分。在航空發動機轉子系統主控控制中，一般不考慮終端指標。這里不妨取頻率的二次型指標作為性能指標函數，形式如下：

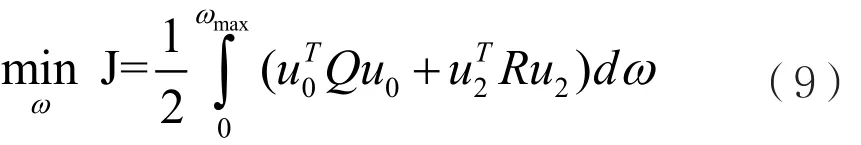
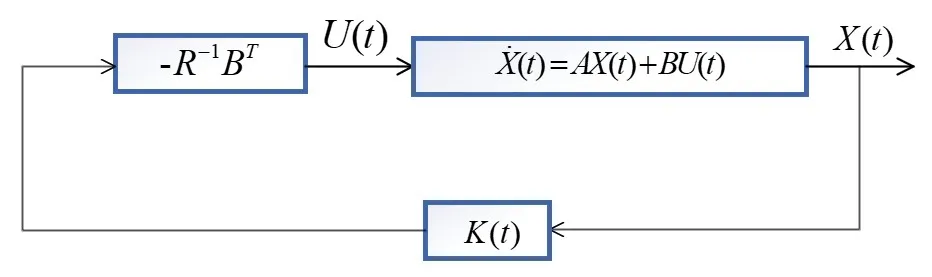
圖2 最優反饋控制系統

其控制器的設計可以可歸結為求解非線性黎卡提矩陣微分方程或代數方程。

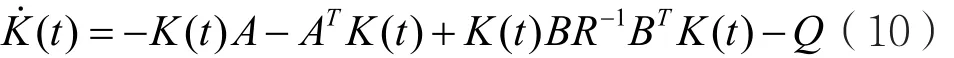
式（10）是K( t)的矩陣微分方程。

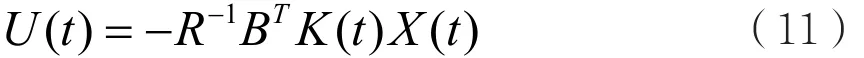
K( t)與X( t)無關，所以可在運行前將R-1BTK( t )離線計算出來，并存儲于計算機中。在系統運行時，將 -R-1BTK( t )從存儲中取出，與同一時刻測量到的X( t)相乘，構成最優控制U( t)。所以系統運行時的計算量只含一個乘法計算，計算量很小。至于黎卡提矩陣方程的求解早已得到廣泛深入的研究[20]，有標準的計算機程序可供使用，求解規范方便。

2.3 u3控制器

控制系統魯棒性分析的主要內容是控制分析系統在一組不確定性作用下的穩定性、穩態性能和動態性能，可歸結為魯棒穩定性分析和魯棒性能分析這兩個方面。在航空發動機轉子結構設計中，魯棒控制器的存在條件能夠提供構型不確定性和外部干擾不確定性的范圍，這便是魯棒控制器的實際應用。

形如狀態空間表達，若采用魯棒H∞控制，可以寫成如下的形式：

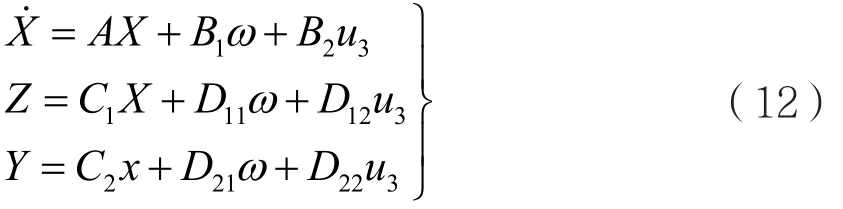
w為外部輸入信號，u3是控制輸入信號，Z是可控輸出信號，Y是可觀輸出信號，要求(A , B2)能控，(C2,A )能觀。對式進行拉氏變換，可得傳遞函數矩陣與狀態方程之間的關系，即

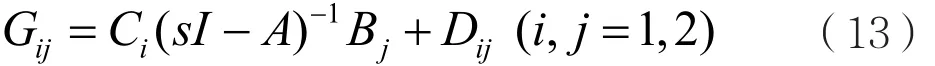
由此可得干擾輸入w到可控輸出y之間的傳遞函數為：

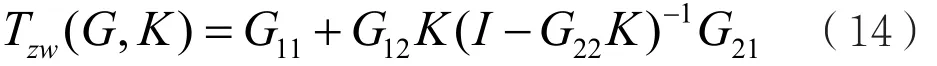
H∞標準控制問題（如圖3所示）之一就是通過設計控制器K( s)使閉環控制系統穩定且傳遞函數的無窮范數滿足：

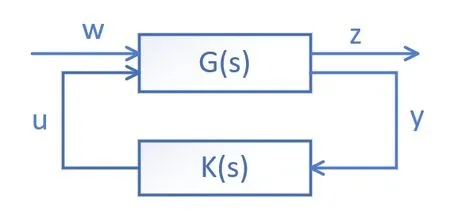
圖3 H∞ 標準反饋控制系統

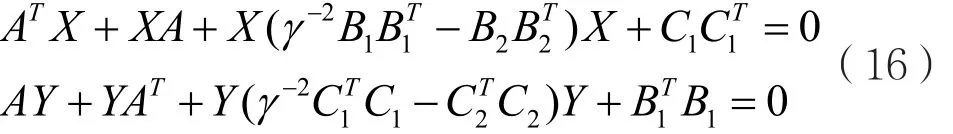
當然，在進行H∞控制器的設計時，首先應檢查H∞控制器是否存在，否則因某些條件不滿足，不能設計出所需的控制器。

2.4 綜合控制器

圖4 綜合控制器示意圖

圖4中的u1控制器K是靜態的，與時間無關。因此可以在施加u1控制系統（圖中紅色虛線框內）的基礎上選擇施加u2控制器或u3控制器，具體需要施加u2（最優控制）還是u3（魯棒控制）需要根據實際控制目標確定。

3 綜合控制仿真分析

為了證明本文提出的綜合反饋動態控制器的抑振效果，對轉子-支承系統進行綜合控制仿真分析。考慮到實際轉子的復雜性和主動控制方法的通用性，采用如圖5所示的航空發動機轉子-支承系統簡化模型[21]，這里只給出轉子變形在xoz面上的投影，yoz面與之相同。

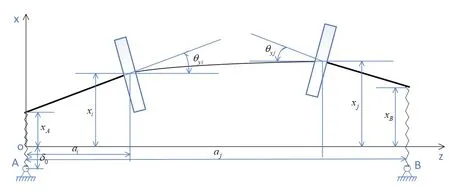
圖5 轉子變形在xoz平面上的投影

先分析轉子圓盤與彈性支承的速度和位移，計算轉子的動能和勢能，進而采用Lagrange方程建立彈性支承偏置轉子系統的穩態渦動微分方程。設xi、θyi，yi，θxi分別為第i個圓盤形心在oxz平面內和oyz平面內的絕對位移與轉角，xA、xB和yA、yB分別為兩端支承A和B在oxz平面內和oyz平面內的位移。忽略軸向變形與扭轉變形的影響，穩態渦動時N個圓盤與兩個彈性支承共有4N+4個自由度。選取廣義坐標為

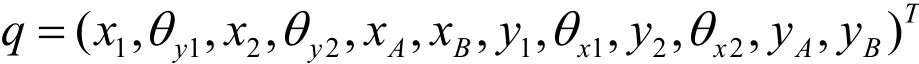
系統的動能T為支撐動能Tb與圓盤動能Td之和：

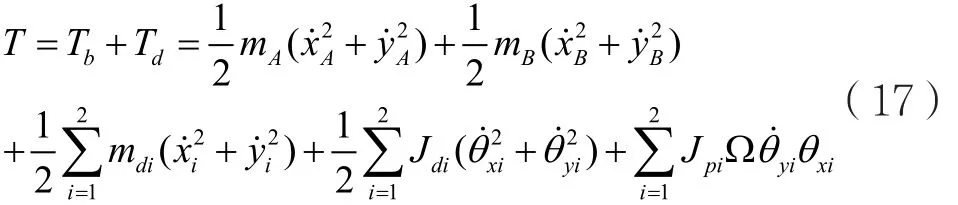
在xoz面的任意瞬時，根據兩端彈性支承位移引起的第i個圓盤形心位移和截面轉角與兩端支承位移的幾何關系為：

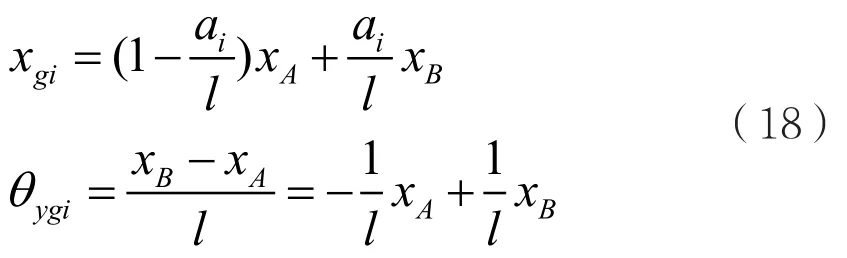
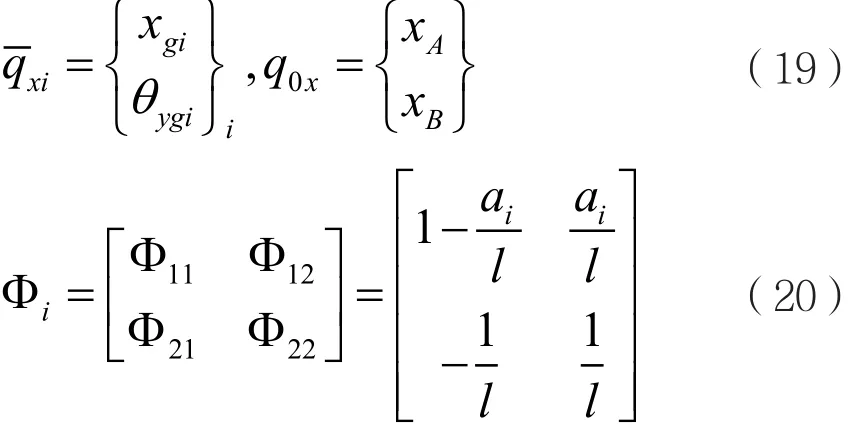
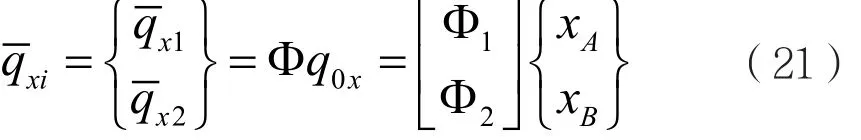
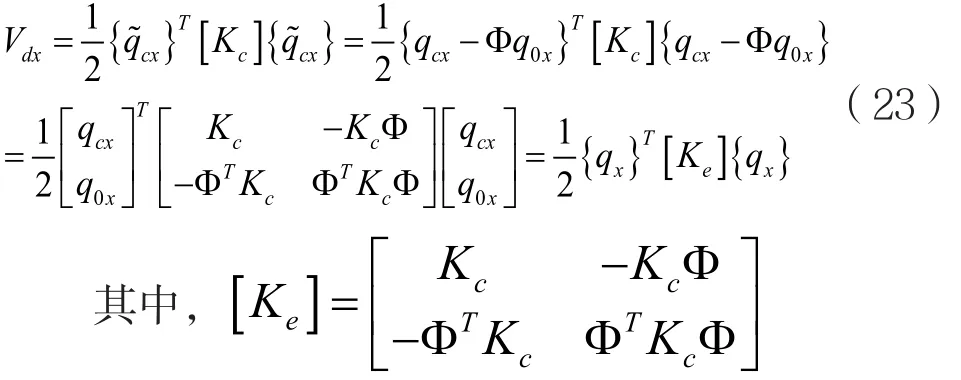
整個轉軸的彈性勢能應是oxz面內的彈性勢能和oyz面內彈性勢能的疊加：

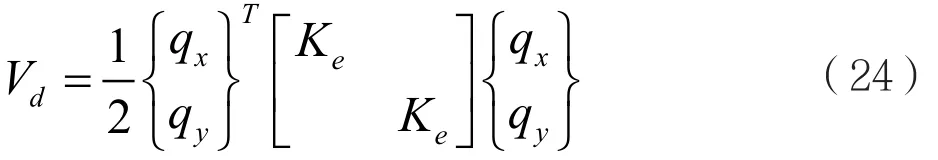
兩端彈性支承的動能：

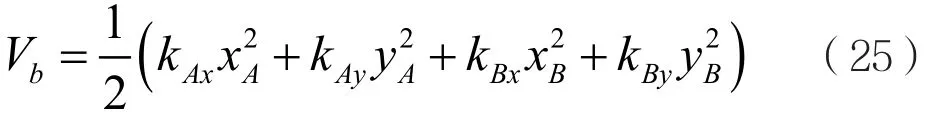
轉子系統的總動能：

設各圓盤的偏心距為 ei(i=1,2)，根據廣義力定義可得：

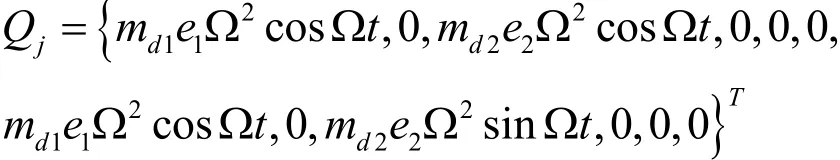
將動能和勢能的表達式帶入拉格朗日方程：

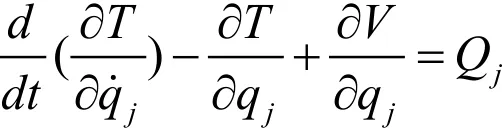
由此可以得到兩端彈性支承單跨多盤轉子系統的渦動微分方程：

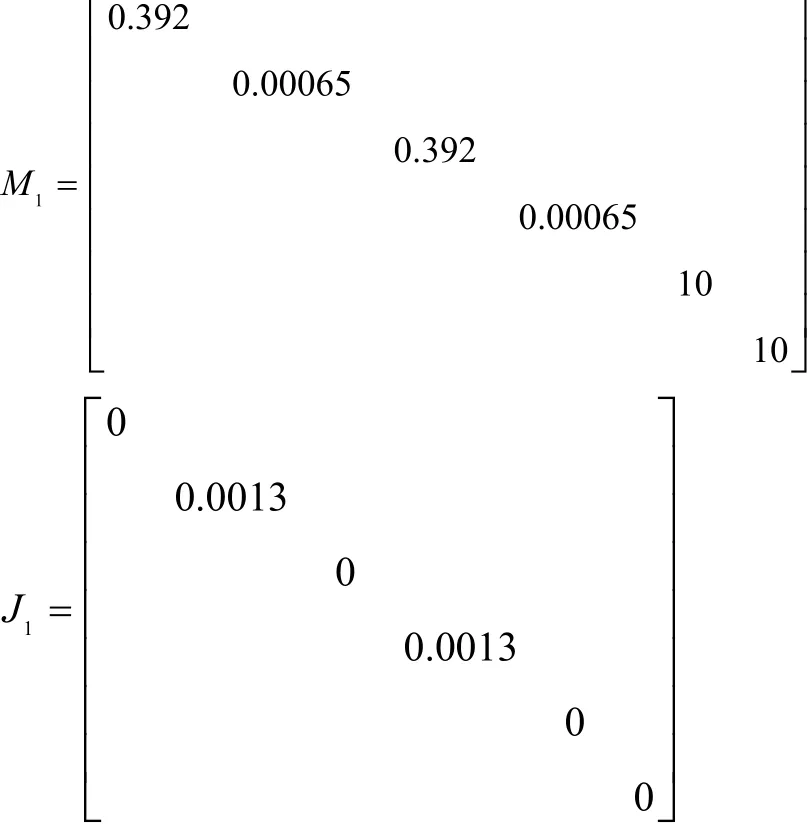
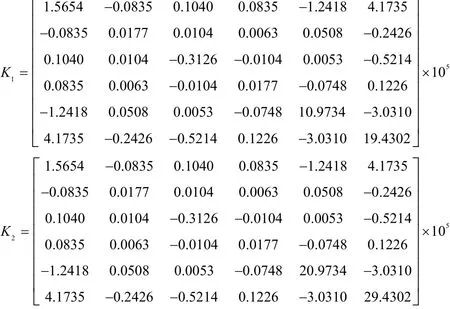
所得到轉子的坎貝爾圖如圖6、圖7所示，當轉子從0轉速加速到14000 rpm時，將經過2階臨界轉速（只考慮不平衡量激起的正進動），共振轉速分別為3480 rpm，11847 rpm。

假如轉子系統工作在11850 rpm附近，則可能會因為工作轉速與共振頻率之間的裕度過小而容易發生共振。假如規定需要將轉子的2階共振轉速降到11000 rpm以下，則可以通過u1控制器實現。首先應通過線性變換提取原系統可控的部分，并考慮只能在軸承位置施加主動力，可設定常控制器為：

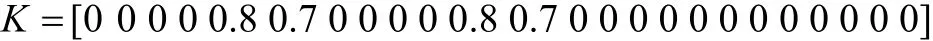
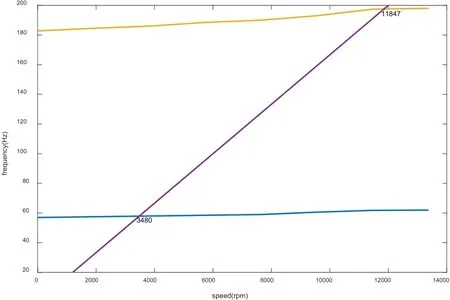
圖6 坎貝爾圖（控制前）

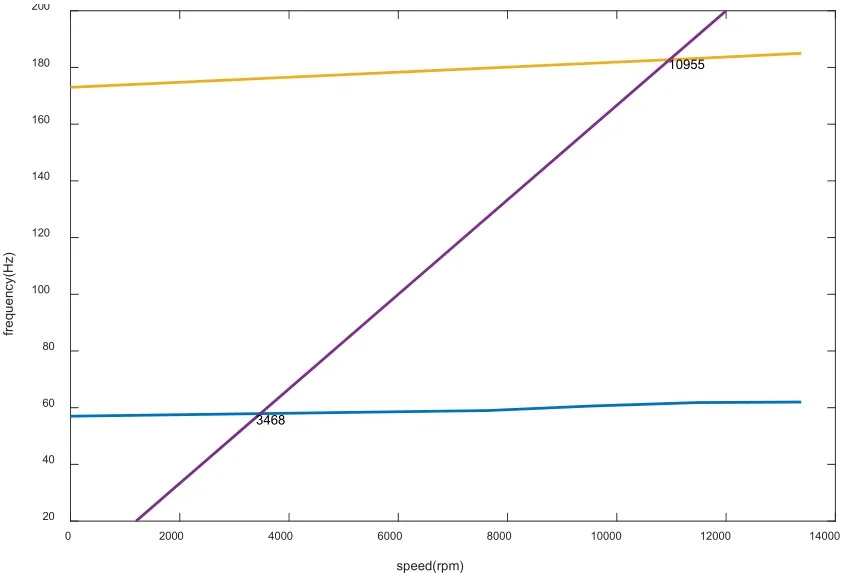
圖7 坎貝爾圖（控制后）

假設轉子在盤1上存在不平衡量6g· mm，此時方程存在右端項：

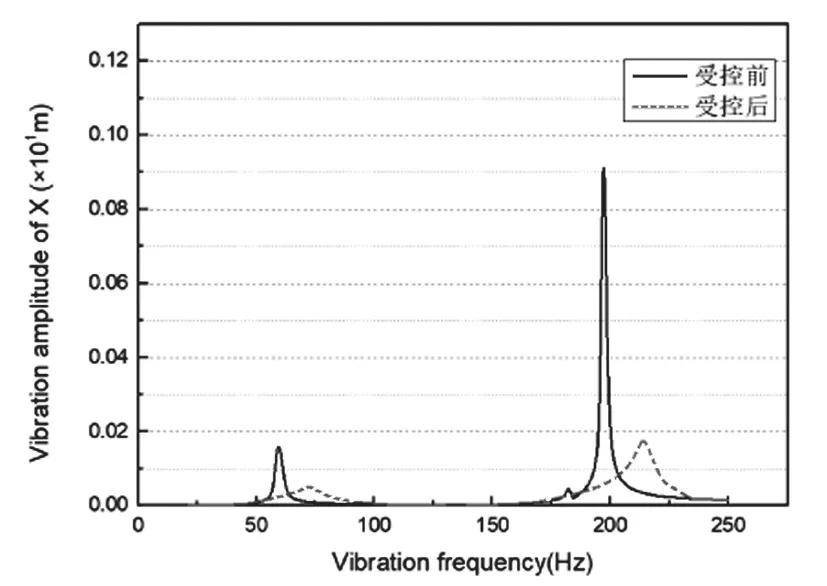
圖8 X方向控制前后振幅

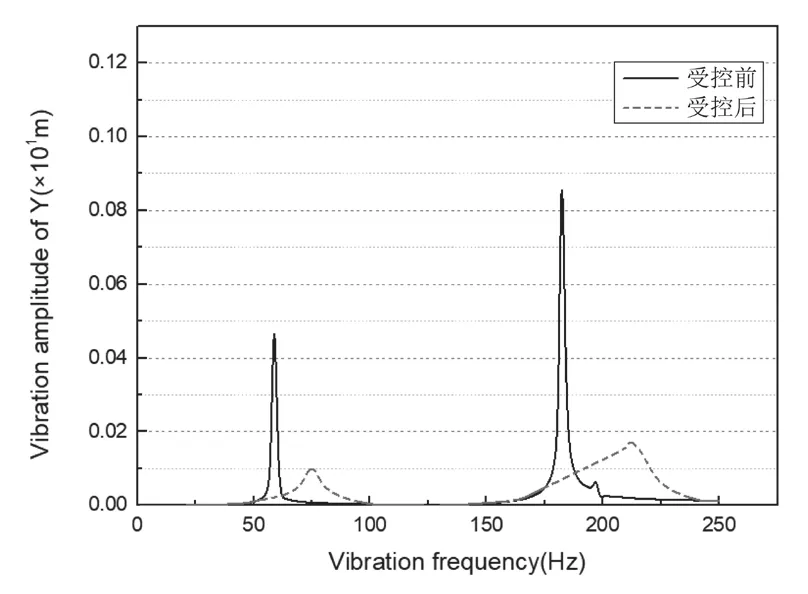
圖9 Y方向控制前后振幅

由圖8和圖9可看出，施加主動控制力后的振動幅值（圖中虛線）相比于轉子的原始狀態，不平衡力引起的振動幅值大幅度減小。

u3控制器的控制效果與u2類似，為節省篇幅，不再論述。值得說明的是，在實際應用中由于航空發動機轉子結構復雜，難以寫出具體表達式，這時可以采用商用有限元軟件提取轉子結構的質量、剛度等矩陣，并采用動態數值仿真，實現轉子振動的主動控制。由于計算量很大，本文以簡單轉子為例，僅為說明航空發動機轉子系統主動抑振技術的可行性。

4 結論

通過系統的極點配置可以有效的改變轉子系統臨界轉速的分布。由于反饋矩陣為常矩陣，不受時間的影響，因此反饋后的控制系統可以作為一個優化的新系統，可以由優化系統的結構特征參數指導原結構的優化和改進，以期實現轉子結構與力學特征的一體化設計，為航空發動機轉子結構設計提供指導。當考慮轉子結構系統因連接界面等非確定因素的影響時，實時追蹤的反饋系統控制仍有待進一步探索。

通過航空發動機轉子系統主動抑振綜合控制，可以有效降低轉子的不平衡響應，大幅提高轉子系統的可靠性和安全性。同時，通過主動控制綜合策略，可以在結構構型布局比較不合理的前提下進行相關力學特征的控制，從而整體提升其力學性能。

航空發動機轉子系統主動控制綜合策略仍有待需完善之處，如在控制過程中如何快速準確的跟蹤到轉子系統故障所引起的力學特征參數的變化，進而快速準確的選取響應的控制策略。