含參數“二次型”不等式恒成立問題的解法

江西省贛州市寧都中學 陳珊珊

二次函數是高中數學知識板塊的重要組成部分，也是高考考查的一大熱點。命題時多與其他知識交匯融合，特別是含參類不等式問題，一直是高考重點考查的題型。此類問題的求解常常需結合數形結合、分類討論、化歸與轉化等思想方法，是高考的一大難點。“二次型”不等式恒成立問題一般都要轉化為求函數的最值問題。下面從三個方面來介紹含參數的“二次型”不等式的解法。

一、判別式法

分析：解決此類問題的常規思路是，先對不等式的二次項系數a進行分類。當a=0時，是一元一次不等式；當a≠0時，是一元二次不等式。

解：（1）當a=0時，原不等式等價于-x-1≤0，解得x≥-1，此時不合題意，舍去；

評析：若所給變量x的取值范圍為全體實數R，一般先對不等式中的參數進行分類：若轉化為一次不等式，則肯定不滿足；若是二次不等式，則依據開口方向和判別式同時判定，列出需要滿足的條件，解不等式即可。

二、分離參數法

如果含參數的不等式中的參數和其余變量容易分離，那么常用方法是將參數放于不等式一邊，其余變量整體放于不等式另一邊，然后再研究含有其余變量的式子對應函數的最值，以此求得參數的取值范圍。

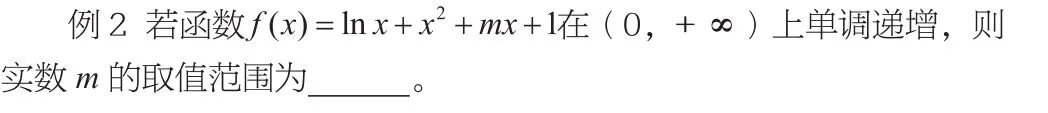
三、變換主元，構造新函數法

在很多的含參數二次不等式問題中，特別是當參數最高次是一次時，我們通常將函數變量字母與參數字母“地位”對調，將式子變形為以參數為新變量的不等式，將二次函數不等式轉化為一次函數不等式來求解。

分析：這個不等式已知的是參數m的取值范圍，反而是求“常規變量”x的取值范圍，我們可以將不等式轉化為關于m的“一次型”函數。那么把原來關于x的不等式恒成立問題等價轉化為關于新變量m的一次不等式恒成立問題，則只需滿足端點對應的函數值恒小于0。

從以上解法可以看出，一般含參類不等式恒成立問題的處理方法大都可以轉化為函數的最值問題，這也是我們處理這類問題的常規思路。本文僅介紹了判別式法、分離參數法和變換主元，構造新函數法三種解答方法。實際上，另外還有數形結合法、函數性質法、整體代換法、反證法等多種解法，需要大家在平時的學習和練習中多歸納、多總結。