實(shí)施有效教學(xué)提升新授課的課堂效率
侍書(shū)麗
(江蘇省蘇州國(guó)際外語(yǔ)學(xué)校 213151)
有效教學(xué)是老師們一直關(guān)注的問(wèn)題,教學(xué)設(shè)計(jì)不只是關(guān)注知識(shí)的傳授,更應(yīng)關(guān)注學(xué)生的學(xué)習(xí)過(guò)程和情感體驗(yàn)過(guò)程,滿足新的情境和學(xué)生新的需求,所以設(shè)計(jì)要有延伸的空間,要讓學(xué)生不僅形成知識(shí),還要形成對(duì)知識(shí)的進(jìn)一步探索,才能真正達(dá)到“高效課堂”的目的.
啟發(fā)式教學(xué)是歷久彌新的話題,能激發(fā)學(xué)生的求知欲,使新授課教學(xué)變得靈動(dòng)高效.啟發(fā)式教學(xué)的關(guān)鍵在于教師延遲判斷.以下是我的一點(diǎn)嘗試.
一、創(chuàng)設(shè)啟發(fā)性的教學(xué)情境,引發(fā)學(xué)生內(nèi)在的學(xué)習(xí)需求
教學(xué)情境是指在課堂教學(xué)中,根據(jù)教學(xué)內(nèi)容,為教學(xué)目標(biāo)所設(shè)定的,適合學(xué)習(xí)主體并作用于學(xué)習(xí)主體,產(chǎn)生一定情感反應(yīng),能夠使其主動(dòng)積極地建構(gòu)性學(xué)習(xí)的具有學(xué)習(xí)背景、景象和學(xué)習(xí)活動(dòng)條件的學(xué)習(xí)環(huán)境.它可以貫穿于全課,也可以是課的開(kāi)始、課的中間或課的結(jié)束.
案例一《補(bǔ)角、余角》這節(jié)內(nèi)容,有老師精心設(shè)計(jì)了一副三角板的不同擺放:

這樣的情境導(dǎo)入有兩個(gè)優(yōu)點(diǎn):一學(xué)生對(duì)它“熟”,二是直觀,一目了然.不過(guò),如何讓它發(fā)揮更大的作用呢?這就需要我們深入一點(diǎn)去思考.如果老師讓學(xué)生拿起自己的一副三角板擺擺,讓學(xué)生體驗(yàn)一個(gè)三角板不動(dòng),另一個(gè)三角板輕微轉(zhuǎn)動(dòng),觀察∠1與∠2的關(guān)系是否改變.這時(shí)一定會(huì)有學(xué)生想大幅度轉(zhuǎn)動(dòng)三角板的沖動(dòng),三角板重疊的情況,其實(shí)正是老師精心設(shè)計(jì)的例題.但若有這樣一個(gè)活動(dòng)體驗(yàn),學(xué)生還可能會(huì)腦洞大開(kāi),移動(dòng)甚至拉開(kāi)尺子,這時(shí)就會(huì)發(fā)現(xiàn)任意移動(dòng)和平行移動(dòng)的區(qū)別……這樣的活動(dòng)可貫穿于全課.
案例二講《二次函數(shù)》章頭課時(shí),老師們最喜歡出示一幅又一幅圖片,如學(xué)生打籃球、跳繩、拱橋、隧道等,老師們?yōu)榱宋龑W(xué)生,引起興趣,還會(huì)專門拍自己班級(jí)同學(xué)打籃球的情景,學(xué)生面對(duì)圖片應(yīng)接不暇,走馬觀花,這樣的開(kāi)場(chǎng)能維持學(xué)生多久的興趣呢?圖片沒(méi)了,興趣也隨之消退了.因?yàn)槎魏瘮?shù)的圖象是拋物線,我們不妨就出示打籃球的情景,并放慢鏡頭,越慢越好,讓學(xué)生看著球從拋出到落下形成的路徑,并形成猜想:是弧嗎?還是不為我知的一種特殊路徑?學(xué)生自然形成思考,聯(lián)想物理學(xué)的知識(shí),有的學(xué)生應(yīng)該能知道不可能豎直落下,這種特殊路徑有什么特征嗎?學(xué)生在經(jīng)歷觀察、猜測(cè)、推理等活動(dòng)過(guò)程之后,必然引起無(wú)限的遐想和對(duì)新知識(shí)的渴望.
以上的兩個(gè)案例都是概念教學(xué),知識(shí)點(diǎn)簡(jiǎn)單,老師們往往覺(jué)得沒(méi)什么東西可挖,便錯(cuò)誤地以為有個(gè)情境引出概念就行,忽視了思維的深入訓(xùn)練,使啟發(fā)式情境導(dǎo)入得不到落實(shí).
二、創(chuàng)設(shè)啟發(fā)性的數(shù)學(xué)教學(xué)過(guò)程,激發(fā)學(xué)生內(nèi)在的學(xué)習(xí)需求
新授課的知識(shí)生成之后,例題如何教學(xué)呢,老師們的差異還是很大的.常用的啟發(fā)式教學(xué)手段有一題多解、一題多變、設(shè)計(jì)問(wèn)題串等,這里我主要從設(shè)計(jì)問(wèn)題上舉兩個(gè)案例.
案例三問(wèn)題的實(shí)質(zhì)呈現(xiàn):
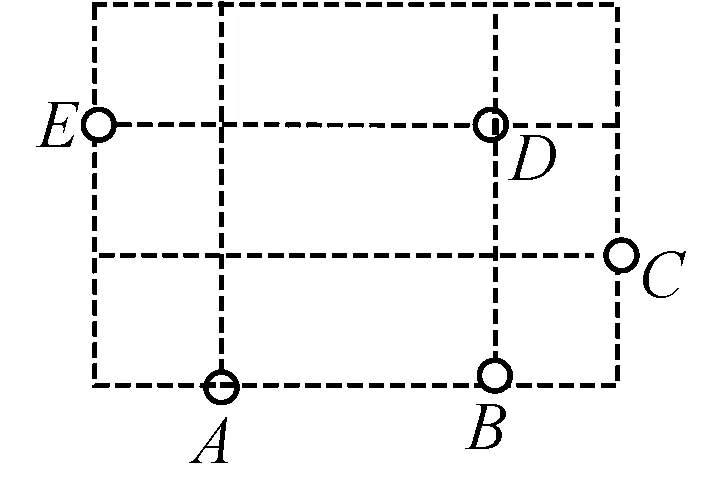
如圖過(guò)A、B、C、D、E、五個(gè)點(diǎn)中任意三點(diǎn)畫(huà)三角形:
(1)其中以AB為一邊可以畫(huà)____個(gè)三角形;
(2)其中以點(diǎn)C為頂點(diǎn)可以畫(huà)____個(gè)三角形;
(3)過(guò)其中任意三點(diǎn),一共可以畫(huà)____個(gè)三角形.
不妨將本題講解做如下設(shè)計(jì):
先留5分鐘左右的時(shí)間獨(dú)立完成,然后逐一提問(wèn),學(xué)生答完后,老師提出:第(3)問(wèn)是怎么求出來(lái)的呢?這時(shí)一定有不少學(xué)生是計(jì)數(shù)出來(lái)的.此時(shí)老師再提出:若第(3)問(wèn)給出符合條件的點(diǎn)是15個(gè)呢?這樣的設(shè)問(wèn),讓學(xué)生的認(rèn)知和情感處于“欲知還未知,欲言還未能”的困惑狀態(tài),啟發(fā)學(xué)生對(duì)原先的認(rèn)知發(fā)生沖突,進(jìn)而尋求出揭示問(wèn)題本質(zhì)的解法:
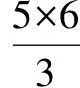
案例四突破難點(diǎn)的問(wèn)題鋪設(shè)

(1)試探究當(dāng)m分別為1、2、3時(shí)這個(gè)分式方程的解的情況;(2)若這個(gè)分式方程無(wú)解,試求m的值.
第(1)問(wèn)的設(shè)計(jì)至關(guān)重要,甚為巧妙,為后面的問(wèn)題直接鋪好了路,使后面的問(wèn)題明朗化,簡(jiǎn)單化,但需要注意的是,這種使問(wèn)題簡(jiǎn)單化并不是沒(méi)有思考,數(shù)學(xué)中有一種思想叫“由特殊到一般”,在做完第(1)問(wèn)之后,是需要悟出第(2)問(wèn)的一般情況的,而且這是一種逆向思維,不是所有的學(xué)生都能順利通過(guò)的.做完這題之后,學(xué)生還能體會(huì)出不含字母的分式方程按一般步驟解下去,最后只需檢驗(yàn)即可,但含字母的分式方程,變形的每一步都可能因?yàn)樽帜溉≈挡煌a(chǎn)生各種情況,再做其他類含字母的問(wèn)題時(shí),他們都會(huì)小心翼翼地邁出每一步,這是培養(yǎng)他們良好的學(xué)習(xí)習(xí)慣的途徑之一.
案例五整體思想的滲透
在同學(xué)們已掌握二元一次方程組的解法基礎(chǔ)上,設(shè)計(jì)了這樣一道例題:
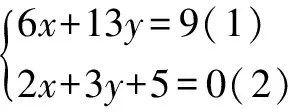
基本方法是代入消元法和加減消元法,但老師提出是否有更合適的方法求解呢?學(xué)生便形成了思考,進(jìn)而形成了本節(jié)課新的生長(zhǎng)點(diǎn)——運(yùn)用整體思想.但這個(gè)整體是誰(shuí)?也會(huì)引起學(xué)生思維的碰撞乃至升華!法一:大多數(shù)學(xué)生能想到的是2x=-3y-5整體代入;法二:少數(shù)人會(huì)大膽超越,把2x+3y=-5整體代入;既然如此,當(dāng)然會(huì)有更大膽的把2x+3y+5=0整體代入.
數(shù)學(xué)思想是從數(shù)學(xué)知識(shí)中提煉出來(lái)的數(shù)學(xué)學(xué)科的精髓,是將數(shù)學(xué)知識(shí)轉(zhuǎn)化為數(shù)學(xué)能力的橋梁,因此在數(shù)學(xué)教學(xué)中要不斷滲透各類思想,讓學(xué)生體驗(yàn)其辯證性及規(guī)律性的魅力,這個(gè)案例不僅讓整體思想“活”了起來(lái),也讓學(xué)生的思維活了起來(lái),讓學(xué)生理解了它的精髓所在,更使他們?cè)谝院蟮膶W(xué)習(xí)中能靈活的運(yùn)用,才能實(shí)現(xiàn)新課標(biāo)指出的:“數(shù)學(xué)教育既要使學(xué)生掌握現(xiàn)代生活和學(xué)習(xí)中所需要的數(shù)學(xué)知識(shí)與技能,更要發(fā)揮數(shù)學(xué)在培養(yǎng)人的思維能力和創(chuàng)新能力方面的不可替代的作用.”
以上只是從新授課的情境引入和例題講解兩個(gè)側(cè)面簡(jiǎn)單闡述了啟發(fā)式教學(xué)的應(yīng)用以及問(wèn)題設(shè)計(jì)中老師留有的余地,這份留白便是數(shù)學(xué)教學(xué)中最閃亮的特征,我們的課堂是有生命體的課堂,不能靠機(jī)械的反復(fù)訓(xùn)練獲取知識(shí),只有賦予他們一個(gè)生動(dòng)活潑的、主動(dòng)的和富有個(gè)性的過(guò)程,才能認(rèn)真聽(tīng)講、積極思考和自主探索.我相信新授課課堂上老師的刻意留白一定是極佳的、不可替代的教學(xué)方式,是學(xué)生學(xué)習(xí)的主戰(zhàn)場(chǎng),久而久之,就能做到“見(jiàn)樹(shù)木,更見(jiàn)森林”.

