最優單循環賽程編程思路及MATLAB實現

謝曉敏

（川北幼兒師范高等專科學校 初等教育系，四川 廣元 628017）

n支球隊在同一場地上進行單循環比賽，為了保證公平性，按照文獻[1，2]的編排方法，推廣其結論可得：n(n≥5)為奇數時，每兩場相隔場次數為；n(n≥5)為偶數時，相隔場次數為[3]

當球隊數目較少時，可以手工編排賽程，而球隊數目較多時，手工編排就會耗時費力。若能將編排方法用程序實現，就會省時又省力。

筆者將參賽隊數目分為奇數和偶數分別進行討論，理清編程思路，用MTLAB編程給出賽程編排表，并計算出每個參賽隊參加的場次數和每兩場相隔場次數以及總場次和。

一、參賽隊數目為奇數

（一）構造推理法

1.構造推理編排法簡述

單循環賽中每兩個隊伍都要進行一場比賽。對于1號參賽隊而言，它要和其余的隊伍進行（n-1）場比賽，按照 1-2，1-3，…,1-n的順序安排（n-1）輪的第一場比賽。最后一輪只安排一場比賽，其余每輪場比賽。從第1輪到第（n-2）輪的最后一場比賽分別為：2-n,2-3,2-4，…，2-（n-1）。剩余的比賽平均的插入第 1輪至第（n-2）輪，每輪場。使每個球隊的間隔場次數達到。

2.編程思路

（1）將賽程編排表儲存在矩陣A中，當參賽隊有n個時，矩陣A有行，2(n-1)列。第1列與第2列同行的參賽隊進行一場比賽，自上而下形成第一輪賽程安排。第3列與第4列，以此類推，第(2n-3)列與第2(n-1)構成的第(n-1)輪只有一場比賽。矩陣A的初始值為零矩陣。

（2）安排每輪的第一場比賽，即矩陣A的第一行。奇數列為1號參賽隊，偶數列從2號隊遞增到n號隊。再安排每輪的最后一場比賽，即矩陣A的最后一行。為了后面計算間隔方便，最后一行的第1列為2，第二列為n號參賽隊，其余奇數列從3號隊遞增到(n-1)號隊，偶數列為2號參賽隊。后面的安排中只安排第1至第(n-2)輪的比賽。

（5）其余未安排的位置都是最大號參賽隊。

3.MATLAB程序

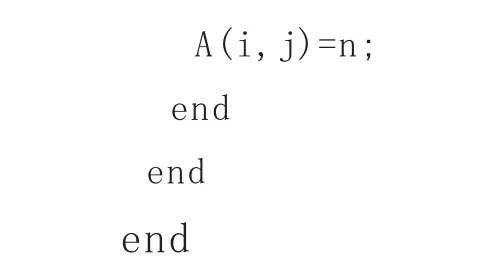
4.賽程安排

將上面的程序保存為gztlf.m文件。在命令窗口輸入〉〉A=gztlf(21)，運行程序，根據程序結果得n=21時的賽程安排如下：

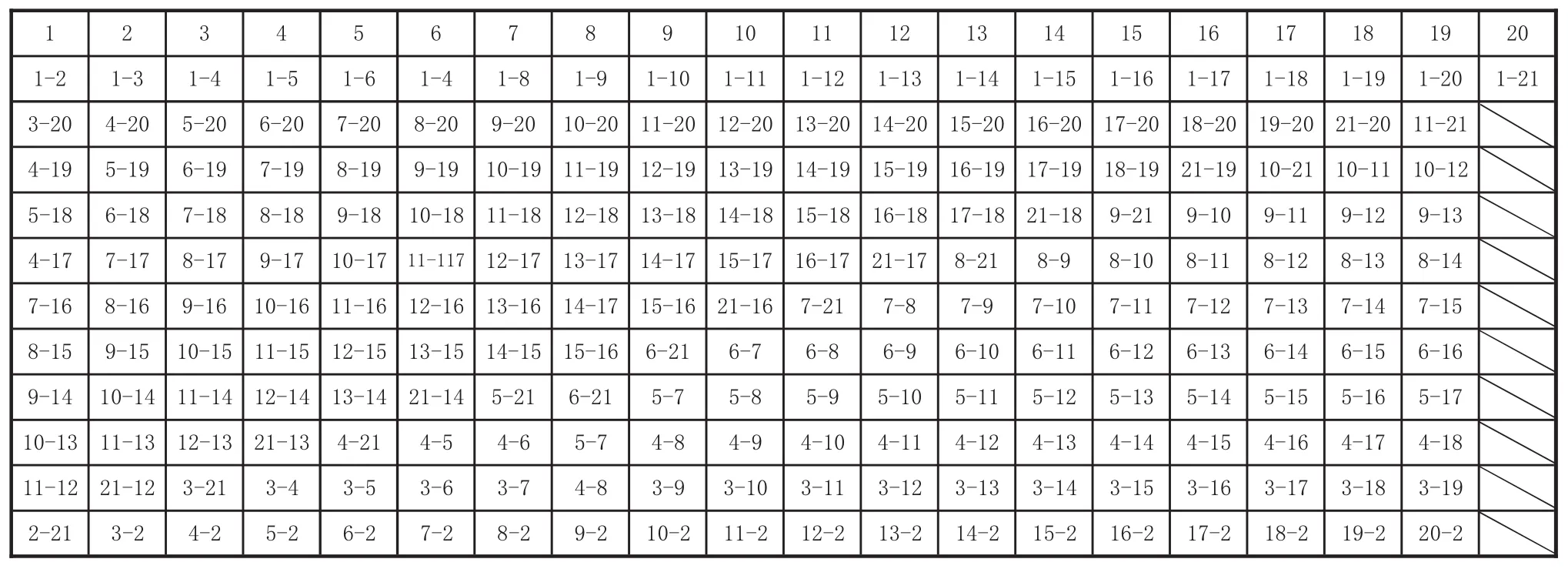
表1 n=21的構造推理法賽程安排

（二）圖論法

1.圖論編排法簡述

將n支球隊代表的點按順時針方向排列成一個“圈”[4]，每兩個點之間連一條線，就形成了一個無向完全圖Kn，n支球隊的單循環賽對應于此圖Kn，Kn有條邊，對應n支球隊的場比賽。將場比賽分成輪，每輪n場比賽。每輪的編排方法基本類似。

首先確定奇數個參賽隊中不參加比賽的隊伍，可以是任意一個隊伍。每輪首先不參加比賽的隊伍必須為同一個隊伍。剩余隊伍數目為偶數個，以不參賽隊所處點為參照點，安排分別從順、逆時針方向看，處在“圈”上對稱位置的兩個隊伍完成一場比賽，按照由近及遠的順序，每隊只能參加一場比賽。共計場比賽。

然后從未參加比賽的隊伍代表的點走到每輪第一場比賽中的隊伍，按照先向小號走再向大號走的原則，為第場比賽。沿每輪第一場比賽的路徑行走，走完后向每輪第二場比賽中的隊伍行走，仍然先向小號走再向大號走，增加一條路徑，每增加一條路徑則安排一場比賽。如此反復，直到走到每輪第場比賽號數較大的頂點，共安排場比賽。從剛才結束的頂點走到起始未參加比賽的隊伍所處頂點，再安排一場比賽，即第n場比賽。

2.編程思路

（1）將賽程編排表儲存在矩陣A中，當參賽隊有n個時，矩陣A有n行，(n-1)列。第1列與第2列同行的參賽隊進行一場比賽，自上而下形成第一輪賽程安排。第3列與第4列，以此類推，第(n-2)列與第(n-1)列形成第輪比賽。

（2）規定：每輪起始未參加比賽的隊伍是號數最大的隊伍。第行奇數列的參賽隊從1依次增加到。偶數列的參賽隊為n。第n行奇數列參賽隊為n,偶數列參賽隊從依次增加到(n-1)。

3.MATLAB程序

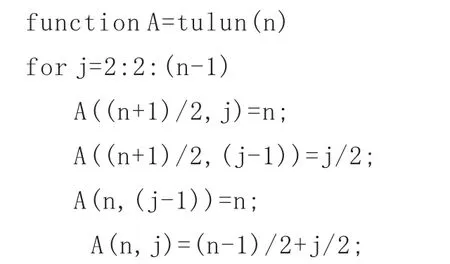
4.賽程安排

將上面的程序保存為tulun.m文件。在命令窗口輸入〉〉A=tulun(21)，運行程序，根據運行結果得n=21時的賽程安排如下：

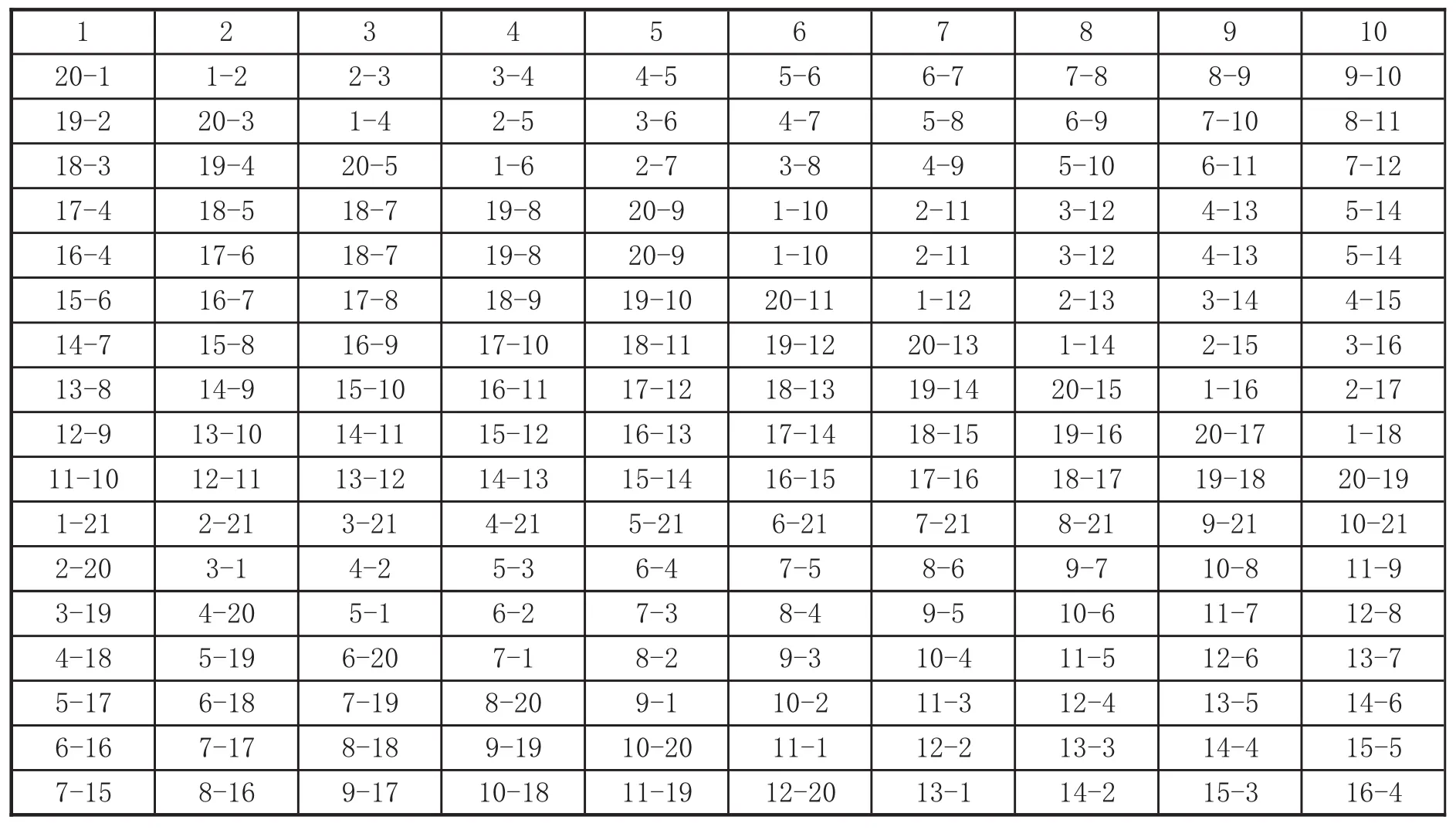
表2 n=21的圖論法賽程安排

表2 n=21的圖論法賽程安排（續）

二、參賽隊數目為偶數

（一）改進的貝格爾編排法簡述

著名的貝格爾編排法[5]編排的賽程共有n-1輪，第一輪按照1至n的順序逆時針按U形走向分成均等兩邊。n號隊安排在每輪的第一場比賽中，第一輪在右邊，第二輪在左邊，第三輪回到右邊，如此反復，第n-1輪又回到右邊。從第二輪起，將前一輪右下角的參賽隊伍提到本輪第一場比賽中來，其余參賽隊伍按照逆時針輪轉。貝格爾編排法不能達到最優的場次間隔。

改進的貝格爾編排法從第二輪起，將前一輪第二場比賽右邊的參賽隊提到本輪第一場比賽中來，其余的隊伍編排方法不變。

（二)編程思路

1.將賽程編排表儲存在矩陣A中，當參賽隊有n個時，矩陣A有行，2(n-1)列。第1列與第2列同行的參賽隊進行一場比賽，自上而下形成第一輪賽程安排。第3列與第4列，以此類推，第(2n-3)列與第2(n-1)列構成第(n-1)輪賽程安排。

2.安排每輪的第一場比賽，即矩陣A的第一行。第 2，3，6，7，…,2(n-1)列，均為 n 號參賽隊，第1列為1號參賽隊，其余列按照從左到右的順序，參賽隊從(n-1)至2的順序依次遞減。

（三）MATLAB程序

（四）賽程安排

將上面的程序保存為gjb.m文件。在命令窗口輸入〉〉A=gjb(20)，運行程序，根據運行結果得n=20時的賽程安排如下：

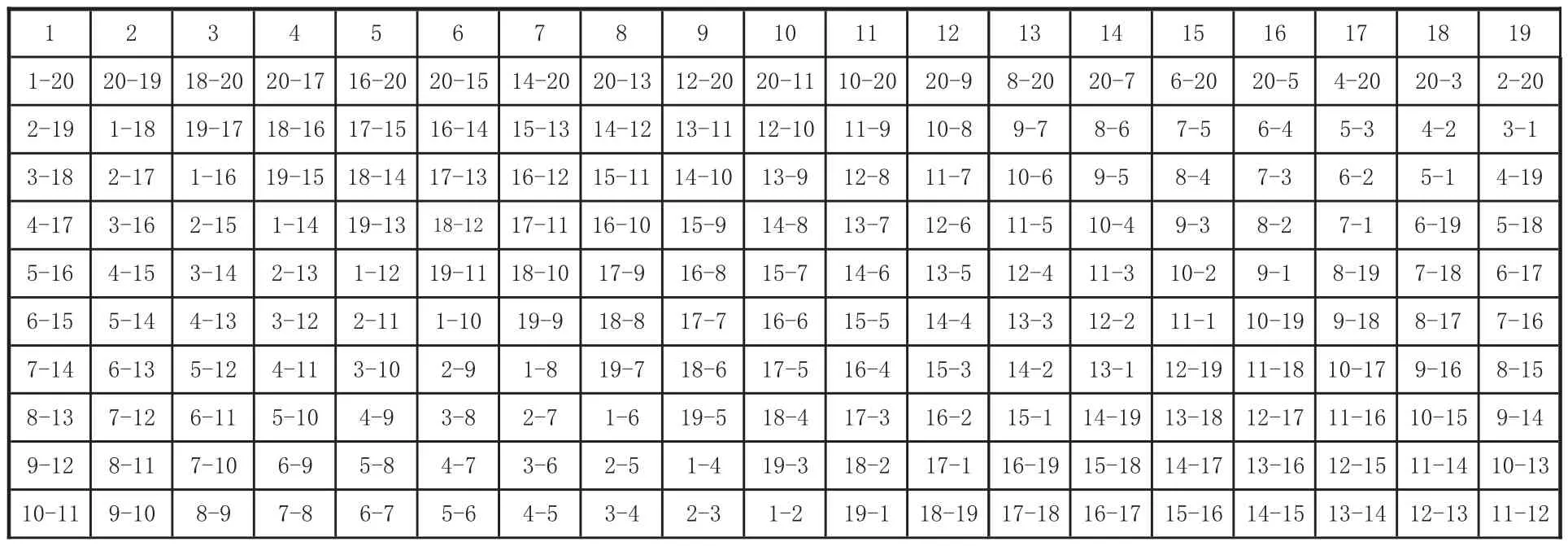
表3 n=20的改進貝格爾編排法賽程安排

三、每個參賽隊的參賽場次、兩場間隔和總場次數

（一）編程思路

1.輸入參賽隊數目n和賽程安排表儲存矩陣A，輸出每個參賽隊的參賽場次矩陣P，間隔場次數矩陣J，其中從第一行到第n行分別為1號到n號參賽隊的參賽場次和間隔場次。輸出每個參賽隊的總間隔場次數向量D。

2.先按奇數列和偶數列分別計算每個參賽隊參加的場次數，儲存在矩陣T中。若T中有0，去除0后，儲存在P中。若T中沒有0,對于矩陣P的行，按從小到大的順序排列，即對應每個參賽隊參加的場次數從小到大的順序。對于矩陣P，按行計算間隔場次數后儲存在矩陣J中輸出，即為每個隊的間隔場次數。對于矩陣J按行求和后儲存在向量D中輸出，即為每個參賽隊的總場次數。

（二）MATLAB程序

（三）結果驗證

1.構造推理法

在命令窗口輸入〉〉n=21;A=gztlf(n);[P J D]=jg(n,A)，運行程序，根據運行結果得n=21時每個參賽隊參加的場次數、每兩場間隔場次數和總場次和如下：

表4 n=21時參賽隊參加的場次數

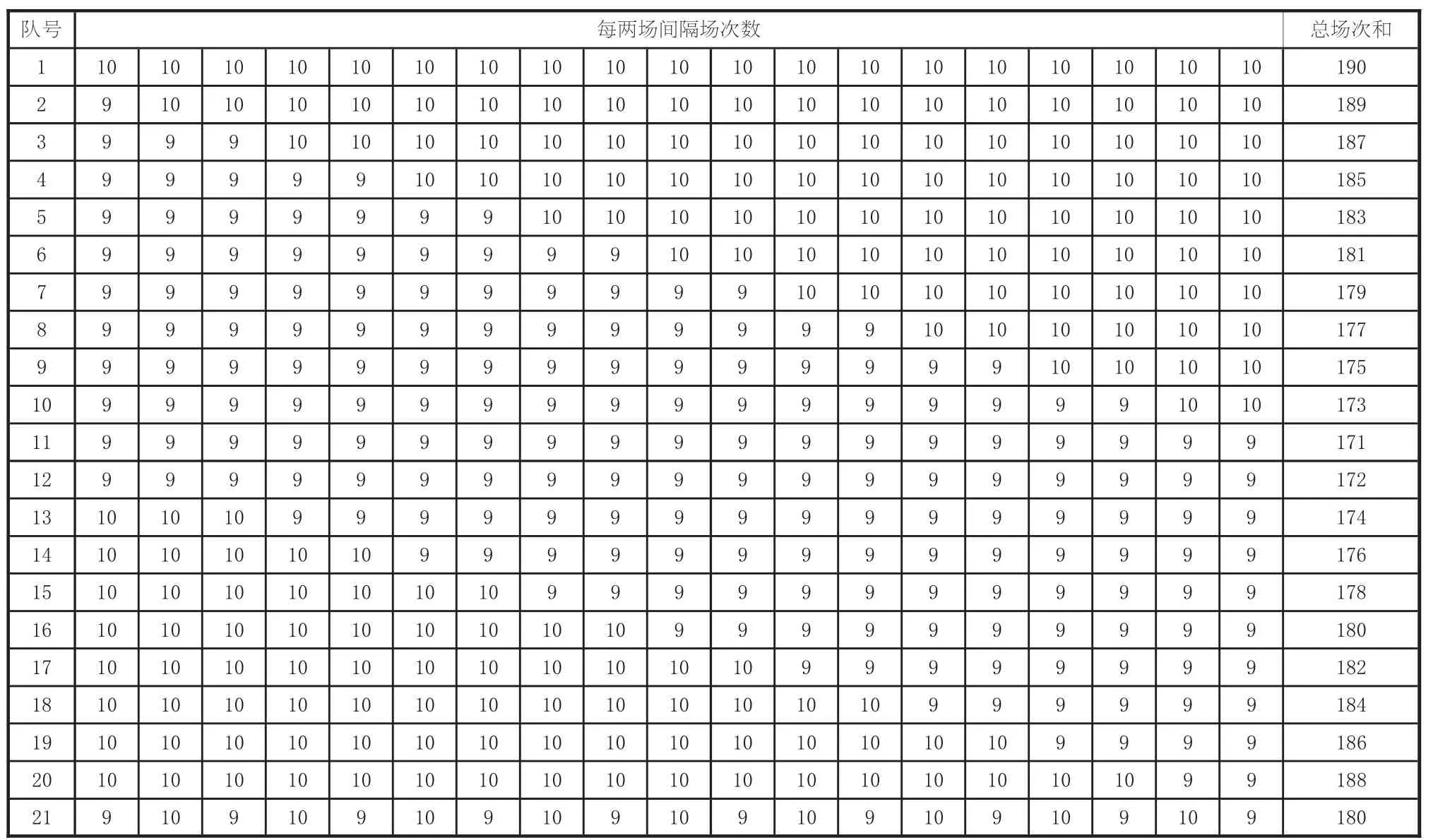
表5 n=21時每兩場間隔場次數和總場次和

2.圖論法

在命令窗口輸入〉〉n=21;A=tulun(n);[P J D]=jg(n,A)，運行程序，根據運行結果，筆者發現圖論法得到的每個參賽隊參加的場次數、每兩場間隔場次數和總場次與構造推理法的結論表4、表5行不同而已。

3.改進的貝格爾編排法

在命令窗口輸入〉〉n=20;A=gjb(n);[P J D]=jg(n,A)，運行程序，根據運行結果得n=20時每個參賽隊參加的場次數、每兩場間隔場次數和總場次和如下：

表6 n=20時參賽隊參加的場次數

表7 n=20時每兩場間隔場次數和總場次和

表7 n=20時每兩場間隔場次數和總場次和