一種針對非合作目標(biāo)的雙站固定兩坐標(biāo)雷達(dá)系統(tǒng)誤差修正方法
尚 娟,姚 遠(yuǎn)
(中國船舶重工集團(tuán)公司第七二四研究所,南京211153)
0 引 言
在多雷達(dá)目標(biāo)跟蹤系統(tǒng)中,利用多源數(shù)據(jù)融合技術(shù)處理來自各雷達(dá)的量測數(shù)據(jù),具有降低虛警率、增大數(shù)據(jù)覆蓋范圍,以及提高目標(biāo)探測與跟蹤能力等優(yōu)點(diǎn)[1]。在融合的過程中,由于存在雷達(dá)對目標(biāo)探測的異步性、雷達(dá)固有的系統(tǒng)誤差、雷達(dá)探測數(shù)據(jù)的隨機(jī)誤差導(dǎo)致多雷達(dá)探測數(shù)據(jù)直接融合出現(xiàn)精度下降等問題。為了改善直接數(shù)據(jù)融合帶來的精度下降問題,在多雷達(dá)目標(biāo)跟蹤系統(tǒng)中需要通過空間配準(zhǔn)的方法校準(zhǔn)雷達(dá)的系統(tǒng)誤差。
本文采用精確極大似然空間配準(zhǔn)算法[2](EML)來實(shí)現(xiàn)基于非合作目標(biāo)的雙站固定雷達(dá)的二維系統(tǒng)誤差修正。文中詳細(xì)描述了雙站固定雷達(dá)系統(tǒng)誤差修正算法在多雷達(dá)目標(biāo)跟蹤系統(tǒng)中的結(jié)構(gòu)設(shè)計(jì)、處理流程及實(shí)現(xiàn)方法,最后通過實(shí)驗(yàn)室仿真的數(shù)據(jù)和外場采集的實(shí)測數(shù)據(jù)對優(yōu)化后的EML算法性能進(jìn)行了測試。
1 EML算法結(jié)構(gòu)模型
文中所述的精確極大似然空間配準(zhǔn)(EML)算法被設(shè)計(jì)成相對獨(dú)立的算法處理單元,通過接收多雷達(dá)目標(biāo)跟蹤系統(tǒng)發(fā)送的估算系統(tǒng)誤差命令來觸發(fā)估算處理。算法處理結(jié)構(gòu)如圖1所示。
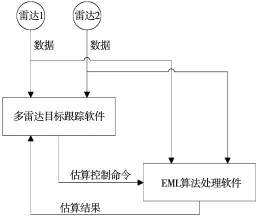
圖1 系統(tǒng)誤差配準(zhǔn)技術(shù)實(shí)現(xiàn)的軟件架構(gòu)
算法處理單元主要完成兩部雷達(dá)點(diǎn)跡數(shù)據(jù)預(yù)處理、點(diǎn)跡數(shù)據(jù)的編排、點(diǎn)航關(guān)聯(lián)和航跡濾波的功能。在點(diǎn)跡數(shù)據(jù)預(yù)處理中包括兩部雷達(dá)點(diǎn)跡數(shù)據(jù)的系統(tǒng)誤差修正。由于系統(tǒng)誤差在一段時(shí)間內(nèi)具有時(shí)不變的特性,不需要實(shí)時(shí)更新估算結(jié)果,所以在設(shè)計(jì)算法結(jié)構(gòu)時(shí)通過發(fā)送命令的方式來控制EML算法處理的時(shí)機(jī)。
多雷達(dá)EML算法處理在兩部雷達(dá)的共視區(qū)域內(nèi)挑選穩(wěn)定跟蹤的目標(biāo),將目標(biāo)的航跡信息作為估算控制命令發(fā)送至EML算法處理軟件。EML算法處理軟件中存在兩個(gè)跟蹤器與兩部雷達(dá)一一對應(yīng),在接收到估算控制命令后兩個(gè)跟蹤器分別完成各自航跡的建立并維持跟蹤。跟蹤器內(nèi)維持的航跡數(shù)據(jù)作為EML算法的估算數(shù)據(jù)來源,當(dāng)數(shù)據(jù)積累個(gè)數(shù)滿足EML算法要求后啟動(dòng)算法迭代計(jì)算,得到估算結(jié)果。EML算法處理單元組成如圖2所示。
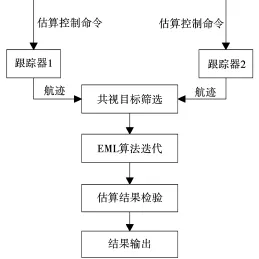
圖2 EML算法處理軟件組成
2 算法實(shí)現(xiàn)方法
2.1 共視目標(biāo)匹配技術(shù)
在本文針對的系統(tǒng)誤差修正的場景中是不存在合作目標(biāo)的,所以需要挑選兩部雷達(dá)的共視目標(biāo)作為EML算法的作用對象。共視目標(biāo)在本文內(nèi)被定義為位于兩部雷達(dá)的共同探測區(qū)域內(nèi)并能夠被各雷達(dá)有效探測并穩(wěn)定跟蹤的目標(biāo)。共視目標(biāo)的航跡數(shù)據(jù)作為EML算法的輸入被當(dāng)作用EML算法修正兩部雷達(dá)系統(tǒng)誤差的依據(jù)。
EML算法處理單元中的兩個(gè)跟蹤器將目標(biāo)航跡數(shù)據(jù)存入共視目標(biāo)篩選模塊中的數(shù)據(jù)緩存內(nèi)。共視目標(biāo)篩選模塊按照以下的步驟實(shí)現(xiàn)共視目標(biāo)的篩選:
(1)截取公共時(shí)間段
兩個(gè)跟蹤器中的目標(biāo)在建航時(shí)存在時(shí)間上差異,在跟蹤過程中由于不同目標(biāo)的狀態(tài)不一致,故每一個(gè)目標(biāo)的生存周期也是不一樣,所以需要對緩存中記錄的目標(biāo)航跡數(shù)據(jù)進(jìn)行“裁剪”。“裁剪”的原則以被記錄目標(biāo)的第1個(gè)航跡數(shù)據(jù)時(shí)間中最遲的那一個(gè)時(shí)刻作為公共時(shí)間段的起點(diǎn),以被記錄目標(biāo)的最后一個(gè)航跡數(shù)據(jù)時(shí)間中最早的那一個(gè)時(shí)刻作為公共時(shí)間段的終點(diǎn)。
(2) 內(nèi)插外推時(shí)間對齊[3]
共視目標(biāo)在兩部雷達(dá)的共同探測區(qū)域內(nèi)產(chǎn)生航跡數(shù)據(jù),而通常情況下兩部雷達(dá)對目標(biāo)的探測是不同步的。為了滿足假設(shè)檢驗(yàn)對輸入數(shù)據(jù)的要求,需要對經(jīng)過“裁剪”具有公共時(shí)間段的航跡數(shù)據(jù)進(jìn)行時(shí)間上的對齊,本文采用的方式是“內(nèi)插外推”。
(3)建立假設(shè)統(tǒng)計(jì)量進(jìn)行航跡互聯(lián)[4]
假設(shè)兩部雷達(dá)對目標(biāo)濾波后的估計(jì)誤差獨(dú)立,構(gòu)造統(tǒng)計(jì)量如下:
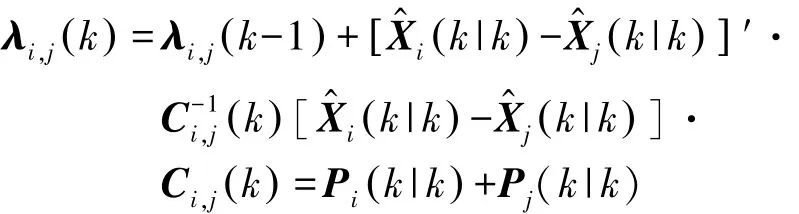
式中,(k|k)表示雷達(dá) a 中對目標(biāo) i的狀態(tài)估計(jì),(k|k)表示雷達(dá) b中對目標(biāo) j的狀態(tài)估計(jì),Pi(k|k)表示雷達(dá)a中對目標(biāo)i的狀態(tài)協(xié)方差估計(jì),Pj(k|k)表示雷達(dá)b中對目標(biāo)j的狀態(tài)協(xié)方差估計(jì)。
根據(jù)雷達(dá)a中的N個(gè)目標(biāo)航跡、雷達(dá)b中的M個(gè)目標(biāo),得到λ的一個(gè)N×M的矩陣。遍歷該矩陣,當(dāng)矩陣中λ(i,j)的值小于ε的時(shí)候,認(rèn)為雷達(dá)a中的第i個(gè)目標(biāo)和雷達(dá)b中的第j個(gè)目標(biāo)為共視目標(biāo),ε的取值和系統(tǒng)誤差及測量的隨機(jī)誤差有關(guān)。ε在本文描述的情況下取值為1e-5。
2.2 基于量測噪聲的極大似然法修正技術(shù)
考慮兩個(gè)雷達(dá)a和b對同一目標(biāo)的斜距和方位進(jìn)行量測,配準(zhǔn)誤差的幾何關(guān)系如圖3所示。
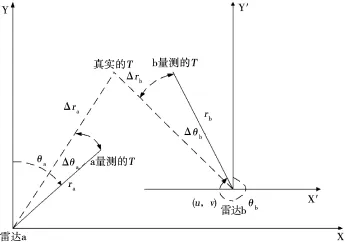
圖3 EML空間誤差配準(zhǔn)的幾何關(guān)系圖
假定雷達(dá)a位于坐標(biāo)原點(diǎn),雷達(dá)b在公共坐標(biāo)系中的位置為(u,v)。 用 T 表示目標(biāo),(ra,k,θa,k)和(rb,k,θb,k)分別表示雷達(dá)a和雷達(dá)b對目標(biāo)的斜距和方位角量測,(Δra,Δ θa)和(Δrb,Δ θb)分別表示雷達(dá) a 和 b的斜距和方位角偏差。
由圖3所示的配準(zhǔn)誤差幾何關(guān)系可得:
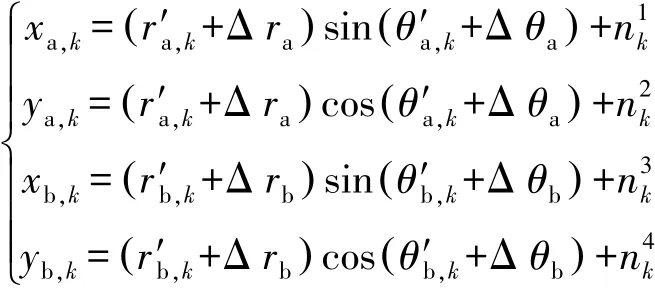
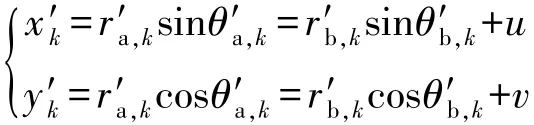
將上式代入一階線性展開的公式中可得
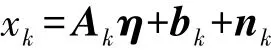
極大似然方法是基于雷達(dá)量測的似然函數(shù)工作的。假定量測噪聲服從正態(tài)分布,根據(jù)該噪聲分布的條件密度函數(shù)建立相應(yīng)的負(fù)對數(shù)似然函數(shù),然后建立約束條件為雷達(dá)量測誤差η= (Δra,Δ θa,Δrb,Δθb) 和目標(biāo)真實(shí)位置ξ= (x′k,y′k) 的似然函數(shù)優(yōu)化問題。
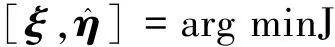
其中

采用交替優(yōu)化的技術(shù)對,進(jìn)行序貫優(yōu)化,直到收斂。因?yàn)镴是的非線性函數(shù),通常得不到解析解。但是,由于與η是分離的,所以可以利用交替優(yōu)化的方法對,進(jìn)行序貫優(yōu)化。
2.3 最小二乘檢驗(yàn)技術(shù)
為了防止EML算法在迭代的過程中收斂到局部最小值,需要對EML算法收斂后的結(jié)果進(jìn)行驗(yàn)證。由于沒有合作目標(biāo)的存在,無法得到真值信息,因此在篩選共視目標(biāo)時(shí)需要挑選出3組目標(biāo)。以3點(diǎn)定面的原理,將一組目標(biāo)用于EML算法迭代,另外兩組利用迭代的結(jié)果進(jìn)行航跡數(shù)據(jù)的修正,對修正之后的航跡數(shù)據(jù)進(jìn)行最小二乘檢驗(yàn)。如果通過檢驗(yàn)則EML算法的迭代結(jié)果有效,沒有通過檢驗(yàn)則需要修改EML算法中的迭代步長,重新迭代。
最小二乘檢驗(yàn)過程[5]描述如下:
假設(shè)通過共視目標(biāo)篩選獲取到3個(gè)共視目標(biāo)A、B、C。雷達(dá)a在公共時(shí)間段內(nèi)得到的目標(biāo)A的航跡數(shù)據(jù)為 [X1Aa,X2Aa,…,XkAa],雷達(dá)b在公共時(shí)間段內(nèi)得到的目標(biāo)A的航跡數(shù)據(jù)為 [X1Ab,X2Ab,…,XkAb]。
雷達(dá)a在公共時(shí)間段內(nèi)得到的目標(biāo)B的航跡數(shù)據(jù)為 [X1Ba,X2Ba,…,XkBa],雷達(dá)b在公共時(shí)間段內(nèi)得到的目標(biāo)B的航跡數(shù)據(jù)為 [X1Bb,X2Bb,…,XkBb]。
雷達(dá)a在公共時(shí)間段內(nèi)得到的目標(biāo)C的航跡數(shù)據(jù)為 [X1Ca,X2Ca,…,XkCa],雷達(dá)b在公共時(shí)間段內(nèi)得到的目標(biāo)C的航跡數(shù)據(jù)為 [X1Cb,X2Cb,…,XkCb]。
建立最小均方根計(jì)算公式:
利用EML算法迭代后得到的結(jié)果完成共視目標(biāo)A、B、C航跡數(shù)據(jù)的修正,然后計(jì)算Q值,之后在EML算法中調(diào)整步長值繼續(xù)迭代。步長值取值范圍:0.1∶0.1∶0.8。取Q最小時(shí)對應(yīng)EML算法結(jié)果為估算的系統(tǒng)誤差值。
3 仿真實(shí)驗(yàn)與分析
3.1 仿真結(jié)果
仿真場景:依據(jù)VTS導(dǎo)航雷達(dá)的外場數(shù)據(jù),通過人為添加系統(tǒng)誤差的方式制造出兩部雷達(dá)存在系統(tǒng)誤差和共視目標(biāo)的仿真場景。在該場景中,雷達(dá)a添加的系統(tǒng)誤差為-4.5°,800 m,雷達(dá)b添加的系統(tǒng)誤差為5.5°,-500 m。 兩部 VTS導(dǎo)航雷達(dá)沿長江布站,相距約12 km。VTS系統(tǒng)導(dǎo)航雷達(dá)的測量精度為距離20 m,方位 0.2°。
共視目標(biāo):選擇長江航道中的浮標(biāo)作為兩部雷達(dá)的校準(zhǔn)系統(tǒng)誤差的共視目標(biāo)。
在文中的仿真處理中,對于共視目標(biāo)積累的數(shù)據(jù)樣本數(shù)>30。

圖4 EML算法處理之前的點(diǎn)跡效果圖

圖5 EML算法處理之后的點(diǎn)跡效果圖

表1 仿真條件下系統(tǒng)誤差估算結(jié)果
通過仿真結(jié)果可以看出,文中的方法可以較好地實(shí)現(xiàn)系統(tǒng)誤差修正,其修正率能達(dá)到80%以上。但是,通常情況下系統(tǒng)誤差的修正率會(huì)受到雷達(dá)測量誤差、共視目標(biāo)積累數(shù)據(jù)長度、共視目標(biāo)運(yùn)動(dòng)狀態(tài)等因素的影響,其定量的分析有待深入研究。文中提及的方法在系統(tǒng)誤差相比雷達(dá)測量誤差較顯著、共視目標(biāo)積累數(shù)據(jù)較多且共視目標(biāo)運(yùn)動(dòng)狀態(tài)較穩(wěn)定的條件下具有較好的空間配準(zhǔn)性能。
3.2 實(shí)測跑船結(jié)果
結(jié)合外場實(shí)驗(yàn),測試經(jīng)EML算法估算系統(tǒng)誤差之后目標(biāo)跟蹤的穩(wěn)定性和跟蹤精度的效果。
測試場景:A、B站兩部雷達(dá)工作主動(dòng)工作方式下,將兩臺(tái)雷達(dá)的天線掃描范圍調(diào)至具有共視區(qū)域的位置,開啟雷達(dá)發(fā)射功能,要求單雷達(dá)對目標(biāo)的檢測概率達(dá)到50%以上,并且要求兩部雷達(dá)具有相同或者近似的數(shù)據(jù)更新率。在兩部雷達(dá)點(diǎn)跡融合跟蹤的顯控界面上進(jìn)行多批目標(biāo)人工錄取,待目標(biāo)跟蹤穩(wěn)定后進(jìn)行航跡數(shù)據(jù)的采集。在試驗(yàn)中以1 h為時(shí)間間隔,將兩部雷達(dá)的航跡數(shù)據(jù)和點(diǎn)跡融合軟件的航跡數(shù)據(jù)導(dǎo)出。根據(jù)導(dǎo)出的航跡數(shù)據(jù)計(jì)算跟蹤精度。
測試結(jié)果:圖6所示為點(diǎn)跡融合對海配合目標(biāo)的跟蹤結(jié)果,◇為點(diǎn)跡融合跟蹤結(jié)果,○為對應(yīng)時(shí)刻的GPS真值。
圖7所示為雷達(dá)a對海配合目標(biāo)的跟蹤結(jié)果,圖中?為雷達(dá)a對海配合目標(biāo)的跟蹤結(jié)果,○為對應(yīng)時(shí)刻的GPS真值。雷達(dá)a并沒有能夠?qū)υ撃繕?biāo)進(jìn)行全程的跟蹤。

圖6 點(diǎn)跡融合跟蹤的航跡和真值
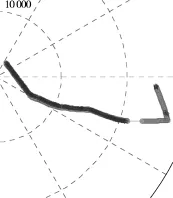
圖7 雷達(dá)a跟蹤的航跡和真值
圖8所示為雷達(dá)b對海配合目標(biāo)的跟蹤結(jié)果,圖中☆為雷達(dá)b對海配合目標(biāo)的跟蹤結(jié)果,○為對應(yīng)時(shí)刻的GPS真值。雷達(dá)b收到其他目標(biāo)的干擾在跟蹤過程中3次跟丟目標(biāo),在數(shù)據(jù)中有4個(gè)批號(hào)的航跡數(shù)據(jù)與之對應(yīng)。
以雷達(dá)b對應(yīng)目標(biāo)位置的4批航跡為測試間隔,計(jì)算點(diǎn)跡融合軟件對目標(biāo)的跟蹤精度。4段的時(shí)間間隔為:第1段為54 121~59 015 s,第2段為59 168~59 714 s,第3段為 59 935~61 066 s,第 4段為 61 332~62 663 s。
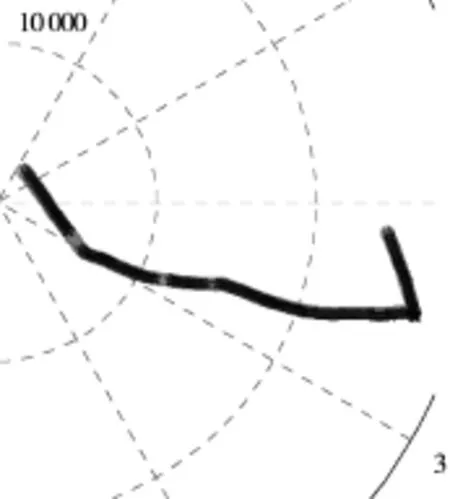
圖8 雷達(dá)b跟蹤的航跡和真值
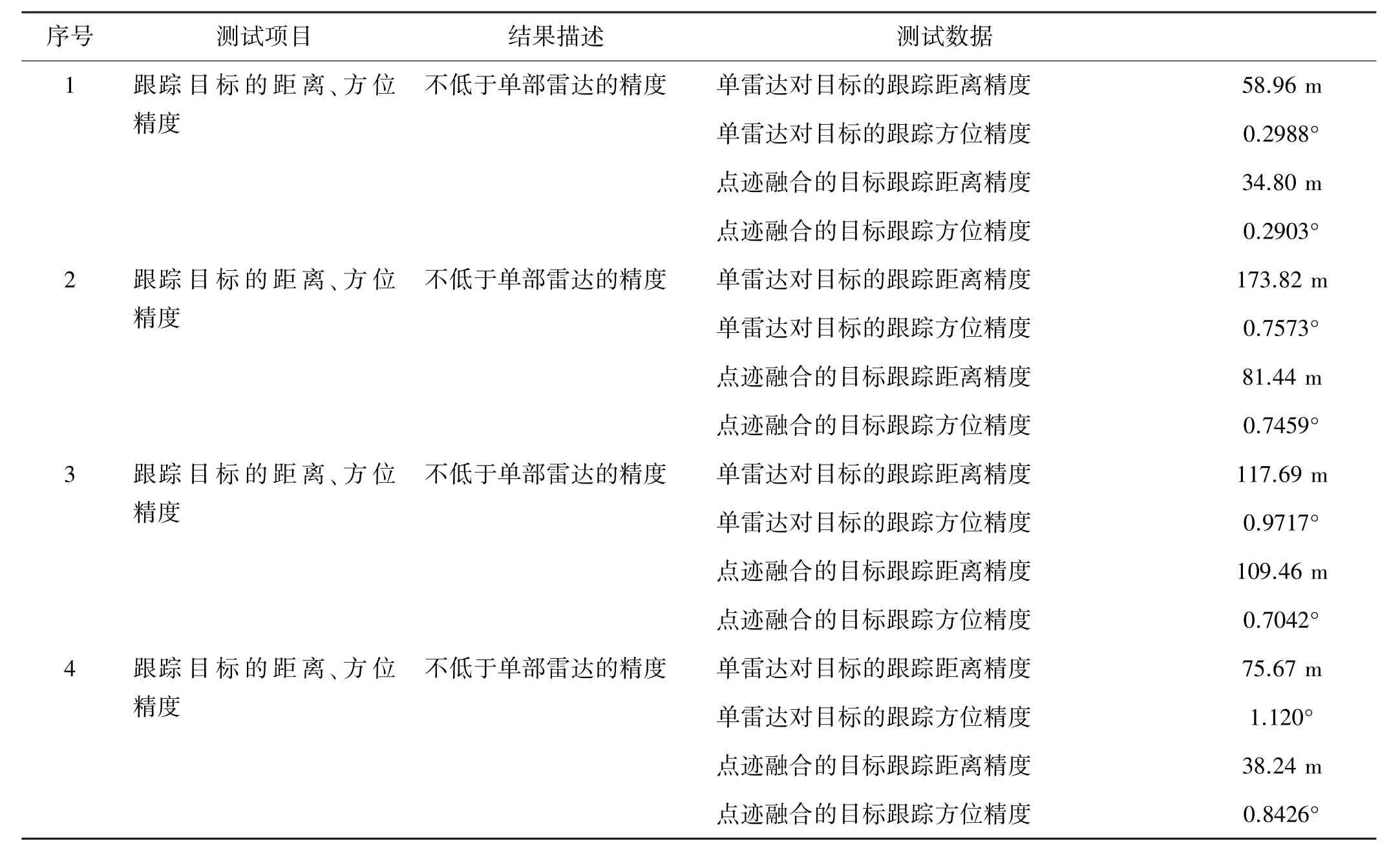
表2 跟蹤目標(biāo)的距離、方位精度計(jì)算結(jié)果
4 結(jié)束語
本文基于非合作目標(biāo)場景提出了雙站固定雷達(dá)二維系統(tǒng)誤差估計(jì)的工程實(shí)現(xiàn)方法。文中在EML算法估算系統(tǒng)誤差的基礎(chǔ)上提出了一種EML算法輸入數(shù)據(jù)的預(yù)處理方法。該方法可以實(shí)現(xiàn)雙站雷達(dá)共視目標(biāo)的自動(dòng)匹配,完成共視目標(biāo)航跡數(shù)據(jù)的時(shí)間配準(zhǔn)。考慮EML算法在目標(biāo)位置真值和雷達(dá)系統(tǒng)誤差迭代求解中容易陷入局部最小值的缺陷,文中又提出了基于最小二乘理論的數(shù)據(jù)檢查方法,進(jìn)一步提高了估計(jì)結(jié)果的準(zhǔn)確性。最后通過實(shí)驗(yàn)室仿真的數(shù)據(jù)和外場采集的實(shí)測數(shù)據(jù)對文中提出的雙站固定雷達(dá)二維系統(tǒng)誤差修正技術(shù)進(jìn)行了測試。結(jié)果表明,空間配準(zhǔn)處理后可以有效提高融合航跡的位置精度。在文中所述的兩部同型雷達(dá)以相同的掃描策略對共視區(qū)內(nèi)目標(biāo)進(jìn)行探測的條件下,通過試驗(yàn)數(shù)據(jù)的分析,雙站雷達(dá)的點(diǎn)跡融合航跡,其位置精度不低于單部雷達(dá)航跡的位置精度[6]。
文中提出的方法,雖然不要求目標(biāo)具有真值,但是對共視目標(biāo)的個(gè)數(shù)、積累數(shù)據(jù)的長度、共視目標(biāo)的運(yùn)動(dòng)狀態(tài)以及系統(tǒng)誤差相比隨機(jī)誤差的顯著程度提出了要求,不具備普遍適用性。該方法適用于無法利用合作目標(biāo)進(jìn)行雷達(dá)標(biāo)定的場合。

