彈道導彈群目標多普勒速度估計算法

靳俊峰，曾 怡，廖圣龍

（中國電子科技集團公司第三十八研究所孔徑陣列與空間探測安徽省重點實驗室，合肥230088）

0 引 言

為了提高突防能力，彈道導彈在飛行中段經常會采用投放干擾箔條和模擬彈頭的假目標，或將末級火箭炸成碎片形成干擾碎片云等突防措施。由于在飛行中段沒有大氣阻力，彈頭、誘餌、整流罩、母艙、碎片殘骸等均在彈道附近伴隨著彈頭高速運動，在空間形成擴散范圍達幾千米、相互靠近的群目標［1］。

雷達在對導彈群目標進行多普勒測速時，由于群內目標密集度高、位置變化隨機性強、相互遮擋嚴重，無法對群內目標單獨進行測速，會發生多普勒速度大幅跳動情況，嚴重影響目標測距精度，導致在目標關聯過程中經常出現混批、錯批，給后續的目標識別、軌道外推等帶來很大難度，嚴重時甚至會丟失目標。如何解決群目標多普勒速度估計是實現群內目標正確關聯的核心問題［2］。

在航天測控領域中，一般采用多測速系統實現外空間飛行器的高精度測速，且僅限于合作的單目標。但是，在彈道導彈預警系統中，雷達面對的是飽和攻擊，彈頭、誘餌、干擾、配重等會形成群目標，直接進行多普勒測速會由于密集目標遮擋等原因測速不準，此外測量的速度也無法與群目標進行一一對應，增大了航跡跟蹤難度。

本文提出了一種新的彈道導彈群目標多普勒速度估計算法。首先將量測多普勒距離補償去掉，這樣群目標在多幀之間可保持距離量測的一致性，不會由于多普勒速度測量的跳動導致群目標多幀之間相關錯誤，然后采用最優分配策略進行群目標關聯［3］，并采用基于彈道導彈動力學的UKF濾波算法進行目標位置、速度估計，最后根據濾波結果進行多普勒速度重新估計，目標距離經多普勒重新補償后進行上報。

1 多普勒補償

彈道導彈相對雷達高速運動時，由于傳播路程差的原因，跟蹤過程中會出現跨距離單元、跨多普勒單元現象，使雷達系統常用的相參積累處理失效。必須通過對目標回波信號進行速度、加速度補償才能實現有效的積累［4］。

假設目標相對雷達多普勒速度為Vr，向站運動時多普勒速度為正，背向雷達運動時多普勒速度為負，雷達帶寬為Bw，發射脈沖寬度為Pw，工作頻點為Fr，則目標多普勒補償距離為

在群目標跟蹤過程中，由于群內目標互相遮擋，雷達無法直接測量群中每批目標的多普勒速度，而只能通過測量群目標回波中的峰值作為群目標多普勒速度。事實上群內目標速度是有差別的。顯然，通過直接測量群目標多普勒速度進行距離補償引入了人為誤差，會導致后續相關、濾波出現錯誤。因此，需要對群目標量測距離進行去多普勒補償。假設時刻t某量測距離為R（t），則去多普勒補償距離為

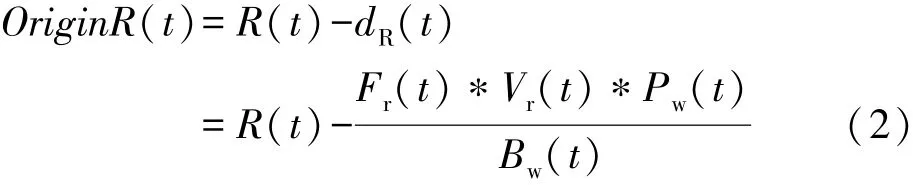
雷達處理多普勒補償時可以取脈沖前沿或后沿，此時多普勒補償正負方向會相反，只需要在上面公式中改變正負號即可。后續的相關、濾波處理均使用去多普勒補償距離。

2 基于綜合多因子關聯矩陣的最優分配算法

2.1 關聯矩陣

關聯矩陣是表示兩個實體之間相似性程度的度量，對每一個“量測?航跡”對都必須計算其關聯矩陣。關聯概率大小取決于特征向量的隸屬度和權向量，通過歸一化模糊評判向量和權向量構成綜合隸屬度評判函數［5］，航跡i與量測j的目標關聯概率為

關聯概率dij若小于閾值Pth，則認為航跡i與量測j無法關聯，在關聯矩陣中取值為0；若大于Pth，則可用于構建基于綜合隸屬度函數的關聯矩陣IM：

其中，n表示航跡數，m表示量測數。

2.2 最優分配

彈道目標關聯問題采用綜合隸屬度函數表示為關聯矩陣后，對時刻k所有的量測與航跡關聯的核心就是如何對關聯矩陣進行分配。該分配問題可描述如下：

給定關聯矩陣IM，對矩陣中的每個元素aij，找到一個分配X＝｛xij｝，使得總的隸屬度Subjection＝最小化，同時滿足以下限制：（1）任一量測j最多僅與一個航跡i關聯，即＝1?i；

（2）一個航跡i最多僅與一個量測j關聯，即＝1?j。

在分配算法中，允許xij為0或者1。如果量測數少于航跡數，則會出現有些航跡無法分配到量測，會出現量測無法關聯到航跡。

對分配問題采用一種最優分配算法解決，步驟如下：

（1）首先對關聯矩陣IM采用聚類算法進行分簇，滿足簇內的量測與航跡綜合隸屬度大于0，而簇間的量測與航跡綜合隸屬度為0。通過分簇可將規模較大的分配問題轉換為規模較小的分配問題，減少計算量；

（2）對關聯矩陣IM每一行，找出最小的元素rowmin，并將該行中的所有元素減去該值；

（3）對關聯矩陣IM每一列，找出最小的元素colmin，并將該列中的所有元素減去該值；

（4）比較矩陣行數n和列數m，不妨假設行數n小于列數m，統計最少需要多少直線來覆蓋結果矩陣中出現的所有零值，如果此時的零值個數與n相同，找到最優分配，矩陣計算結束，否則轉第5步；

（5）找出第4步中未被直線覆蓋的最小非零值a，所有未被覆蓋的元素減去a，對于被兩條直線交叉覆蓋的非零元素加a，重復第4步。

采用最優分配算法可以完成群內密集目標量測與航跡的準確配對。這是后續濾波、多普勒速度估計的基礎。

3 彈道導彈動力學模型

根據彈道導彈從發射點到目標點的運動過程中的受力情況，可將其彈道分為3段。首先，根據導彈在飛行中發動機和控制系統工作與否，可將其彈道分為動力飛行段（簡稱主動段）和無動力飛行段（簡稱被動段）兩部分。其次，在被動段則又根據彈頭所受空氣動力的大小分為自由飛行段（簡稱自由段）和再入大氣層飛行段（簡稱再入段）兩部分［6?7］。 表1給出了彈道飛行模型各段的飛行階段及其受力情況。

表1 彈道導彈飛行階段及其受力情況

3.1 主動段彈道目標運動模型

在地心地固坐標系ECEF下，設目標位置向量為p＝［px，py，pz］′，速度向量v＝［vx，vy，vz］′。 通過上述分析，可以建立彈道目標主動段的方程。

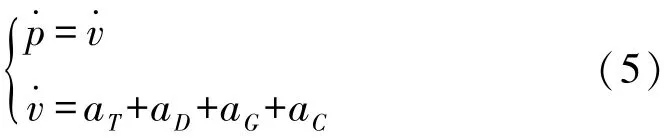
彈道目標主動段上的加速度主要分為4項：aT推進力產生的加速度，aD空氣阻力產生的加速度，aG地心引力產生的加速度，aC外在力（科氏力和離心力）產生的加速度。

3.2 自由段彈道目標運動模型

自由段上的加速度的包括aG地心引力產生的加速度、aC外在力（科氏力和離心力）產生的加速度，可以得到自由段的運動方程：

3.3 再入段彈道目標運動模型

再入段上的加速度包括aD空氣阻力產生的加速度、aG地心引力產生的加速度、aC外在力（科氏力和離心力）產生的加速度，可以得到再入段的運動方程：

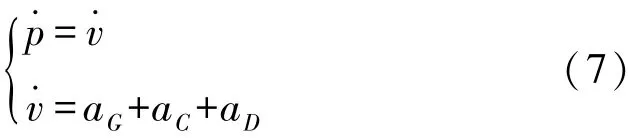
4 群目標多普勒速度估計

根據彈道導彈動力學模型，采用UKF濾波算法可以得到目標精確的速度、加速度估計。假設某批目標站心坐標系下的時刻t濾波結果為X（t）、Y（t）、Z（t）、Vx（t）、Vy（t）、Vz（t），則可以得到該時刻的濾波多普勒速度為

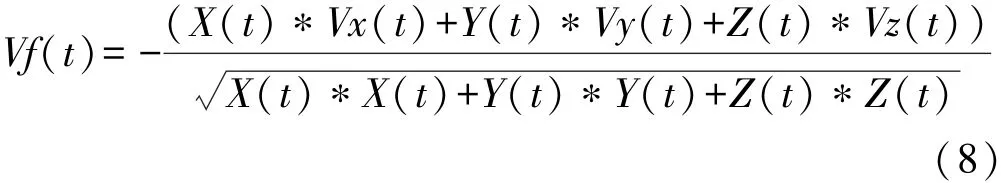
目標上報時可根據重新估計的多普勒速度進行距離補償。該結果對群目標來講明顯好于脈沖多普勒測速直接補償結果。

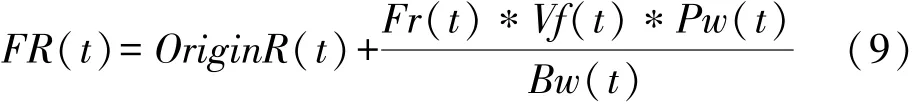
主要處理步驟：

（1）判斷彈道導彈量測是否為群目標，如果是則對群目標量測距離進行去多普勒補償，否則采用PD測速方式對單目標進行測速；

（2）對群目標建立量測?航跡關聯矩陣，關聯矩陣通過綜合隸屬度方法進行計算，并采用最優分配算法進行配對分配；

（3）對配對好的量測?航跡采用基于彈道導彈動力學的UKF濾波方法進行濾波，估計目標在站心系中的位置和速度；

（4）根據目標位置和速度計算多普勒速度，并在目標上報時根據該速度進行重新多普勒補償。

彈道導彈群目標多普勒速度估計處理流程如圖1所示。

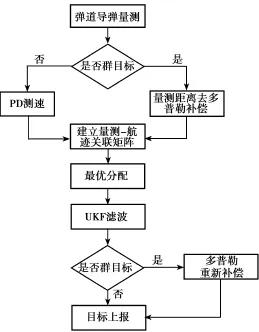
圖1 彈道導彈群目標多普勒速度估計流程

5 算法分析

為了更真實仿真群目標過程，本文假設有7發導彈集火射擊，仿真產生的飛行軌跡數據加入量測噪聲。假設雷達工作頻段為P波段，工作頻點575 MHz，信號帶寬2 MHz，對RCS為1 m2目標作用距離1 000 km，距離測量精度為50 m，方位角量測精度為0.2°，仰角量測精度為 0.2°，跟蹤數據率為2 Hz。

彈道導彈飛行射程為600 km，飛行時間為520 s，飛行最大高度為215 km，雷達站位置距發射點距離為353.84 km。在彈道導彈飛行過程中生成了彈頭群和彈體群目標，其中彈頭群中包含7個目標，彈體群包含7個目標。

圖2表示直接采用脈沖多普勒速度補償距離進行目標跟蹤結果。跟蹤過程中發生了多次混批，且跟蹤質量較差，起伏較大，不能夠滿足后續目標識別、彈道計算要求。

圖3為采用本文算法跟蹤結果。可見，去掉多普勒補償后，由于目標在幀間能夠保持一致性，有助于量測和航跡間的最優分配，經濾波后重新估計多普勒速度輸出，可看出目標跟蹤連續，相關正確率也大幅提高。

圖2基于量測多普勒的群目標跟蹤

圖3 基于估計多普勒的群目標跟蹤

6 結束語

彈道導彈群目標跟蹤是構建防空反導體系的重要組成部分，也是完善戰略預警體系的一個重要環節。針對彈道導彈群目標多普勒速度量測精度差、前后幀不一致問題，本文通過對大量實測數據事后分析及實測驗證，提出了4步法彈道導彈群目標多普勒估計算法，即去多普勒補償、最優分配、濾波估計、重新多普勒補償。算法分析中設計了7發彈道導彈的復雜場景。結果表明，本文算法能夠對彈道導彈群目標多普勒速度進行準確估計，相比直接測量多普勒速度有極大提高，特別在集火攻擊等極端復雜情況下仍然能夠給出準確速度估計。