基于部隊移動模式三方作戰Lanchester模型研究
田寶國,盧 翰,叢 凱
(海軍航空大學, 山東 煙臺 264001)
1914年,英國工程師F.W.Lanchester提出Lanchester方程[1],首次使用數學方法定量分析戰爭結果與作戰雙方兵力規模和火力強弱的關系。現在有許多學者針對該類方程的線性率和平方率進行研究[2-4],并針對不同情況對方程進行補充與拓展[5-11]。但是,隨著武器裝備和戰術戰法的更新,戰場的環境也更加復雜,傳統的Lanchester作戰模型已經不適用于現代戰爭。于是人們在之前研究的基礎上提出空間Lanchetser作戰模型。考慮到在實際作戰中部隊在空間中的移動和部隊間的相互作用,Protopoprecu等[12-13]提出空間Lanchester偏微分方程模型,同時Cosner等[14]采用具有非線性相互作用的拋物線微分方程對該模型進行理論分析。考慮到具體的空間情況,Spradlin等[15]將Lanchester方程的直接瞄準和間接瞄準進行拓展研究,并提出三維時空Lanchetser作戰模型。對于三方作戰的研究目前處于起步階段[16],只是根據傳統Lanchester作戰模型拓展到三方作戰階段,并沒有考慮到空間因素對三方作戰結果的影響。同時,在當今世界出現三方作戰的情況比如波斯尼亞內戰、伊拉克內戰和敘利亞動亂[17],基本上都是在比較復雜的山地與城市中,此時部隊移動模式將對作戰結果造成影響。本文對三方作戰中部隊移動模式進行分類分析并對其時空動力學進行研究。
1 短距移動模式
1.1 短距移動模式三方Lanchester作戰模型
建立一個規模為M×N的平面二維網格,采取周期邊界條件,在網格中存在A,B,C三方兵力,分別用紅,黃,藍三種顏色表示,在每一個網格中只能存在一種兵力,空格φ表示此處沒有任何一方的兵力,用灰色表示。A,B,C三方和空格φ之間的關系如下所示:
(1)
(2)
其中,式(1)中μ為交戰率,表示兩個存在不同方兵力的網格間的發生交戰并且一方占領另一方的網格的概率,體現了交戰方的作戰與支援能力。在實際作戰中指不同部隊間發現并交火的可能性。式(2)中σ為轉移率,表示存在兵力的網格向空網格的轉移概率,體現了交戰方的個體流動性。在實際作戰中指部隊在區域中移動的概率。
采用蒙特卡洛隨機模擬方法,具體步驟如下:
步驟1:在整個網格中隨機選擇一個存在兵力的網格;
步驟2:判別已經選擇的網格的上下左右四個方向的網格狀態;
步驟3:隨機選擇一個方向的網格,按照式(1)或者式(2)的反應方程進行反應;
步驟4:重復步驟1直至仿真結束。
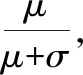
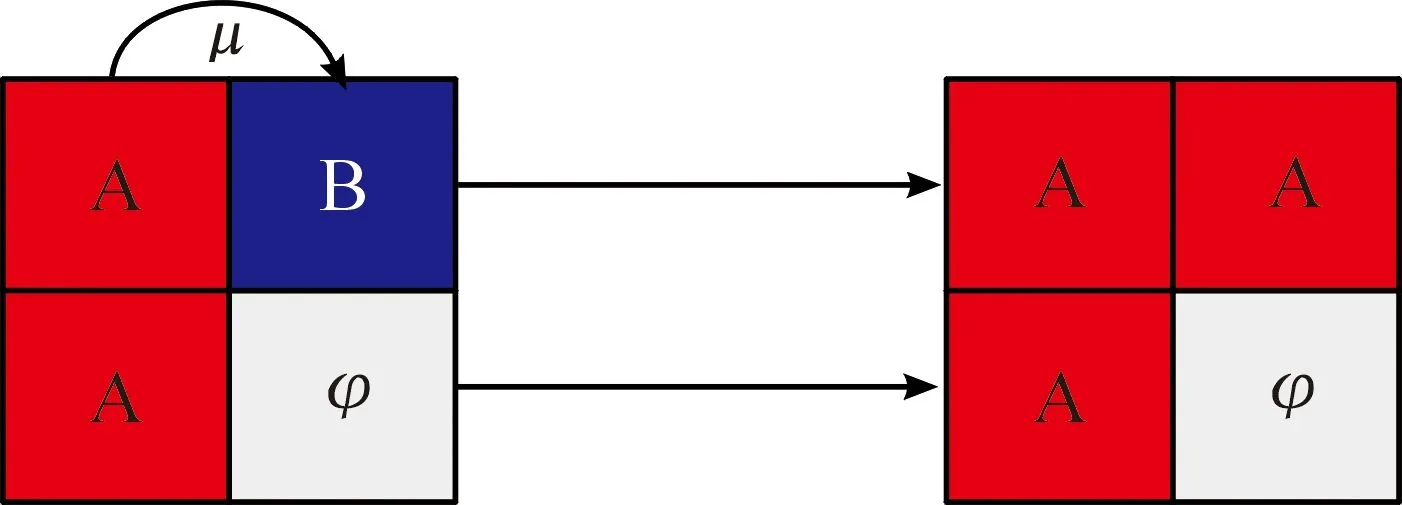
圖1 在交戰率為μ時A與B的交戰反應
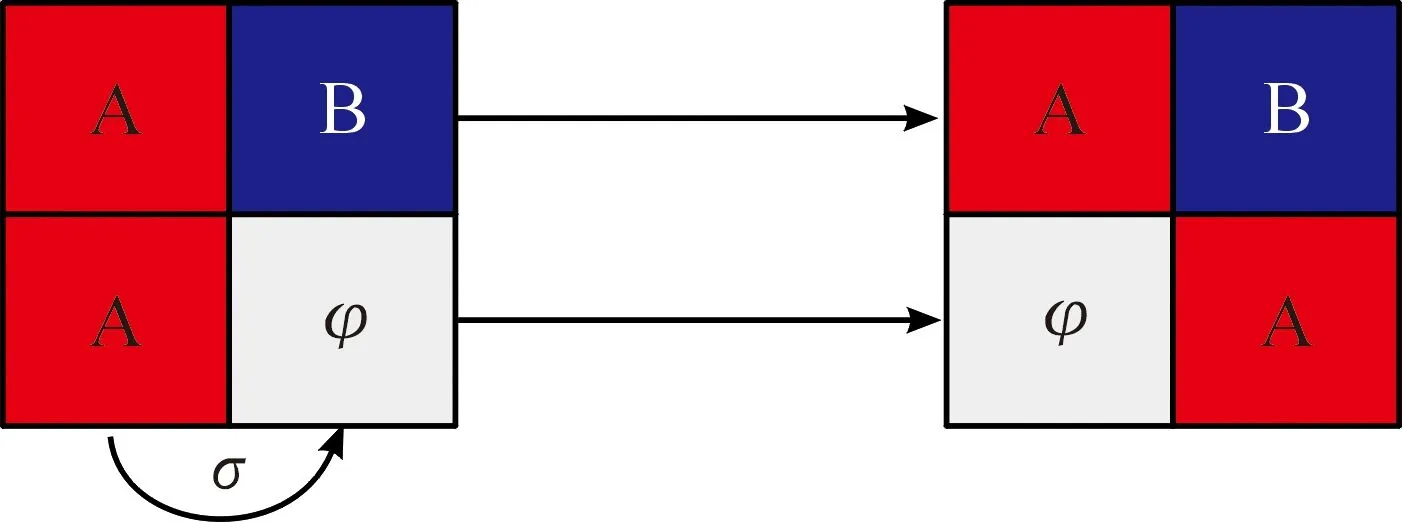
圖2 在轉移率為σ時A與φ的交換反應
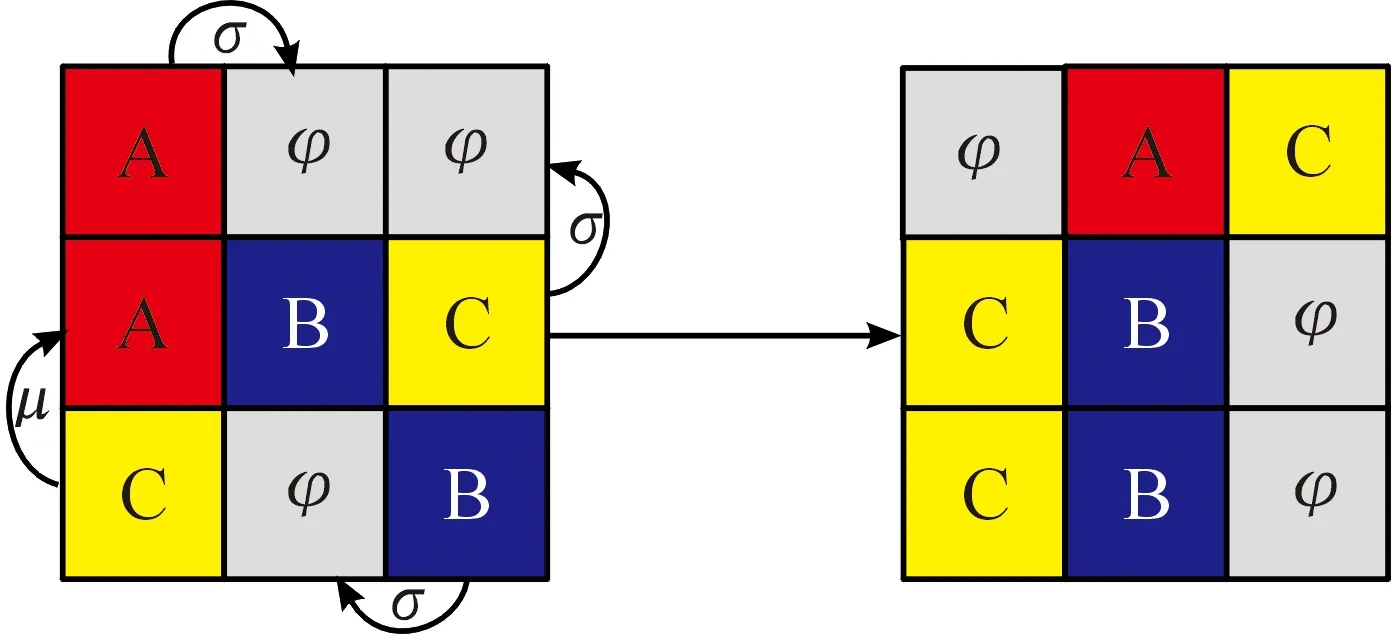
圖3 交戰反應與交換反應
1.2 交戰率—轉移率臨界曲線
設定網格兵力的初始分布為均勻分布M=100,N=100,A,B,C三方和空格φ的比例大約為1∶1∶1∶1,交戰率μ和轉移率σ為可調參量,通過調整交戰率μ和轉移率σ,觀察斑圖的動態演化情況和各方的戰斗、擴散情況,并記錄在 15 000代時三方兵力的具體情況。
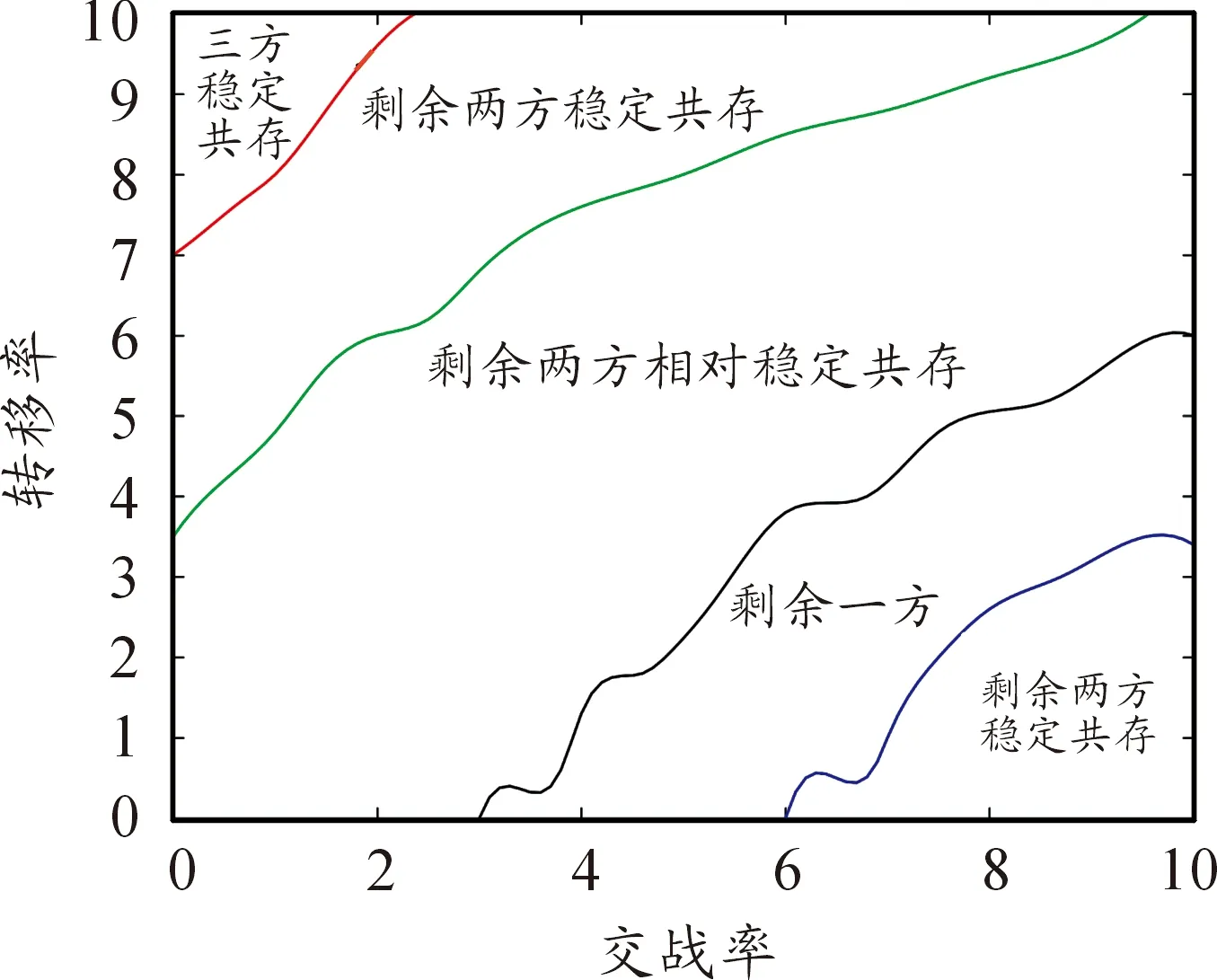
由于三方作戰與傳統作戰有一定的不同,在作戰結果方面會出現以下情況:(1)三方穩定共存,即在一定的時間內作戰三方都無法被消滅。(2)兩方相對穩定共存,即在一定的時間內剩余兩方但兩方的剩余兵力不等。(3)兩方穩定共存,即在一定的時間內剩余兩方且兩方剩余兵力相等。(4)僅存在一方。其中兩方相對穩定共存會隨著仿真的繼續會轉化為兩方共存且兵力相等情況或者僅存一方情況。
通過50次仿真模擬得到數據取均值后得出短距移動模式下交戰率—轉移率臨界曲線為圖4所示,由圖可知在交戰率μ≤1且轉移率σ≥9時三方共存,由于此時交戰率較低且轉移率較高,使得部隊更加趨于不同網格間的流動而不是不同兵力間的作戰,故在 15 000代時三方共存。
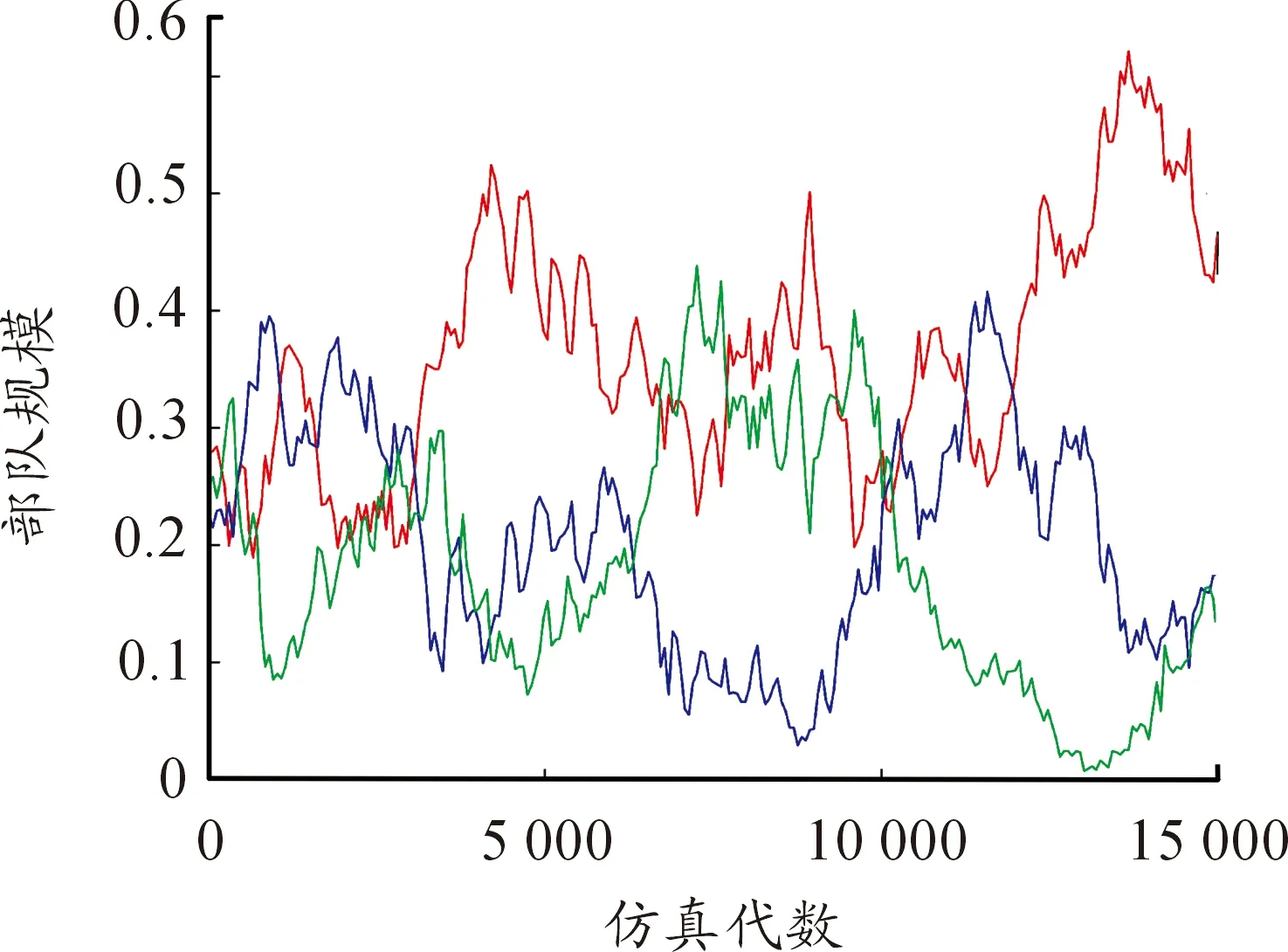
圖5為當μ=0.5,σ=9.5時三方兵力的密度時間曲線。從圖中可以看出,隨著時間的推移,三方的兵力出現此消彼長,交替性增長和衰減的情況,彼此間相互抗衡,說明此時三方形成了穩定共存狀態。
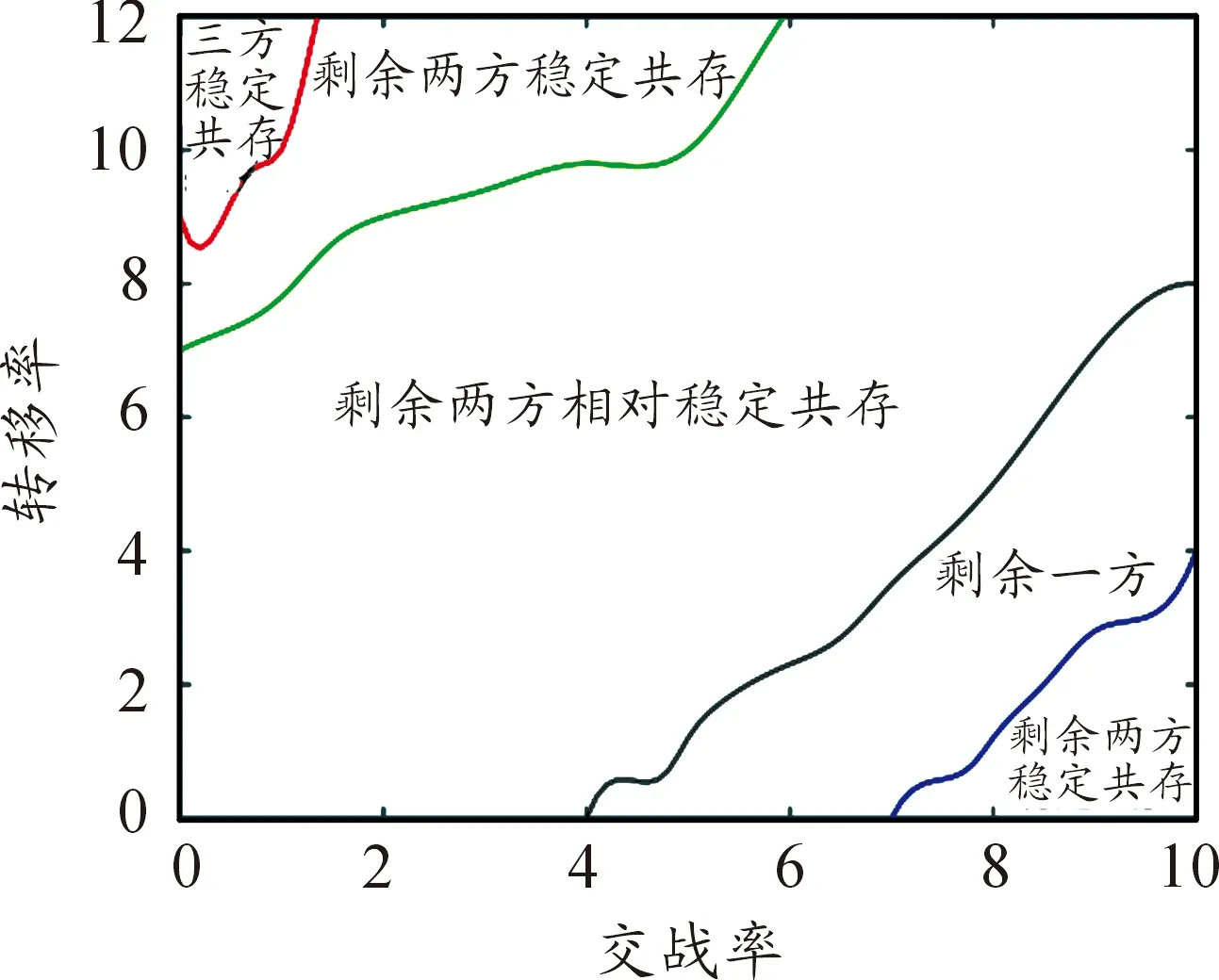
圖4 短距移動模式交戰率—轉移率臨界曲線
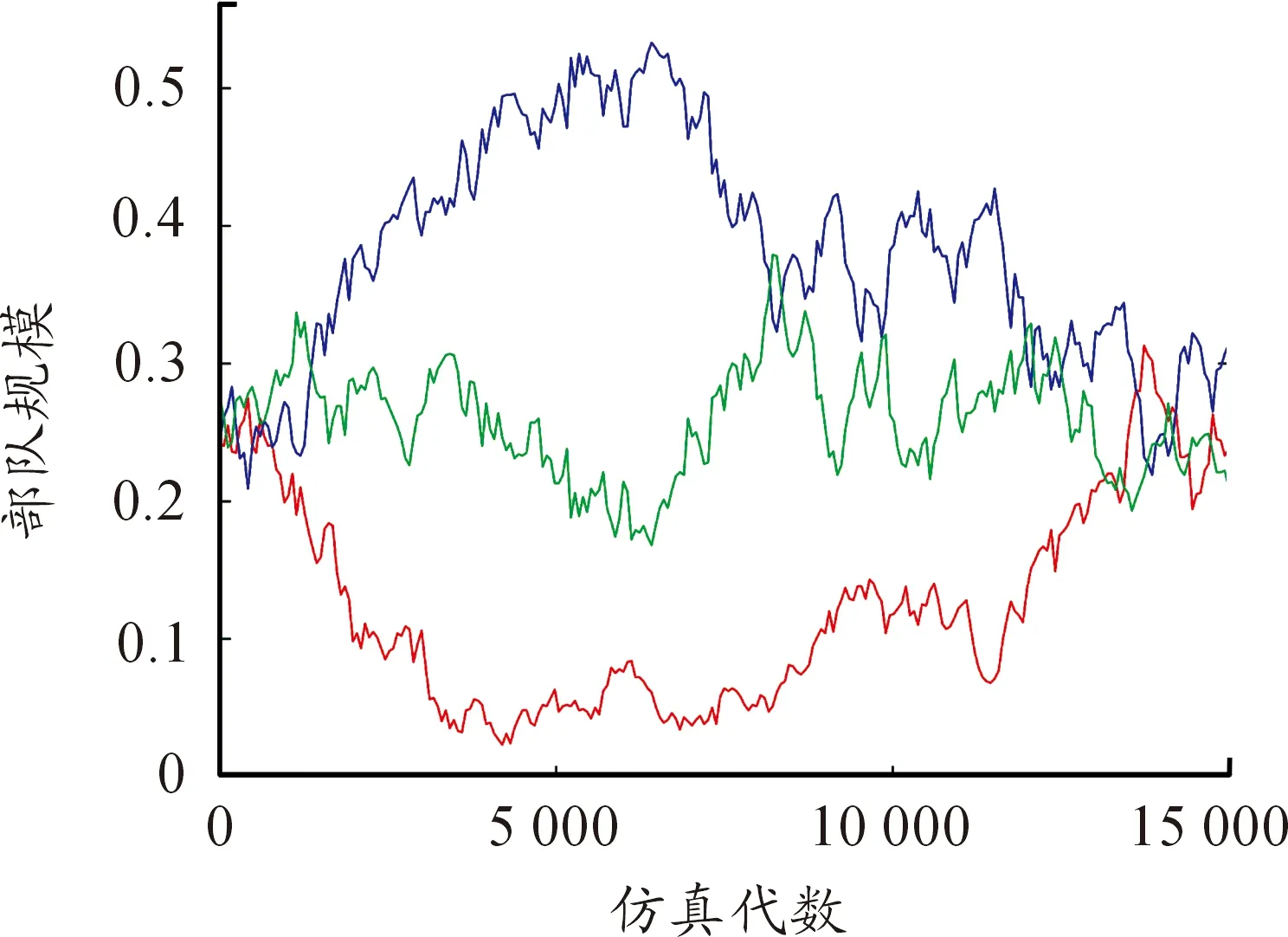
圖5 短距移動模式μ=0.5,σ=9.5密度時間曲線
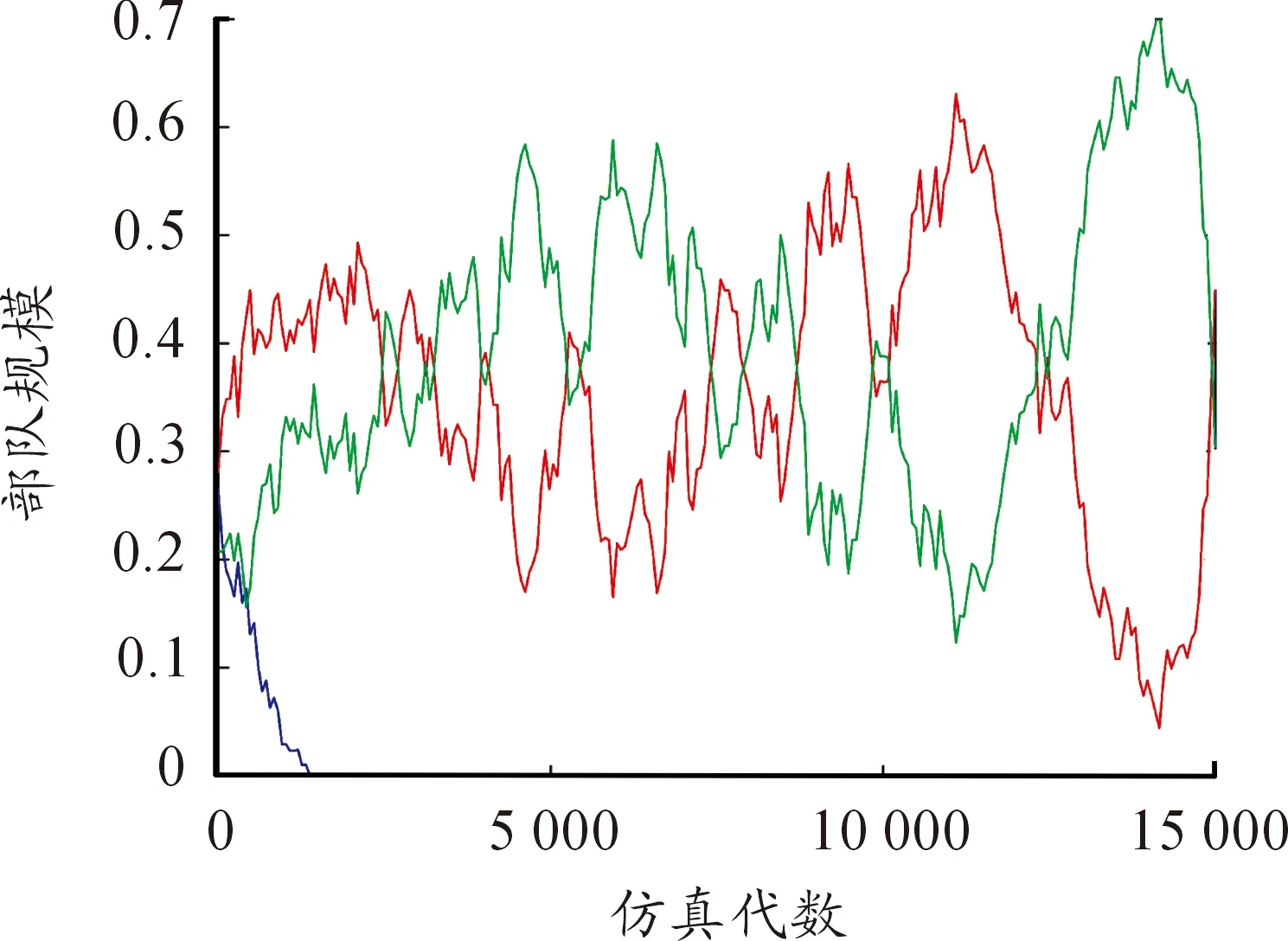
圖6為當μ=3,σ=7時三方兵力的密度時間曲線。從圖中可以看出,隨著時間的推移,在8 000代時一方已經被完全消滅,此時只剩余兩方,再經過時間的推移,剩余兩方的兵力出現交替性增長和衰減情況彼此間相互抗衡,說明此時為剩余兩方且穩定共存的狀態。
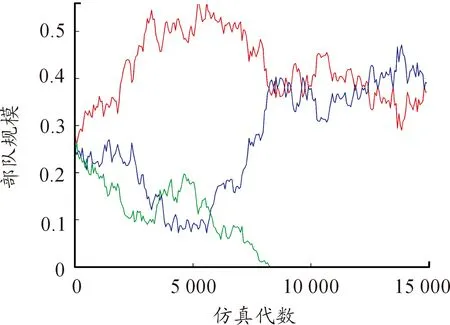
圖6 短距移動模式μ=3,σ=7密度時間曲線
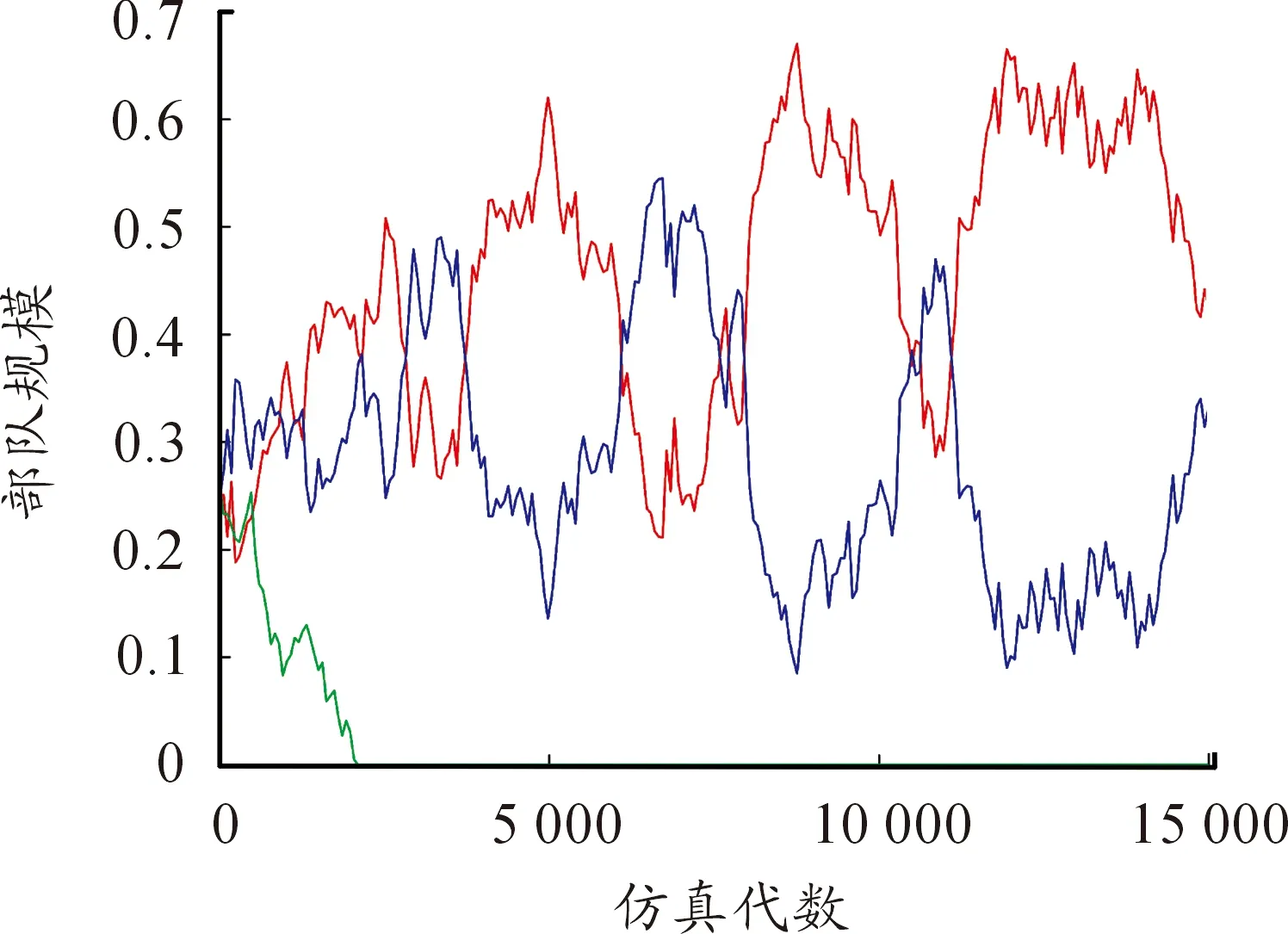
圖7為當μ=4,σ=4時三方兵力的密度時間曲線。從圖中可以看出,隨著時間的推移,在 14 000代時一方已經被完全消滅,此時只剩余兩方但兩方的兵力不相等,再經過時間的推移到仿真結束前,剩余兩方的兵力出現交替性增長和衰減情況彼此間保持相對平衡的狀態,此時為剩余兩方且相對穩定的狀態,對處于該狀態的兩方進行繼續仿真得到兩種狀態一種問為剩余兩方且穩定共存狀態另一種為剩余一方狀態。
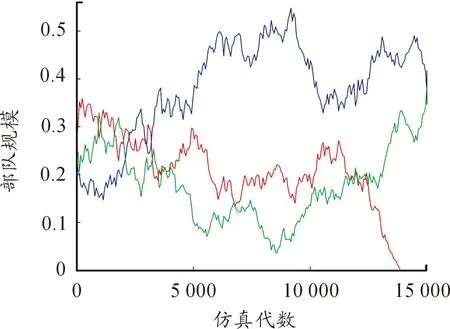
圖7 短距移動模式μ=4,σ=4密度時間曲線
圖8為當μ=7,σ=3三方兵力的密度時間曲線。從圖中可以看出,隨著時間的推移,在7 500代時一方已經被完全消滅,此時只剩余兩方但兩方的兵力不相等,在13 500代時另一方也被完全消滅,此時只剩余一方直到仿真結束。
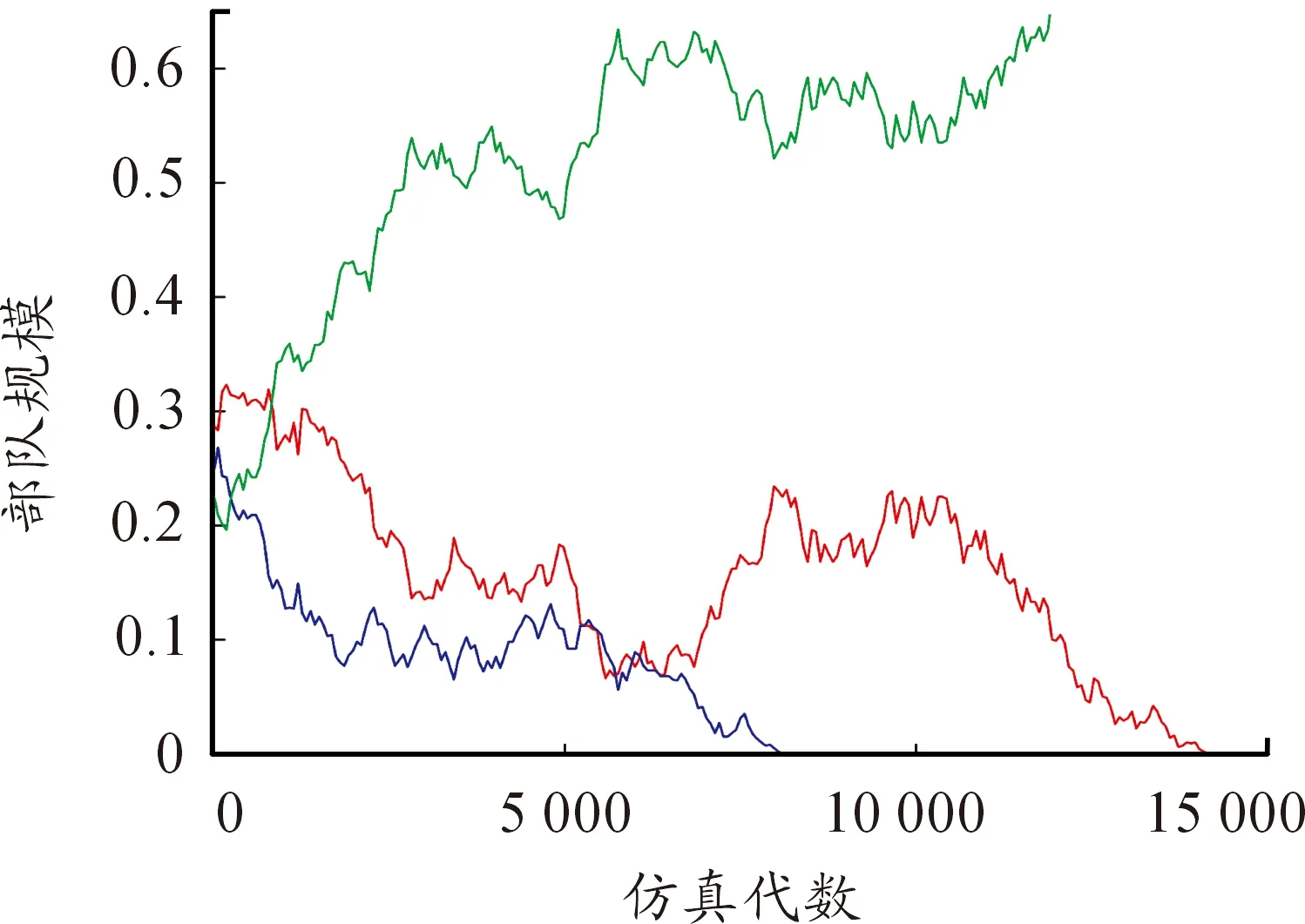
圖8 短距移動模式μ=7,σ=3密度時間曲線
1.3 交戰率μ對穩定斑圖的影響
依據短距移動模式三方Lanchester作戰模型,選擇三方穩定共存狀態研究交戰率μ對穩定斑圖的影響。取交戰率μ=0.5轉移率σ=11和交戰率μ=1.5轉移率σ=11兩種情況的穩定斑圖進行研究。根據多次實驗可知,在13 000代左右斑圖狀態為三方穩定共存狀態,13 000代和13 100代上述兩種情況的斑圖如圖9。
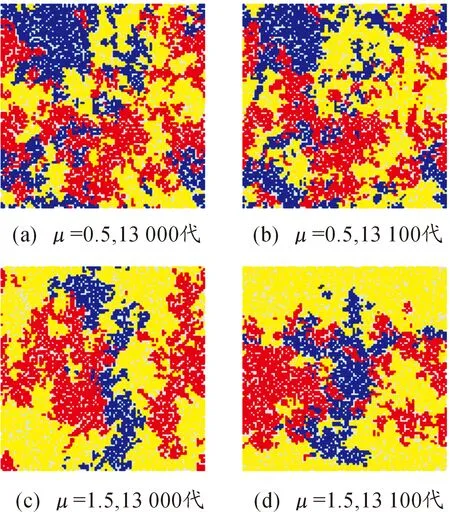
圖9 轉移率σ=11的斑圖
通過觀察圖9,當交戰率μ=0.5時,穩定斑圖中各個兵力分布較為分散,零散的斑塊較多但不集中,說明此時系統的自組織性較弱,而當交戰率μ=1.5時,穩定斑圖中出現了多個較大的斑塊,零散的斑塊較少,說明此時系統的自組織性較強。再選取不同的交戰率進行上述步驟觀察斑圖的演化結果與上述相同。故在不超出穩定狀態的臨界范圍的情況下,交戰率越大斑圖的斑塊越趨于集中,系統的自組織性越強。
1.4 轉移率σ對穩定斑圖的影響
依據短距移動模式三方Lanchester作戰模型,選擇三方穩定共存狀態研究轉移率σ對穩定斑圖的影響。取交戰率μ=1轉移率σ=8和交戰率μ=1轉移率σ=11兩種情況的穩定斑圖進行研究。根據多次實驗可知,在13000代左右斑圖狀態為三方穩定共存狀態,故取13 000代和13 100代上述兩種情況的斑圖如圖9、圖10。
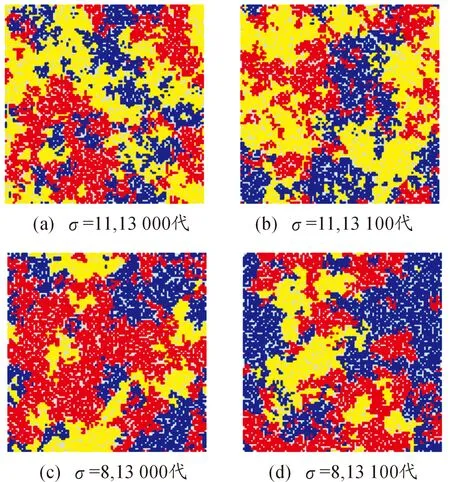
圖10 交戰率μ=1時的.斑圖
通過觀察圖10,當轉移率σ=8時,穩定斑圖中出現了多個較大的斑塊,零散的斑塊較少,說明此時系統的自組織性較強。而當轉移率σ=11時,穩定斑圖中各個兵力分布較為分散,零散的斑塊較多基本上沒有形成穩定的大斑塊,說明此時系統的自組織性較弱。再選取不同的交戰率進行上述步驟觀察斑圖的演化結果與上述相同。故在不超出穩定狀態的臨界范圍的情況下,轉移率越大斑圖的斑塊越趨于分散,斑塊間流動性越強,系統的自組織性越弱。
2 長距移動模式
2.1 Levy飛行
Levy飛行描述了由許多小步長和少量大步長組成的移動模式[19],在生物的搜索捕食行為中較為顯著。已有研究發現在海洋中的一些捕食者在大范圍搜捕食物過程中和野外蜜蜂回巢的過程甚至果蠅、麋鹿和信天翁等運動都存在Levy飛行方式[20,22]。Levy飛行是一種垂尾分布在大范圍空間的搜索捕食中,Levy飛行是一種比布朗運動更有效的搜索策略。在作戰中,使用Levy飛行策略對敵方目標進行搜索和攻擊可以縮短搜索進程提高搜索效率。
Levy飛行的運動距離的概率密度為冪率分布即:
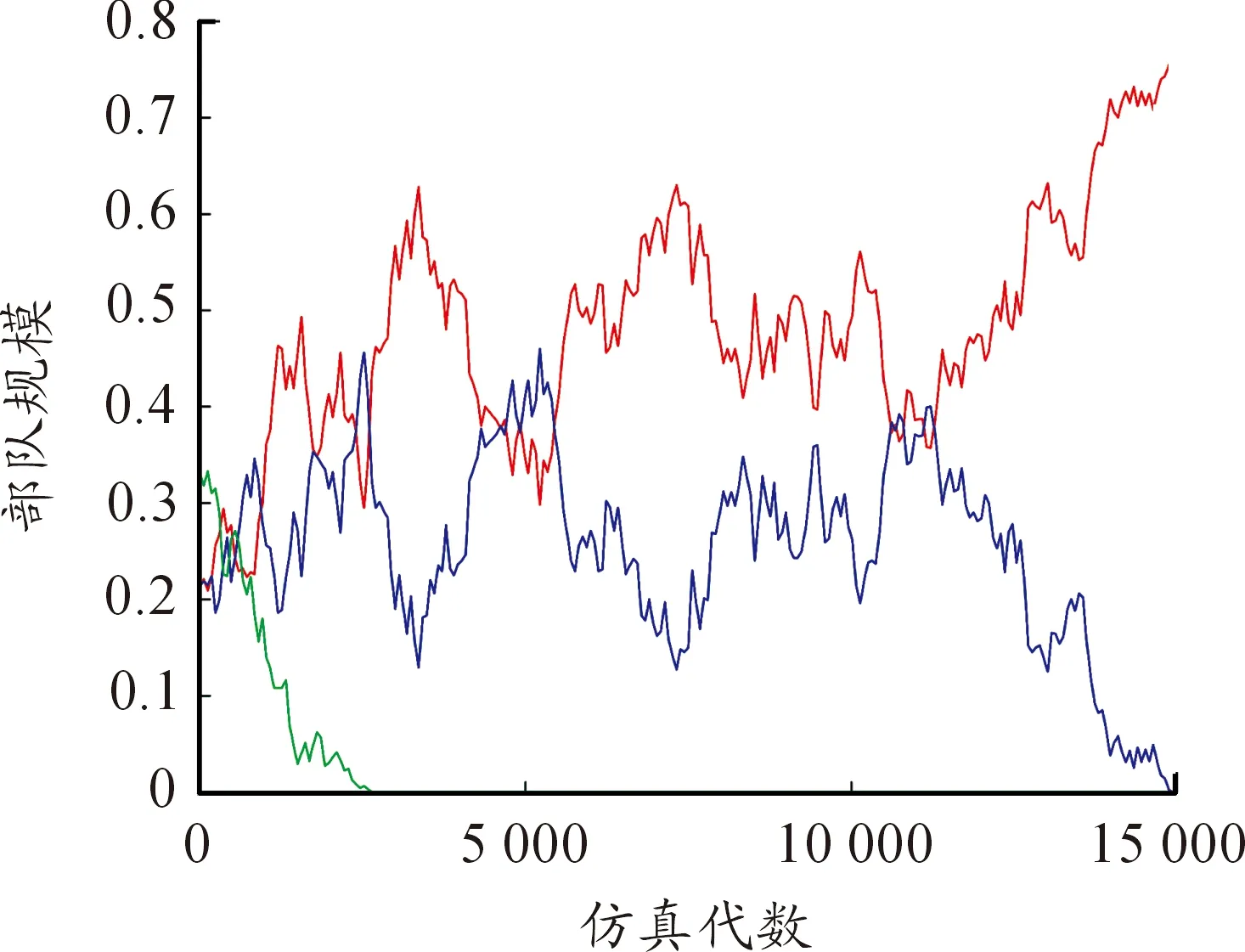
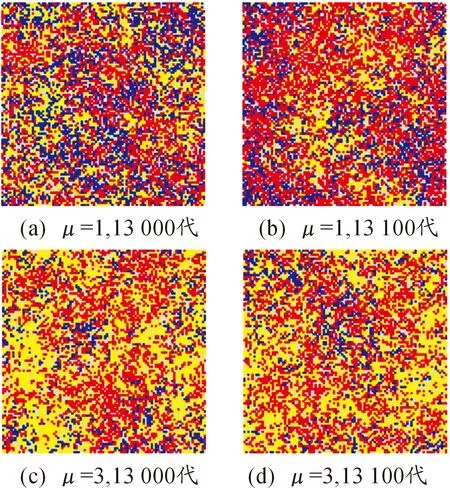
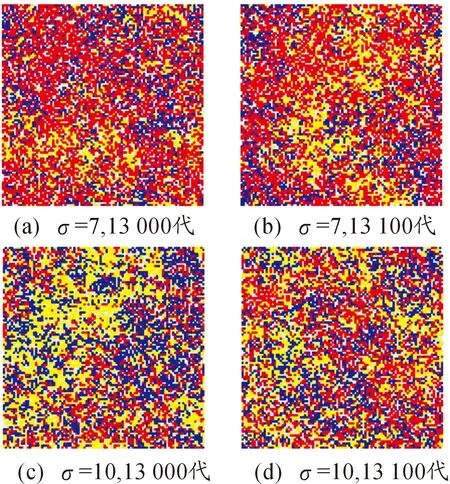
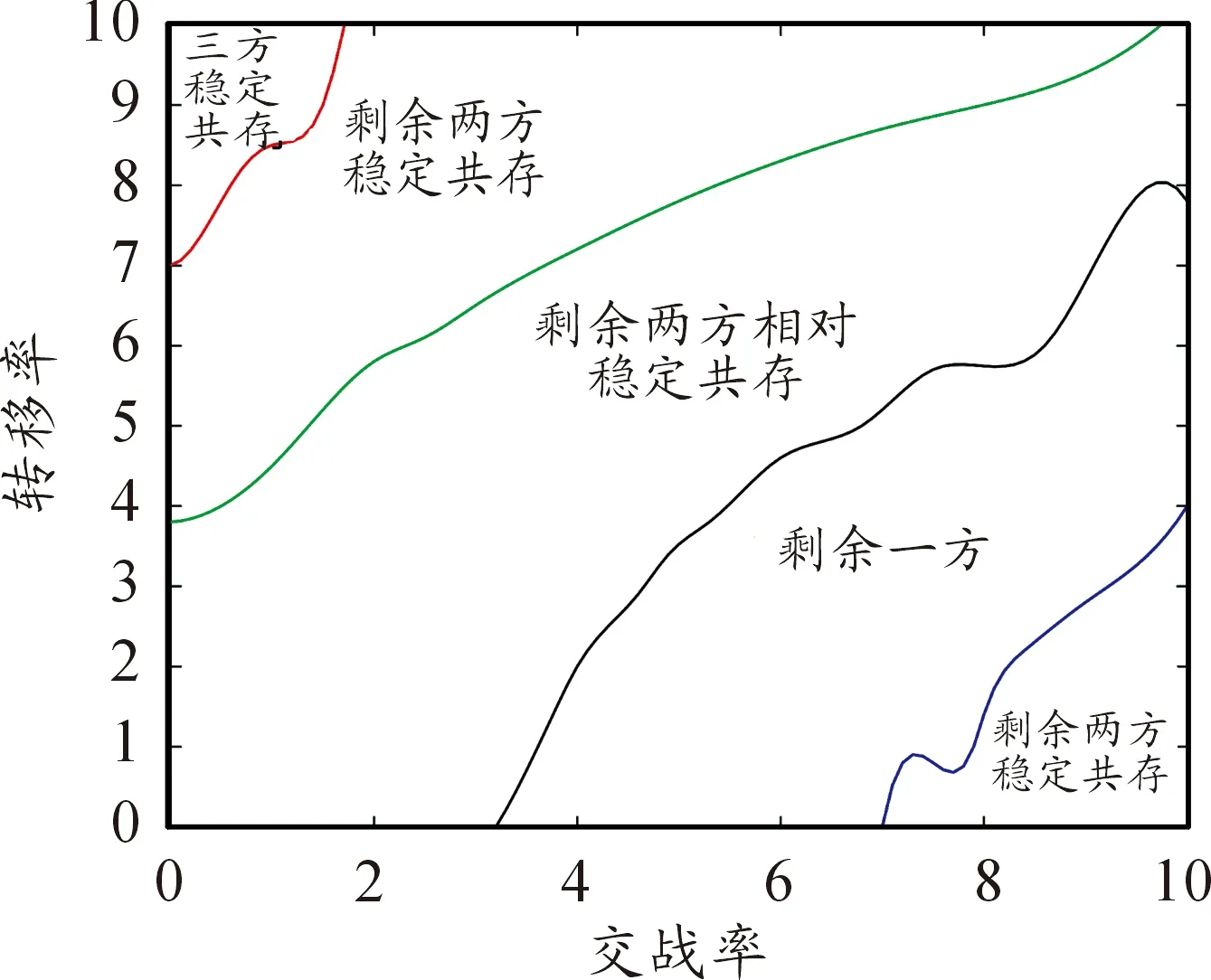
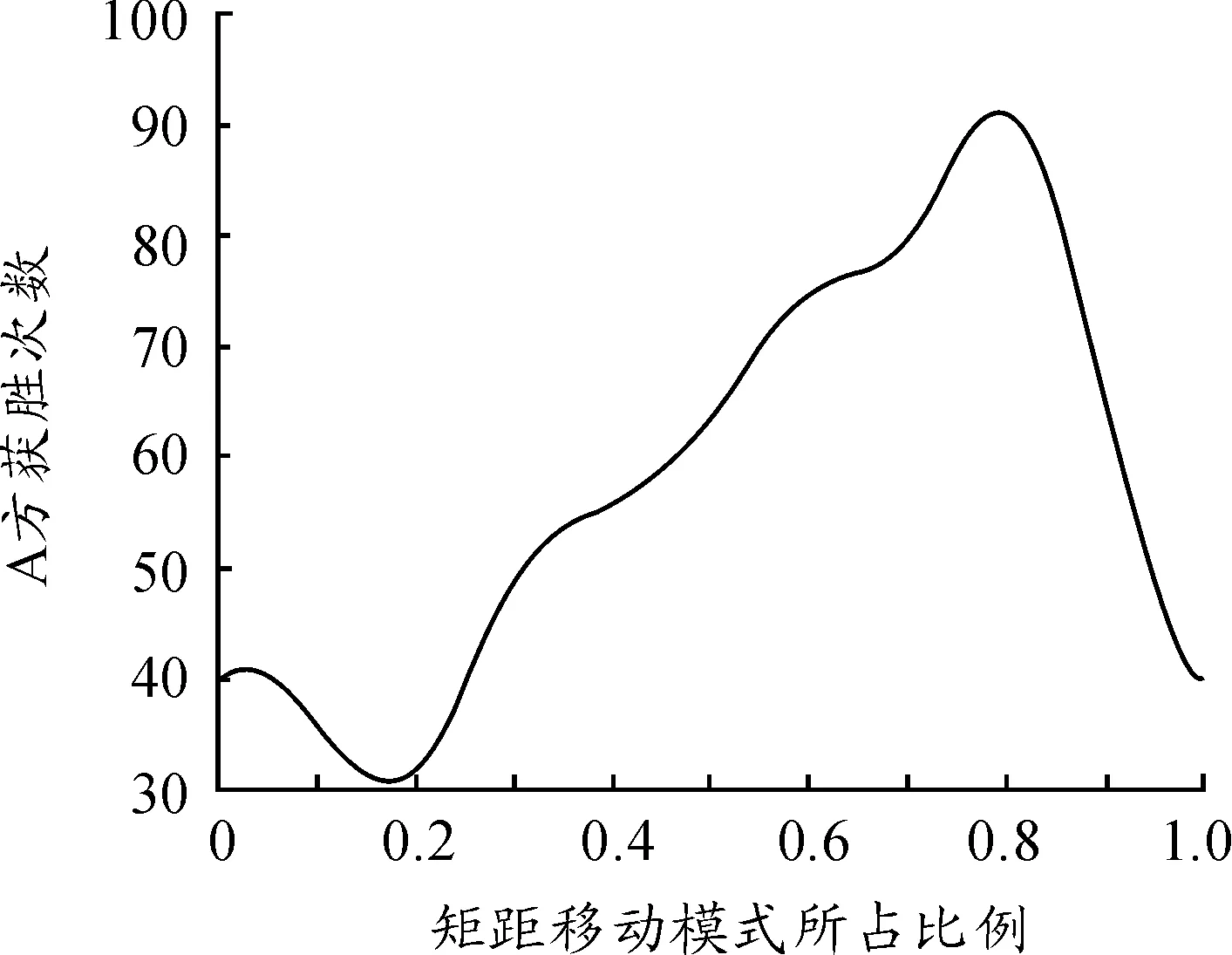
L(s)=C·s-h(1 (3) 式中,s為Levy飛行步長,s∈[s0,smax],s0為最小步長,smax為最大步長,C=(1-h)·s1-h,h為冪指數,經過研究發現,當h≈2時,為Levy飛行最優策略。 本文使用Mantegna算法[22]生成Levy飛行步長,如下所示: (4) 式中U、V滿足正態分布: (5) 標準差σU、σV滿足下式: (6) 式中,Γ(z)為gamma函數。 圖11為Levy飛行的飛行軌跡。 圖11 Levy飛行軌跡 采用與第一章相同的M×N平面網格,A,B,C三方和空格φ之間的相互作用與式(1)式(2)相同,采用蒙特卡洛隨機模擬方法,具體步驟如下: 步驟1:在整個網格中隨機選擇一個存在兵力的網格; 步驟2:使用蒙特卡洛方法確定下一個網格處于現在網格的方向;按照式(4)計算Levy飛行步長; 步驟3:根據計算的方向和步長確定網格與步驟1確定的網格,按照式(1)或者式(2)的反應方程進行反應; 步驟4:重復步驟1直至仿真結束。 取網格兵力的初始分布為均勻分布M=100,N=100,A,B,C三方和空格φ的比例大約為1∶1∶1∶1,Levy飛行參數β=2,s0=2,smax=20。交戰率μ和轉移率σ為可調參量,通過調整交戰率μ和轉移率σ,觀察斑圖的動態演化情況和各方的戰斗、擴散情況,并記錄在15 000代時三方兵力的具體情況。 通過50次仿真模擬得到數據取均值后得出短距移動模式下交戰率—轉移率臨界曲線為圖12所示,通過觀察并與圖4作對比發現,長距移動模式下各個狀態的臨界曲線與短距模式下有較大不同,在相同交戰率情況下長距移動模式三方穩定共存的情況相對于短距移動模式轉移率較低,同時長距移動模式下出現兩方相對穩定共存的情況的在圖中所占面積與短距相比較小。與短距移動模式相比,在長距移動模式下,兩方穩定共存狀態的所占面積較大。由于Levy飛行使得系統中斑塊間的流動性增大,故相對減少了系統的自組織性,為了保持和原系統相似的狀態,需在同等條件下增大交戰率或者減少轉移率以增大系統的自組織性或減少斑塊間的流動性。 圖12 長距移動模式交戰率—轉移率臨界曲線 圖13為當μ=0.5,σ=8時三方兵力的密度時間曲線,隨著時間的推移,三方的兵力出現此消彼長情況,彼此間相互抗衡,說明此時三方形成了穩定共存狀態。圖14為當μ=3,σ=6時三方兵力的密度時間曲線。從圖中可以看出,隨著時間的推移,在1 000代時一方已經被完全消滅,此時只剩余兩方,之后剩余兩方的兵力彼此間相互抗衡,說明此時為剩余兩方且穩定共存的狀態。 圖13 長距移動模式μ=0.5,σ=8密度時間曲線 圖15為當μ=5,σ=5時三方兵力的密度時間曲線,隨著時間的推移,在2 000代時一方已經被完全消滅,此時只剩余兩方但兩方的兵力不相等,再經過時間的推移到仿真結束前,剩余兩方的兵力出現交替性增長和衰減情況彼此間保持相對平衡的狀態,此時為剩余兩方且相對穩定的狀態,對處于該狀態的兩方進行繼續仿真得到兩種狀態一種為剩余兩方且穩定共存狀態另一種為剩余一方狀態。 圖14 長距移動模式μ=3,σ=6密度時間曲線 圖16為當μ=6,σ=3三方兵力的密度時間曲線,隨著時間的推移,在2 000代時一方已經被完全消滅,此時只剩余兩方但兩方的兵力不相等,在15 000代時另一方也被完全消滅,此時只剩余一方直到仿真結束。 圖15 長距移動模式μ=5,σ=5密度時間曲線 圖16 長距移動模式μ=6,σ=3密度時間曲線 依據長距移動模式三方Lanchester作戰模型,選擇三方穩定共存狀態研究交戰率μ對穩定斑圖的影響。取交戰率μ=1轉移率σ=10和交戰率μ=3轉移率σ=10兩種情況的穩定斑圖進行研究。根據多次實驗可知,在10 000代左右斑圖狀態為三方穩定共存狀態,故取10 000代和10 100代上述兩種情況的斑圖如圖17。 圖17 轉移率σ=10的斑圖 通過觀察圖17,在第10 000代時斑圖中有一些較大的斑塊中存在一些較小的斑塊,而在10 100代時這些小的斑塊將大斑塊侵蝕消滅,這是由于Levy飛行增加了不同網格間兵力的流動,使得在短距狀態下無法發生的交戰在長距狀態下便可以發生,故大斑塊會被小斑塊消滅。當交戰率μ=1時,穩定斑圖中各個兵力分布較為分散,零散的斑塊較多且不集中,說明此時系統的自組織性較弱,而當交戰率μ=3時,穩定斑圖中出現了多個較大的斑塊,零散的斑塊較少,說明此時系統的自組織性較強。再選取不同的交戰率進行上述步驟觀察斑圖的演化結果與上述相同。故在不超出穩定狀態的臨界范圍的情況下,交戰率越大斑圖的斑塊越趨于集中,系統的自組織性越強。 據短距移動模式三方Lanchester作戰模型,選擇三方穩定共存狀態研究轉移率σ對穩定斑圖的影響。取交戰率μ=0.5轉移率σ=7和交戰率μ=0.5轉移率σ=10兩種情況的穩定斑圖進行研究。根據多次實驗可知,在10 000代左右斑圖狀態為三方穩定共存狀態,故取10 000代和10 100代上述兩種情況的斑圖如圖18。 圖18 交戰率μ=0.5時的斑圖 通過觀察圖18,當轉移率σ=10時,穩定斑圖中各個兵力分布較為分散,零散的斑塊較多基本上沒有形成穩定的大斑塊,說明此時系統的自組織性較弱。而當轉移率σ=7時,穩定斑圖中出現了多個較大的斑塊,說明此時網格間部隊流動減少系統的自組織性較強。再選取不同的交戰率進行上述步驟觀察斑圖的演化結果與上述相同。故在不超出穩定狀態的臨界范圍的情況下,轉移率越大斑圖的斑塊越趨于分散,網格間部隊流動性越強,系統的自組織性越弱。 采用與第一章相同的平面網格,三方和空格之間的相互作用與式(1)式(2)相同,部隊的移動模式不僅僅為短距或者Levy飛行,先采用蒙特卡洛隨機模擬方法確定網格的具體移動模式,在進行斑塊間的反應,具體步驟如下: 步驟1:在整個網格中隨機選擇一個存在兵力的網格; 步驟2:采用蒙特卡洛隨機模擬方法確定網格的具體的移動模式; 步驟3:若移動模式為Levy飛行模式,使用蒙特卡洛方法確定下一個網格處于現在網格的方向;按照式(4)計算Levy飛行步長;若移動模式為短距移動模式則判別已經選擇的網格的上下左右四個方向的網格狀態; 步驟4:若移動模式Levy飛行模式為根據計算的方向和步長確定網格與步驟1確定的網格按照式(1)或者式(2)的反應方程進行反應;若移動模式為短距移動模式則隨機選擇一個方向的網格按照式(1)或者式(2)的反應方程進行反應; 步驟5:重復步驟1直至仿真結束。 取網格兵力的初始分布為均勻分布,三方和空格的比例大約為,Levy飛行參數。短距移動模式選擇概率為交戰率和轉移率為可調參量,通過調整交戰率和轉移率,觀察斑圖的動態演化情況和各方的戰斗、擴散情況,并記錄在15 000代時三方兵力的具體情況。 通過50次仿真模擬得到數據取均值后得出短距移動模式下交戰率—轉移率臨界曲線為圖19所示,通過觀察并與圖4、圖12作對比發現,在混合移動移動模式下各個狀態的臨界曲線與短距和長距模式下有較大不同,在相同交戰率情況下混合移動模式三方穩定共存的情況相對于短距移動模式轉移率較低而基本上與長距移動模式相同,混合移動模式下出現兩方相對穩定共存的情況的在圖中所占面積與其他兩種移動模式相比較小,而兩方穩定共存狀態的所占面積較大。由于Levy飛行使得系統中斑塊間的流動性增大,故相對減少了系統的自組織性,但由于混合移動模式下網格間的移動為Levy飛行模式和短距模式共同作用,使得系統的自組織性減少的同時,通過這種混合移動模式使得系統的穩定性得到增加,故穩定共存的面積得到了增加。 圖19 混合移動模式交戰率—轉移率臨界曲線 依據混合移動模式三方Lanchester作戰模型,選擇三方穩定共存狀態研究交戰率μ對穩定斑圖的影響。取交戰率μ=0.5轉移率σ=9和交戰率μ=1.5轉移率σ=9兩種情況的穩定斑圖進行研究。根據多次實驗可知,在12 000代左右斑圖狀態為三方穩定共存狀態,故取12 000代和12 100代上述兩種情況的斑圖如圖20。 圖20 轉移率σ=9時的斑圖 通過觀察圖20,當交戰率μ=0.5時,斑圖中各個兵力較為分散,但也有少量的同種兵力聚集的斑塊,并且12 000代和12 100代的斑圖差別較大,說明此時系統的自組織性較差不同網格間兵力的流動性較強。當交戰率μ=1.5時,在 12 000代時斑圖中出現了較大的同種兵力聚集的斑塊,在這些斑塊附近也分散著一些零散的斑塊,在12 100代時斑圖中一些斑塊被消滅分散但也出現了一些新的同種兵力聚集的較大斑塊,說明此時系統有一定的自組織性并且不同網格間兵力的流動性也較強。再選取不同的交戰率進行上述步驟觀察斑圖的演化結果與上述相同。故在不超出穩定狀態的臨界范圍的情況下,交戰率越大斑圖的斑塊越趨于集中,系統的自組織性越強。 據混合移動模式三方Lanchester作戰模型,選擇三方穩定共存狀態研究轉移率μ對穩定斑圖的影響。取交戰率μ=1轉移率σ=8和交戰率μ=1轉移率σ=11兩種情況的穩定斑圖進行研究。根據多次實驗可知,在12 000代左右斑圖狀態為三方穩定共存狀態,故取12 000代和12 100代上述兩種情況的斑圖如圖21。 圖21 交戰率μ=1時的斑圖 通過觀察圖21,當轉移率σ=11時,斑圖中各個兵力較為分散并且12 000代和12 100代的斑圖差別較大,說明此時系統的自組織性較差不同網格間兵力的流動性較強。當轉移率σ=8時,在12 000代時斑圖中出現了較大的同種兵力聚集的斑塊,在這些斑塊附近也分散著一些零散的斑塊,在12 100代時斑圖中一些斑塊被消滅分散但也出現了一些新的同種兵力聚集的較大斑塊,說明此時系統有一定的自組織性并且不同網格間兵力的流動性也較強。再選取不同的交戰率進行上述步驟觀察斑圖的演化結果與上述相同。故在不超出穩定狀態的臨界范圍的情況下,轉移越大斑圖的斑塊越趨于分散,網格間不同兵力的流動性越強。 由3.2節可知,Ps為在實際仿真中選擇短距移動模式的概率,即移動模式為短距移動模式部隊在整個部隊中所占比值。部隊參加作戰最終的目的應為消滅敵人,保存自己,所以應選擇三方作戰最終只剩一方的情況進行分析。在三方兵力中選擇A方使用混合移動模式其兵力用紅色表示,其余兩方兵力用黃色和藍色表示,空格φ用灰色表示三方的兵力比為A,B,C三方和空格φ的比例大約為1∶1∶1∶1,Levy飛行參數β=2,s0=2,smax=20,μ=5,σ=1,ps為可調變量。分三種情況,其余兩方皆為短距移動模式,其余兩方皆為長距移動模式和一方為短距移動模式一方為長距移動模式。調節ps,并在每一個值進行100次仿真A方獲勝次數繪制曲線圖如圖22~圖24所示。 圖22 其余方為短距移動模式A方獲勝次數曲線 圖23 其余方為長距移動模式A方獲勝次數曲線 圖24 其余方一方為長距移動模式一方為短距移動模式A方獲勝次數曲線 通過圖22~圖24可知當ps=0.8時即短距移動模式和長距移動模式部隊的比值為4∶1時,紅方獲勝次數最多,同時可知,當A方僅有短距移動模式時,部隊的獲勝次數最少,而增加了長距移動模式的兵力后獲勝次數增加,當短距移動模式和長距移動模式部隊的比值小于1∶1時,部隊的獲勝次數開始下降。由于Levy飛行增加了部隊的自由度和攻擊半徑,使得其在對抗中可以攻擊到短距移動模式下無法攻擊的部隊,同時當長距移動模式比值過大時由于增加了部隊的自由度使得部隊不易聚集在一起反而會使得部隊容易被攻擊故在不斷增加長程移動模式兵力后會使得部隊的獲勝次數下降。 1) 本文提出了交戰率μ和轉移率σ為影響作戰過程的變量,通過仿真得到在不同模型下的交戰率—轉移率臨界曲線,確定了不同穩定狀態下交戰率和轉移率的取值范圍。 2) 交戰率的增大會增強系統的同種兵力間聚合能力,使斑塊增大,增強系統的自組織性。轉移率的增加會加速不同網格間兵力的移動,加速系統的流動性。 3) 加入Levy飛行移動模式后,系統的流動性得到加強,同一種狀態的臨界曲線上的交戰率取值增大,轉移率取值減少。 4) 混合移動模式下短距移動模式部隊和長距移動模式部隊的最佳比值為4∶1。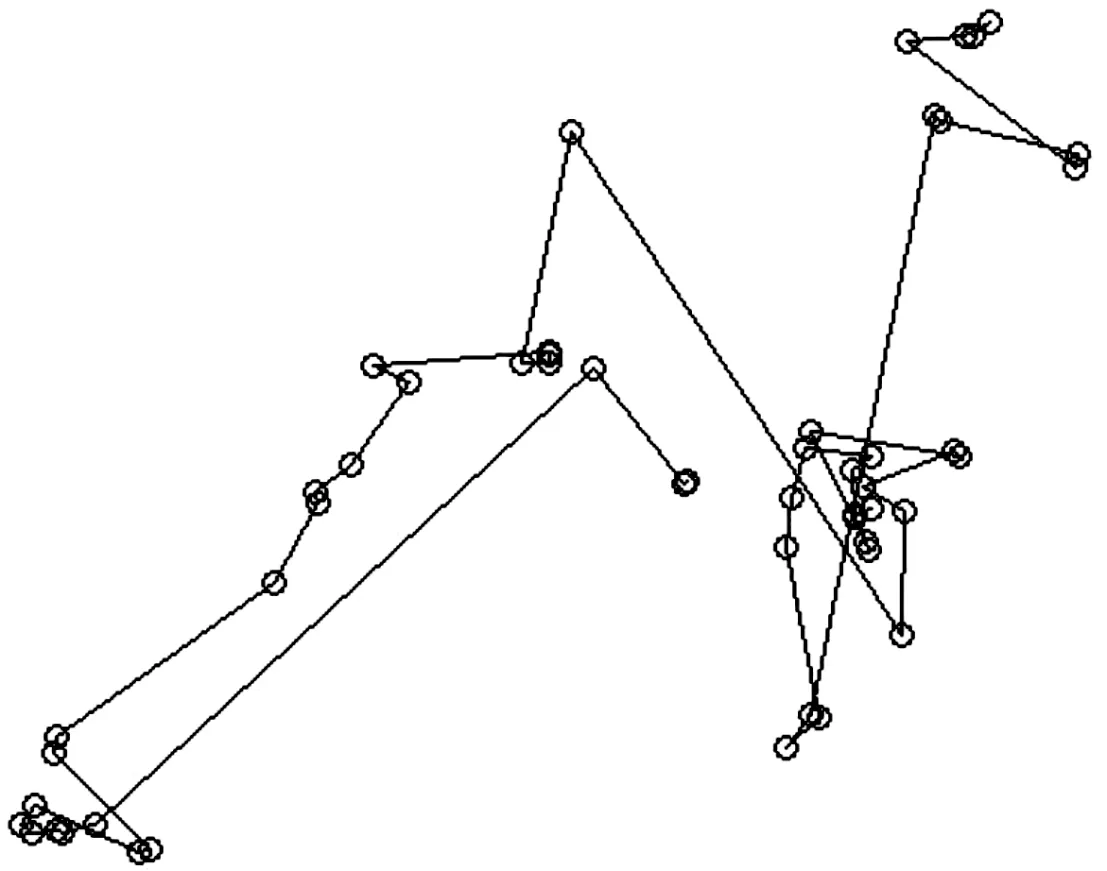
2.2 長距移動模式三方Lanchester作戰模型
2.3 交戰率μ對穩定斑圖的影響
2.4 轉移率σ對穩定斑圖的影響
3 混合移動模式
3.1 混合移動模式三方Lanchester作戰模型
3.2 交戰率—轉移率臨界曲線
3.3 交戰率μ對穩定斑圖的影響
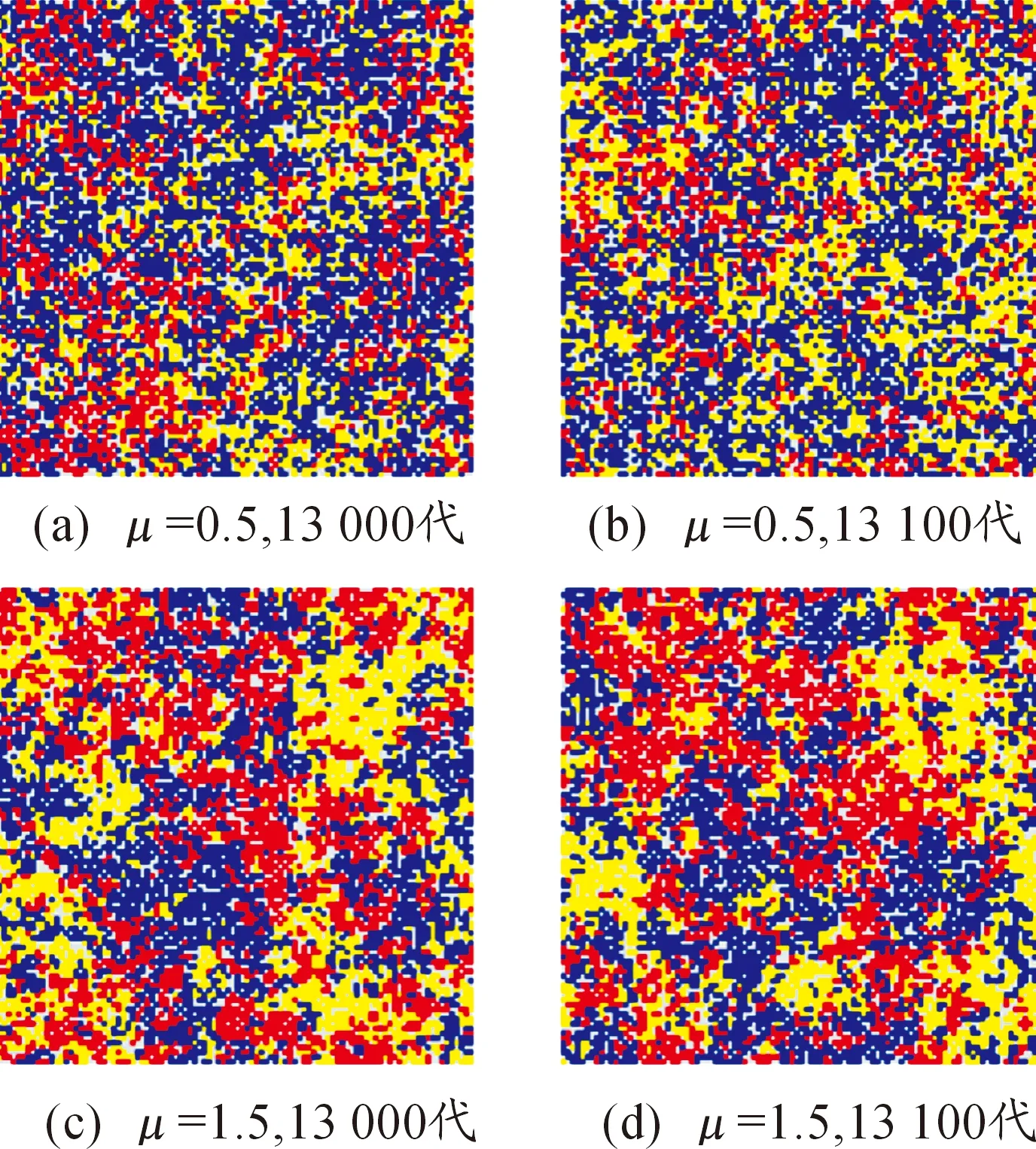
3.4 轉移率σ對穩定斑圖的影響
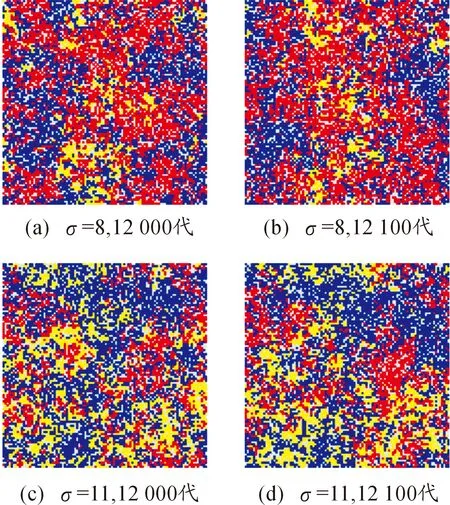
3.5 短距移動模式與長距移動模式最佳部隊比值
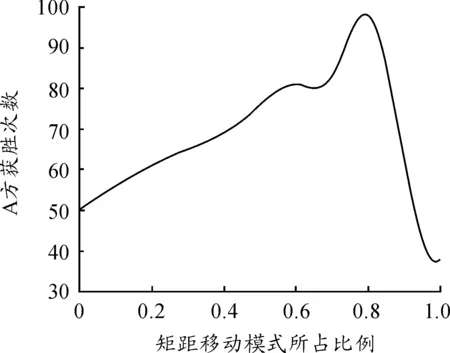
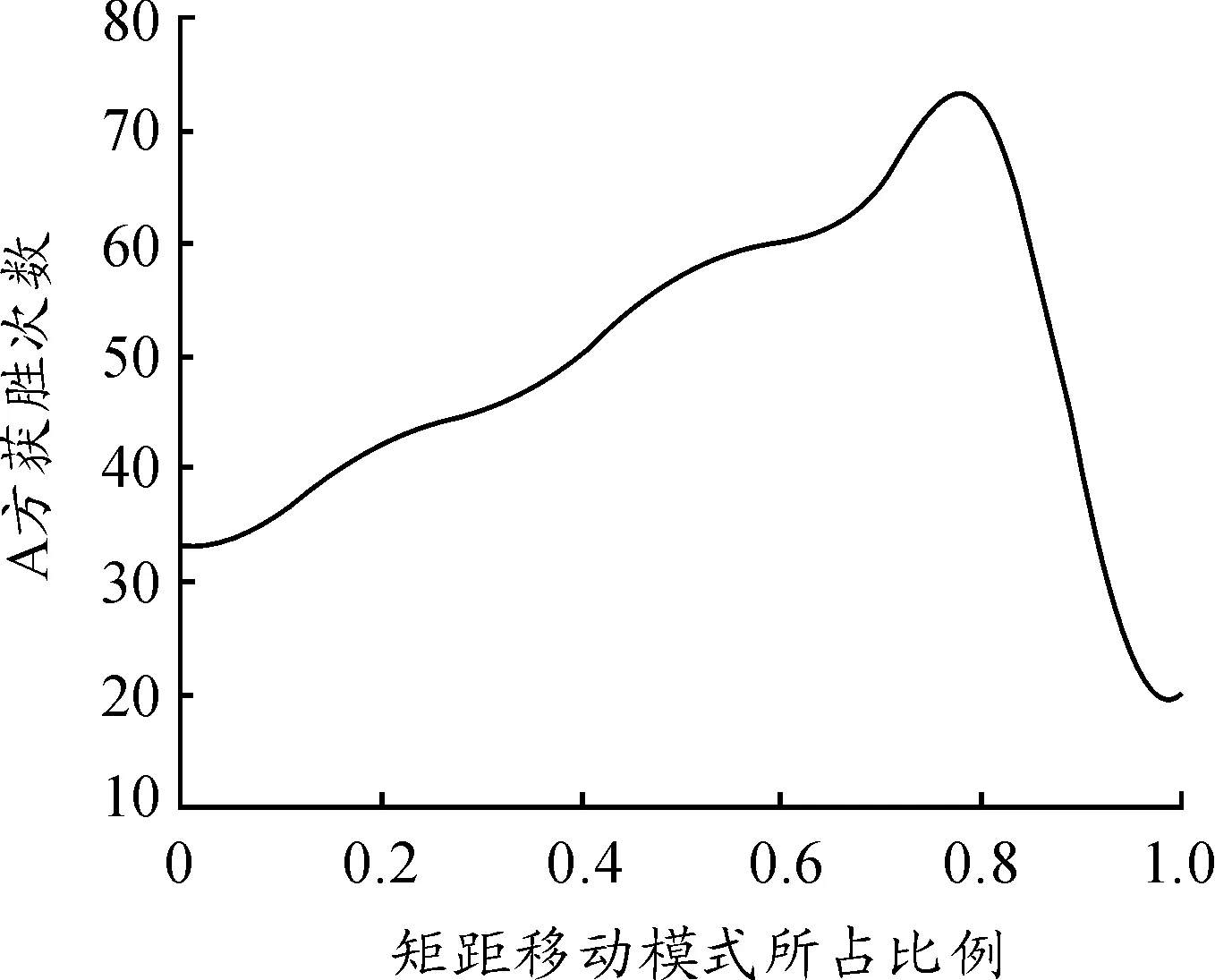
4 結論

