預警機支援下的地空導彈殺傷區遠界研究
吳小鶴,李彥寬,代進進,唐嘉鈺
(1.海軍航空大學, 山東 煙臺 246001; 2.煙臺北方星空自控科技有限公司, 山東 煙臺 264003)
隨著國際軍事形勢不斷激化,我國領海面臨的威脅也越來越嚴峻。加之現代武器的發展和空襲戰術的多樣化,在要地防空和島礁防御中,對抗低空超低空目標的作戰能力需求迫在眉睫。根據目標防區外發射、低空飛行等特點,單平臺單火力的防御作戰模式無法滿足作戰需求,結合地空導彈的防御性能,在預警機深度探測的支援下,能夠使得地空導彈性能擴大化。由于在預警機支援下單平臺的地空導彈系統實現了解耦,因此傳統單平臺導彈射擊諸元計算方法不再適用這一新的作戰形式。針對這一類問題,諸多學者從空艦協同、艦艦協同等方面對導彈殺傷區進行了進一步分析,而針對空地協同的殺傷區研究比較欠缺。文獻[1]討論了艦艦協同在編隊防空中艦空導彈殺傷區問題,從殺傷區配置和不同縱深進行了建模分析。文獻[2]指出艦載直升機與艦空導彈協同下目標航路捷徑可增加150%。文獻[3]實現了動態火力下多平臺組網,使得地空導彈在合理部署火力單元位置情況下擴展了殺傷區遠界,各項射擊諸元得到了相應的提高。文獻[4]對預警機引導編隊協同作戰進行了仿真分析,可供實際作戰參考。本文以一體化防空作戰體系和預警機協同下中遠程地空導彈反導作戰過程為背景,基于等角航線[5]的目標模型,構建殺傷區坐標模型,分析影響預警機支援下地空導彈殺傷區遠界因素,給出殺傷區遠界點的計算方法。
1 坐標系及目標模型
1.1 單平臺殺傷區
在評估一個防空導彈武器系統時導彈的殺傷區是一項最重要的指標之一,它能夠直觀地體現武器系統的綜合作戰性能,其決定了導彈應具備的射程、高度和航路捷徑[6]。殺傷區即指地空導彈武器系統以不低于某一給定概率殺傷空中目標的導彈與目標遭遇的空間范圍[7]。顯然地,在殺傷區空域內各點導彈殺傷目標的概率并不一致,但必然不低于一個最低定值。地空導彈殺傷區的形狀和大小取決于導彈自身的物理特性、目標運動特性及戰場環境。
就平臺武器系統而言,傳統假設目標做等速直線運動迎面空襲我方目標,以地面直角坐標系為基準構建迎區殺傷區,殺傷區空間形狀如圖1所示。
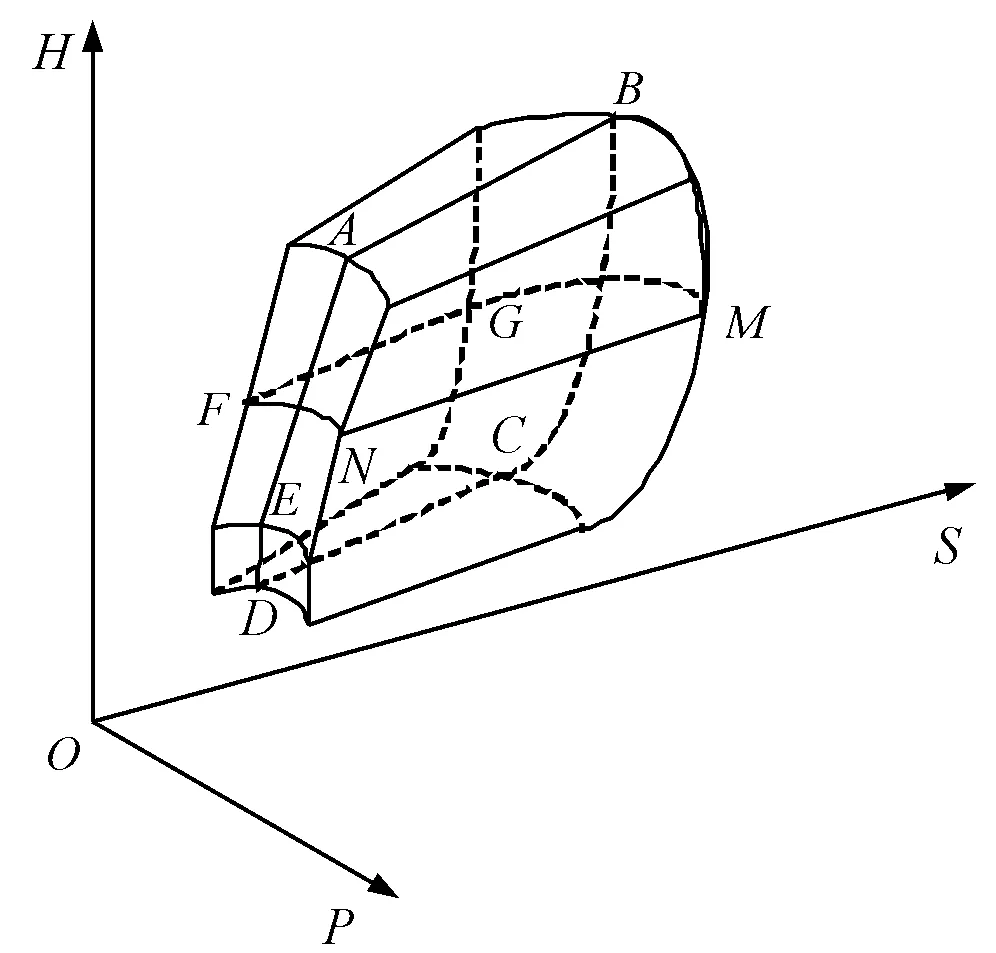
圖1 單平臺地空導彈殺傷區空間形狀
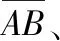
1.2 地空協同殺傷區坐標
在現代戰爭中,目標空襲多采取防區外發射,近距離時采取低空超低空突防。為此必然要重點考慮到地球曲率對攔截目標的影響,傳統簡單的認為目標做等速直線運動顯然不符合實際戰場環境。因此,根據地球曲率的特點和實際分析情況,可以視目標在距離地面某一高度進行等角航線運動,即目標保持某一航向,且運動軌跡在地球表面的投影同各子午線的夾角相等[8]。基于目標等角航線運動構建的協同殺傷區坐標系如圖2所示,該方法避免了傳統坐標系隨目標運動而變化,更適用于當前戰場環境。
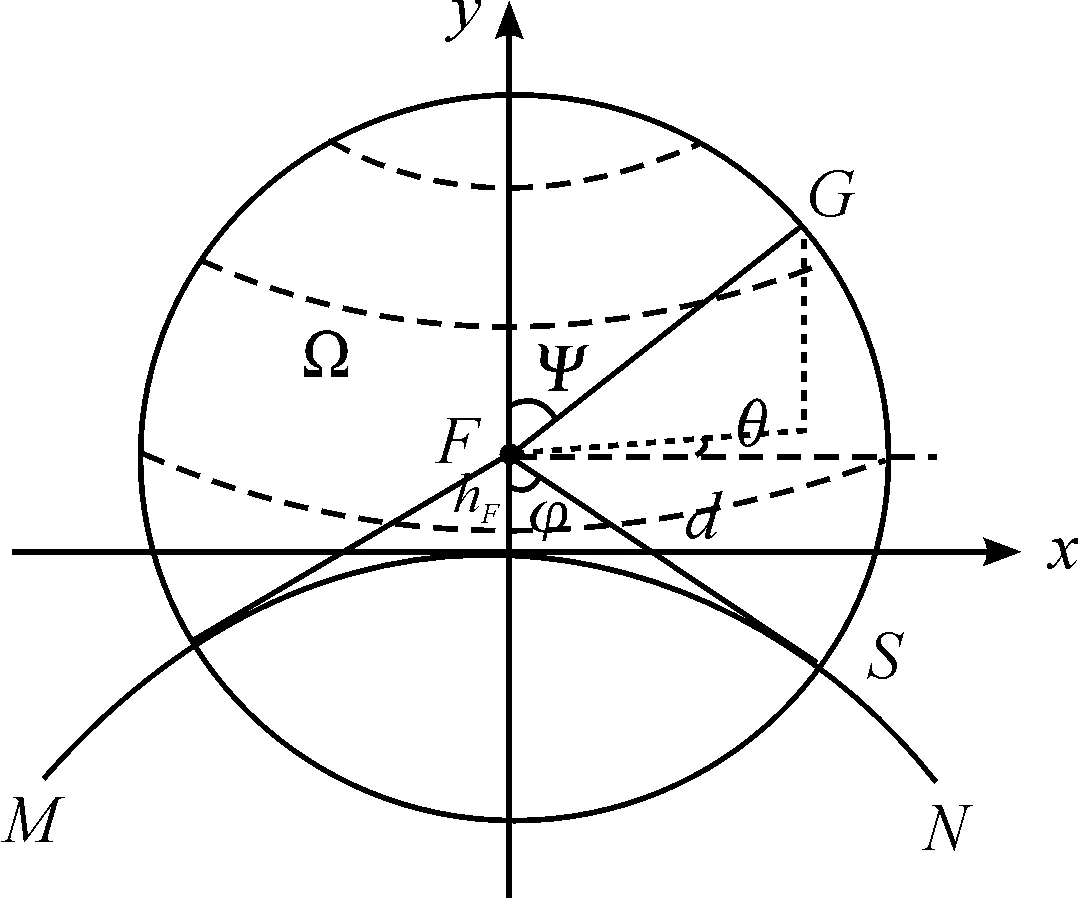
圖2中假設目標在地球表面上運動時等高等角航線,在地心坐標系OdXdYdZd之上,以地空導彈系統火力單元為原點O,Ox軸平行于水平面,且北偏東β角為正方向,Oy軸沿地球半徑方向垂直向上,由右手定則確定Oz軸。
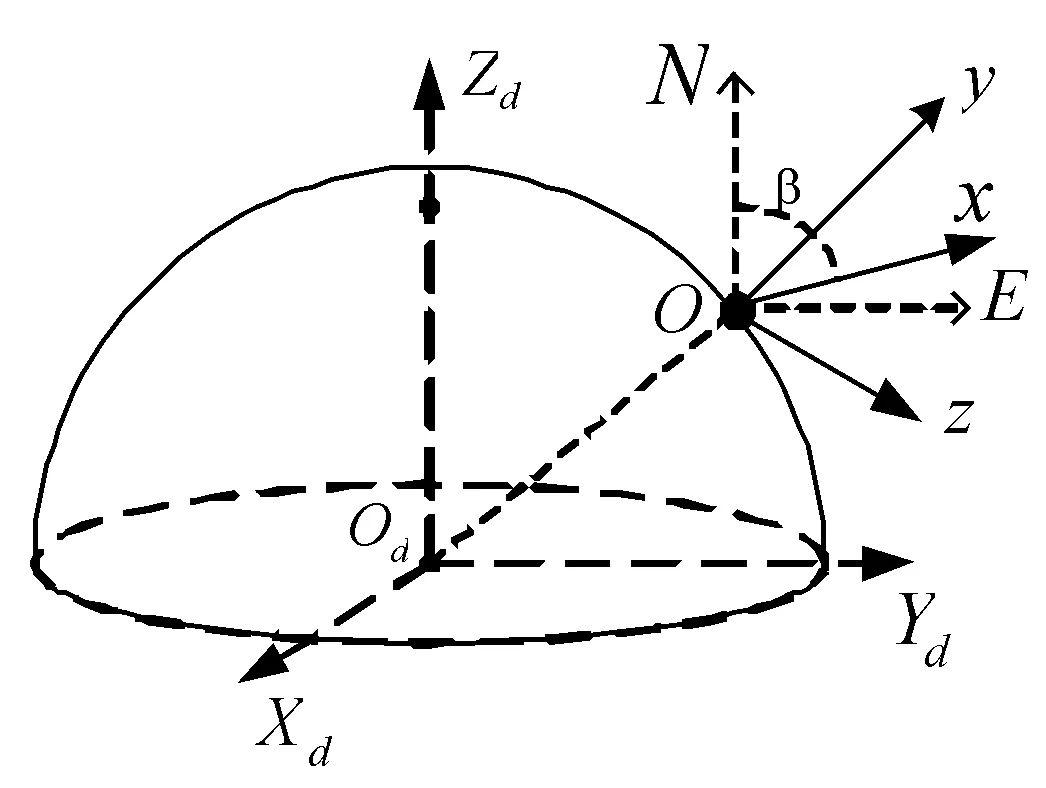
圖2 協同殺傷區坐標系
1.3 目標等角航線運動模型
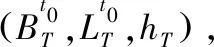
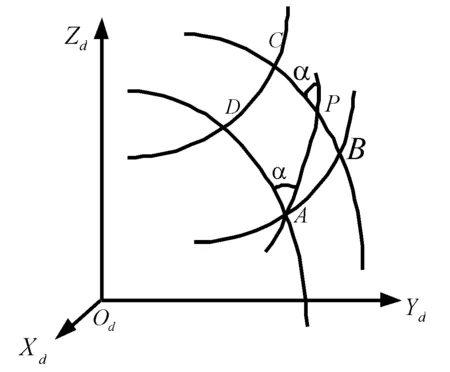
圖3 目標等角航線運動微分三角形
其中,ABCD所在的弧線為經緯線,AP為目標運動等角航線。在微分三角形ABP中,有微分量AP=ds,AB=NcosBdL,BP=MdB,且有微分方程為:
cosαds=MdB
(1)
sinαds=NcosBdL
(2)
(3)
方程中的M為子午線曲率半徑,N為卯酉圈曲率半徑。假設目標在AP段等角航線運動時間為s,經過對微分方程式(1)-式(3)的計算分析,可得:
LTts+1-LTts= tanα(qP-qA)
qP= arctanh(sinBTts+1)-earctanh(esinBTts+1)
qA= arctanh(sinBTts)-earctanh(esinBTts)
e為地球的第一偏心率。點P的緯度可根據文獻[5]的子午線弧長反解公式直接求出,即:
其中φ、ai(i=2,4,6,8)的取值可參考文獻[5]。
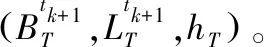
2 協同殺傷區的計算方法
在預警機支援下地空導彈超視距攔截低空超低空目標作戰過程中,根據作戰任務和預警機引導模式,預警機參與導彈從準備到命中的全過程。因此,殺傷區必然隨著預警機的介入而發生變化,殺傷區實質是彈目遭遇點的空間集合,影響殺傷區的主要因素有導彈最大飛行斜距、雷達制導跟蹤距離等。地空導彈在預警機協同制導下能夠擺脫地面雷達的限制,而預警機的介入也使得地球曲率造成的影響很小甚至可以忽略。此時殺傷區的變化主要是跟蹤制導能力得到了進一步加強,殺傷區遠界也隨之發生變化。
2.1 跟蹤探測能力
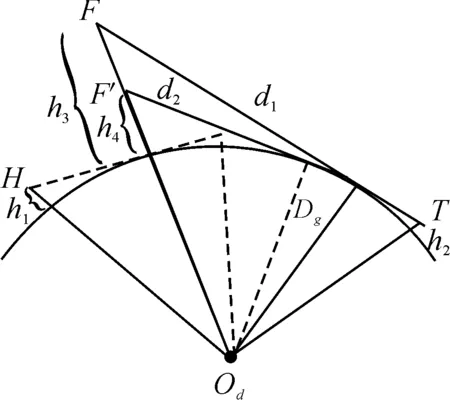
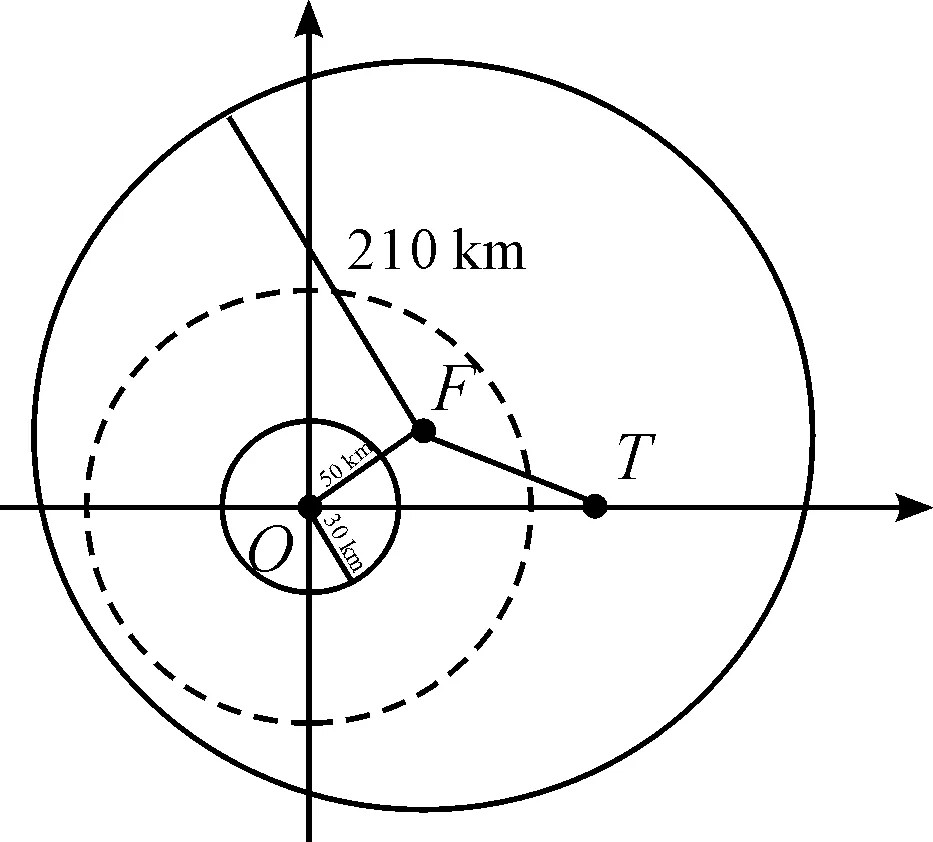
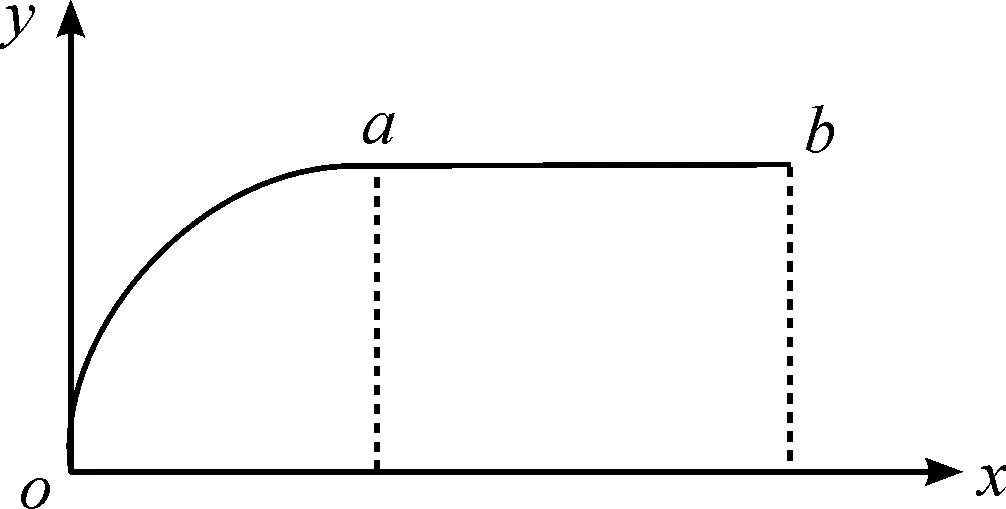
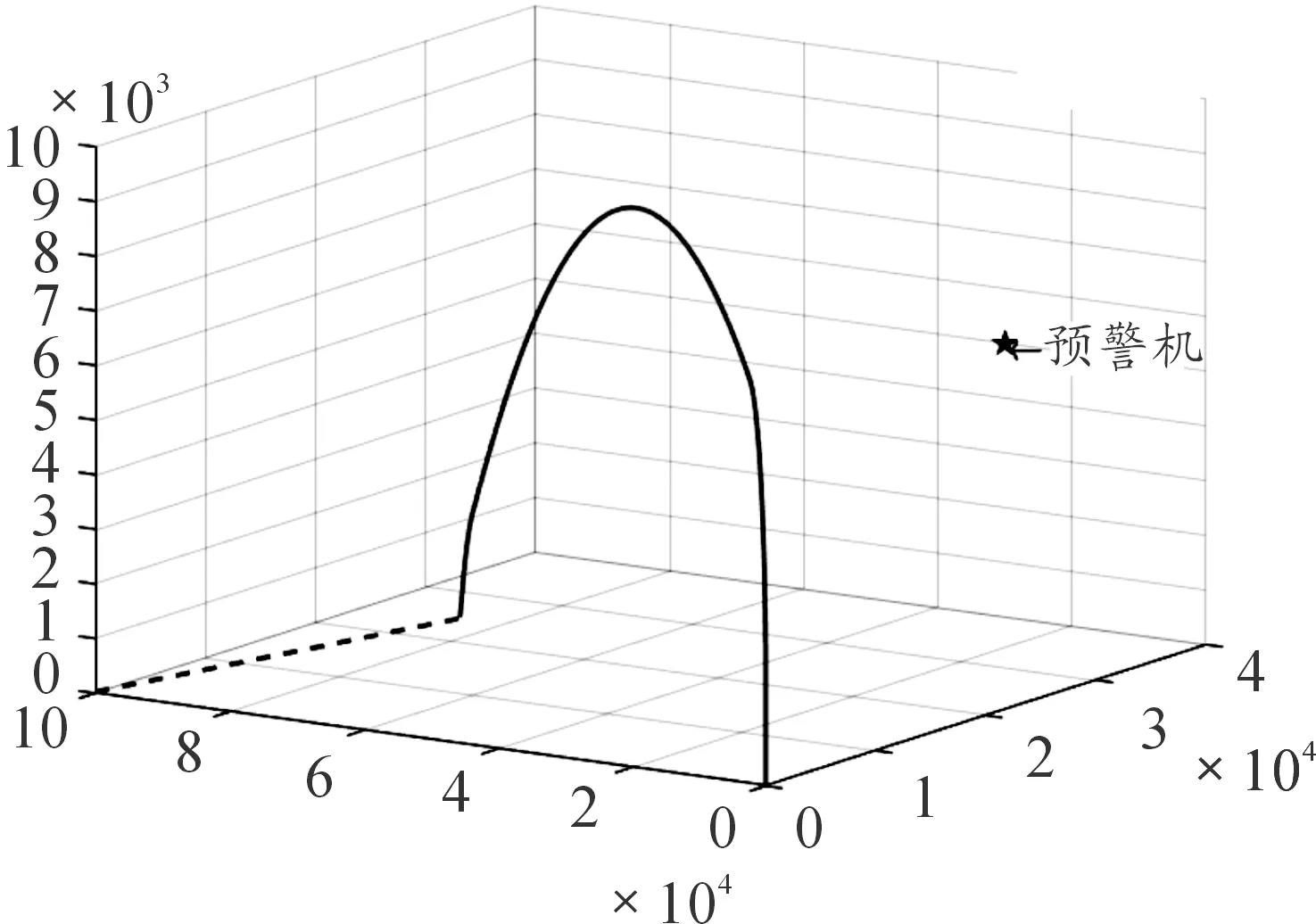
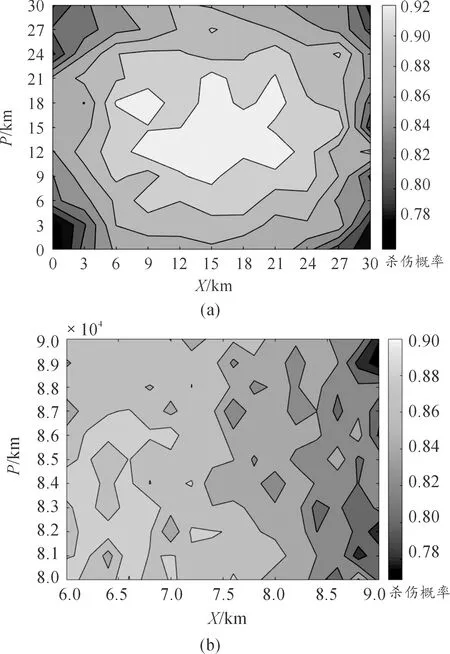
預警機和地空導彈武器系統組成的作戰單元,可以滿足超視距作戰任務的需求。由于雷達在不同高度所達到的最大作用距離不同,因此有必要先對預警機位置進行分析。假設地空導彈武器系統為一個點,即發射車和雷達車之間的距離忽略不計,則各平臺在水平面上的位置關系如圖4所示。火力圈以導彈發射點為中心,半徑為導彈最大射程DH;雷達圈以地面武器系統雷達車為中心,半徑為雷達最大作用距離DL。預警機圈以預警機在水平面的投影為中心,半徑為機載雷達最大作用距離DY。3個范圍圈的大小關系是DL 圖4 水平面位置關系 垂直平面上預警機、導彈武器系統和目標在地心坐標系上的位置關系如圖5所示。其中H為導彈發射位置,高度h1;T為目標位置,高度h2;F(F′)為預警機位置,飛行高度h3(h4);地球半徑為De。明顯地,地球曲率的存在產生了雷達盲區,而雷達直視距離可表示為[10] 圖5 垂直面位置關系 圖6 跟蹤探測作用范圍 在雷達跟蹤探測范圍足夠大或者不考慮雷達作用距離的情況下,殺傷區主要受導彈最大飛行斜距限制。最大飛行斜距與導彈性能參數有關,主要涉及最大飛行時間和發動機工作時間,兩種時間的計算可通過導彈彈道解算得到。根據彈道解算得到導彈速度變化曲線,對速度曲線在時間上進行積分運算即可求得導彈的斜射程,再對不同高度的彈道進行計算,即可得到相應的斜射程與高度的關系曲線,最后考慮最大飛行斜距的限制,就能夠得到在斜距限制下的殺傷區遠界。 殺傷區遠界的確定首先要明確是哪個因素對計算產生了限制,主要是預警機支援下跟蹤探測范圍限制和導彈最大飛行斜距限制。若跟蹤探測范圍空間大于導彈飛行距離,則殺傷區遠界受最大飛行斜距限制,相反地,殺傷區遠界由跟蹤探測范圍主導。根據預警機支援下導彈超視距攔截低空超低空目標的作戰任務和目的,通過兵力部署和陣地配置實現預警機支援下的跟蹤探測范圍足夠大,使得殺傷區遠界受導彈最大飛行斜距限制。假設現有某型地空導彈武器系統,導彈彈道解算模型已知,且目標參數由預警機確定,各項初始條件均已知,具體殺傷區遠界計算步驟如下: 步驟2:根據戰場環境、任務需求,針對目標特性確定預警機高度和前出距離,計算跟蹤探測空間Ω。 步驟3:若導彈到達步驟1確定的遠界點時目標飛出范圍Ω,則導彈無法命中目標,回到步驟1。否則執行步驟4。 步驟4:確定導彈發射時刻,預警機穩定跟蹤目標并制導導彈飛行,彈目最終遭遇點為殺傷區遠界。重復步驟1。 在導彈最大飛行斜距限制下,通過不同的目標特性分析和預警機配置得到一系列殺傷區遠界點,并組合成殺傷區遠界曲面。 參數假定:設某地空導彈發射陣地位于東經116.8°,北緯23°,海拔高度100 m。以該陣地為坐標原點,假設陣地的跟蹤制導雷達位置與發射陣地相同,雷達最大跟蹤制導距離為30 km,地空導彈平均速度970 m/s,最大速度1 700 m/s;目標(以巡航導彈為例)等角航線運動的航向角為120°,低空飛行速度為300 m/s,目標初始位置經緯高為(118°,23°,25),雷達截面積σ=0.2 m2;預警機前出發射陣地50 km,初始經緯高為(117°,23.3°,5 000),機載雷達直視距離300 km,根據目標特性機載雷達的跟蹤制導距離假設為直視距離的0.7倍,即210 km,則預警機不僅能夠探測并制導發射陣地的導彈,還能探測跟蹤遠程低空目標,三者之間的位置關系示意圖如圖7。 圖7 位置關系示意圖 根據不同高度彈道仿真的結果簡化出地空導彈飛行斜距隨目標高度變化曲線如圖8所示,橫軸為目標飛行高度,縱軸為最大飛行斜距。曲線oa為低空飛行段斜距的變化,a點高度6.5 km,ab高空段斜距不變,為110 km,b點高度為30 km。 圖8 最大飛行斜距隨目標高度變化曲線 設定總的反應時間為15 s,導彈最大過載為25 g,重力加速度g=9.8 m/s2,比例導引系數k=5,通過彈道仿真得到導彈與目標飛行軌跡如圖9所示。 圖9 導彈與目標飛行軌跡 目標飛行高度為25 m時,單平臺發射陣地雷達圈DL最遠跟蹤點在Oxyz坐標系下的坐標為(27 464.03, 7 827.87, 9 309.43),其限制的殺傷區遠界點坐標為L(22 430.02, 6 393.06, 9 122.38);預警機的跟蹤探測范圍遠超過發射陣地雷達跟蹤制導范圍和武器系統最大火力范圍,則在預警機支援下殺傷區受制于武器系統的最大火力范圍,即導彈最大飛行斜距,坐標為(85 710.12, 24 429.34, 55.57),對應遠界點斜距為89.12 km,如圖10所示。顯然,殺傷區遠界在預警機的支援下的得到了較大的擴展,算例中殺傷區遠界較單平臺約擴展了3.5倍。 圖10 殺傷區遠界 分別對單平臺和協同條件下采用蒙特卡洛方法進行50次抽樣實驗,實驗裝訂了預警機雷達制導誤差、系統誤差標準差及隨機誤差,得到水平殺傷區等高殺傷概率分布,如圖11所示。其中,圖11(a)表示的是單平臺水平殺傷區等高殺傷概率分布,可以得出單平臺下殺傷區遠界30 km左右,與彈道仿真結果相符;圖11(b)表示的是預警機協同下水平殺傷區等高殺傷概率分布,可以得出協同條件下殺傷區遠界在90 km左右,與彈道仿真結果相符。兩者相比,明顯地協同條件下遠界得到了較大擴展。 圖11 水平殺傷區等高殺傷概率分布 1) 通過對單平臺殺傷區的分析,考慮實際地理環境影響,建立了等角航向目標運動模型,并構建了協同下殺傷區坐標系。 2) 為消除地球曲率的影響對預警機的位置進行了配置,并配合導彈發射平臺到了探測跟蹤范圍的空間范圍。 3) 分析了在預警機支援下影響殺傷區遠界的因素,得出了在預警機飛行高度足夠高,探測跟蹤范圍足夠大的情況下殺傷區主要受到導彈最大飛行斜距限制。 4) 算例表明:預警機的支援使得導彈殺傷區遠界得到了成倍的擴展,導彈射程得到了有效的發揮。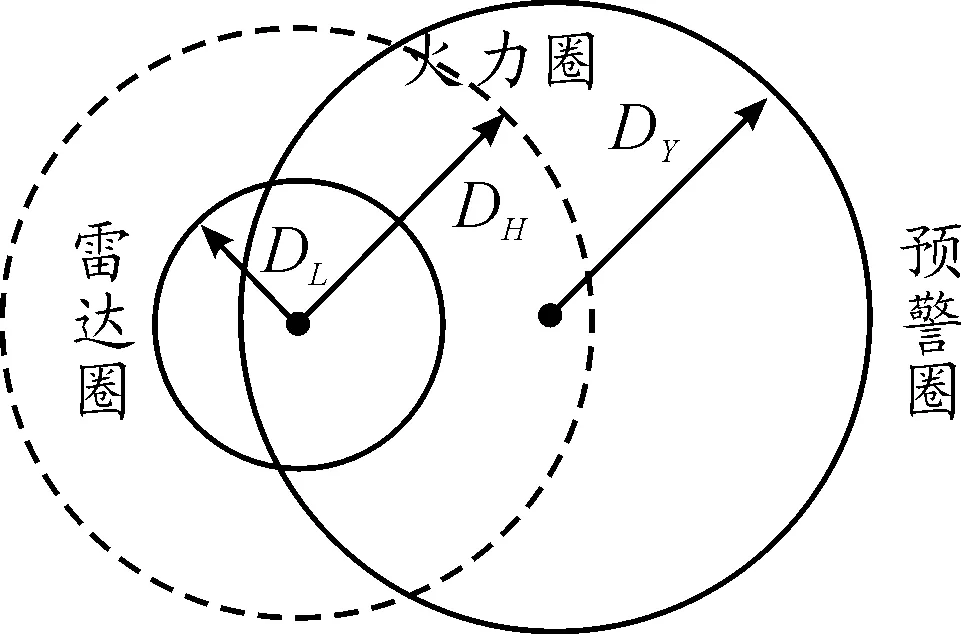
2.2 導彈最大飛行斜距
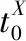
2.3 協同殺傷區遠界計算
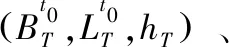
3 算例仿真

4 結論

