基于異質網絡的蜂擁控制研究
張金春,叢 凱,王帥磊
(海軍航空大學, 山東 煙臺 264001)
蜂擁行為是指蜂群、魚群、鳥群等生物群體利用簡單的幾條規則和環境信息,通過個體之間的相互影響,最終形成穩定有秩序的群體運動[1-7]。1987年,Reynolds[8]提出了具有代表性的蜂擁控制三條規則:分離、聚合和速度匹配。后來,Olfati-Saber[9]也對蜂擁控制算法改進和優化。現在,蜂擁控制已經在無線傳感器網絡、機器人編隊、無人機等各領域應用。1995年,Vicsek等[10]提出了均質感知模型:在二維平面上,存在一群初始位置隨機分布的質點,它們的運動速率相同但是運動方向隨機分布,并且感知半徑相同。因為質點的感知半徑相同,所以稱為均質感知模型。對于任意一個質點,它下一時刻的運動方向受到其感知半徑內其他質點的運動影響。
在實際生活中,很多智能體系統應該是異質的,即智能體的影響半徑各不相同。比如在生物群體中因為年齡和權威等個體差異使得每個個體對其他個體的影響能力各不相同。近年關于異質多智能體的研究中,文獻[11]在“跟隨者-領導者”的框架下,分別針對有外界干擾和存在多個虛擬領導者的情況,在異質多智能體系統中研究如何設計不同的控制策略使跟隨者能夠很好地跟蹤領導者。文獻[12]研究了異質多智能體系統的分組一致性,推導出了異質多智能體系統實現分組一致性的充分條件。文獻[13]研究了混合類型多智能體組成的異質多智能體系統的組一致性問題,得出了通信延遲與分組一致性無關的結論。本文主要研究當智能體系統異質時,異質性的強弱對于多智能體系統最終蜂擁狀態的影響。
1 蜂擁控制
1.1 預備知識
在二維平面上,假設存在n個智能體,全部視為質點。第i個智能體的運動方程為:
(1)
其中:qi∈Rn為第i個智能體的位置;pi∈Rn為速度;ui∈Rn為加速度,也就是控制輸入。
對于智能體i,在任意時刻t,將它感知半徑內的所有智能體的集合記為Ni(t)={j|||qi-qj||≤r2,j∈N且j≠i},其中,||·||為歐幾里得范數,r為感知半徑,稱Ni(t)為智能體i的鄰居。把智能體i視為節點,將它與其他能感知到的節點用無向邊連接,則由系統內所有節點和無向邊組成的網絡構成了一個無向圖G(t)。其鄰接矩陣為A(G(t))=[aij(t)],其中
(2)
冪律分布最早由Zipf發現,他發現英文單詞的出現頻率與其序號的常數次冪存在反比關系:
P(r)=r-α
(3)
本研究中,智能體的影響半徑服從冪律分布。
1.2 傳統蜂擁控制模型
1986年,Reynolds[9]提出了一種蜂擁控制模型,并提出了三條規則:分離、聚合、速度匹配。根據Reynolds提出的模型,Olfati-Saber[10]提出了如下控制輸入算法:
(4)

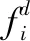
▽qiψα(|||qij-qγij||σ)
(5)

φα(z)=ρh(z/rα)·φ(z-dα)

(6)
控制輸入ui的具體形式為:
hi[c1(qγ-qi)+c2(pγ-pi)+uγ]
(7)
這里,hi可以用來描述智能體i是否擁有領導者的引導信息。當hi=1時,智能體i為信息智能體,當hi=0時,智能體為自由智能體。
人工勢函數ψα(z)滿足:① 當||qij||σ→0時,ψα為最大值;② 當||qij||σ趨近于某一期望值時,ψα為最小值;③ 當||qij||σ≥||r||σ時,ψα恒為很小的正常數。人工勢函數ψα如圖1所示。
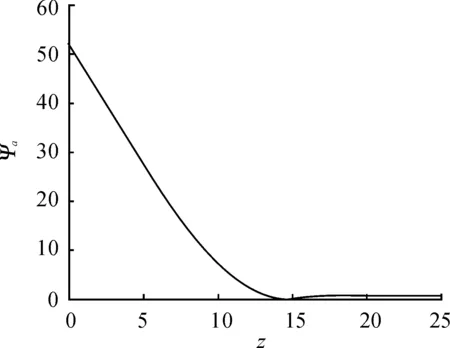
圖1 人工勢函數
1.3 影響半徑服從冪律分布的蜂擁控制算法
在Reynold和Olfati-Saber等提出的蜂擁控制算法中,ri表示的是智能體的感知半徑,即智能體i能夠感知到感知半徑ri內的其他鄰居的位置信息和速度信息,影響自己的控制輸入。但是在智能體系統異質時,感知半徑的概念無法表達智能體的影響能力,所以本文將ri重新定義為智能體i的影響半徑,即智能體i能夠將自己的位置信息和速度信息傳遞給影響半徑ri內的其他智能體。當智能體系統均質時,感知半徑和影響半徑的意義相同,但是當智能體系統異質時,感知半徑和影響半徑的不同會對結果產生不同的影響,所以要對控制輸入進行改造。
當智能體系統異質時,智能體i是否能夠接收到智能體j的信息取決于智能體j的影響半徑,所以新的鄰居定義如下:
且j≠i}
新的鄰接矩陣定義如下:
(8)
當智能體系統均質時,鄰接矩陣是對稱陣;當智能體系統異質時,因為影響半徑不相同,所以鄰接矩陣不是對稱陣。
除了鄰居和鄰接矩陣,異質網絡對于勢能函數也會產生影響。對于碰撞函數式(6),因為影響半徑不同,所以自變量應該替換為z/||rj||σ,而不是z/||r||σ。
最后,因為本文主要研究在異質網絡下多智能體系統的自主演化行為,所以本文不研究帶有領導者的蜂擁控制輸入,因為領導者具有全局信息,所以無論初始分布如何,最終肯定能夠形成穩定的蜂擁行為。在對鄰居、鄰接矩陣和碰撞函數進行改造以后,新的控制輸入如下:
其中,c3為系數,主要影響智能體之間的分離聚合作用,c3=0.25。

其中,xmin為系數,用以保證ri>d。
當冪律指數變化時,生成的智能體影響半徑分布也會發生變化。圖2是當s=55時不同冪律指數對應的影響半徑分布圖。

圖2 不同冪律指數下的影響半徑分布
2 仿真結果與分析
本研究模仿了50個智能體在二維平面中的運動情況。參數分別設置為:智能體初始速度為[-1,1]和[-1,1],初始分布范圍為[0,55]和[0,55],智能體最小影響半徑xmin=6,智能體間期望距離d=5,σ范數的參數ε=0.1,式(8)中參數h=0.9,φ(z)中a=1,b=2,控制輸入中c1=0.1,c2=0.9,c3=0.25,程序運行步數loop=300。為了更好地體現不同影響半徑下智能體之間的相互影響,本文不要求智能體的初始分布必須為初始連通。通過計算機數值仿真驗證當冪律系數分別等于γ1=4,γ2=5,γ3=7,γ4=10,γ5=50對智能體系統蜂擁狀態好壞和收斂速度的影響。
首先本文對γ1=4時的智能體系統進行了數值仿真,研究系統隨程序運行時的演化過程。
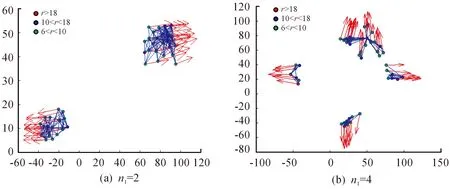
圖3(a)是智能體的初始分布圖。從圖中可以看出智能體的速度是隨機分布的,網絡的連通性也不強,其中有3個影響半徑r>18的智能體,因為影響半徑較大的原因,所以它們對其他智能體的運動有較強的引導作用,它們可以充當“中心智能體”的作用。當t=50時,可以看出所有影響半徑較小的智能體都受到幾個影響半徑較大的智能體的影響,向中心智能體運動。當t=100和t=150時,智能體已經基本完成了Reynolds提出的三條規則中的分離聚合作用,開始按照同一方向開始運動。當t=300時,所有智能體已經形成了穩定的α-晶格結構,并且在幾個中心智能體的影響下按照同一方向進行運動,形成了穩定的蜂擁狀態。
通過對上圖的分析可知,當冪律指數較小時,智能體系統中存在極少數影響半徑極大的智能體,它們可以充當“中心智能體”甚至“領導者”的作用,它們的速度和位置會對其他影響半徑較小的智能體產生決定性的作用,最終蜂擁狀態的好壞取決于極少數中心智能體的初始分布狀態。
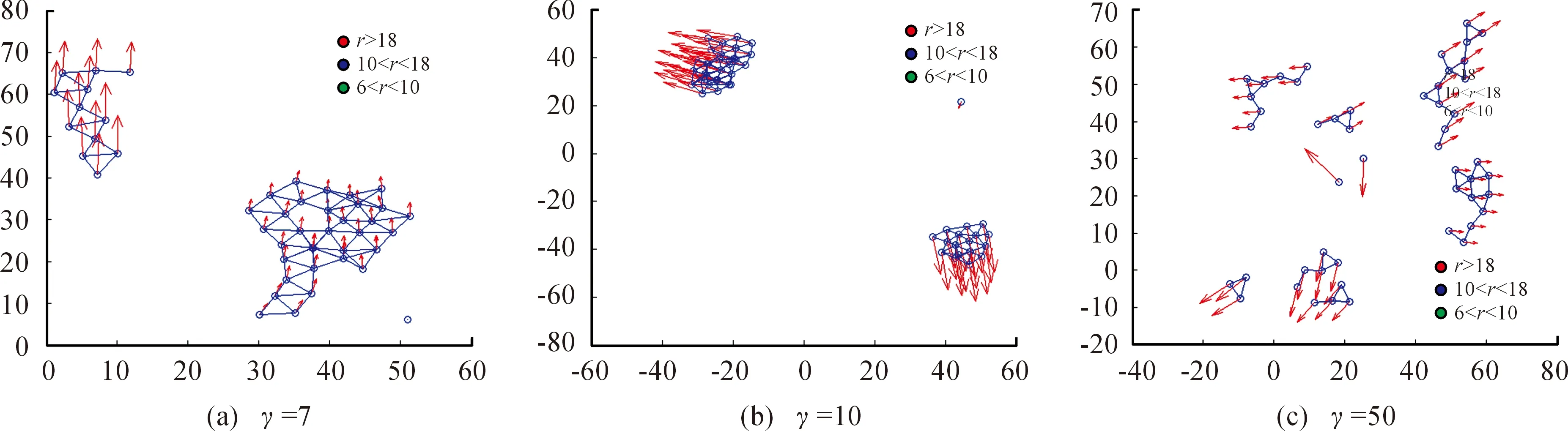
下面比較當冪律指數分別取γ1=4,γ2=5,γ3=7,γ4=10,γ5=50時對智能體系統的影響,每種情況分別取10次實驗數據取平均值。本文采用最大簇系數S來判斷蜂擁狀態的好壞,S為智能體節點網絡中所有連通子圖中最大連通子圖的智能體個數與所有智能體個數的比值,0 從圖4可以看出,當冪律指數較小時,智能體系統的初始最大簇系數比較大,這是因為系統中存在少數中心智能體,以這些中心智能體為節點更容易形成連通網絡;相反當冪律指數較小時,所有智能體的影響半徑都比較小,所以很難形成節點很多的連通網絡。 隨著程序運行,可以看出冪律指數較小的最大簇系數增長更快,這是因為中心智能體影響半徑更大,更容易影響其他智能體。并且可以明顯看出,冪律指數不同會對最后的最大簇系數產生很大的影響:當γ1=4,γ2=5,γ3=7,γ4=10,γ5=50時,s1=0.97,s2=0.844,s3=0.742,s4=0.624,s5=0.364。當冪律指數較小時,最大簇系數很大,收斂時間也更短,系統的蜂擁狀態也更好;當冪律指數較大時,最大簇系數很小,收斂時間更長。這說明當系統的異質性很強時,多數智能體在極少部分中心智能體的帶領下,更容易形成整體的蜂擁狀態;隨著異質性逐漸減弱,智能體變得更加均質,在運動過程中容易受到部分影響半徑較大的智能體的影響,形成“分塊”或者“分離”現象,如圖5所示。從圖5能夠看出,隨著異質性減弱,影響半徑越來越小,導致智能體的分離現象也更加明顯。 根據前面的數值仿真可知,當系統異質性很強時,智能體的運動主要受到極少部分中心智能體的影響,最終蜂擁狀態的好壞取決于中心智能體的運動狀態。接下來本文重點研究,在系統的異質性很強的條件下,中心智能體的運動狀態對智能體系統運動的影響,以及能否通過對極少部分的中心智能體施加控制,達到對整個智能體系統進行控制,最終形成統一的蜂擁運動。為了保證系統的異質性,接下來研究的內容中冪律指數γ=4。 為了對智能體進行分類,本文設定影響半徑r>20的智能體稱為控制智能體,影響半徑6≤r≤20的智能體稱為一般智能體。在運動過程中,設控制智能體保持勻速直線運動,則對于控制智能體來說ui=0,對所有智能體來說,控制輸入為: 圖5 不同冪律指數對應的分離現象 圖6 n1=3時不同時刻智能體分布 通過上面分析可知,在異質性較強的智能體系統中,極少數影響半徑很大的控制智能體的運動狀態可以影響其他所有智能體的運動,當這些控制智能體的運動方向不相同時,會對其影響半徑之內的其他智能體產生影響,最終會形成穩定的分塊式的蜂擁運動,并且影響半徑越大,形成的分塊也越大。接下來本文研究能否通過控制極少數中心智能體,讓它們按照同一方向運動,進而達到控制所有智能體的運動,最終形成穩定的蜂擁運動。設所有影響半徑r>20的控制智能體的速度都為(1,1),控制輸入ui=0,則所有控制智能體都按照同一速度進行勻速直線運動。 從圖8可以看出,t=0時,智能體的初始分布比較散亂;t=100時,所有智能體都能達到同一運動方向;t=300時,能夠形成比較緊湊的α-晶體結構。這樣就說明了在異質性較強的智能體系統中,即使初始分布隨機性很強,但是通過控制極少數控制智能體按照同一方向運動,就可以牽制絕大多數其他智能體,最終形成穩定的蜂擁運動。 圖7 n1=2,4時形成的分塊式的蜂擁運動 圖8 同一方向運動時的智能體蜂擁運動圖 1) 本研究提出了基于異質網絡的蜂擁控制算法。 2) 對勢能函數進行了改造,并且通過數值仿真證明了異質性較強的智能體系統更容易達到蜂擁狀態,并且證明了可以通過控制極少數影響半徑較大的智能體控制整個智能體系統,使其達到預定的蜂擁狀態。
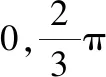

3 結論

