二元選擇分位數回歸模型的貝葉斯估計方法及模擬研究

邸俊鵬，張曉峒

（1.上海社會科學院 數量經濟研究中心，上海 200020；2.南開大學 數量經濟研究所，天津 300071）

0 引言

分位數回歸和貝葉斯估計屬于當前計量經濟學理論的前沿領域。分位數回歸作為一種不同于均值回歸、應用更廣泛、提供信息更豐富的計量方法，雖然早在1978年就被Koenker等[1]提出，但關于它的理論研究和應用研究方興未艾。貝葉斯估計尤其是采用馬爾科夫鏈蒙特卡羅（MCMC）方法，在小樣本性質、假設檢驗以及預測方面具有比傳統估計方法無可比擬的優勢，因而受到越來越多的關注。Yu和Moyeed[2]在2001年首次將貝葉斯分析方法應用于分位數回歸模型，提出貝葉斯分位數估計方法，并證實了該估計方法的有效性。

然而在貝葉斯分位數估計中大多數研究都是針對連續型因變量的，對離散型因變量，如二元變量的分位數回歸模型研究較少。目前離散型因變量模型代表性的文獻主要有：Manski（1975，1985）[3,4]定義了半參數的二元選擇分位數回歸估計量；Koenker和Hallock（2001）[5]主要致力于中位數上的二元選擇分位數回歸（Binary Quantile Regression）的相關研究；進而，Kordas（2006）[6]將該研究擴展到了各個分位數上，并闡明了二元數據的各分位數回歸可以提供解釋變量對因變量更豐富的影響。上述研究都是基于傳統的頻率學派方法的。Skouras（2003）[7]、Florios和Skouras（2008）[8]指出這些方法并不能保證得到目標函數的全局最優解。因此，采用頻率學派的方法求解二元選擇分位數回歸模型，無論在統計量的一致性方面還是在統計推斷方面都受到質疑。

本文將針對二元選擇分位數回歸模型的貝葉斯估計方法進行探索性研究。首先介紹基于ALD的貝葉斯二元選擇分位數回歸估計方法；進而通過模擬實驗，對不同先驗設定和不同抽樣算法下二元選擇分位數回歸估計量性質進行比較研究；最后，比較頻率學派方法和貝葉斯估計方法對二元選擇分位數模型進行估計時的不同表現。

1 二元選擇分位數回歸的貝葉斯估計方法

1.1 二元選擇分位數回歸

標準的二元選擇模型表達式為：

F（?）為累積分布函數。F（?）所采用的形式不同，二元選擇模型也相應不同，常用的二元選擇模型如表1所示：

表1 常用的二元選擇模型

因為線性概率模型不能保證條件概率的預測值在0和1之間，即使加以約束，其預測結果也往往與現實不符，故應用較少。Logit模型假設條件概率分布的累積分布函數；Probit模型假設條件概率為標準正態分布的累積分布函數；而對于互補對數模型，假設條件概率為極值分布的累積分布函數。Probit曲線和logit曲線都是在概率為0.5處存在拐點，但logit曲線在兩個分布的尾部要比Probit曲線厚。

其中，Q（?）和F（?）分別表示潛變量的條件分位數函數和條件分布函數，βτ為在τ分位數下的參數向量。因為潛變量是觀測不到的，所以不能直接用模型（2）進行估計。

為了估計離散選擇的分位數回歸模型，Powell（1986）[9]指出可以借助分位數回歸的同變性（Equivariance），這是分位數回歸的一大優勢。假設h（?）是因變量yi的變換（transition）函數，是定義在實數空間上的非遞減函數，那么對于任意的隨機變量y，則有：，即隨機變量先變換再進行分位數估計與先進行分位數估計再變換是等價的。因此隨機變量y的單調變換不影響分位數估計結果。在離散選擇模型中，潛變量與因變量yi之間滿足這種單調變換關系，因此潛變量與解釋變量的分位數估計結果可以通過可觀測的因變量與解釋變量的分位數估計得到。

1.2 頻率學派二元選擇分位數回歸方法存在的問題

頻率學派在估計二元選擇分位數模型時，首先要對其進行極大得分估計（maximum score estimate）。這個方法幾乎對誤差分布不作過多假設，只要求誤差以自變量為條件的中位數為0。因此，極大得分估計不知道解釋變量和誤差項的函數形式，因而它也適應存在異方差的情形。Manski（1975）[3]最早只是關注中位數上的估計，后來Manski（1985）[4]將其擴展到更一般的分位數情形。極大得分估計如下：

其中sgn（）為符號函數，ρτ（?）為損失函數。

Kim和Pollard（1990）[10]指出極大得分估計量收斂速度低而且漸近分布復雜，而極限分布的復雜性限制了它在統計推斷方面的應用，同時也使得目標函數不存在漸近的一階條件。Delgado等（2001）[11]采用子采樣（subsampling）的方法克服上述問題。他們從理論上證明了子采樣對于極大得分估計是有效的，并給出了模擬證據。但該方法的一個主要缺點是計算量大，因而它只適用于解決小樣本和維度低的情形。該方法起初用于中位數估計，Kordas（2006）[6]將其擴展到一般的分位數情形，但是這個平滑的估計量對誤差分布假設過于嚴格。模擬實驗表明，即使樣本容量很大時，用正態分布近似也是不準確的；即使采用自舉也很難得到估計量的標準誤差[12]。Skouras（2003）[7]、Florios和Skouras（2008）[8]則側重于就對目標函數（3）的優化，但他們指出沒有哪個算法可以保證能得到全局最優解，即使是采用改進的算法，如混合整數規劃（mixed integer programs）。總之，采用頻率學派的方法求解二元選擇分位數回歸，無論在統計量的一致性方面還是在統計推斷方面都受到質疑，即使提出了改進的方法，仍存在某些缺陷。

1.3 基于ALD的貝葉斯二元選擇分位數回歸估計方法

τ為關注的分位數，如τ=0.5，則是二元選擇中位數回歸。同樣地：

這里，Fy*（?）設定為非對稱拉普拉斯變量y*的累積分布函數。

π（β）為回歸系數的先驗分布，I（?）為指示函數。這個后驗分布不是我們所熟悉的分布，不可能對其進行直接抽樣，而MCMC方法可以解決這個問題。以β為條件的y*的全條件后驗分布是可知的：

當yi=1時，

當yi=0 時，

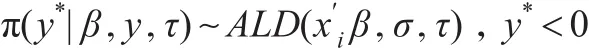
由（5）可知，以y*、τ和觀測值為條件的β的后驗分布是：

這個全條件后驗分布不同于潛變量y*的全條件后驗分布，不存在解析形式，因此采用MCMC方法，如Gibbs抽樣、M-H抽樣來獲取后驗分布。具體而言，給定觀測值、參數的先驗分布和感興趣的分位點，借助式（4）和（5）給出的條件分布，采用Gibbs或者M-H抽樣，可以得到聯合后驗分布（6）。以極大似然估計值為初值，并刪除開始的部分估計值，最后得到一個抽樣值序列，從而可以方便地得到參數的點估計和置信區間。這也是貝葉斯方法相對于頻率方法的一大優勢。

關于先驗分布，Yu和Moyeed（2001）[2]指出，回歸參數的先驗分布π（β）可以是任意的，即使是一個不合適的均勻分布，得到的后驗分布也是合適的。此外，由式（6）可知，后驗分布是由誤差服從非對稱拉普拉斯分布的假設所決定的，這也表明模型參數的估計量和統計推斷是受這個假設影響的。然而，在下文的模擬中可以看出，即使誤差不服從這個假設分布，相關結論也是相當穩定的。

1.4 模擬實驗

下面通過一個模式實驗展示采用貝葉斯方法分析二元選擇分位數回歸的過程。在二元離散選擇模型中，如果存在異方差，貝葉斯分位數回歸方法可以有效地捕捉和反應這種異方差。參數先驗采用模糊的標準正態分布，β～N（0,10），以此來減弱對后驗分布的影響。MCMC抽樣值的收斂性由從邊際分布中得到的抽樣值的時間序列是否平穩來判定。

首先通過下面的異方差模型，生成n=200數據：

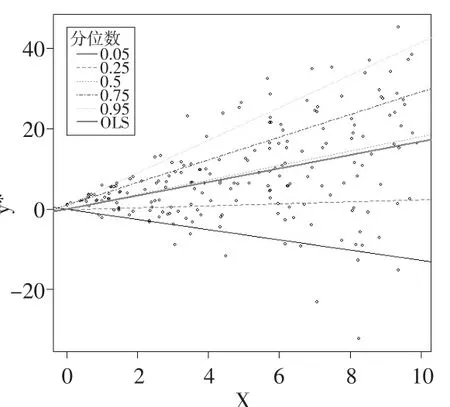
在上述數據生成過程（7）的基礎上，定義離散二元變量yi：當時yi=0，當時yi=1。采用貝葉斯二元選擇分位數回歸方法對其進行估計。由于為潛變量，是不可觀測的，所以本文使用的數據是二元離散變量yi和解釋變量x，來估計潛變量中隱含的異方差。在0.05、0.25、0.5、0.75、0.95分位數上的抽樣值軌跡圖和核密度圖如圖2所示。

比較使用二元選擇貝葉斯分位數回歸（圖2）和采用潛變量的貝葉斯分位數回歸得到的各分位數下估計值（圖1），見表2。

表2 貝葉斯二元選擇分位數估計量與真值的比較

圖2貝葉斯二元選擇分位數回歸系數的抽樣軌跡圖和核密度圖

表2中，β的真值與圖1中擬合直線的斜率相對應。從表2可以看出，通過可觀測的變量采用貝葉斯二元選擇分位數回歸方法得到的估計量雖然與真值在數值上有偏差，但是它仍可以反應各個分位數上潛變量與自變量的相關關系，比如在低分位數上負相關，且隨著分位數的提高，相關系數逐漸增大。在下文中比較不同抽樣方法對二元選擇分位數回歸估計結果時，采用某一分位數下的值占所有分位數下值之和的比例，來討論哪種抽樣方法更能反映各個分位數下變量之間的關系。

2 不同先驗設定下二元選擇分位數回歸估計量性質的比較

針對一般化的形式：

誤差項存在異方差。為比較不同先驗分布條件下估計量的差異，本文設定回歸系數的先驗分布為正態分布，而且隨著方差的減小，信息由弱到強。形式分別如下：

先驗設定1：β～N（0,100）

先驗設定2：β～N（0,10）

先驗設定3：β～N（0,1）σ為參數化的尺度變量，設定其先驗分布σ～χ2（3）。

根據上述數據生成過程，結合不同的先驗信息，運用Gibbs抽樣算法對模型參數進行估計，考察不同的先驗分布對估計結果的影響。

表3 不同先驗分布下二元選擇分位數回歸估計量分布的數字特征

由表3可知，與連續數據貝葉斯分位數回歸不同，二元選擇模型的貝葉斯分位數回歸參數在各個分位點下的偏誤和標準差均不受先驗分布的影響。因此，在對二元選擇模型進行貝葉斯分位數回歸時，不必考慮先驗分布的選取，即先驗可以是無信息先驗。

3 不同抽樣方法對二元選擇分位數回歸估計量的影響

在貝葉斯分析中，Gibbs抽樣和M-H抽樣是目前較流行的抽樣算法。而不同的抽樣方法施行不同的算法和抽樣規則，本文將比較采用Gibbs抽樣和M-H抽樣對二元選擇分位數回歸估計量的影響。

數據生成過程為：

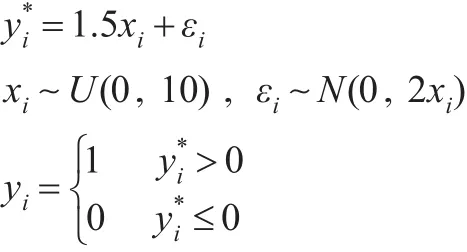
在Gibbs抽樣過程中，參數β的先驗分布為，將尺度變量σ參數化，并設定其先驗分布為χ2（3）。在M-H抽樣中，參數的先驗分布與Gibbs設定相同，建議分布為高斯分布。每種抽樣算法下共迭代6000次，為消除初值的影響，去掉前2000個抽樣值。通過抽樣值時序圖和自相關圖可以對兩種抽樣方法進行初步的比較。圖3是為樣本容量為200時，各分位數下Gibbs和M-H抽樣值軌跡圖和自相關圖。左列為Gibbs抽樣結果，右列為M-H抽樣結果；在每個分位數下，第一行為4000個抽樣值的時序軌跡圖，第二行為自相關圖。

圖3各分位數下Gibbs和M-H抽樣值軌跡圖和自相關圖

從0.05、0.25和0.5分位數的時序軌跡圖可以看出，兩種抽樣方法得到的馬爾科夫鏈都收斂，但Gibbs抽樣值的分布呈左偏形態，比較而言M-H抽樣值的分布較為對稱。從自相關圖角度看，Gibbs抽樣值的自相關度下降快于M-H抽樣值的自相關度。如在0.05分位數下，Gibbs抽樣值的自相關度在滯后10期時基本趨于零，而M-H抽樣值的自相關度在滯后35期才趨于零。在高分位數0.75和0.95下，抽樣結果表明Gibbs抽樣明顯優于M-H抽樣：Gibbs抽樣值的時序圖集中在某一個穩定值上下波動，且自相關圖快速衰減，基本在5期滯后衰減為零；而M-H抽樣值從時序圖可以看出馬爾科夫鏈收斂性差，存在自相關。此外不衰減的自相關圖也說明了這一點。因此，從抽樣的時序圖和自相關圖可以直觀地初步判斷，在高分位下Gibbs抽樣明顯優于M-H抽樣，而在低分位數下需要進一步考察。下面對抽樣得到的后驗分布的統計特征進行進一步的分析。

依照上述數據生成過程分別生成25、75、100、200、500、800容量的樣本，并在每個樣本容量下分別進行Gibbs和M-H抽樣，抽樣結果見表4。

表4 不同抽樣算法下二元選擇分位數回歸結果比較

通過以上分析，得出相關結論：①關于標準差：在給定樣本容量下，各個分位數上，Gibbs抽樣得到的后驗分布的標準差均小于M-H的標準差。這表明在貝葉斯二元選擇分位數回歸中，采用Gibbs抽樣得到的估計量精度更高，統計推斷更準確。②關于偏誤：在兩種抽樣算法下，抽樣后驗分布的均值對真值的偏誤都比較大，其結果與表3類似（表中未列出），而且Gibbs的偏誤比M-H的偏誤更大。但需要強調的是，在二元離散選擇模型中，每個分位數上估計量偏誤的絕對值并不重要，重要的是各個分位數上估計量的相對值，因此在表4中本文給出了各個分位數下估計量的偏誤占所有分位數上估計量偏誤之和的比重（特定樣本容量下，第一行數值），同時計算真值在各個分位數下占所有分位數上真值之和的比重（特定樣本容量下，第二行數值）。如果采用某抽樣方法時各個分位數上參數估計量的偏誤占總偏誤的比重更接近于對真值所對應的比重，則該抽樣方法更優。如樣本容量為100下，Gibbs抽樣得到的β在0.05、0.25、0.5、0.75、0.95分位數上的偏誤占總偏誤的比重分別為-0.270、0.012、0.151、0.232、0.542；而M-H 抽樣得到的β在上述分位數上的偏誤占總偏誤的比重分別為-0.074、0.010、0.046、0.144、0.874；真值在各分位數上的偏誤占總偏誤的比重分別為-0.187、0.025、0.202、0.397、0.563，顯然Gibbs抽樣下偏誤的相對值與真值偏誤的相對值更接近。由此可知，貝葉斯二元選擇分位數回歸采用Gibbs抽樣方法得到的估計量更能描述潛變量與自變量關系的全貌。

4 不同估計方法對二元選擇分位數回歸估計量的影響

針對二元選擇分位數回歸頻率學派的主要方法是基于二次抽樣標準差的二元選擇分位數回歸方法[4]和基于漸近標準差的二元選擇分位數回歸方法[6]。下面比較了不同樣本容量下貝葉斯二元選擇分位數回歸方法Bayes（LAD）與頻率學派這兩種方法的參數統計性質。

數據生成過程為：

差）

在不同樣本容量下，比較兩種傳統二元分位數回歸于貝葉斯二元分位數回歸得到的估計結果，實驗結果見表5。

表5 不同估計方法下二元選擇分位數回歸估計量比較

主要結論為：①隨著樣本容量的增加，三種估計方法下估計量的偏誤、均方誤以及置信區間都減小。這表明可采用的數據越多，參數的估計量越趨向于真值，而且估計的不確定性越小。②貝葉斯二元選擇分位數回歸（Bayes（LAD）估計量比頻率學派得到的估計量擁有更小的偏誤、更小的均方誤和更精準的置信區間。③隨著樣本容量的增加，頻率方法和貝葉斯方法得到的二元選擇分位數回歸估計量的差異會減小；BRQ和sBRQ在大樣本下才能進行可靠的統計推斷；同時這也說明，在小樣本情形下，貝葉斯方法用于二元選擇分位數回歸估計效果更好。上述結果也驗證了Benoit等（2012）[13]、Abrevaya和 Huang（2005）[12]、Kottas和Krnjajic（2009）[14]得出的結論。

5 總結

本文對二元選擇貝葉斯分位數回歸方法進行了研究，模擬結果表明：二元選擇模型的貝葉斯分位數回歸參數在各個分位點下的偏誤和標準差均不受先驗分布的影響，因此在對二元選擇模型進行貝葉斯分位數回歸時，不必考慮先驗分布的選取。在進行二元選擇分位數模型的貝葉斯估計時，與M-H抽樣相比，采用Gibbs抽樣得到的估計量精度更高，統計推斷更準確，更能描述潛變量與自變量關系的全貌，而且在高分位下Gibbs抽樣的優勢更明顯。貝葉斯二元選擇分位數回歸估計量比頻率學派得到的估計量擁有更小的偏誤、更小的均方誤和更精準的置信區間，尤其是在小樣本情形下，采用貝葉斯方法對二元選擇分位數回歸模型進行估計效果更好。